Fattorini H.O., Kerber A. The Cauchy Problem

Подождите немного. Документ загружается.

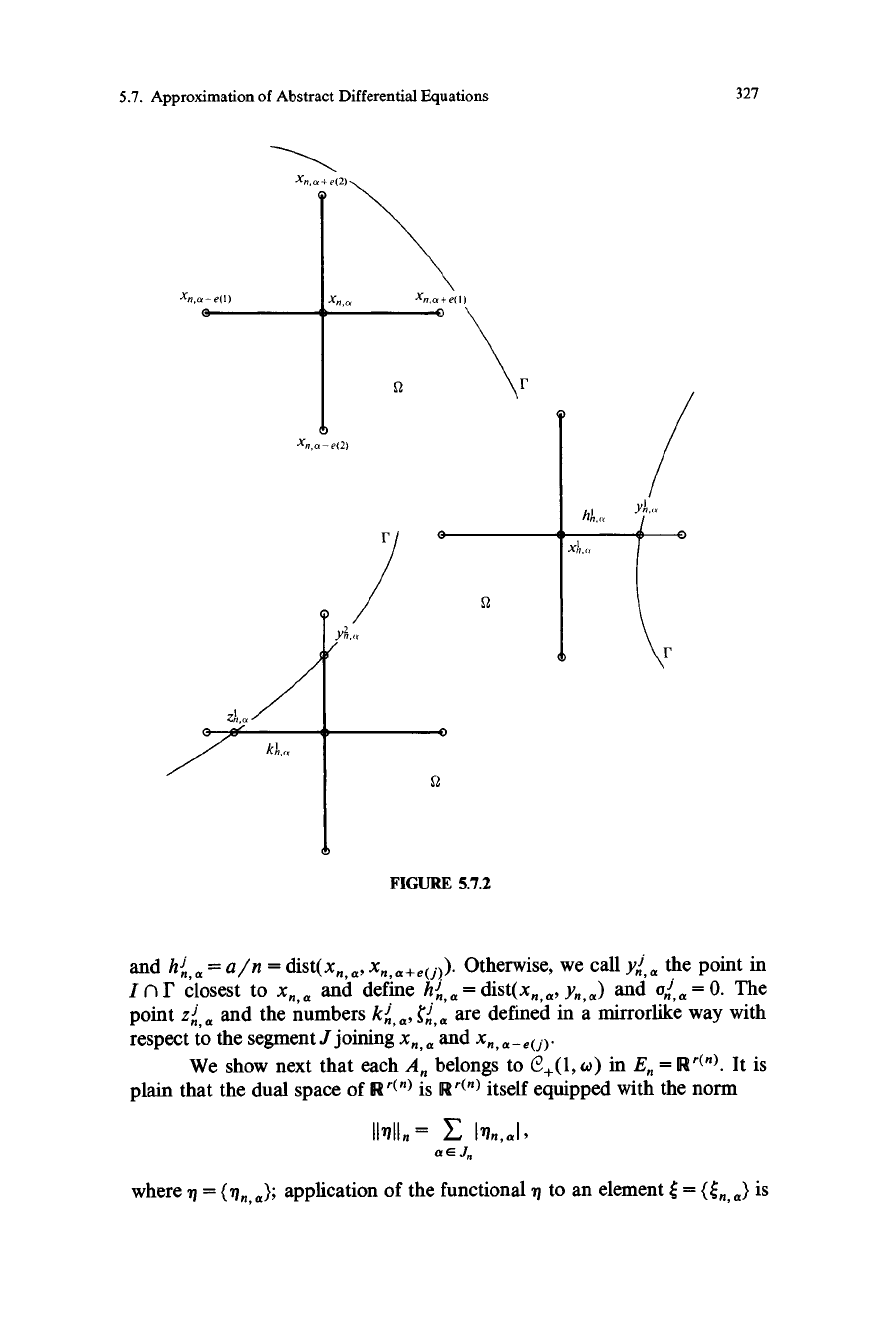
5.7. Approximation of Abstract Differential Equations

327

xn,a-e(U

xn,a + e(2)

x,,,a

xn,a-e(2)

FIGURE 5.7.2

}'n.a

tin.a

and hn,« = a/n = dist(xn,a, xn,a+e(j)) Otherwise, we call y4. the point in

I n 1' closest to xn,

and define hi,,

a =

dist(xn

a, Yn, a)

and on

, « =

0. The

point zn,

and the numbers ki,,

are defined in a mirrorlike way with

respect to the segment J joining xn,

and xn,

a - e(j )

We show next that each An belongs to C'+(1, w) in En = Rr(n)It is

plain that the dual space of R r(n) is O

r(n) itself equipped with the norm

117111n= Y- 171n,.11

aEJn

where 71= (71n a); application of the functional 71 to an element _ (

n, a)

328

Perturbation and Approximation of Abstract Differential Equations

expressed by

aE n

The duality set O(ff) of any E En can be described as follows. Let

(a E Jn; IIEIIn). Then O(ff) consists of all q = (,In a) such

that E I nn,

I = III I In, Tin, = 0 for a 4 m

?I n, asn, , % 0 for all a.

Consider an arbitrary nonzero E R'(n) and let a E m(E). If Sn a > 0,

then

sn a

is a maximum of (fin a) and (An )n

< wI n,al <

on the

other hand, if

Sn a

< 0, we obtain arguing in the same way that (AnE)n,a

- w I n, a I ; in any case, if q E 0 (e) we have

(q, An) <

(E E

R`(n)(5.7.51)

thus proving that An E (2+(1, w; En).

To apply Theorem 5.7.11, we must identify d = ex-lim An. To this

end, we take u E C (2) (S2) n Cr (CZ) and compute AnPnu; to avoid notational

complications, we only do the calculation with (5.7.49). Using the Taylor

formula for{ f up to second order terms, we( see that

I Dh,kl (X)-J "(x)I <

"(X + a)- f"(x)I + If"(x)- f"(X - T)I,

where 0 < a < h, 0 < T < k, thus we easily verify that

IIAnPnu - PnAulln - 0. (5.7.52)

Since C(2)(Sl)n Cr(C2) is dense in Cr(SZ), we see that d= ex-lim An is

densely defined (thus single valued by Lemma 5.7.10) and

du=Au (u E C(2)(SZ)nCr(SZ)).

(5.7.53)

Let v be a smooth function (say, in 61. (S2)). Then if A is large enough, the

solution u E D(A) of

(XI-A)u=v (5.7.54)

belongs to all Hk(9) by Theorem 4.7.12, a fortiori to C(2)( C2) by Corollary

4.7.15. This fact, combined with (5.7.52), shows that

(XI -

e)(C(2)(C2)nCr(r2))

(XI -

A)(C(2)(S2)nCr(11))

is dense in E = Cr(C2). It follows that the assumptions of Theorem 5.7.11

are fulfilled and thus that 61 E e+(1, w; E). Moreover, it is a consequence of

(5.7.53) and following comments that,

if v E'5 (U), then R(X; CT' )v =

R(A; A)v so that R(A; C?) = R(A; A) (by denseness of 6D(Q) in C,(C2)), and

we deduce that

d = A.

(5.7.55)

We obtain from Theorem 5.7.11 that if

is an arbitrary solution of the

initial-value problem

u'(t) = Au(t),

u(0) = u, (5.7.56)

5.8. Approximation of Abstract Differential Equations by Finite Difference Equations

then

329

lim

IIexp(tAn)Pnu-Pnu(t)Iln=0 (5.7.57)

n- co

uniformly on compact subsets of t >, 0 (since u may not belong to D(A),

may be a generalized solution; see Section 1.2).

5.8. APPROXIMATION OF ABSTRACT

DIFFERENTIAL EQUATIONS BY

FINITE DIFFERENCE EQUATIONS.

A discrete semigroup with time scale T > 0 in a Banach space E is a

(E)-valued function C5 defined in the set (1T; 1= 0, 1, ...) (in other words, a

sequence of bounded operators ((25 (IT); 1= 0,1, ... )) with C5 (0) = I and

C ((l + M )T) = C5 (1T) C5 (mT) (1, m = 0,1, ... ). Obviously, we have

C5(lT)=CS' (l>, 0), (5.8.1)

where C = C (T); hence

(IT)il<Il(25

1It=eWIT

(1>_ 0) (5.8.2)

with c = T-' logIIC5I1

If {C5 (t); t>-O) is an arbitrary semigroup, then

(25 (IT); 1>, 0) is a discrete semigroup with time scale T. A theory of discrete

semigroups roughly parallel to that of uniformly continuous semigroups

(but much simpler in nature) can be easily developed. The generator of

(C5 (IT); l >, 0) is by definition

A =

C5(T)-I)

(5.8.3)

and we can express C5

from A by means of the formula

C5(IT)=(TA+I)'

(l>, 0).

(5.8.4)

Conversely, each bounded operator A is the generator of a discrete semi-

group C5 with time scale T;

it suffices to take formula (5.8.4) as the

definition Of S (IT).

There is a close relation between (C5 (IT)) and the uniformly continu-

ous semigroup (S(t)) defined by S(t) = e`A. To avoid inessential difficulties,

we shall assume from now on that the operators C5 (IT) are uniformly

bounded.

5.8.1 Lemma. (a) Assume

II(25(IT)II<C

(1>-0).

(5.8.5)

Then

IIS(t)II<C

(t,0) (5.8.6)

330

and

so that

=e `lT

(5.8.8)

m=0

<Ce `/T

(tmTi)m =C.

(5.8.9)

m=0

Taking 1= 0, (5.8.6) follows.

Since C5 and S obviously commute,

1- 1

`G' ((1-

On the other hand,

S(T)-CS(T)=S(T)-I-TA=

T(T-t)A2S(t)dt

so that, if 0 < j < I - 1,

CS((1- j - 1) T) S(jT)((25 (T)-S(T))u

= ft(T-t)CS((1- j-1)T)S(7T+t)A2udt.

Making use of (5.8.9), we obtain

((I- j-l)T)S(jT)((25 (T)-S(T))ull <

zT2IlA2ull,

whence (5.8.7) follows immediately.

It is sometimes convenient to extend 5 to all values of t by defining

CS (t) = C (IT) in the interval [1T, (1 + 1) T); in other words, we set

CS(t)=CS([t/T]T)

(ti0),

(5.8.10)

where [s] is the greatest integer < s. Then

<III([t/T]T)u-S([t/T]T)uII+IIS([t/T]T)u-S(t)II

1-Tt]T 2

11A 2UII+ CTjjAujj <CT(2IIA2uII+IlAull),

(5.8.11)

Perturbation and Approximation of Abstract Differential Equations

11 (25

(IT)-S(IT)II <

2IT2

IIA2u11.

(5.8.7)

Proof. Noting that tA= (t/T)C5(T)-(t/T)I, we have

C5(1T)S(t)=e-t/TCS(IT) E

M=O

5.8. Approximation of Abstract Differential Equations by Finite Difference Equations 331

where we have estimated in an obvious way the equality

S(t')u - S(t)u = ftt S(s)Auds.

We examine in this section the following situation. Let (En, Pn)

approximate E in the sense of Section 5.7 and let A E C'+(E). A discrete

semigroup { C25

(l Tn )) with time scale Tn - 0 is given in each En, and we seek

to approximate S by the C25 n in the following sense:

I)(25n(InTn)Pnu-PnS(t)u11n- 0,

(5.8.12)

where (In) is a sequence of nonnegative integers such that

lnTn 9 t.

Each of the results in Section 5.7 has an exact counterpart for discrete

semigroups in relation with the present definition of approximation. We

begin with that of Theorem 5.7.5; here and afterwards (Tn) is a sequence of

positive numbers tending to zero.

5.8.2

Theorem. Let A E (2+(C,0; E), An E (En), {C25n(ITn);

1 > 0)

the discrete semigroup with time scale Tn -* 0 generated by An. Let, moreover,

Ii(25n(ITn)Il'<C

(l,0,n,l)

(5.8.13)

for some C not depending on n. (a) Assume that for each u E E

II'25n([t/Tn]Tn)Pnu-PnS(t)ulln-*0 (5.8.14)

uniformly on compacts of t > 0, where [s] = greatest integer < s and S, (t) _

exp(tA). Then

IIR(A; An)Pnu - PnR(A; A)uII

-* 0

(5.8.15)

uniformly on compact subsets of Re A > 0. (b) Conversely, assume that (5.8.15)

holds for some A with Re A > 0. Then (5.8.14) holds uniformly on compact

subsets of t > 0.

Proof.

If A > 0,

R(X; An)

(XI-

An)-1

(

=(x1-Tn

= Tn((ATn + 1)1 -

=Tn

(ATn+1)-(1+1)(25n(lTn).

(5.8.16)

t=0

Observe that the sum on the right-hand side of (5.8.16) is nothing but the

integral in t > 0 of the function

(5.8.17)

332 Perturbation and Approximation of Abstract Differential Equations

Now, since (1 + z/n)-n -

e-2

as n -* oo uniformly on compacts, it follows

that for each to, 8 > 0,

(I+ATn)-[t/Tn]-1-e-xt

(5.8.18)

uniformly on compact subsets of Re X >, to, t >, 8. Note next that if x >, 0,

then (l+x)",I+ax+Za(a-I)x2,1+ax+-4'«2x2 for a, 2. Accord-

ingly, if Re X >, to,

(I+ATn

)[tITn]+I >

(I+WTn

)[t"Tn]+I

(1+WTn)U/Tn)

+ wt + 4WZt2 (5.8.19)

for t >, 8 and n sufficiently large. Collecting these observations, we deduce

from (5.8.14) that

IIF,,(t,X)Pnu-Pne-"'S(t)IIn- 0

(5.8.20)

uniformly on compacts of Re X > to for t >, 8, while in view of (5.8.19),

IIFn(t,X)Pnu-P,,e-'LtS(t)ullnl<a(t) (t,0) (5.8.21)

with summable in t > 0. Integrating,

IIR(X;

An)Pnu- P,,R(X; A)ulln< f°IIF(t; \)Pnu -Pne-aS(t)ullndt,

(5.8.22)

and the proof of (5.8.15) ends by division of the interval of integration and

application of the dominated convergence theorem.

To prove (b) we begin by using Lemma 5.8.1 to deduce that the

semigroups (S,,(t)) = (et An) satisfy

IIS,,(t)IInSC

(5.8.23)

and apply Theorem 5.7.5(b) to show that

IISn(t)Pnu-Pns(t)Ulln- 0 (5.8.24)

uniformly on compacts of t >, 0. We make then use of (5.8.11) for each Can

and S,,; ifReX>0,

II((2 n([ t/Tn1 T,,

S,, (t)) R(X; An

)211"

CT,,(2IIA2R(X; AU)2IIn+IIAnR(X;

A,, )2IIn).

(5.8.25)

Since A,, R (X; An) = X R (X; An) - I is uniformly bounded in norm, the

right-hand side of (5.8.25) tends to zero uniformly on compacts of t > 0.

Select now u = R(X; A)2v in D(A2). Then

Pnu = P,,R(X; A)2v

=R(X; An)2Pnv+(P,,R(X; A)2v-R(X; A,, )2Pnv). (5.8.26)

5.8. Approximation of Abstract Differential Equations by Finite Difference Equations 333

Reasoning as

in the

proof of Lemma 5.7.7,

we can show that

IIP,,R(A; A)2v - R(A; An)2Pnvlln - 0. Combining this with (5.8.23) and

(5.8.24), we obtain (5.8.14) for u E D(A2), thus for u E E by uniform

boundedness of 5n and S.

The following result is an analogue of Theorem 5.7.6.

5.8.3

Theorem.

Let (C5

(l Tn ); I> 0) be a discrete semigroup in En

with time scale Tn -* 0 and generator An. Assume that

II(25n(lTn)II < C (1 > 0, n > 1)

(5.8.27)

with C independent of n. Suppose there exists some A with Re A > 0 such that

for each uEEthere is avEE Ewith

IIR(A;A,,)Pnu-Pnvlln-*0.

(5.8.28)

Assume, moreover, that

lim IIAR(A; An)Pnu - Pnull

n =

0 (5.8.29)

for each u E E uniformly with respect to n. Then there exists A E (2+(C,0; E)

such that (5.8.15) holds; a fortiori (5.8.14) is satisfied uniformly on com-

pacts of t > 0.

Proof. Making use of Lemma 5.8.1 we deduce that

IIS,,(t)IIn'<C

(t>0), (5.8.30)

hence Theorem 5.7.6 can be applied to show the existence of A and the

relation

II SS(t)Pnu -

-* 0

(5.8.31)

uniformly on compacts of t > 0. The corresponding relation for the C n

then derived as in the end of the proof of Theorem 5.8.2.

Finally, we prove a counterpart of Theorem 5.7.11.

5.8.4

Theorem.

Let (C5 n(1Tn ); 1 > 0) be a discrete semigroup in En

with time scale Tn - 0 and generator An such that (5.8.27) holds. (a) Assume

that C? = ex-lim An is densely defined in E and that (AI - &)D(l) is dense in

E for some A > 0. Then d E e+(C,0; E) and for each u E E,

Sn(It/Tn]T,,)U - S(t)U (5.8.32)

uniformly on compact subsets of t > 0, where S(t) = exp(ta ). (b) Conversely,

if C5n([t/Tn]Tn) converges strongly, uniformly on compact subsets oft > 0 to a

strongly continuous semigroup

with

IIS(t)II<C

(t>0), (5.8.33)

then d = ex-lim An is single valued and coincides with the infinitesimal genera-

tor Of S(.).

The proof of (a) follows again from application of Theorem 5.7.11 to

the An (Lemma 5.8.1 implies that IISn(t)II < C) whereby (5.8.24) results; the

334

Perturbation and Approximation of Abstract Differential Equations

proof is then ended as that of Theorem 5.8.2. To show (b), let A be

the infinitesimal generator of S, u E D(A), v = (Al - A)u for Re X > 0

and un = R(X; An)Pnv. We make then use of (5.8.22) instead of (5.7.43) to

show that

Ilun - Pnull

- 0;

since Au = Au - v and Aun = Xun - Pnv,

II Anun - P,,AuII

X Ilun - Pnull

-* O, hence u E D(6,) and du=Au. The

proof is completed like that of Theorem 5.7.11.

5.8.5

Example.

Finite difference methods for a parabolic equation. We

apply the results to the operator A in (5.7.45), using the notations and

definitions in the previous section. The operators An are defined in (5.7.50);

we replace the semigroups (Sn(t)) = (e",,) by the discrete semigroups with

time scale Tn generated by An, that is, by the C5n defined by

C5n(lTn)=(THAW+I)'.

(5.8.34)

This amounts to replacing the differential equation u;, (t) = Anu(t) by the

difference equation

Tn '(un(t + Tn)- un(t)) = Au(t) or, equivalently,

un(t + Tn) = (THAW + I)un(t). It is also obvious that condition (5.8.27) for

the discrete semigroups C5 n

will be satisfied if and only if we can select the

time scales Tn

0 in such a way that

ll(TnAn+I)`lI <C (l>0,n,1).

(5.8.35)

_ (i;n a) E En = Rr(n), we have

2Tn

((T,,An+I) )n,a=

(hj

+ kj

)

(kn

j=1

n,a n,a n,a n,a

(1_2;

m 1

+;c(xn a))

Sn,a

(5.8.36)

j=' hn,akn,a

Hence

)iiII(TA+ I

)EIIln

j=1 hn,akn,a

m 1

+(1-2Tn

+TnC(xn a)

I1 IIn

j=1

n,akjn,a

IIlln

(5.8.37)

for n large enough if

c(x)

; 0

(5.8.38)

and

Tn<4( j

) (n,1).

(5.8.39)

j=i hn,akn,a

5.8. Approximation of Abstract Differential Equations by Finite Difference Equations 335

Obviously (5.8.37) implies (5.8.35). The fact that t = ex-lim An = A was

already shown in Example 5.7.12, and it follows then from Theorem 5.8.4(a)

that if u(.) is an arbitrary (genuine or generalized) solution of (5.7.56), then

lim II

`G' n(Lt/Tn1Tn)Pnu - Pnu(t)II

n ->oo

lim II(T,,A,, +I)"IT-'Pnu-Pnu(t)IIn=0

(5.8.40)

n- oo

uniformly on compact subsets of t >, 0 if condition (5.8.39) on the Tn holds

for all n.

Inequality (5.8.39) is rather restrictive since very small h,;,

a, kn,

may

appear for any n. Even if this can be avoided due to the geometry of the

boundary F, (5.8.39) implies

Tn<1

(a)z

(n>, 1),

(5.8.41)

which forces us to choose time scales Tn much smaller than a/n, the "space

scale," and makes then necessary the computation of very high powers of

TnAn + I. One way out of this difficulty is to approximate (5.7.56) by the

implicit finite difference equation Tn'(u(t + Tn)- u(t)) = Anu(t + Tn), or, in

explicit form, u(t + Tn) =(I - which corresponds to the dis-

crete semigroup

tn(ITn)_(I-TnAn)_'

(l>,0)

(5.8.42)

with generator

An = Tn '((I - TnAn) -'-I)

_ (I - TnAn)-'An. (5.8.43)

The existence of the inverse of I - T,,An is assured since each An is dissipa-

tive; precisely, we have

tt t

r t

11(1- TnAn)SIIniII IIn

(5.8.44)

hence I I(I - TnAn) ' I I

< I and t n satisfies (5.8.27) with no conditions on the

time scales T

However, we must also check that

A = ex-lim An. (5.8.45)

To do this we select u E 044(S2)n Cr(S2) with Au E Cr(S2) and write

AnPnu - PnAu = (I - TnAn)I AnPnu - (I - T,, An)PnAu)

= (I - TnAn)-(AnPnu - PnAu + T,,AnP,,Au)

(5.8.46)

It was already proved in Example 5.7.12 that IIAnPnu - PnAuII

- 0 (under

the only assumption that u E C(z) (S2) n Cr (S2 )). The same argument applied

336

Perturbation and Approximation of Abstract Differential Equations

to Au shows that

II A,,

-0, hence

remains

bounded as n - oo so that II T,,A,,P,,Aull

-* 0 as Tn -* 0, and it follows from

(5.8.46) that

(5.8.47)

as n -p oo. It results again from Theorem 4.7.12 and Corollary 4.7.15 that

the solution u of (Al - A)u = v E 6D(2) belongs to C(4)(S2)n Cr(S2); more-

over, Au = A u - v E Cr (F2), thus we deduce from (5.8.46) that (9' , u = Au.

Arguing as in Example 5.7.12, we conclude that A = ex-lim An as claimed.

We obtain from Theorem 5.8.4 that

lim

II(I-T,,A,,)-[t/T"]Pnu-Pnu(t)IIn-+0

(5.8.48)

n -+oo

uniformly on compacts of t >, 0 under the only condition that T. -* 0; note

that although (5.8.39) assumes more of the T, (5.8.48) requires inversion of

the matrix (I - TnAn).

5.9. MISCELLANEOUS COMMENTS

Theorem 5.1.1 proved by Phillips [1955: 1] in a more general version.

Theorem 5.1.2 was also proved by Phillips [1953: 1]. The neutron transport

equation lends itself admirably to application of the theory of abstract

differential equations. For space dimension one, this was done by Lehner

and Wing [1956: 11; the treatment in arbitrary dimension is due to Jorgens

[1958: 1]. Many expositions in the same style and new results have been

subsequently published (see for instance Vidav [1968: 1], [1970: 1], K. W.

Reed [1965: 11, [1966: 11, Di Blasio 11973: 11 and Larsen [1975: 11. Some

details of the present treatment in spaces of continuous functions seem to be

new.

Theorem 5.3.1 has a long history. It was proved by Trotter [1959: 1]

for an unspecified sufficiently small a (but with additional information on

S(t; A + P); see (a) below), extended by Nelson [1964: 1] to the range a < 1

and by Gustafson [1966: 1] to a <1. We have followed Goldstein [1970: 51

in the proof. Corollary 5.3.2 is due to Chernoff [1972: 21 and independently

to Okazawa [1971: 11 in the particular case where E is reflexive (where

denseness of D(P*) is automatically verified; see Section 4). Perturbation

theorems for self adjoint operators are of earlier date: Corollary 5.3.5 is due

to Rellich [1939: 11 for the case a < 1 and A self-adjoint and was proved by

Kato [1951: 1] under the assumption that

IIPu112 < IIAu112 + b1Iu1I2

(u (=- D(A))

(5.9.1)

for some b >, 0. We note that, since (a + /3)'/2 < al/2 + #1/2, (5.9.1) implies

(5.3.14) with a = 1. The opposite implication is false: however, if (5.3.14) is

satisfied, we deduce that

IIPuI12 < a2IIAu112 + 2abII AuIIII ull + b211u112 <