Fattorini H.O., Kerber A. The Cauchy Problem
Подождите немного. Документ загружается.


2. 1. The Cauchy Problem in t > 0 67
FIGURE 2.1.1
0 < s < (n -1)t/n, decreases in (n -1)t/n < s < oo, and we obtain from
Stirling's formula that
= s
(tel s1`)n(1+o(1)) asn-oo. (2.1.18)
S
In view of this asymptotic relation, of the preceding comments and of the
inequality pe' -P < 1 which holds for p > 0, p 1, we obtain: if 0 < t' < t and
(n -1)/n > t'/t, then
yn(t,s)<yn(t,t')- 0 asn - oo (0<s<t') (2.1.19)
Let now k be an arbitrary positive constant. An elementary analysis shows
that the function eksyn(t, s) (n > kt) is decreasing in s > (n -1)t/(n - kt)
- t as n -' oo, thus if we select t" > t and make use again of the asymptotic
estimation (2.1.18), we obtain
ek`yn(t,s)-+ 0 asn -* oo (2.1.20)
uniformly in s > t".
We prove next that
u(t) = lim f
-Y" (t,
s)u(s) ds (2.1.21)
n -00 0
using the previous estimates for yn in a way familiar in the theory of

68
Properly Posed Cauchy Problems: General Theory
mollifiers. Let n > w't. Then
J
-f'Y,,(t,s)u(s)dsj < f
-
Yn(t,s)Ilu(t)-u(s)Iidt
0 0
= In
(2.1.22)
where the right-hand side of (2.1.22) corresponds to the division of the
domain of integration into the subdomains (0, t - 8),(t - S, t + 8),(t + 6, 00),
where 0 < S < t. Let e > 0. Taking S sufficiently small and availing ourselves
of the continuity of at t, we may assume that Il u(t)- u(s)II < e/3 for
t - S < s < t + S; in view of (2.1.17), this assures that I I J (S )I I < e/3 indepen-
dently of n. Once S has been chosen in this way, we use (2.1.19) and choose
n 0 so large that III(6)II < e/3 for n >, n 0. The third integral is similarly
treated, observing that by virtue of (2.1.14) and (2.1.20) with k = 2w' we
have
IIYn(t,s)u(s)II<C'pne-"s
(Sit+S),
where pn - 0 as n - oo. This completes the proof of (2.1.21).
We combine (2.1.21) with (2.1.16) to obtain
u(t)= lim (n)R(n)nu (t>0) (2.1.23)
t t
Making use of inequalities (2.1.11), we deduce that
Ilu(t)II <nliM
C(t)n(t
-
w) - nlIuII
= Ce"tIIuII
- 00
We define
(t > 0). (2.1.24)
S(t)u=u(t) (uED(A3),t>,0)
where u is the function in (2.1.12). Making use of arguments similar to those
employed in the treatment of S(.) (see Section 1.2), we show that S can be
extended to a (E)-valued strongly continuous function defined in t > 0,
satisfying S(0) = I and
I19(t)II <Ce"t
(t > 0), (2.1.25)
C, w the constants in (2.1.24) (and in the hypotheses of Theorem 2.1.1).
Clearly, the proof will be complete if we can establish that
u(t) = S(t)u(0) (2.1.26)
for all solutions of (2.1.1) (and not only for those originating in D(A3)
defined by (2.1.12)). In order to show (2.1.26), we observe first that it
follows immediately from the definition of S(t) that S( t) R (A) u =
R (A) S(t) u if u E D( A3 ); by the usual continuity argument, this equality
must then hold for all u E E. This implies that S(t)D(A) C D(A) and
S(t)Au=AS(t)u (uED(A),t>0).

2.1. The Cauchy Problem in t > 0
69
On the other hand, it is a simple consequence of (2.1.12) and the definition
of S that M(t) = S(t) R (X )3 is a continuously differentiable (E)-valued
function in t >_ 0 and that M'(t) = AM(t). Accordingly, if
is any
solution of (2.1.1) we have
d
dtM(t-s)u(s)=0 (0<s<t).
Then R(X)3u(t) = M(0)u(t) = M(t)u(0) = R(X)39(t)u(0), from which
(2.1.26) results since R(X)3 is one-to-one. This ends the proof of Theorem
2.1.1.
Note, incidentally, that although solutions of (2.1.1) are initially
defined only for initial data in D(A3), this is enough to establish that the
Cauchy problem for (2.1.1) is well posed and thus, by virtue of (2.1.9) and
preceding comments, solutions actually exist for arbitrary initial data in
D(A).
2.1.2 Remark. Formula (2.1.23) can be written in the following manner:
S(t)u= lim (I- tA) nu (t>O). (2.1.27)
noo
n
Strictly speaking we have proved this only for u E D(A3). However, it
follows from inequalities (2.1.11) that II(I-(t/n)A)-nII is bounded for
n > wt. Therefore (2.1.27) actually holds for all u E E (Theorem 1.1) and can
be used to justify writing
S(t) = e`A (t > 0). (2.1.28)
More results in this direction will be found later (see Section 2.5).
2.1.3 Example. Using the convergence arguments leading to (2.1.21) show
that the limit in (2.1.27) is uniform on compacts of t >_ 0.
2.1.4 Remark. In the sufficiency part of Theorem 2.1.1, inequalities
(2.1.11) need only be assumed for It real, µ > w. In fact, assume that R(µ)
exists for µ > w and
IIR(µ)YII < C(µ - w)- n
(,u> w, n i 1). (2.1.29)
Let tt > w. We know (Section 3) that if the series
00
E
(µ-X)'R(µ)'+1
(2.1.30)
j=0
converges in (E) for some complex A, then A E p(A) and (2.1.30) equals
R (X ). But, in view of (2.1.29) the series converges in (E) whenever I A
- µ I
< I µ - co I . Differentiating term by term and making use of formula (3.5),

70
Properly Posed Cauchy Problems: General Theory
we obtain
R(X)n - (- 1)n-I
R(X)(n-I)
(n -1)!
= 1 E
00
n+IR(µ)'+
(n-1)!
l=n-I
(2.1.31)
in
J X - µ I < I It - to 1. Replacing inequalities (2.1.29) into (2.1.31) we obtain
the following estimates:
n+I
IIR(X)nll
(nC1)'
.
E
00
I
j(J - 1)... (j - n +2) I(µ
_
),+I
(2.1.32)
Let next A be such that Re X > w. Take µ real and so large that the disk
I
- µ I < I
X
- µ I
entirely belongs to Re > w and let I AO = µ - I X - µ I
.
Since
I X - µ
µ - µo, we obtain, making use of (2.1.31) for A = co, that
IIR(X)nII S C(µo - w)
- n
(n
> 1).
(2.1.33)
We let now
+ oo and note that µo - Re X, thus obtaining inequalities
(2.1.11). Of course inequalities (2.1.29) need only be assumed for a sequence
µn-900.
Im X
ReX>w
w
I go =µ-IX-µI
Re X
FIGURE 2.1.2

2.2. The Cauchy Problem in - oo < t < oo. The Adjoint Equation 71
*2.1.5 Example (Phillips [1954: 1]).
Obviously, the first inequality (2.1.29) im-
plies all the others if C = 1, but if C > 1, not even the first inequality (2.1.11) implies
necessarily the others (see also Hille-Phillips [1957: 1, p. 3711).
2.1.6 Example.
Let A be a (not necessarily densely defined) operator
such that R(A) exists for large real A and satisfies the first inequality
(2.1.29). Then, if u E D A ,
lim AR(A)u=u.
X
00
(Hint:
Prove this first for u E D(A) and use Theorem 1.1.)
In all the following three examples, A is an operator satisfying the assump-
tions of Theorem 2.1.1.
2.1.7 Example.
D(A°°) = n' ID(A") is dense in E. (Hint:
Consider the set of
all elements of E of the form fcp(t)S(t)u dt, where u (-=E and q) is a test function
with support in t > 0.)
2.1.8 Example. If u E D(A), then
S(t)u-nE -Anu, (2.1.34)
=O
n
where " -" means "asymptotic in the sense of Poincare as t - 0"; precisely, we
have
n-1
j
lim
S ( t )
t A'u
= 1 Anu. (2.1.35)
t-o to
J=O fi nI
2.1.9
Example. (a) If u E D(A), w'> w,0 (w the constant in (2.1.3)), u E D(A),
then
S(t)u= lim
1
( +irex$R(X)udX
(2.1.36)
roo 2771 w'-ir
for t > 0, the limit being uniform on compact subsets of t > 0. For t = 0 the limit is
U.
(b) If u E E, w' > a), O and u E E, then
S(t)u= lim
I
IW
+ir(1_ _ImX )eXtR(X)udX
(2.1.37)
r -,oo 2i
r
in t > 0 with the same provisos as in (a). Note that this last integral can be
considered as the Cesaro limit of the integral in (2.1.36).
The two formulas should be compared with (1.2.14).
2.2. THE CAUCHY PROBLEM IN - oo < t < oo.
THE ADJOINT EQUATION.
We attempt in this section the characterization of those densely defined
operators A that make the Cauchy problem for the equation
u'(t) = Au(t)
(2.2.1)

72
Properly Posed Cauchy Problems: General Theory
well posed in - no < t < no in the sense of Section 1.5. This characterization
turns out to be entirely reducible to the results in the previous section. In
fact, we have
2.2.1 Theorem. Let A be closed. The Cauchy problem for (2.2.1) is
well posed in (- no, oo) and its propagator S satisfies
IIS(t)II <Ce'1t1
(-oo<t<oo)
(2.2.2)
if and only if a(A) is contained in the strip I Re A I < w and
IIR(A)nll<C(IReAI-w)-n
(IReXI>w,n>, 1).
(2.2.3)
Proof
Assume the Cauchy problem for (2.2.1) is well posed in
- no < t < no. Reasoning as in Theorem 2.1.1 we deduce that R(X) exists in
Re X > w and Re X < - w and (compare with (1.5.4))
R(X)u= f00 ex`S(t)udt (uEE,ReX>w), (2.2.4)
0
R(X)u=-
J 00
e"S(-t)udt (ueE,ReX<-w), (2.2.5)
0
whence inequalities (2.2.3) follow from repeated differentiation as inequali-
ties (2.1.11) follow from (2.1.4). Conversely, assume that the inequalities
hold. Then, since R(X; - A) _ - R(- A ; A) it follows from Theorem 2.1.1
that the Cauchy problem for (2.2.1) and for
u'(t) _ - Au(t) (2.2.6)
are both well posed in t >, 0. Let u e D(A), u+(.) (resp. the solution
of (2.2.1) (resp. (2.2.6)) with u+(0) = u (resp. u_(0) = u). Then
u(t)=
(u+(t)
(t>0)
u_(-t)
(t<0)
is a solution of (2.2.1) in - no < t < oo. On the other hand, if (u. ( - )) is a
sequence of solutions of (2.2.1) in - no < t < oo with un(0) - 0, we see by
applying the second part of the definition of well posed problem to
u+(t) = u(t) and u_(t) = u(- t) in t >, 0 that un(t) - 0 uniformly on
bounded subsets of (- no, oo). This ends the proof of Theorem 2.2.1.
We introduce some notations. If A is a densely defined operator in
E, we say that A E (2+(C, w) if the Cauchy problem for (2.1.1) is well posed
in t >, 0 and (2.1.3) holds. When knowledge of one or both constants is not
essential, we simply write A E e+(w) or A E (2+. It is plain from the com-
ments preceding inequality (2.1.3) that 3+(w) = U((2+(C, w); 1 < C < oo),
C'+ = U(C+(w); - no < w < oo). In the same fashion we say that A E C' (C, w)
when the Cauchy problem for (2.2.1) is well posed in - no < t < oo and
IIS(t)II<Ce01'1
(-oo<t<oo). (2.2.7)
It is clear from (2.1.3) applied to t - S(t) and to t - S(- t) that when-

2.2. The Cauchy Problem in - oo < t < oo. The Adjoint Equation
73
ever the Cauchy problem for (2.2.1) is well posed, there exist constants
C, w such that (2.2.7) holds (we do not attempt here to distinguish
between the exponential growth of
for t > 0 and for t < 0). The classes
3 (w), e are defined in the same way as the classes e+(w ), e, that is, e (w) _
U(e(C,w); 1<C<oo), e=U(e(w); 0<w<oo).
2.2.2 Example. Show that (2 (w) = 0 if w < 0.
The problem of deciding whether a given operator A belongs to e or
to (2+ is in general not too easy to solve by direct application of Theorems
2.1.1 or 2.2.1 since their hypotheses involve the verification of infinite sets of
inequalities for the resolvent operator R(X). The following result is useful
when the form of the solutions of
u'(t) = Au(t) (2.2.8)
can be guessed in advance.
2.2.3 Lemma. (a) Let be a weakly measurable (E )-valued
function defined in t > 0 such that
IIS(t)II <Ce" (t,0).
Let A be a closed, densely defined operator such that R(µ) exists for µ > w'
and assume that for every u E E, u* E E*
f'O e-`(u*,S(t)u)dt=(u*,R(µ)u) (.t>w,w'). (2.2.9)
Then A E (2+(C, w) and the propagator of (2.2.8) coincides with S(-)
(b) Let be a weakly measurable (E )-valued function defined in
- oo < t < oo and such that
IIS(t)II<Ce"1`'
(-oo<t<oo),
and let A be a closed, densely defined operator such that R(it) exists for µ real,
I µ I > w' and the equalities (2.2.9) and
f °°e-µ`(u*,S(-t)u)dt=-(u*,R(-µ)u) (µ>w,w) (2.2.10)
0
hold. Then A E (2 (C, w) and the propagator of (2.2.8) equals S(-)
Proof. It follows from (2.2.9) that
00
(u*,R(µ)"u)=
(n-1)!
f tn-le-µ'(u*,S(t)u)dt
(.t>w,w',n>,l)
0
whence we obtain the inequalities I <u*, R(µ)"u) I < CIIu*II IIuII(µ - w)-" for
µ > w, w' and n >, 1. In view of the arbitrariness of u and u*, inequalities
(2.1.29) result and Theorem 2.1.1 (as modified by Remark 2.1.4) applies to
show that A E C'+. If S is the propagator of (2.2.8), then comparing (2.1.10)
(for n=1) with (2.2.9) we find out that the functions (u*, u) and

74
Properly Posed Cauchy Problems: General Theory
( u*, 9(-)u> (u* E E, u E E) have the same Laplace transform, thus by a
well known uniqueness theorem they must coincide. This ends the proof of
(a). To prove (b) we only need to observe that it was a consequence of the
proof of Theorem 2.2.1 that A E e if and only if both A and - A belong to
(2+.
We examine some artificial-but illustrative-examples where
Lemma 2.2.3 can be used. Other applications of the theory will be seen in
the following chapters.
2.2.4 Example. Let E = Co(- oo, oo). Define
Au(x) = u'(x),
(2.2.11)
where D(A) consists of all u E E whose derivative exists and belongs to E.
Clearly D(A) is dense in E (any test function belongs to D(A)). To compute
R (X) we examine the differential equation
u'(x)- Au(x) = - v(x), (2.2.12)
where v E E. It is an elementary exercise to show that if Re A < 0, the only
solution of (2.2.12) that belongs to E is
x
R(A)v(x)=u(x)=-fe'X(X-v)v(y)dy (-oo<x<oo), (2.2.13)
and since it follows from (2.2.12) that u' E=- E, it is clear that u E D(A). For
Re A > 0, the formula is
R(X)v(x) = u(x) = f meA(X-v)v(y) dy. (2.2.14)
X
In both cases u depends continuously on v in the norm of E.
Let now be the family of operators in (E) defined by
S(t)u(x)=u(x+t) (-oo<x,t<oo).
(2.2.15)
It is plain that
is strongly continuous and also that IIS(t)II =1 for
- oo < t < oo. Moreover, if µ > 0,
(fcc
e-"'S(t) v dt)(x) = f 00e-`v(x + t) dt
f"Oeµ(X-v)v(Y)
dY
X
and a similar computation takes care of the case µ < 0. It follows then from
Lemma 2.2.3 that A E 3 (1, 0) and that is the propagator of (2.2.8).
2.2.5 Example.
The same analysis applies in the spaces E = Lp(- oo, oo),
15 p < oo. The operator A is defined by (2.2.11), but D(A) is now the set of all
u E E such that u' exists (in the sense of distributions) and belongs to E; equiva-
lently, D(A) consists of all absolutely continuous functions in E whose derivative
(which must exist almost everywhere) belongs to E. Formulas (2.2.13) and (2.2.14)

2.2. The Cauchy Problem in - oo < t < oo. The Adjoint Equation 75
make sense in this context (verification that u (-= E involves Young's theorem 8.1). It
is again true that A E C (1, 0) and that the propagator of (2.2.8) is given by the
formula (2.2.15). In each case (as well as in the one examined in Example 2.2.4),
a(A) coincides with the imaginary axis. The group is isometric in C°(-oo,oo)
and in LP(- oo, oo):
IIS(t)u11=11u11
(-o0<t<00).
(2.2.16)
2.2.6 Example. Let E = LP(- oo, 0),
1 < p < oo, and let A be again defined by
(2.2.11); now D(A) consists of all absolutely continuous u in E such that u' E-= E and
u(0) = 0. We examine the equation (2.2.12), extending v to - oo < x < oo by setting
v(x) = 0 for x > 0. If Re X > 0, formula (2.2.14) provides a solution satisfying
u(x) = 0 and this solution is unique; clearly, u r= D(A). Moreover, u depends
continuously on v in the L P norm so that u = R (X) v. Consider now the operator
valued function
S(t)u(x)=
l
u(x+t), x< - t
l 0, -t<x<0
For µ > 0, we have
(x<0,t>0). (2.2.17)
I
f00
e-""S(t)vdt)(x)= f xe_l"v(x+t)dt
v =
f°eµ(x-y)v(Y)
dy
x
almost everywhere in x (recall that integrals are computed in the LP norm), thus A
belongs to C2+(1,0) and
is the propagator of (2.2.8). Note that each S(t) is
isometric:
IIS(t)u11=11u11
(t>0)
(2.2.18)
although, unlike in Examples 2.2.4 and 2.2.5, S(t) is not invertible except for t = 0.
The same argument works in spaces of continuous functions, but we must incorpo-
rate the boundary condition u(0) = 0 in the definition of the space to achieve
denseness of the domain of A. Accordingly, we define E as the space of all
continuous functions in - oo < x < 0 such that u(0) = 0 and u(x) -> 0 as x -> - 00
and Au = u' with domain D(A) consisting of all u in E with u' in E. Again each
S(t) is an isometry.
I U
S(t)u(x)
-t
x
FIGURE 2.2.1
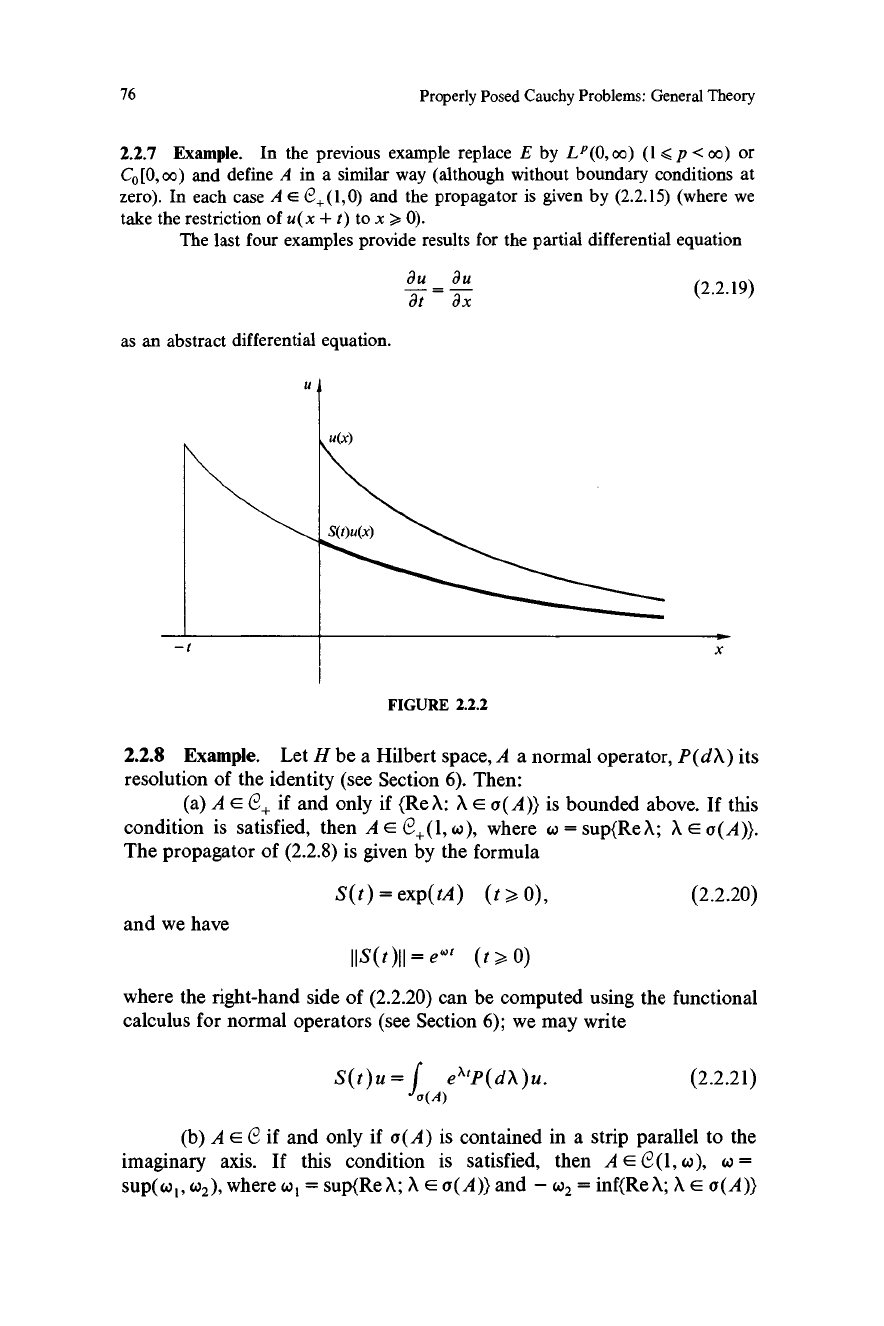
76
Properly Posed Cauchy Problems: General Theory
2.2.7 Example.
In the previous example replace E by LP(0,oo) (1<p<oo) or
CO[0, oo) and define A in a similar way (although without boundary conditions at
zero). In each case A E (2+(1,0) and the propagator is given by (2.2.15) (where we
take the restriction of u(x + t) to x > 0).
The last four examples provide results for the partial differential equation
du du
at
_
ax
as an abstract differential equation.
FIGURE 2.2.2
(2.2.19)
2.2.8 Example.
Let H be a Hilbert space, A a normal operator, P(dX) its
resolution of the identity (see Section 6). Then:
(a) A E ('+ if and only if (Re A: A E a(A)) is bounded above. If this
condition is satisfied, then A E (2+(1, w), where w = sup(Re A; A E a(A)).
The propagator of (2.2.8) is given by the formula
S(t)=exp(tA) (t>0),
(2.2.20)
and we have
IIS(t)II = e`
(t % 0)
where the right-hand side of (2.2.20) can be computed using the functional
calculus for normal operators (see Section 6); we may write
S(t)u= f eX`P(dA)u.
(2.2.21)
a(A)
(b) A E e if and only if a(A) is contained in a strip parallel to the
imaginary axis.
If
this condition is
satisfied, then A E (33(1, w), w =
sup((O i, w2), where wI = sup(Re X; A E a(A)) and - w2 = inf(Re X; A E a(A))
