Farin G. Curves and Surfaces for CAGD. A Practical Guide
Подождите немного. Документ загружается.


282 Chapter
15
Constructing Polynomial Patches
1
5.8
Shape Equations
The solution
to a
least squares problem
may be
close
to the
data points,
yet the
control
net
might "behave badly," similar
to the
curve case.
A way to
combat
such behavior
is to
invoke shape equations. These
are
conditions that
a
"good"
control
net
v^ould satisfy.
Out of
many possibilities,
we
choose
the
following:
a
translational surface
(see 15.3) is
characterized
by the
fact that
its
twist vanishes
everywhere.
For the
control
net,
this means
.
1,1]
K;
=
0;
/ =
0,..., m
- 1, / =
0,...,
w
- 1.
When
we add
these equations
to our
overdetermined linear system (15.17),
we
will
be
less faithful
to the
data points,
but
achieve
a
better shape
of the
control
net.
In
practice,
we
would weight
the
shape equations, maybe
by a
factor
of
0.1,
just
as we did for the
curve case.
1
5.9 A
Problem with Unstructured Data
The least squares approximation problem
for
Bezier patches leads
to an
interest-
ing question: what happens
if the
number
of
data points equals
the
number
of
unknowns.^
In
this case,
we do not
have
to
use
the
normal equations;
the
problem
directly yields
a
linear system with
a
square coefficient matrix.
Although this interpolation scenario appears simpler than
the
least squares
problem,
it has a
potential
for a
serious pitfall.
Our linear system
is
given
by
Po
LPKJ
B^{UQ)BI{VO)
.B^(UK)B-^{VK)
K(^O)B:(VO)
BZ(UK)B-{VK)^
rb,
'0,0
L
'^rn,n
-•
, (15.20)
but
now we
have
K = {m
-\-
l)(n
-\-1).
The assignment
of
parameter values
(^^,
Vj)
to the
data points
p/ is
(theoreti-
cally) arbitrary. We
now
perform
a
"thought experiment."^ Take
two
data points
PI
and
py.
They have parameters
(w^,
Vj)
and
(wy,
Vj),
Now,
leaving
the
data points
untouched, start changing their parameter values.
Do
this
as
follows: find
the
circle having (w/,
Vj)
and
(wy,
Vj)
as
diameter
and
move both (w/,
Vi)
and
(wy,
Vj)
3
Or
"Gedankenexperiment"
as
coined
by
A. Einstein.

15.10 Implementation 283
Figure 15.9 Unstructured data: two parameter locations
u^
=
(w^, Vj)
and
Uy
=
(wy, Vj)
are interchanged.
along this circle in a counterclockwise fashion until they have interchanged their
locations. Figure 15.9 illustrates.
The determinant of the linear system (15.20) has now changed its sign: two
of its rows are interchanged. It follows that somewhere during the interchanging
procedure, the determinant must have been zero, corresponding to an unsolvable
interpolation problem.
For an arbitrary collection of data point parameters, we cannot know if we
might be in or near an unsolvable situation. Hence this interpolation problem is
ill-posed.
15.10 Implementation
The following is the header for a program to plot a tensor product Bezier surface,
in fact, a rational one. If the polynomial case is desired, just set all weights to
unity.
void plot_ratsurf(bx,by,bw,degree_u,degree_v,u_points,v_points,
seale_x,seale_y)
/*
plots v_points isoparametric
curves
of the rat Bez
surface, each with u_points
points
on it.
Input:
bx, by:
arrays with
x- and y-
coordinates
of
control
net.
degree_u,degree_v: degrees
in u- and v-
direction
u_points,v_points: plot resolution
seale_x,seale_y: scale factor
for
postscript.
Output: postscript file

284 Chapter 15 Constructing Polynomial Patches
Next is a routine that fits a biHnearly blended Coons patch in between four
boundary control polygons, as described in Section 15.2. The routine works on
one coordinate only, and will have to be called separately for the x-, y-, and
^-components of a control net.
void netcoons(net,rows,columns)
/* Uses bilinear Coons blending to complete a control
net of which only the four boundary polygons are used as input.
Works for one coordinate only.
Input: net: control net.
rows,
columns: dimensions of net.
Output: net: the completed net, with the old boundaries.
*
/
15.11 Problems
1 Justify that in tensor product interpolation (Section 15.4), it does not
matter if we start with the row interpolation process or with the column
interpolation process. Give computation counts for both strategies. (In
general, they are not equal!)
2 Generalize Lagrange interpolation to the tensor product case.
* 3 Generalize quintic Hermite interpolation to the tensor product case.
* 4 Suppose we want to find a parametrization {ui) for a tensor product in-
terpolant. We may parametrize all rows of data points and then form the
averages of the parametrizations thus obtained. Or we could average all
rows of data points, for example, by setting p^ = ^-
^x^
y
and we could
then parametrize the
p^.
Do we get the same result? Discuss both methods.
PI Figure 7.3 shows how Lagrange interpolation behaves badly for curves.
Write a program to exhibit this effect for tensor product patches.

Composite
Surfaces
1 ensor product Bezier patches were under development in the early 1960s; at
about the same time, people started to think about piecewise surfaces. One of the
first publications was de Boor's work on bicubic splines [136] in 1962. Almost
simultaneously, and apparently unaware of de Boor's work, J. Ferguson [231]
implemented piecewise bicubics at Boeing. His method was used extensively,
although it had the serious flaw of using only zero corner twist vectors. An
excellent account of the early industrial use of piecewise bicubics is the article by
G. Peters
[462].
16.1 Smoothness and Subdivision
Let x(w, v) and y(w, v) be two patches, defined over [w/_i, uj] x [vj, Vj^i] and
[w/, w/+i] X [vj,
^'/+i],
respectively. They are r times continuously differentiable
across their common boundary curve x(wj, v) = y(w/, v) if all w-partials up to
order r agree there:
Z
dw
•x(u, v) (16.1)
u—ui
Now suppose both patches are given in Bezier form; let the control net of
the "left" patch be
{b^y};
0<i<m,0<j<n and those of the "right" patch be
{b^y};
m<i< Im^ 0 <j <n. We can then invoke (14.13) for the cross boundary
derivative of a Bezier patch. That formula is in local coordinates. To make the
transition to global coordinates (w, v), we must invoke the chain rule:
285

286 Chapter 16 Composite Surfaces
Figure 16.1 C^ continuous Bezier patches: the shown control points must be colHnear and all be in
the same ratio.
(xf^) E
A^'X-.^BJCt')
=
{£j i: ^'''K,iBy\ (16.2)
where Aj = wj^j
—
Wj.
Since the
B^Av)
are linearly independent, we may compare
coefficients:
This is the C^ condition for Bezier curves, applied to all « + 1 rows of the com-
posite Bezier net. We thus have the C^ condition for composite Bezier surfaces:
two adjacent patches are (J across their common boundary if and only if all rows
of their control net vertices can he interpreted as polygons ofC^ piecewise Bezier
curves. We have again succeeded in reducing a surface problem to several curve
problems. The smoothness conditions apply analogously to the t^-direction.
The basic theory for r = 1 is illustrated in Figure 16.1. An example of two
C^bicubic patches is shown in Figure 16.2.
The C^ condition states that for every;, the polygon formed by bo^y,...,
him^j
is the control polygon of a C^ piecewise Bezier curve. For this to be the case,
the three points b^_i
y,
b^y, b^_^i
y
must be collinear and in the same ratio
for all ;. Simple collinearity is not sufficient: composite surfaces that have
bm-l,/?^^,/,
bm+i,y collinear for each / but not in the same ratio will in gen-
eral not be C^. Moreover, they will not even have a continuous tangent plane.
The rigidity of the C^ condition can be a serious obstacle in the design of surfaces
that consist of a network of Bezier patches (or of piecewise polynomial patches
in other representations).

16.1 Smoothness and Subdivision 287
Figure 16.2 C^ continuous Bezier patches: two C^ bicubic patches.
We already saw how to use blossoms to subdidivide Bezier patches using
(14.15).
Here we treat an important special case more geometrically. Suppose
the domain rectangle of a Bezier patch is subdivided into two subrectangles by
a straight line u = u. That line maps to an isoparametric curve on the patch,
which is thus subdivided into two subpatches. We wish to find the control nets
for each patch. These two patches, being part of one global surface, meet with C"
continuity. Therefore, all their rows of control points must be control polygons
of C" piecewise ^th degree curves. Those curves are related to each other by the
univariate subdivision process from Section 5.4.
We now have the following subdivision algorithm: interpret all rows of the
control net as control polygons of Bezier curves. Subdivide each of these curves
2itu = u. The resulting control points form the two desired control nets. For an
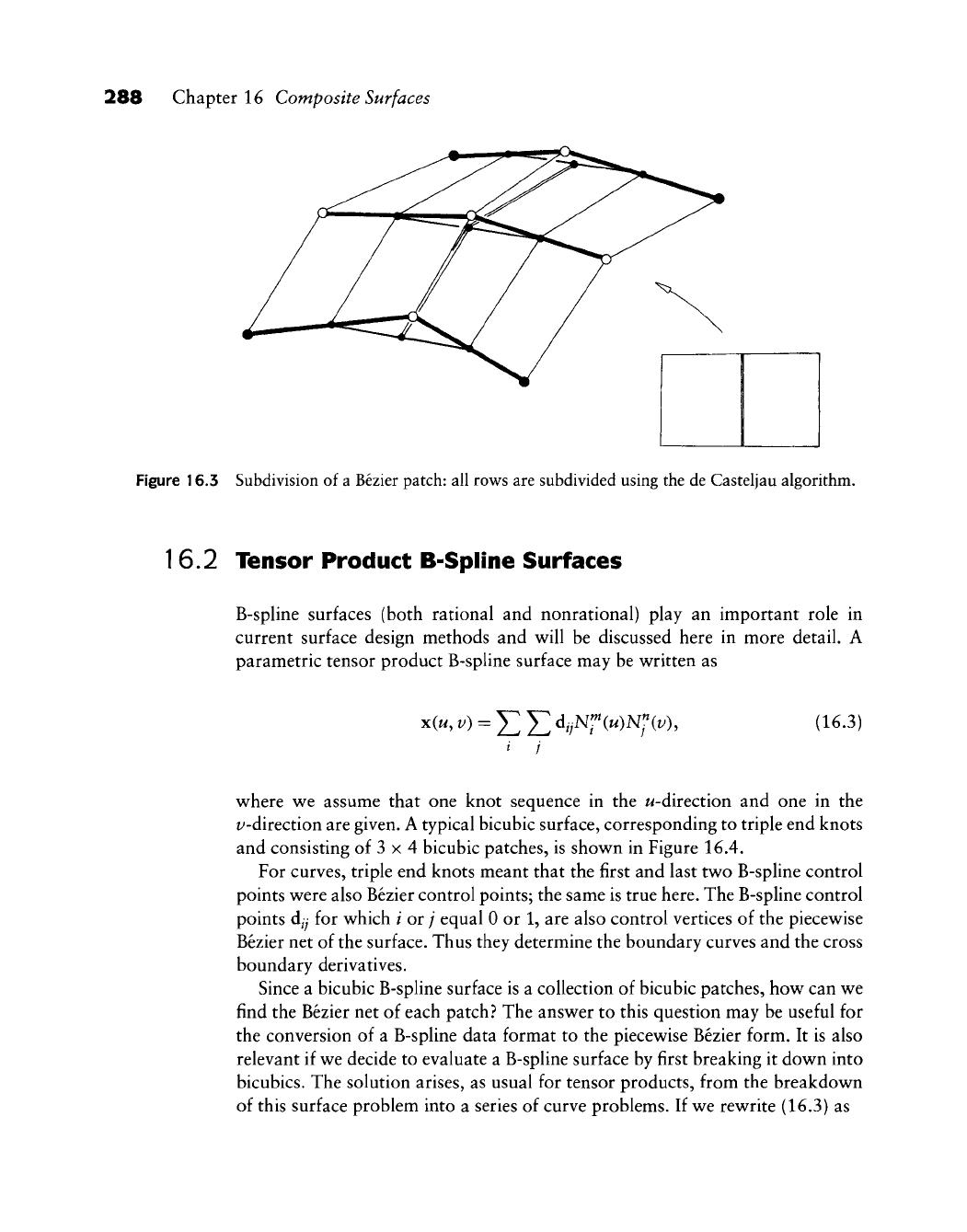
example, see Figure 16.3.
Subdivision along an isoparametric line v = v\s treated analogously. If we want
to subdivide a patch into four subpatches that are generated by two isoparametric
lines u = u and
i^
=
z),
we apply the subdivision procedure twice. It does not matter
in which direction we subdivide first.
288 Chapter 16 Composite Surfaces
Figure 16.3 Subdivision of a Bezier patch: all rows are subdivided using the de Casteljau algorithm.
1
6.2 Tensor Product B-Spline Surfaces
B-spline surfaces (both rational and nonrational) play an important role in
current surface design methods and will be discussed here in more detail. A
parametric tensor product B-spline surface may be written as
x(i«,
v)
= Y,Y. di,Nf (M)N«(i;),
(16.3)
where we assume that one knot sequence in the w-direction and one in the
^/'direction are given. A typical bicubic surface, corresponding to triple end knots
and consisting of 3 x 4 bicubic patches, is shown in Figure 16.4.
For curves, triple end knots meant that the first and last two B-spline control
points were also Bezier control points; the same is true here. The B-spline control
points dij for which / or / equal 0 or 1, are also control vertices of the piecewise
Bezier net of the surface. Thus they determine the boundary curves and the cross
boundary derivatives.
Since a bicubic B-spline surface is a collection of bicubic patches, how can we
find the Bezier net of each patch? The answer to this question may be useful for
the conversion of a B-spline data format to the piecewise Bezier form. It is also
relevant if we decide to evaluate a B-spline surface by first breaking it down into
bicubics. The solution arises, as usual for tensor products, from the breakdown
of this surface problem into a series of curve problems. If we rewrite (16.3) as

16.2 Tensor Product B-Spline Surfaces 289
Figure 16.4 Bicubic B-spline surfaces: a surface consisting of 3 x 3 patches together with its control
net.
x(u,v) =
Y,NT(^^
EW(")
we see that for each i the sum in square brackets describes a B-spHne curve in
the variable u. We may convert it to Bezier form by using the univariate methods
described in Chapter 8. This corresponds to interpreting the B-spline control
net rov^ by rov^ as univariate B-spline polygons and then converting them to
piecev^ise Bezier form. The Bezier points thus obtained may be interpreted—
column by column—as B-spline polygons, v^hich we may again transform to
Bezier form one by one. This final family of Bezier polygons constitutes the
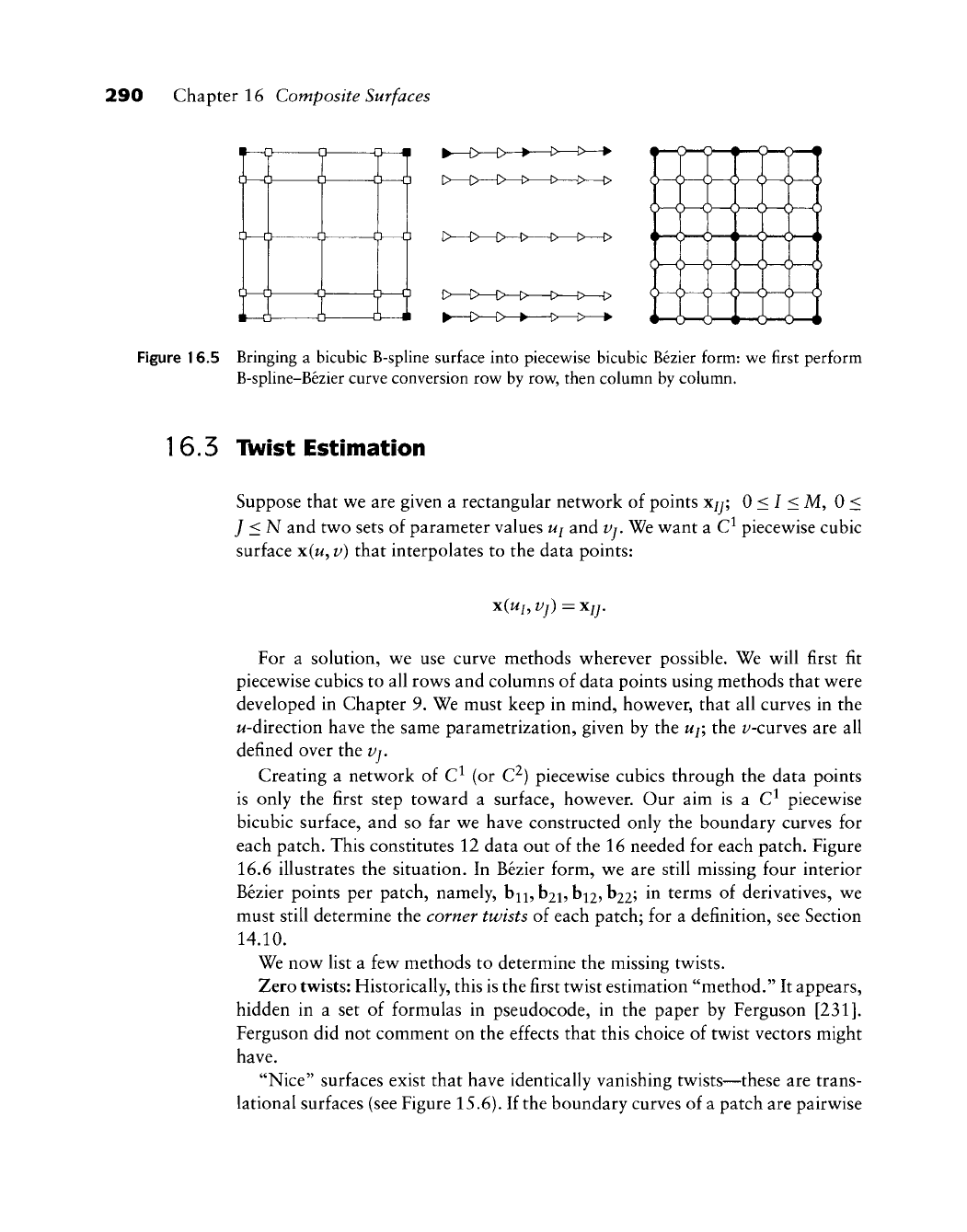
piecewise Bezier net of the surface, as illustrated in Figure 16.5.
Needless to say, we could have started the B-spline-Bezier conversion process
column by column. From the Bezier form, we may now transform to any other
piecewise polynomial forms, such as the piecewise monomial or the piecewise
Hermite form.
B-spline curves may be open or closed; the same is true for surfaces. Yet B-
spline surfaces may be closed in two different ways: we may form surfaces with
the connectivity of a cylinder or with that of a torus. No tensor product surface,
however, can have the connectivity of a "double torus" or more complicated
surfaces. In fact, even a surface with the topology of a sphere is not representable
as a tensor product surface, at least not as one without degeneracies.
290 Chapter 16 Composite Surfaces
0—g
n—rt
0 0—0
Figure 16.5 Bringing a bicubic B-spline surface into piecewise bicubic Bezier form: we first perform
B-spline-Bezier curve conversion row by row, then column by column.
1
6.5 IWist Estimation
Suppose that we are given a rectangular network of points x/y; 0 < I < M, 0 <
J <N and two sets of parameter values uj and Vj, We want a C^ piecewise cubic
surface x(w, v) that interpolates to the data points:
x(Ui, Vj) = Xjj.
For a solution, we use curve methods wherever possible. We will first fit
piecewise cubics to all rows and columns of data points using methods that were
developed in Chapter 9. We must keep in mind, however, that all curves in the
^/-direction have the same parametrization, given by the
Uj;
the i/-curves are all
defined over the Vj.
Creating a network of C^ (or C^) piecewise cubics through the data points
is only the first step toward a surface, however. Our aim is a C^ piecewise
bicubic surface, and so far we have constructed only the boundary curves for
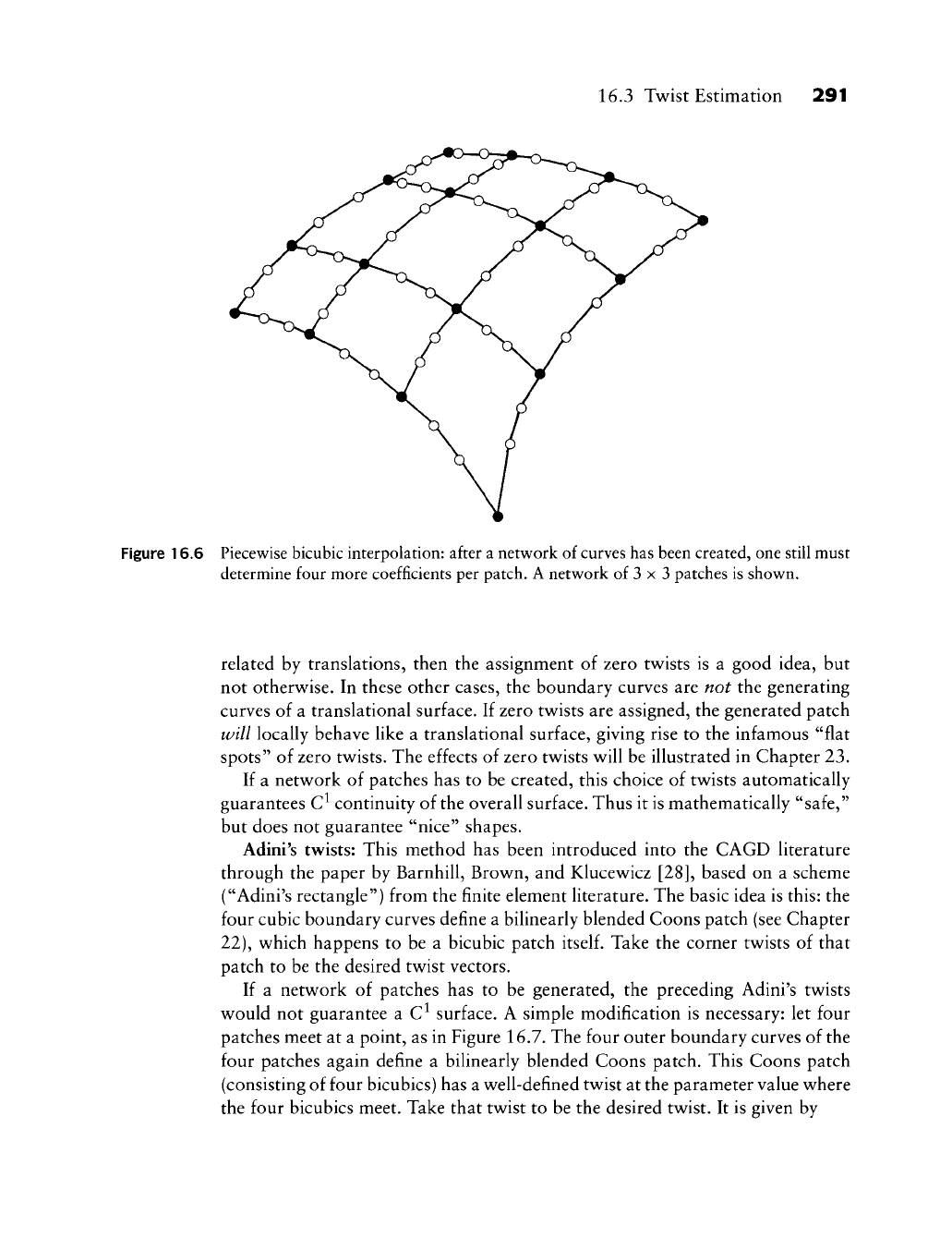
each patch. This constitutes 12 data out of the 16 needed for each patch. Figure
16.6 illustrates the situation. In Bezier form, we are still missing four interior
Bezier points per patch, namely, b^, b2i, bi25b22; in terms of derivatives, we
must still determine the corner twists of each patch; for a definition, see Section
14.10.
We now list a few methods to determine the missing twists.
Zero twists: Historically, this is the first twist estimation "method." It appears,
hidden in a set of formulas in pseudocode, in the paper by Ferguson
[231].
Ferguson did not comment on the effects that this choice of twist vectors might
have.
"Nice"
surfaces exist that have identically vanishing twists—these are trans-
lational surfaces (see Figure 15.6). If the boundary curves of a patch are pairwise
16.3 Twist Estimation 291
Figure 16.6 Piecewise bicubic interpolation: after a network of curves has been created, one still must
determine four more coefficients per patch. A network of 3 x 3 patches is shown.
related by translations, then the assignment of zero twists is a good idea, but
not otherwise. In these other cases, the boundary curves are not the generating
curves of a translational surface. If zero twists are assigned, the generated patch
will locally behave like a translational surface, giving rise to the infamous "flat
spots"
of zero twists. The effects of zero twists will be illustrated in Chapter 23.
If a network of patches has to be created, this choice of twists automatically
guarantees C^ continuity of the overall surface. Thus it is mathematically "safe,"
but does not guarantee "nice" shapes.
Adini's twists: This method has been introduced into the CAGD literature
through the paper by Barnhill, Brown, and Klucewicz [28], based on a scheme
("Adini's rectangle") from the finite element literature. The basic idea is this: the
four cubic boundary curves define a bilinearly blended Coons patch (see Chapter
22),
which happens to be a bicubic patch
itself.
Take the corner twists of that
patch to be the desired twist vectors.
If a network of patches has to be generated, the preceding Adini's twists
would not guarantee a C^ surface. A simple modification is necessary: let four
patches meet at a point, as in Figure 16.7. The four outer boundary curves of the
four patches again define a bilinearly blended Coons patch. This Coons patch
(consisting of four bicubics) has a well-defined twist at the parameter value where
the four bicubics meet. Take that twist to be the desired twist. It is given by
