Farin G. Curves and Surfaces for CAGD. A Practical Guide

Подождите немного. Документ загружается.

312 Chapter 17 Bezier Triangles

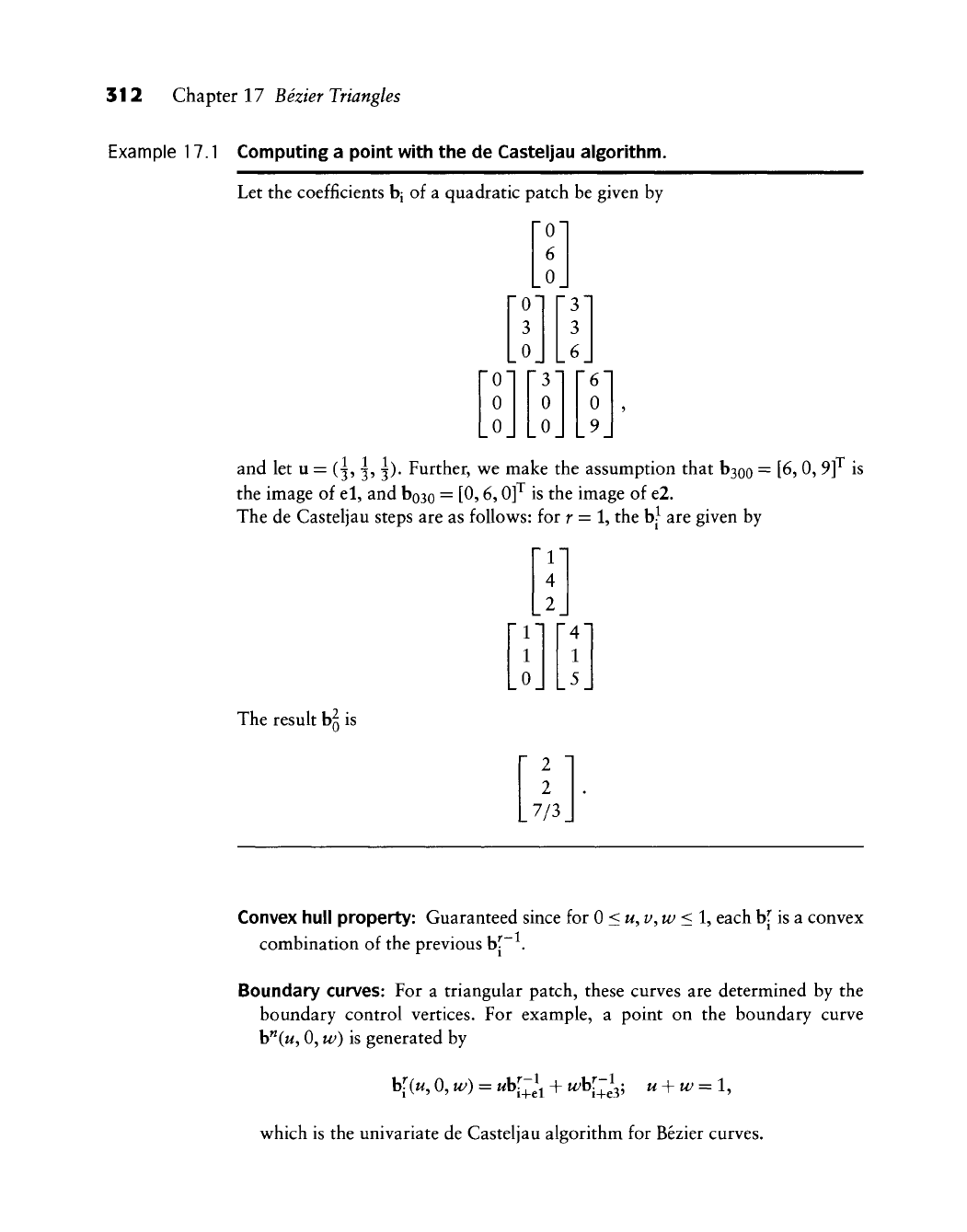
Example 17.1 Computing a point with the de Casteljau algorithm.

Let the coefficients bj of a quadratic patch be given by

and let u = (^, ^, ^). Further, we make the assumption that b3oo = [6, 0, 9]^ is

the image of el, and boao = [0, 6,0]^ is the image of e2.

The de Casteljau steps are as follows: for r = 1, the

b^^

are given by

The result bg is

7/3

Convex hull property: Guaranteed since for 0 <u^v,w <l, each b[ is a convex

combination of the previous b[~ .

Boundary curves: For a triangular patch, these curves are determined by the

boundary control vertices. For example, a point on the boundary curve

b"(w, 0, w) is generated by

b[(w, 0, w) = uhl~l^ +

^K+e3'

u + w=l,

which is the univariate de Casteljau algorithm for Bezier curves.

17.2 Triangular Blossoms 313

17.2 Triangular Blossoms

The blossoming principle was introduced in Section 4.4 and also proves useful

here.

Our development follows a familiar flavor: we feed different arguments

into the de Casteljau algorithm. At level r of the algorithm, we will use u^ as its

argument, arriving finally at level n, with the blossom value b[ui,...,

u„].

Note

that all arguments are triples of numbers, because they represent points in the

domain plane. The multivariate polynomial b[ui,..., u„] is called the blossom of

the triangular patch b(u). This blossom has all the properties that we encountered

earlier: it agrees with the patch if all arguments are equal: b(u) = b[u^"^] (recall

that u^^^ is short for w-fold repetition of u), it is multiaffine, and it is symmetric.

The last property is perhaps the least obvious one. We derived the symmetry

property of curve blossoms as a consequence of Menelaos' theorem; see Section

3.3.

A similar theorem holds when dealing with triangular blossoms: let bi; |i| =

n = 2 be an array of six control points, and let u and v be (the barycentric

coordinates of) two points. Then b[u, v] = b[v, uj.

This is seen by verifying that both expressions equal

boo2^3^3 + bo2o^2^2 +

^im^\^\

+ boi

1(^31^2

+ ^2^3)

+ bioi(Wil^3 +

Ui^Vi)

+ hxiQ{UiV2 + U2V{).

Let us consider a special case, namely, that of fixing one argument and letting

the remaining ones be equal, similar to the developments of polars in Section

5.6. So consider b[el,

u^"~^^].

We have to carry out one de Casteljau step with

respect to el, and then continue as in the standard algorithm. Since a step with

respect to el yields

biV)=b,+i,;^; |i|=^-l,

we end up with a triangular patch of degree n

— 1

whose vertices are the original

vertices with the exception of the bgy^—that row of control points is "peeled

off."

We may continue this experiment: if we next use e2, we peel off another layer

of coefficients, and so on. Let us use el / times, e2 / times, and e3 k times. We are

then left with a single control point:

bi = b[el<^'^, e2<^'^, e3<^^] |i| = n. (17.2)

So again the Bezier control points are obtainable as special blossom values!

We may also write the intermediate points of the de Casteljau algorithm as

special blossom values:

br(u) = b[u<^^, er^"^, e2<^'^,

e3<^^];

i^j + k^r = n, (17.3)

314 Chapter 17 Bezier Triangles

Figure 17.3 A curve on a surface: a line segment in the domain is mapped to a curve on a triangular

patch.

If we are interested in the control vertices Cj w^ith respect to a triangle with

vertices f

f2, f3, all we have to do is to evaluate the blossom:

q = b[fr^'^, f2<^'^,

£3^^^].

(17.4)

This relationship, without use of the blossoming principle, is discussed by Gold-

man [261] and by Boehm and Farin [81]. See also Seidel

[564].

The triangular analogue to the Leibniz formula (3.22) is as follows:

h[(at + Psr^'n = Yl ('')«')^""'b[r<^>,

s<"-^^].

(17.5)

i=o ^^^

There is an immediate practical ramification of this formula: suppose we are

given two points r and s in the domain. The straight line through them is mapped

to a curve of degree n on the triangular patch. This curve may be written as a

Bezier curve, and its Bezier points are given by

b[r^"^],

b[r^^~^^,

s],...,

b[s^"^].

See Figure 17.3.

If we use three points r, s, t in the domain, we obtain

b[(ar + ps + yt)<^>] = ^ ('''V^>y^b[r<^>,

s<^'>,

t<^>].

(17.6)

liM ^^^

Here, (^) is the generalized binomial coefficient and is defined as

iljlkl

and the summation Xliii=« i^ meant to sum over all triples (/,/, k) with /,/, ^ > 0

and

\i\

i~\-

j + k = n.

17.3 Bernstein Polynomials 315

17.5 Bernstein Polynomials

Univariate Bernstein polynomials are the terms of the binomial expansion of

[^ + (1

—

t)f. In the bivariate case, Bernstein polynomials B^ are defined by^

B'liu)

= r UV^^; |i| = n. (17.7)

We define B^{u) = 0 if /,/, ^ < 0 or /,/', k> n. This follows standard convention

for the trinomial coefficients (^). Some of the cubic Bernstein polynomials are

show^n in Figure 17.4.

As a further example, the quartic Bernstein polynomials may be arranged in

the following triangular scheme (corresponding to the control point arrangement

in the de Casteljau algorithm):

Gv^uP' lluv^w 6u^v^

4vw^ lluvw^ llu^vw 4u^v

w^ 4uw^ Gu^u?' 4u^w u^

Bernstein polynomials satisfy the following recursion:

B'liu) = uB\zl^{n) + vBlzl^{xx) +

wB^lzl^ixx)-,

|i| = n. (17.8)

This follows from their definition, as given in (17.7), and the use of the identity

Just as in the curve case, Bernstein polynomials may be used to define a Bezier

triangular patch:

b(u) - Y. MfCu). (17.9)

The proof is a straightforward application of (17.6) and the observation that

u = ut\ + vol +

wt?>.

2 Keep in mind that although

B^(u,

f, w) looks trivariate, it is not, since u-\-v-\-w = l.

316 Chapter 17 Bezier Triangles

Figure 17.4 Bernstein polynomials: the basis functions

^003'

^120 (^^P ^^^) ^^^ ^lll (hottom).

The intermediate points b[ in the de Casteljau algorithm may also be expressed

in terms of Bernstein polynomials:

br(u) = ^bi+jBr(u); \i\=n-r.

(17.10)

We can generalize (17.9) just as we could in the univariate case:

b«(u)= Y^ br(u)Bp''(u); 0<r<n, (17.11)

17.4 Derivatives

When we discussed derivatives for tensor product patches (Section 14.6), we

considered partials because they are easily computed for those surfaces. The

situation is different for triangular patches; the appropriate derivative here is the

directional derivative. Let u^ and

xxi

be two points in the domain. Their difference

d =

U2 —

Ui defines a vector.^ The directional derivative of a surface at x(u) with

respect to d is given by

Ddx(u) = lim — [x(u + d) -

x(u)].

d^o \a\

3 In barycentric coordinates, a point u is characterized hy u-\- v -\-w =

while a vector

d = (J,

f) is characterized hy d-\- e-\-f = 0.

17.4 Derivatives 517

Dax(u)

Figure 17.5 Directional derivatives: a straight line in the domain is mapped to a curve on the patch.

A geometric interpretation: in the domain, draw the straight line through u that

is parallel to d. This straight line will be mapped to a curve on the patch. Its

tangent vector at x(u) is the desired directional derivative; it is shown in Figure

17.5.

Using the proof technique from Section 5.3, we obtain

Ddb(u) = nh[d,

u^"-^^].

(17.12)

Equation (17.12) has two possible interpretations, just as in the curve case. We

may perform one step of the de Casteljau algorithm with respect to the direction

vector d, and n

—

1 more with respect to the position u:

DM^)

= n

J2 W(d)Br^(u). (17.13)

\i\=n-l

Alternatively, we may first carry out «

—

1 de Casteljau steps and then follow up

with one step with respect to d:

Ddb(u) = n(db"^-^ +

eh"^-^

/1>^3-l).

(17.14)

We may continue taking derivatives, arriving at:

D^jb(u) = -^h[d<^>,

„<"—].

(17.15)

—

r):

The rth directional derivative at b(u) is therefore found by performing r steps of

the de Casteljau algorithm with respect to d, and then by performing n

—

r more

steps with respect to u. Of course, it is irrelevant in which order we take these

steps (first noted in [188]).

In the same way, we may compute mixed directional derivatives: if dj and 62

art two vectors in the domain, then their mixed directional derivatives are

318 Chapter 17 Bezier Triangles

D'f. b(u) = b[d<^^,d<^>,u<"-^-^>]. (17.16)

This blossom resuh may also be expressed in terms of Bernstein polynomials.

Taking n

—

r steps of the de Casteljau algorithm with respect to u, and then r

more with respect to d gives

D^jb«(u) = -^ T h"-\u)BUd). (17.17)

—

r)l ,T-^ ^ ^

\]\=r

Or we might have taken r steps with respect to d first, and then n

—

r ones with

respect to u. This gives:

D'h"(u)^-^

T hUd)B"-''(u). (17.18)

\\=n-r

Let us now spend some time interpreting our results. First, we note that (17.17)

is the analogue of (5.21) in the univariate case. This sounds surprising at first,

since (17.17) does not contain differences. Recall, however, that some of the

components of d must be negative (since J + ^ +

= 0). Then the B|'(d) yield

positive and negative values. We may therefore view terms involving B-'(d) as

generalized differences. Similarly, (17.18) may be viewed as a generalization of

the univariate (5.24).

For r = 1, the terms b^d) in (17.18) have a simple geometric interpretation:

since bKd) = ^bj_^ei + ^\-\-^i + /bj+e3 ^^d

|j|

w —

1, they denote the affine map

of the vector d e E^ to the triangle formed by bj_^ei, bj+e2?

bj+e3-

The directional

derivative of b" is thus a triangular patch whose coefficients are the images of

d on each subtriangle in the control net (see Figure 17.6). For computational

purposes, we would compute the net of the wb^d) and use them as the input for

a de Casteljau algorithm of an (n

—

1)^^ degree Bezier patch.

Similarly, let us set r = 1 in (17.17). Then,

Ddb"(u) = «^bj'-i(u)B;(d)

1)1=1

= «(Jb«,-i + eb^2"' + ^b«3-i).

Since this is true for all directions d

E^, it follows that b^^\ ^^a^^

^^3"^

define

the tangent plane at b'^(u). This is the direct generalization of the corresponding

univariate result. In particular, the three vertices bo^„^o?bo,w-i,i?bi^^_i

span the

tangent plane at bo^^^o with analogous results for the remaining two corners.

Again, we see that the de Casteljau algorithm produces derivative information

17.4 Derivatives 319

Figure 17.6 Directional derivatives: a vector d in the domain (bottom right) is mapped to the control

net subtriangles to form the vectors bj^(d).

Example 17.2 Computing a directional derivative.

Let the coefficients bj of a quadratic patch be those from Example 18.1. Let us

pick the direction d =

(1,

—

1).

We can then compute the bj^(d):

[3'

'3'

•31

If we now evaluate at u = ( 3, 3, ^ 1, we obtain the vector

which must still be multiplied by a factor oin

—

l = 2to obtain the directional

derivative D(i^o,-i)b^ (i h l)'

Alternatively, we might have taken the hj from Example 17.1 and evaluated them

at d. The result is the same!

as a by-product of the evaluation process; see Example 17.2 for a numerical

example.

We next discuss cross boundary derivatives of Bezier triangles. Consider the

edge

= 0 and a direction d not parallel to it. The directional derivative with

320 Chapter 17 Bezier Triangles

Figure 17.7 Cross boundary derivatives: any first-order cross boundary directional derivative of a

quartic, evaluated along the indicated edge, depends only on the two indicated rows of

Bezier points.

respect to d, evaluated along

= 0, is the desired cross boundary derivative. It

is given by

D',h\u)

u=o

{n-r)\

(u)

\\Q\=n-r

M=0

(17.19)

where

= (0,/, k). Since u = (0, v, w) = (0, v,l

—

v), this is a univariate expres-

sion, that is, a Bezier curve in terms of barycentric coordinates. Note that it

depends only on the r + 1 rows of Bezier points closest to the boundary under

consideration. Analogous results hold for the other two boundaries; see Figure

17.7.

This result is the straightforward generalization of the corresponding uni-

variate result. We will use it for the construction of composite surfaces, just as

we did for curves.

17.5 Subdivision

We will later study surfaces that consist of several triangular patches forming

a composite C surface. Now, we start with a surface consisting of just two

triangular patches. Let their domain triangles be defined by points a, b, c, d, as

shown in Figure 17.8. If the common boundary is through b and c, then the

(domain!) point d can be expressed in terms of barycentric coordinates of a, b, c:

d = v^a + Vih + f

3C.

17.5 Subdivision 321

Figure 17.8 Subdivision: the domain geometry.

Suppose now that a Bezier triangle b" is given that has the triangle a, b, c as

its domain, such that we have barycentric coordinates a = el, b = e2, c = e3. Of

course, the patch is defined over the whole domain plane, in particular over the

triangle d, c, b. What are the Bezier points Cj of b" if we consider only the part

of it that is defined over d, c, b?

The answer was already given with (17.4):

q = b[d<^^,

e2<^=^,

e3^^^];

i + j + k = n. (17.20)

So all we have to do is compute the point b(d) using the de Casteljau algorithm,

and the intermediate points are the desired patch control vertices!

Some of the Cj deserve special attention: the common boundary of the two

patches is characterized hyu = 0. The Bezier points of the corresponding bound-

ary curve must be same for both patches; we have

Cj„ = b[e2<'>,e3<*>] = bj,; i + k = n, (17.21)

where Jo = (0,/, k). We also have

c„oo =

b[d<">],

thus asserting, as expected, that we find c„oo ^s a point on the surface, evaluated

at d. A numerical example is given in Example 17.3.

We thus have an algorithm that allows us to construct the Bezier points of the

"extension" of

to an adjacent patch. It should be noted that this algorithm does

not use convex combinations (when d is outside a, b, c). It performs piecewise

linear extrapolation, and should therefore not be expected to be numerically very

stable.

If d is inside a, b, c, then we do use convex combinations only, and (17.20)

provides a subdivision algorithm. Just as d subdivides the triangle a, b, c into

three subtriangles, the point b"(d) subdivides the triangular patch into three