Farin G. Curves and Surfaces for CAGD. A Practical Guide
Подождите немного. Документ загружается.


342 Chapter 18 Practical Aspects of Bezier Triangles
• O •
• • • •
Figure 18.4 The nine-parameter interpolant: nine of its ten Bezier ordinates are directly determined
from the given data.
location aon in the x,
}/-plane
is given by
2 1
^012 =
:TX003
+
:;Xo305
v^here XQOS and X030 are given data sites (relabeled here for convenience). The
given tangent plane at
XQOS
is of the form z{x^ y) =
Z003
+ ^^003 +
!V^003?
where
Zoo3,
^003? "^003 ^^^ given position, x- and y-partials. Then wt simply have to
evaluate that plane at a and we have fcoi2-
boi2 = z(a).
The remaining Bezier ordinates are found in the same
w^ay.
Note that this process
is simply univariate cubic Hermite curve interpolation as outlined in Section 7,51
The tenth coefficient, bm/is not determined by the data. It is independent of
the prescribed data and can be assigned any arbitrary value. A reasonable choice
is to select ^i 11 such that quadratic precision of the interpolant is maintained,
that is, if the nine prescribed data w^ere read off from a quadratic, then the
interpolant would reproduce this quadratic. If a quadratic is degree elevated to
cubic, the coefficient bm may be expressed as
1
^1,1,1
==
7(^2,0,1 + ^1,0,2 + ^2,1 + Vl,2 + ^2,1,0 + ^1,2,0)
-^(Ko,0 + V3,0 + Vo,3)- (18.4)
Thus choosing biii according to (18.4) ensures quadratic precision of the
interpolant. P. Alfeld"^ has pointed out that other choices of b^ii also ensure
4 Private communication, 1985.

18.5 The Clough-Tocher Interpolant 343
• • •
• O o •
• • o • «
• •••••
Figure 18.5 Quintic C^ interpolants: the solid points are derived from the C^ data at the vertices; the
open ones have to be chosen in order to ensure C^ continuity across patch boundaries.
quadratic precision; it is an open question if any of these choices can be sensibly
labeled "best."
In a situation where data are prescribed at several triangles in a triangulation,
the preceding interpolant has a serious drawback: it requires C^ data, but the
produced overall surface is only C^. You are invited to construct an example!
If we insist on C^ continuity, we could raise the degree from three to five.
We then have to prescribe position, two first and three second derivatives at
the vertices of each triangle. This fixes 18 of the quintic's 21 coefficients. The
remaining three are used to ensure C^ continuity between neighboring patches,
in the same way as described later for the Clough-Tocher interpolant. This
method for C^ interpolation is described in detail in [29]; see Figure 18.5 for
an illustration. Again, we have the drawback that second-order information has
to be supplied, yet only first-order smoothness is obtained.
18.5 The Clough-Tocher Interpolant
This interpolant is conceptually the simplest of all so-called split-triangle inter-
polants^ and it has been known in the finite element literature for some time; see
Strang and Fix
[582].
It is characterized by the "simplest" symmetric split of a
triangle: each vertex is joined to the triangle's centroid; thus a macro-triangle^ is
split into three mini-triangles. Any other interior point other than the centroid
would do; the centroid is chosen for symmetry reasons.
5 The given triangles in a triangulation are referred to as macro-triangles in order to
differentiate between them and the triangles resulting from the splitting process, the mini-
triangles.

344 Chapter 18 Practical Aspects ofBezier Triangles
The first-order data that this interpolant requires are position and gradient
value at the vertices of the macro-triangle plus some cross-boundary derivative
at the midpoint of each edge. The prescribed cross-boundary derivative could
be in any direction not parallel to its edge; but since adjacent macro-triangles
should share the same data along the common edge, it is most natural to choose
the direction perpendicular to that edge. We then speak of a cross-boundary
normal derivative.
In summary, we have 12 data per macro-triangle. It is easily seen that inter-
polation to this data produces a globally C^ surface if cubic polynomials are
employed over each mini-triangle.
We shall nov^ turn to the description of the actual interpolant; w^e refer to
Figure 18.6. The Bezier ordinates of the three boundary curves (marked by full
circles) are found exactly as for the nine-parameter interpolant. The next "layer"
of ordinates, marked by full circles and diamonds, is determined if v^e enforce
interpolation to the cross-boundary derivatives: the cross-boundary derivative,
evaluated along an edge, is a univariate quadratic polynomial. It can be v^ritten
as a univariate Bezier polynomial with three coefficients according to (17.19).
The first and last of the three coefficients is determined by the gradients at the
vertices, the center one as well by the cross-boundary derivative at the midpoints
of that edge.
We are still left with the task of specifying the ordinates marked by open cirlces
in Figure 18.6. Since the interpolant must be C^ over each macro-triangle, those
ordinates must satisfy the C^ conditions. Thus each of the three outer ordinates
of the four ones under consideration must be the average of the adjacent three
ordinates that have already been determined. Finally, the center ordinate must
be the average of the three just found.
In many applications, we will not be given the required cross-boundary deriva-
tives at the edge midpoints. The most obvious method to estimate this derivative
Figure 18.6 The Clough-Tocher interpolant: each macro-triangle is split into three mini-triangles.
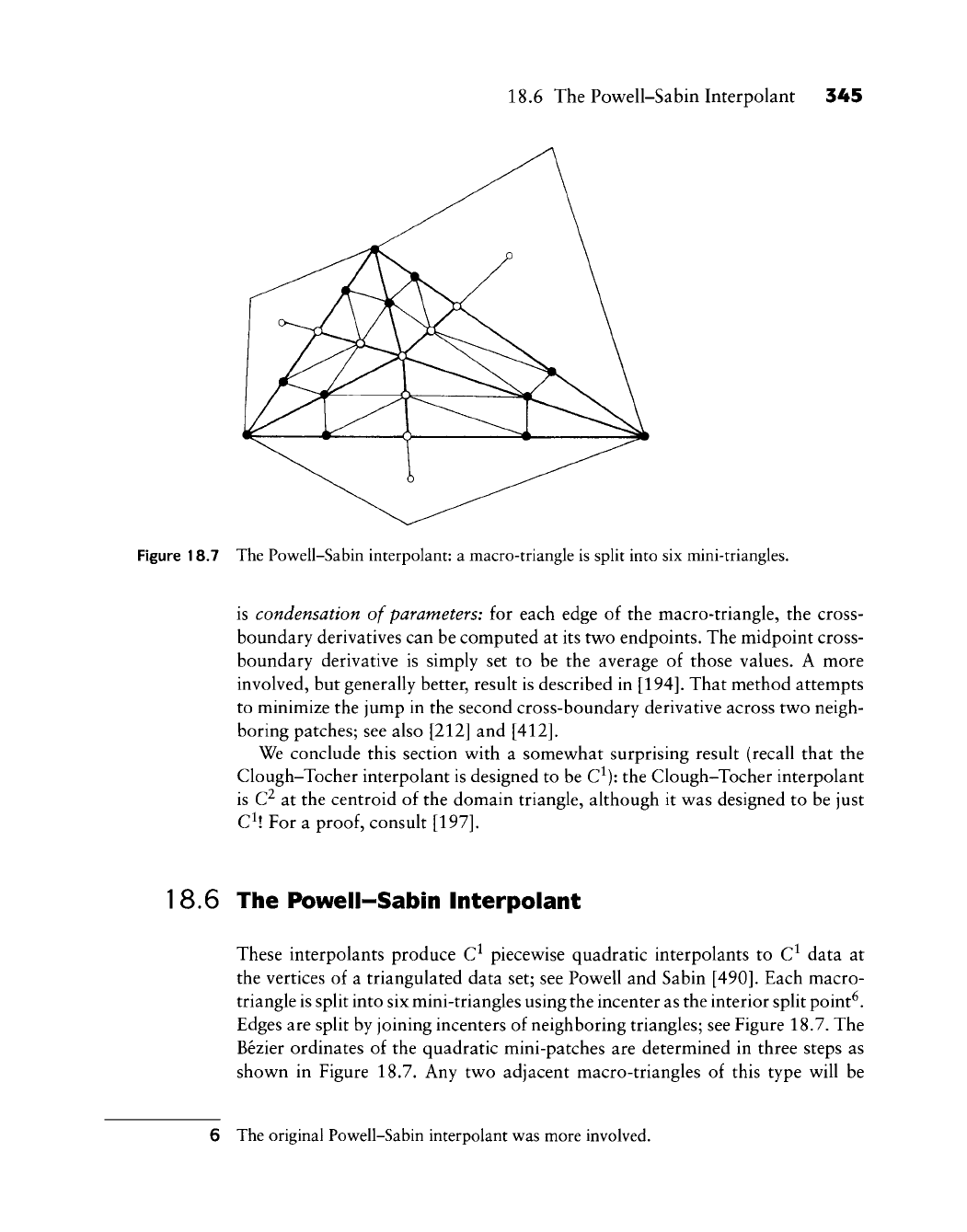
18.6 The Powell-Sabin Interpolant 345
Figure 18.7 The Powell-Sabin interpolant: a macro-triangle is split into six mini-triangles.
is condensation of parameters: for each edge of the macro-triangle, the cross-
boundary derivatives can be computed at its two endpoints. The midpoint cross-
boundary derivative is simply set to be the average of those values. A more
involved, but generally better, result is described in
[194].
That method attempts
to minimize the jump in the second cross-boundary derivative across tv^o neigh-
boring patches; see also [212] and
[412].
We conclude this section w^ith a somewhat surprising result (recall that the
Clough-Tocher interpolant is designed to be C^): the Clough-Tocher interpolant
is C^ at the centroid of the domain triangle, although it was designed to be just
C^! For a
proof,
consult
[197].
18.6 The Powell-Sabin Interpolant
These interpolants produce C^ piecewise quadratic interpolants to C^ data at
the vertices of a triangulated data set; see Powell and Sabin
[490].
Each macro-
triangle is split into six mini-triangles using the incenter as the interior split point^.
Edges are split by joining incenters of neighboring triangles; see Figure 18.7. The
Bezier ordinates of the quadratic mini-patches are determined in three steps as
shown in Figure 18.7. Any two adjacent macro-triangles of this type will be
6 The original Powell-Sabin interpolant was more involved.

346 Chapter
18
Practical Aspects ofBezier Triangles
differentiable across their common edge:
by
construction, each cross-boundary
derivative
is
just
one
hnear function instead
of
being piecev^ise hnear.
The Pov^ell-Sabin interpolant uses more triangles than does
the
Clough-
Tocher method—but
it is
easier
to
contour. Each Pow^ell-Sabin patch
is a
qua-
dratic
of the
form
z = f(x, y), and a
contour
is of the
form
c =
/"(x, y), that
is, a
conic. This conic
may be
v^ritten
as a
rational quadratic Bezier curve according
to Chapter
12. Its
Bezier points
and
w^eights
may be
determined
by
solving
a
number
of
quadratic equations;
see
[619].
18.7 Least Squares
Although
w^e
covered interpolation methods
so far,
approximation is
a
possibility
as v^ell.
In
that context,
we
v^ould
be
given
a
triangle
in
the
x,
3;-plane
and a set of
points ui,...,
Up
in the x,
y-plane, expressed
in
terms
of
barycentric coordinates
of the given triangle. Each
of
these points
has a
function value
Zj
associated v^ith
it.
We now^
seek
a
triangular functional Bezier patch
of a
given degree
n
that
approximates
the
given data:
^fe^EMfCu*). (18.5)
\i\=n
In order
to
tackle this problem,
wt
linearize this equation, similar
to
the approach
of Section 15.6. With
L =
{n-\-l)(n-\-2)
/2,
a
linearized version
of
(18.5) becomes
Zk^[B",,„(uk)
...
B«„oo("*)]
boOn
L
bnOO
(18.6)
There
are
several v^ays
to
construct
the
linearization;
a
simple
one
v^ould
be the
foUow^ing:
For
the
case
w
= 2, it
v^ould produce this ordering
of
indices:
(0,0,2),
(1,0,1), (2,0,0), (0,1,1), (1,1,0), (0,2,0).
Combining
all P
equations (18.6),
we
obtain
a
linear system

18.8 Problems 347
•^"oo«("i)
We abbreviate it as
B«oo("i)
^"„nn("L)J
Mb:
boOn
L b„QQ,
Zl
L^LJ
(18.7)
noting that M has many more rows than columns. The optimal solution to our
problem is obtained by solving the system of normal equations
M^Mb = M^z. (18.8)
It is also possible to formulate this type of least squares approximation for
the parametric case. Then, the function values
Zk
are replaced by data points p^
with associated parameter values u^.
18.8 Problems
1 Suppose that in Figure 18.1 we prescribed p instead of the three qj. We
could then find several sets of weights. Can that idea be generalized to
higher degrees?
2 Discuss how we could add shape equations to the least squares problem of
Section 18.7, in analogy to the approach taken in Section 15.6.
* 3 The Clough-Tocher interpolant turns out to be C^ at the centroid "for
free."
What can you say about the Powell-Sabin interpolant?
PI Non-split interpolants of degrees higher than three or five may be de-
fined for triangular patches. Experiment. Try to reproduce the Runge phe-
nomenon.
P2 Program up a triangulation algorithm for a 2D point set.
P3 Write a routine for constructing the Powell-Sabin interpolant over a 2D
triangulation.
This Page Intentionally Left Blank

W. Boehm
Differential
Geometry
II
19.1 Parametric Surfaces and Arc Element
A surface may be given by an implicit form f{x^ y^z) = 0 or, more useful for
CAGD, by its parametric form
X = X(W, V) —
x(u^ v)
y(u, v)
z(u, v)
"-[:]
G[a,b]c:
(19.1)
where the cartesian coordinates x, y, z of a surface point are differentiable func-
tions of the parameters u and v and [a, b] denotes a rectangle in the w, i^-plane;
see Figure 19.1 (sometimes other domains are used, for example, triangles). To
avoid potential problems w^ith undefined normal vectors, we will assume
x^
A
x^
7^
0 for u
G
[a,
b],
that is, that both families of isoparametric lines are regular (see Section 10.1) and
are nowhere tangent to each other. Such a parametrization is called regular}
Any change r = r(u) of the parameters will not change the shape of the surface;
the new parametrization is regular if det[r^,
r^,]
/ 0 for u
G
[a,
b],
that is, if one
can find the inverse u = u(r) of r.
A regular curve u = u(^) in the
w,
i/-plane defines a regular curve x[u(^)] on the
surface. One can easily compute the (squared) arc element (see Section 10.1) of
1 Examples of irregular parametrizations are shown in Figures
14.11,
14.12, and
14.13.
349
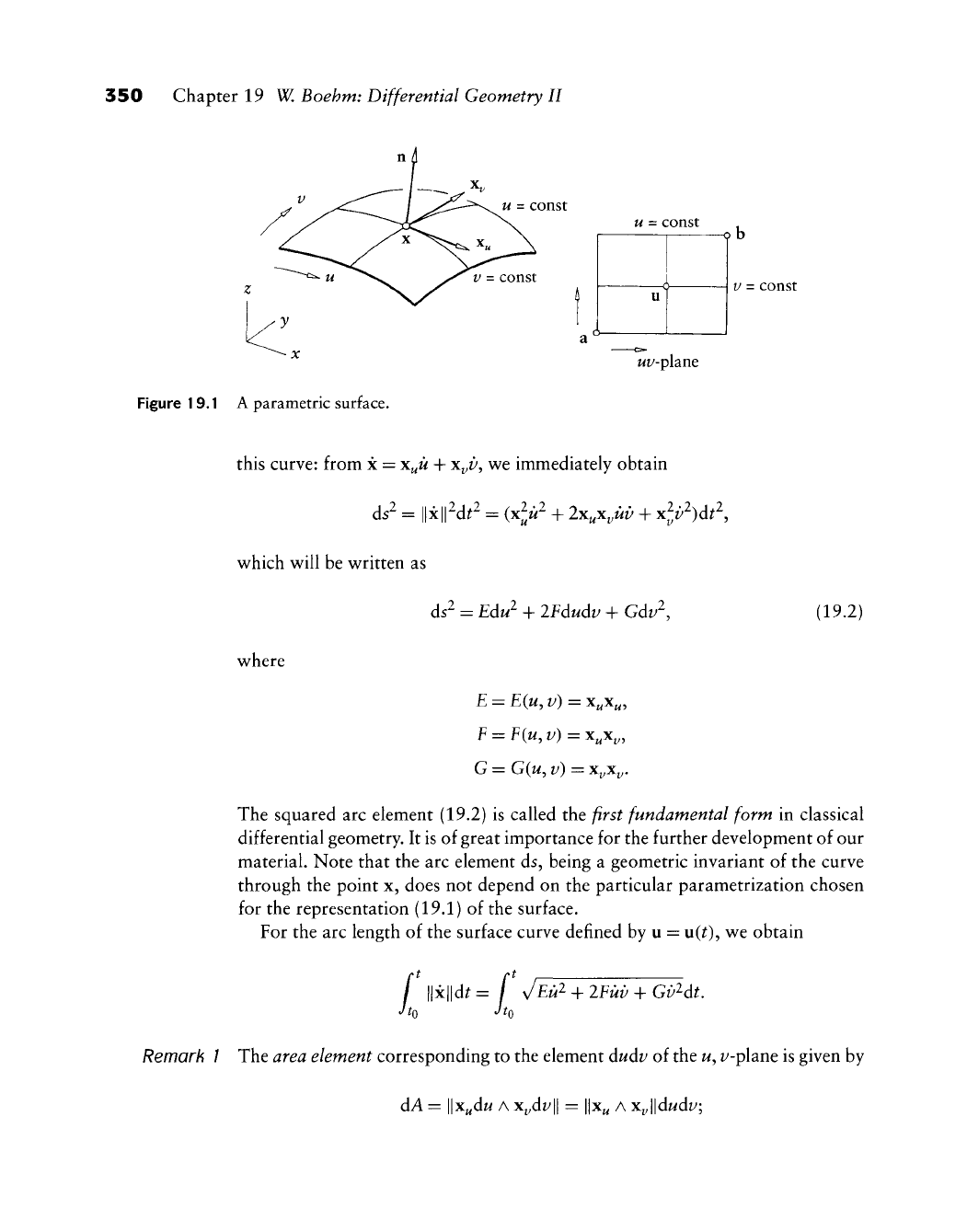
350 Chapter 19 W. Boehm: Differential Geometry II
u
=
const
V
=
const
Figure 19.1 A parametric surface.
u
=
const
0
uT
1
S
1
uv-plsine
V
=
const
this curve: from x = x^u + x^z), we immediately obtain
ds^
= ||x||^d^^ = (xlii^ + Ix^Xytiv + xlv^)dt^,
which will be written as
ds^
= Edu^ + IFdudv + Gdv^, (19.2)
where
E = E{u, v) = x^x^,
E = F(u, v) = x^Xy,
G = G(u, v) = x^x^.
The squared arc element (19.2) is called the first fundamental form in classical
differential geometry. It is of great importance for the further development of our
material. Note that the arc element ds, being a geometric invariant of the curve
through the point x, does not depend on the particular parametrization chosen
for the representation (19.1) of the surface.
For the arc length of the surface curve defined by u =
\x{t)^
we obtain
/
||x||d^=
f
JtQ Jto
^Eu^
+ lEuv + GiP^dt,
Remark / The area element corresponding to the element dudv of the
w,
i/-plane is given by
dA = llx^dw
A
x^dz/|| = ||x^
A
xjdudv;

19.1 Parametric Surfaces and Arc Element 351
u
m
du
Figure 19.2 Area element.
see Figure 19.2. From ||a
A
hf = aV - (ab)^, we obtain
D=||x„Ax,||=y£G-f2.
(19.3)
The quantity D is called the discriminant of (19.2). Thus the surface area A
corresponding to a region U of the
w,
i^-plane is given by
A
-IL^-
F^dudv.
Remark 2 If P = 0 at a point of the surface, the two isoparametric lines that meet there are
orthogonal to each other. Moreover, if f = 0 at every point of the surface, the
net of isoparametric lines is orthogonal everywhere.
Remark 5 Note that for any real^ du, dv, the first fundamental form ds^ is strictly positive.
However, if ds^ = 0, we have two imaginary directions. These are called isotropic
directions at x.
Remark 4 Let u^ = Vi\{ti) and
U2
= ^^liti) define two surface curves, intersecting at x. Both
curves are intersecting orthogonally if the polar form of x^, given by
X2X2 = EuiU2 + F{uiV2 + U2V\) -\- GviVi,
vanishes at x.
2 Note that the vector
[dw,
dv]
defines a direction at a point x.
