Farin G. Curves and Surfaces for CAGD. A Practical Guide
Подождите немного. Документ загружается.


352 Chapter 19 W, Boehm: Differential Geometry II
Figure 19.3 The local frame and the tangent plane.
1
9.2 The Local Frame
The partials x^ and x^ at a point x span the tangent plane to the surface at x. Let
y be any point on this plane. Then
det[y -
X,
x^, x^] = 0
is the implicit equation of the tangent plane. The parametric equation is
y(w, v) =x-\-
AuXj^
+ At/x^.
The normal x^
A
x^ of the tangent plane coincides with the normal to the surface
at X. The normalized normal
n=„''^'^''"„=7-KAxJ
llx^Ax^ll D
together with the unnormalized vectors x^, x^ form a local coordinate system,
a frame, at x (see Figure 19.3). This frame plays the same important role for
surfaces as does the Frenet frame (see Section 10.2) for curves. The normal is of
unit length and is perpendicular to x^ and Xj,, that is, n^ = 1 and nx^ =
nx^^
= 0.
In general, the local coordinate system with origin x and axes x^,
Xp
forms
only an affine system; it is also (unlike the Frenet frame) dependent on the
parametrization (19.1).
1
9.5 The Curvature of a Surface Curve
Let u(t) define a curve on the surface x(u). From curve theory we know that
its curvature
K
= ^ is defined by t^ = /cm; the prime denotes differentiation with

19.3 The Curvature of a Surface Curve 353
Figure 19.4 Osculating circle.
respect to the arc length of the curve. We will now reformulate this expression
in surface terms. Since t = x^ and u' = dw/ds, v' = dt'/ds, we have
t' = x'' = x^^iu'f + Ix^^u'v' + x^^iv'f + x^ + xy.
Let 0 be the angle between the main normal m of the curve and the surface normal
n at the point x under consideration, as illustrated in Figure 19.4. Then
t n = /cmn = K
COS
0.
Inserting t^ and keeping in mind that nx^ = nx^ = 0, we have
K
cos 0 =
nxj^j^{u')
+
2nXj^jjU^v^
+
nx^^{v^)'^.
(19.4)
Furthermore, nx^ = 0 implies n^^x^^ + nx^^ = 0, and so on. Thus, using the ab-
breviations
L = L(u, v) = -x^n^ = nx^^,
M = M(u,v) =-^(x^n^ + x^nJ = nx^^, (19.5)
N = N{u, v) = -XyXiy = nx^^,
Eq. (19.4) can be written as
K
cos 0 ds^ = Ldu^ + IMdudv + Ndv^, (19.6)
This expression is called the second fundamental form in classical differential
geometry. For any given direction du/dv in the
w,
^'-plane and any given angle 0,
the second fundamental form, together with the first fundamental form (19.2),

354 Chapter 19 W. Boehm: Differential Geometry II
allows us to compute the curvature /c of a surface curve having that tangent
direction.
Remark 5 Note that the arc length in the preceding development was only used in a
theoretical context; for applications, it does not have to be actually computed.
Remark 6 Note that
K
depends only on the tangent direction and the angle 0. It will change
its sign, however, if there is a change in the orientation of n.
19.4 Meusnier's Theorem
The right-hand side of (19.4) does not contain terms involving 0. For 0 = 0,
that is, cos 0 = 1, we have that m = n: the osculating plane of the curve is
perpendicular to the surface tangent plane at x. The curvature
KQ
of such a curve
is called the normal curvature of the surface at x in the direction of t (defined by
du/dv).
The normal curvature is given by
_
N
_ 1 _ ^^d fundamental form
Po 1st fundamental form
(19.7)
Now (19.6) takes the very short form
p =
Po
cos 0.
(19.8)
This simple formula has an interesting and important interpretation, known
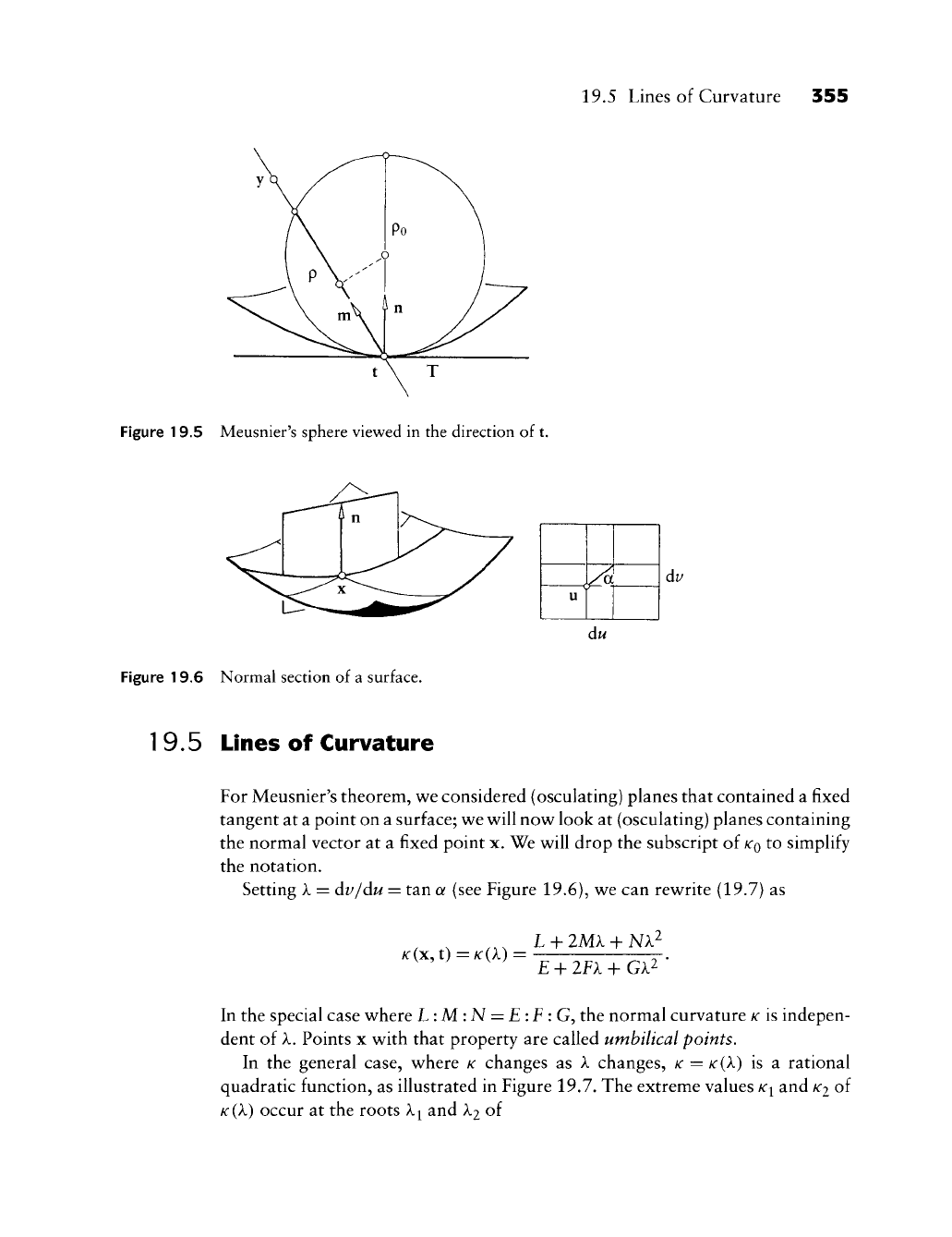
as Meusnier's theorem. It is illustrated in Figure 19.5: the osculating circles of
all surface curves through x having the same tangent t there form a sphere. This
sphere and the surface have a common tangent plane at x; the radius of the sphere
is Po-
As a consequence of Meusnier's theorem, it is sufficient to study curves at x
with m = n; moreover, these curves may be planar. Such curves, called normal
sections^ can be thought of as the intersection of the surface with a plane through
X and containing n, as illustrated in Figure 19.6.
Remark 7 If the direction of the normal is chosen as in Figure 19.5, we have 0 < p < po,
and p = 0 only if 0 = 7r/2, that is, if the osculating plane O coincides with the
tangent plane.
19.5 Lines of Curvature 355
Figure 19.5 Meusnier's sphere viewed in the direction of t.
u
A
dv
du
Figure 19.6 Normal section of a surface.
19.5 Lines of Curvature
For Meusnier's theorem, we considered (osculating) planes that contained a fixed
tangent at a point on a surface; we will now look at (osculating) planes containing
the normal vector at a fixed point x. We will drop the subscript of
KQ
to simplify
the notation.
Setting X = dv/du = tan a (see Figure 19.6), we can rewrite (19.7) as
In the special case where L:M:N = E:F :G^ the normal curvature
K
is indepen-
dent of
A.
Points x with that property are called umbilical points.
In the general case, where K changes as X changes, K =
K{X)
is a rational
quadratic function, as illustrated in Figure 19.7. The extreme values
/c^
and
KI
of
KQC)
occur at the roots Xi and
X2
of

356 Chapter 19 W, Boehm: Differential Geometry II
Figure 19.7 The function
K
=K(X).
ri2
det
-X 1
E F G
L M N
= 0.
(19.9)
It can be shown that
X^
and
X2
are always real. The extreme values
K^
and
K2
are
the roots of
det
KE
KF-
-L KF-M1_
M KG-N\~
(19.10)
The quantities X^ and X2 define directions in the u, i^-plane; the corresponding
directions in the tangent plane are called principal directions. The net of lines that
have these directions at all of their points is called the net of lines of curvature.
If necessary, it may be constructed by integrating (19.9).
Therefore, this net of lines of curvature can be used as a parametrization of
the surface; then (19.9) must be satisfied by dw = 0 and by Av = 0. This implies,
excluding umbilical points, that
F = 0 and M = 0.
The first equation, f = 0, states that lines of curvature are orthogonal to each
other; the second equation states that they are conjugate to each other as defined
in Section 19.9.
At an umbilical point, the principal directions are undefined; see also Re-
mark 9.
Remark 8 For a surface of revolution, the net of
lines
of curvature is defined by the meridians
and the parallels; an example is shown in Figure 19.8.

19.6 Gaussian and Mean Curvature 357
^ Parabolic
Hyperbolic
Figure 19.8 Lines of curvature on a torus. Also shown are the regions of eUiptic, parabolic, and
hyperbolic points.
19.6 Gaussian and Mean Curvature
The extreme values /c^ and
K2
oi
K
= /c(A) are called principal curvatures of the
surface at x. A comparison of (19.10) with /c^
—
(/c^ + K2)K +
KIKI
= 0 yields
LN-M^ ,._...
/Ci/C2= ^ 19.11
EG-F^
and
NE-2MP + LG
,.„..,
/C1+/C2 — . 19.12
The term K =
KIKI
is called Gaussian curvature^ whereas H =
^
(^l + ^l)
i^
called
mean curvature. Note that both
K\
and
/C2
change sign if the normal n is reversed,
but K is not affected by such a reversal.
If
K\
and
K2
are of the same sign, that is, if K > 0, the point x under considera-
tion is called elliptic. For example, all points of an ellipsoid are elliptic points. If
Ki and
/C2
have different signs, that is, K < 0, the point x under consideration is
called hyperbolic. For example, all points of a hyperboloid are hyperbolic points.
Finally, if either
/c^
= 0 or
A:2
= 0, iC vanishes, the point x under consideration is
called parabolic. For example, all points of a cylinder are parabolic points. In
the special case where both K and H vanish, one has a ^at point.
The Gaussian curvature K depends on the coefficients of the first and second
fundamental forms. It is a very important result, due to Gauss, that K can also be
expressed only in terms of £, F, and G and their derivatives. This is known as the
Theorema Egregium., which states that K depends only on the intrinsic geometry
of the surface. This means it does not change if the surface is deformed in a way
that does not change length measurement within it.

358 Chapter 19 W, Boehm: Differential Geometry II
Remark 9 All points of a sphere are umbilic. The Gaussian and mean curvatures of a sphere
are constant.
Remark W Any developable^ that is, a surface that can be deformed to planar shape without
changing length measurements in it, must have X = 0. Conversely, every surface
with K = 0 can be developed into a plane (if necessary, by applying cuts). See
also Section 19.10.
19.7 Euler's Theorem
The normal curvatures in different directions t at a point x are not independent
of each other. For simplicity, let the isoparametric curves of a surface be lines
of curvature; then we have P = M = 0 (see Section 19.5). As a consequence, we
have
L , N
/ci=-
and '<^2=-^^
and
K(X)
may be written as
^^^ L + NX^ E
K(X) = ^ ^ ., = Ki
+ ^21
Gk^
E + GX^ 'E + GX^ ^E + GA.2
(19.13)
The coefficients of
K-[
and KI have a nice geometric meaning: let ^ denote the
angle between x„ and the tangent vector x =
X„M
+ x^v of the curve under
consideration, as illustrated in Figure 19.9. We obtain
cos ^
—
xx„
VI
\n llxjl ^E
+
GX^
Line of curvature
Figure 19.9 Configuration for Euler's theorem.

and
sin vl/ = ^
19.8 Dupin's Indicatrix 359
^/GA.
llxll ||x,|| ^E + GA^'
where
A
= vju as before. Hence K(X) may be written as
K(X) = /ci cos^ ^ +
/C2
sin^ ^.
This important resuh was found by L. Euler.
19.8 Dupin's Indicatrix
Euler's theorem has the following geometric implication. If we introduce polar
coordinates r = ^p and ^ for a point y of the tangent plane at x by setting
y^
= ^
COS
^, ^2 = ^ sin ^, then setting ^\ = -^ and K2=
j--,
Euler's theorem
can be written
2 2
Pi Pi
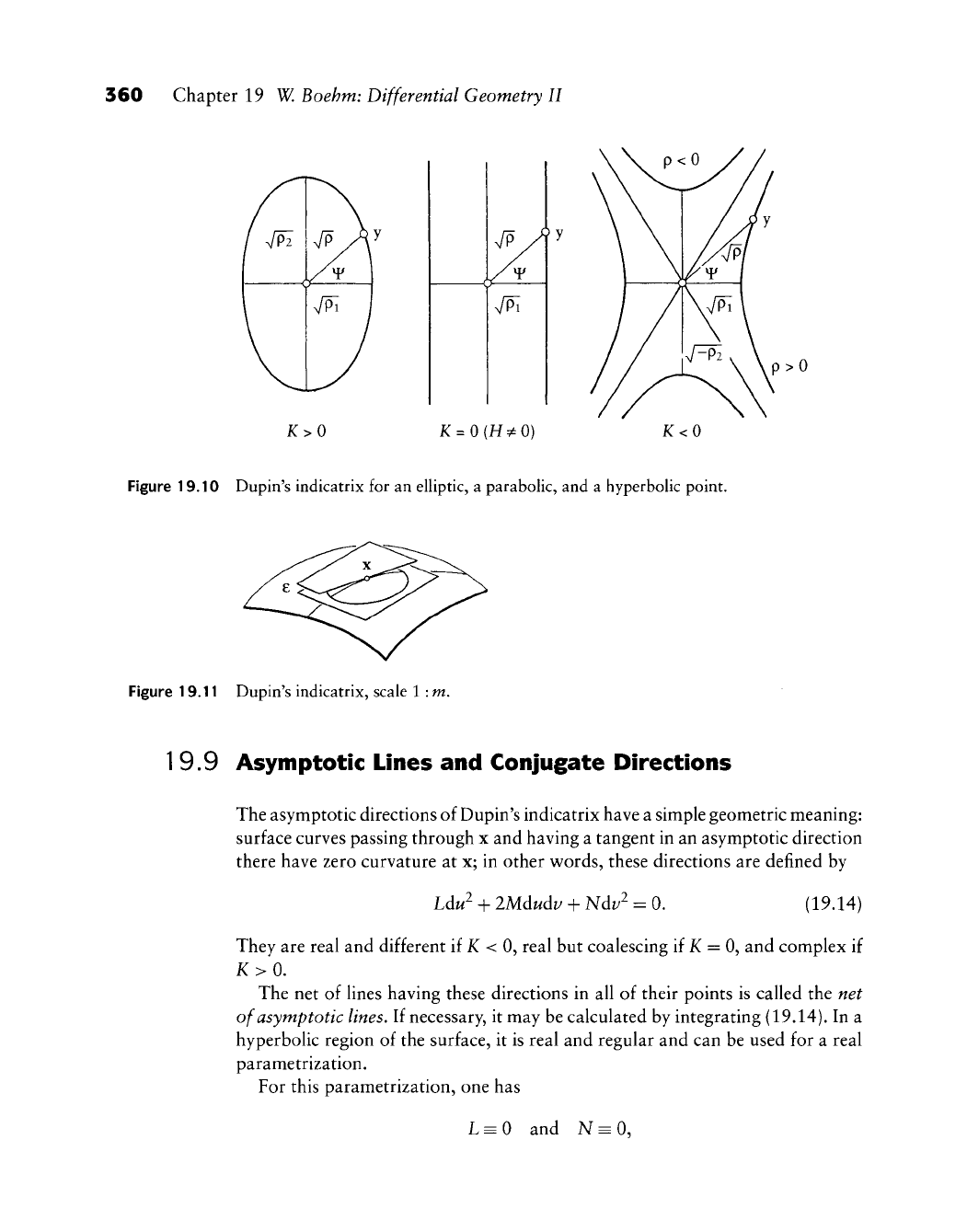
This is the equation of a conic section, the Dupin's indicatrix (see Figure 19.10).
Its points y in the direction given by ^ have distance ,y/p from x. Taking into
account that a reversal of the direction of n will effect a change in the sign of
p,
this
conic section is an ellipse if
i<C
> 0, a pair of hyperbolas if K < 0 (corresponding
to yp and ^—p), and a pair of parallel lines if X = 0 (but H ^ 0).
Dupin's indicatrix has a nice geometric interpretation: we may approximate
our surface at x by a paraboloid, that is, a Taylor expansion with terms up to
second order. Then Remark 7 of Chapter 10 leads to a very simple interpretation
of Dupin's indicatrix: the indicatrix, scaled down by a factor of 1
:
m, can be
viewed as the intersection of the surface with a plane parallel to the tangent
plane at x in the distance 6 = y^. This is illustrated in Figure
19.11.
Remark 11 This illustrates the appearance of a pair of hyperbolas in Figure 19.10; they
appear when intersecting the surface in distances 6 = ±y^. We can thus assign
a sign to the Dupin indicatrix, depending on its being "above" or "below" the
tangent plane.
360 Chapter 19 W. Boehm: Differential Geometry II
p>0
K>0
K
=
0(H^O)
K<0
Figure 19.10 Dupin's indicatrix for an elliptic, a parabolic, and a hyperbolic point.
Figure 19.11 Dupin's indicatrix, scale 1
:
m.
1
9.9 Asymptotic Lines and Conjugate Directions
The asymptotic directions of Dupin's indicatrix have a simple geometric meaning:
surface curves passing through x and having a tangent in an asymptotic direction
there have zero curvature at x; in other v^ords, these directions are defined by
Ldu^ + IMdudv + Ndv^ = 0. (19.14)
They are real and different if K < 0, real but coalescing if K = 0, and complex if
K>0.
The net of lines having these directions in all of their points is called the net
of asymptotic lines. If necessary, it may be calculated by integrating (19.14). In a
hyperbolic region of the surface, it is real and regular and can be used for a real
parametrization.
For this parametrization, one has
L = 0 and N = 0,

19.10 Ruled Surfaces and Developables 361
and vice versa.
As earlier, let y be a point on Dupin's indicatrix at a point x. Let y denote its
tangent direction at y. The direction y is called conjugate to the direction x from
X
to y. Consider two surface curves
\Xi{ti)
and 02(^2) ^hat have tangent directions
xi and
X2
at x. Some elementary calculations yield that x^ is conjugate to
X2
if
Liiiiii + M(^iz>2 + ^2^1) +
Nz>iZ>2
= 0.
Note that this expression is symmetric in u^,
U2.
By definition asymptotic direc-
tions are self-conjugate.
Remark 12 Isoparametric curves of a surface are conjugate if M = 0 and vice versa.
Remark 15 The principal directions, defined by (19.9), are orthogonal and conjugate; they
bisect the angles between the asymptotic directions; that is, they are the axis
directions of Dupin's indicatrix (see Figure 19.10).
Remark 14 The tangent planes of two "consecutive" points on a surface curve intersect in a
straight line s. Let the curve have direction t at a point x on the surface. Then s
and t are conjugate to each other. In particular, if t is an asymptotic direction, s
coincides with t. If t is one of the principal directions at x, then s is orthogonal to
t and vice versa. These properties characterize lines of curvature and asymptotic
lines and may be used to define them geometrically.
19.10 Ruled Surfaces and Developables
If a surface contains a family of straight lines, it is called a ruled surface. It is
convenient to use these straight lines as one family of isoparametric lines. Then
the ruled surface may be written
x = x(t,v)=p(t)-\-vq(t),
(19.15)
where p is a point and q is a vector, both depending on t. The isoparametric lines
t = const are called the generatrices of the surface; see Figure 19.12.
The partials of a ruled surface are given by
x^
= p + i^q and
x^^
= q. The normal
n at
X
is given by
n =
(p + t^q)
A
q
||(p + i/q)Aq||
A point y on the tangent plane at x satisfies
det[y - p, p, q] + zydet[y - p, q, q] = 0;
