Farin G. Curves and Surfaces for CAGD. A Practical Guide

Подождите немного. Документ загружается.

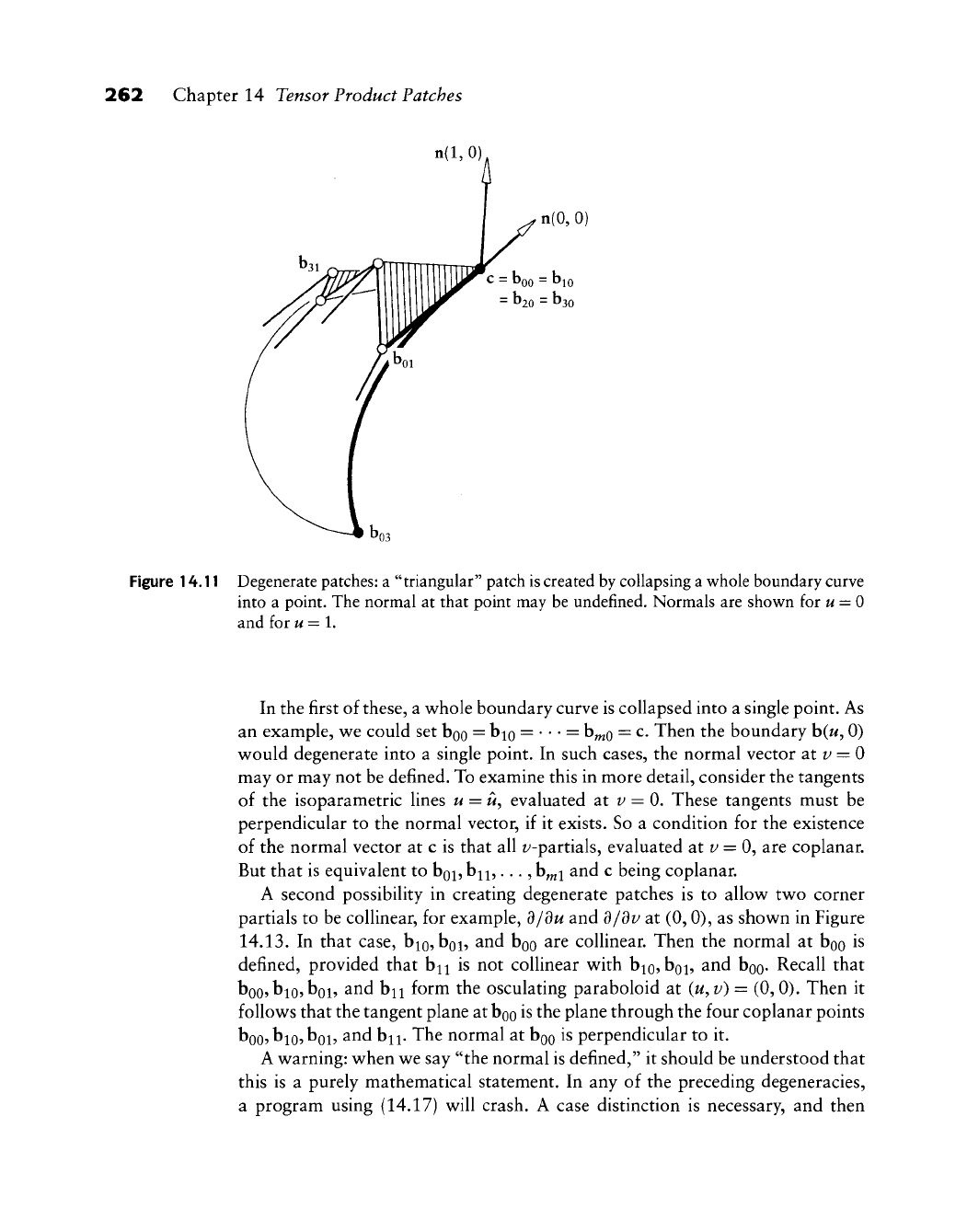
262 Chapter 14 Tensor Product Patches

n(l,0),

n(0,

c - boo - "10

= "20 = D30

Figure 14.11 Degenerate

patches:

a "triangular" patch is created by collapsing a whole boundary curve

into a point. The normal at that point may be undefined. Normals are shown for

= 0

and for u=l.

In the first of these, a whole boundary curve is collapsed into a single point. As

an example, we could set boo = b^o =

• • •

= b^o = c- Then the boundary b(w, 0)

v^ould degenerate into a single point. In such cases, the normal vector at i/ = 0

may or may not be defined. To examine this in more detail, consider the tangents

of the isoparametric lines u = u^ evaluated at v = 0, These tangents must be

perpendicular to the normal vector, if it exists. So a condition for the existence

of the normal vector at c is that all z/-partials, evaluated at f = 0, are coplanar.

But that is equivalent to boi,

b^,...,

b^i and c being coplanar.

A second possibility in creating degenerate patches is to allov^ tw^o corner

partials to be coUinear, for example, d/du and d/dv at (0,0), as shov^n in Figure

14.13.

In that case, b^o^boi, and boo ^^^ coUinear. Then the normal at boo is

defined, provided that b^^ is not coUinear v^^ith bio?boi, and boo- Recall that

boo?bio?boi, and b^ form the osculating paraboloid at {u, v) = (0, 0). Then it

follow^s that the tangent plane at

boo

is the plane through the four coplanar points

boo?

bio? boi? and b^. The normal at boo is perpendicular to it.

A warning: when we say "the normal is defined," it should be understood that

this is a purely mathematical statement. In any of the preceding degeneracies,

a program using (14.17) will crash. A case distinction is necessary, and then

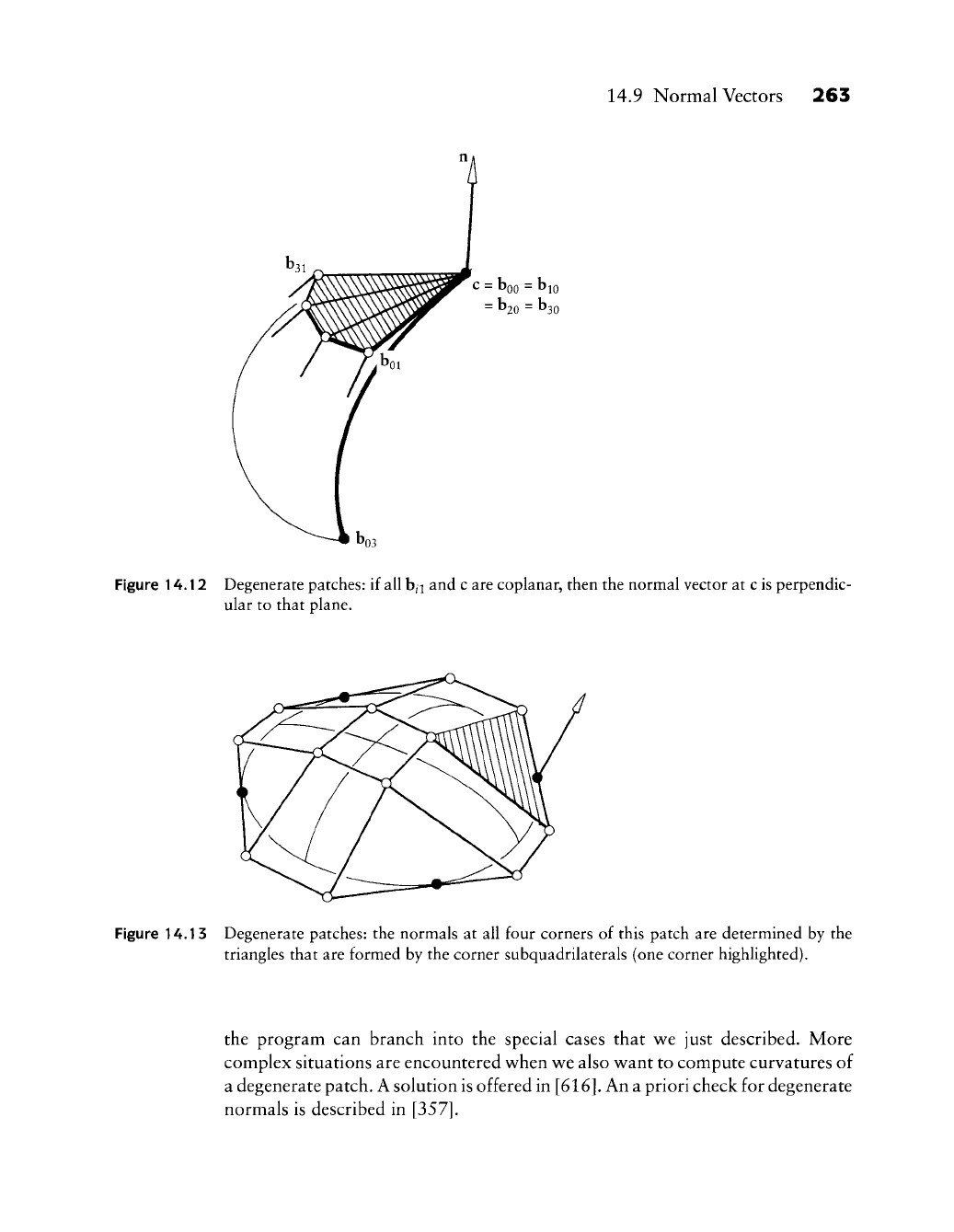
14.9 Normal Vectors 263

•

boo - bio

•

^20 = "30

Figure 14.12 Degenerate patches: if all h^ and c are coplanar, then the normal vector at c is perpendic-

ular to that plane.

Figure 14.13 Degenerate patches: the normals at all four corners of this patch are determined by the

triangles that are formed by the corner subquadrilaterals (one corner highlighted).

the program can branch into the special cases that we just described. More

complex situations are encountered when we also want to compute curvatures of

a degenerate patch. A solution is offered in

[616].

An a priori check for degenerate

normals is described in

[357].

264 Chapter 14 Tensor Product Patches

14.10 IWists

The twist of a surface^ is its mixed partial d^/dudv. According to (14.12), the

twist surface of

b'^'^

is a Bezier surface of degree (m

—

w —

1), and its (vector)

coefficients have the form mwA^'^b/y. These coefficients have a nice geometric

interpretation. The bihnear case is shown in Figure 14.14. In general, the point p/y

is the fourth point on the parallelogram defined by

b/+i

y_^i.

It is defined

Pw-bm,/=k;+l-kr (14.19)

Since

A^'^b,-,-

= (b,+i,,+i - b,+i,) - (b,-,,+i - b,,), (14.20)

it follows that

A''\, = b,+i,+i-p,-,. (14.21)

Thus the terms A^'^b^y measure the deviation of each subquadrilateral of the

Bezier net from a parallelogram.

The twists at the four patch corners determine the deviation of the respective

corner subquadrilaterals of the control net from parallelograms. For example,

dudv

b^'"(0,

0) = mwA^Xo- (14.22)

This twist vector is a measure for the deviation of b^ from the tangent plane at

boo-

An interesting class of surfaces is obtained if all subquadrilaterals

b^,y_^i,

b/+i,/9

b^_^i

y^i are parallelograms; in that case the twist vanishes everywhere. Such

surfaces are called translational surfaces and will be discussed in Section 15.3;

an example is shown in Figure 15.6. They have an interesting shape property: if

all control points of a translational surface lie on the boundary of their convex

hull, then the surface is convex; see Schelske

[540].

A surface is convex if it does

not contain a pair of points such that their connection by a straight line intersects

the surface.

4 In this chapter, we are dealing only with polynomial surfaces. For these, the twist is

uniquely defined. For other surfaces, it may depend on the order in which derivatives

are taken; see Section 22.6.

14.11 The Matrix Form of a Bezier Patch 265

Figure 14.14 Twists: the twist is proportional to the deviation of a control net quadrilateral from a

parallelogram.

14.11 The Matrix Form of a Bezier Patcii

In Section S.7^ we formulated a matrix expression for Bezier curves. This ap-

proach carries over v^ell to tensor product patches. We can write:

[B^{u) ... BZiu)]

boo

• • •

L D^Q . . . ^mn -I

(14.23)

The matrix

{b^;},

defining the control net, is sometimes called the geometry

matrix of the patch. If we perform a basis transformation and write the Bernstein

polynomials in monomial form, we obtain

rb,

b'^'^CM,

v)^[u^ ...

u'"]M^

bn„1 W^^

b^o

••

•

b„„J

f"J

(14.24)

The square matrices M and N are given by

'-<-"'-'(:)(:

(14.25)

and

«,/ = (-1>

,Mru'

//Vy

(14.26)

266 Chapter 14 Tensor Product Patches

In the bicubic case, m = n = 3^we have

M = N =

-3

-6

-1

-3

For reasons of numerical stabiUty, the use of the monomial form (14.24) is

not advisable (see the discussion in Section 24.3). It is included here since it is

still in widespread use.

14.12 Nonparametric Patches

This section is the bivariate analog of Section 6.5. Having outlined the main ideas

there, we can be brief here. A nonparametric surface is of the form z = f(x^ y).

It has the parametric representation

X(M, V) =

f{u, v) J

and we restrict both u and v to between zero and one. We are interested in

functions f that are in Bernstein form:

A^'3^)=EEMrw^F(y)-

I /

Using the identity (5.14) for both variables u and z/, we see that the Bezier points

are given by

i/m

jIn

The points (//m, j/n) in the x, y-plane are called Bezier abscissas of the function

f\ the bij are called its Bezier ordinates, A nonparametric Bezier function is not

constrained to be defined over the unit square; if a point p and two vectors v and

w define a parallelogram in the x, y-plane, then the Bezier abscissas a^y

E of a

nonparametric Bezier function over this domain are given by a/y = p + /v + /w.

Figure 14.15 gives an example.

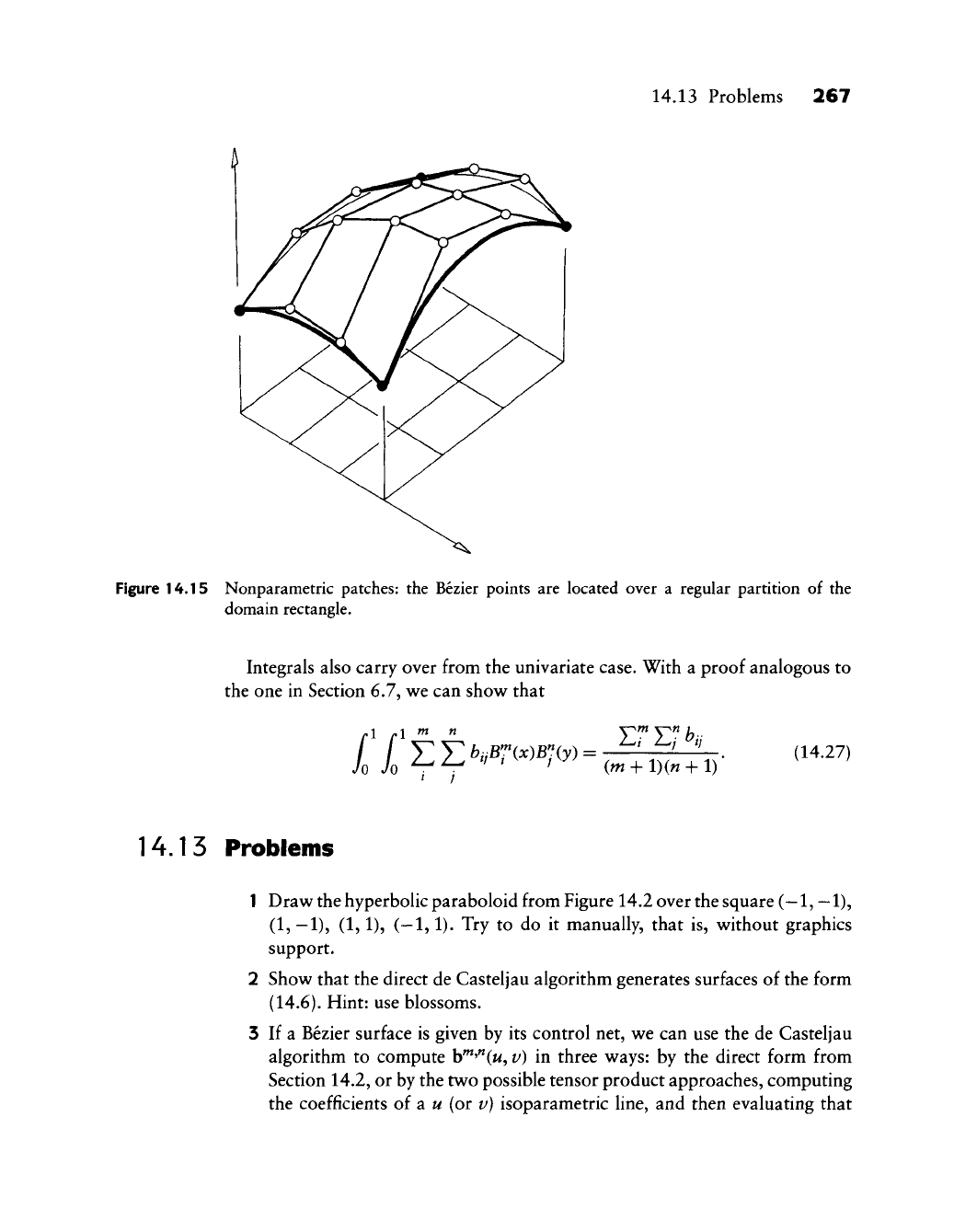
14.13 Problems 267

Figure 14.15 Nonparametric patches: the Bezier points are located over a regular partition of the

domain rectangle.

Integrals also carry over from the univariate case. With a proof analogous to

the one in Section 6.7, we can show that

-1 »i m n

y'"y"bii

I I TThB'"(x)B"(y)= ^' ^' " .

yo Jo Y /

+ l)(« + l)

(14.27)

14.15 Problems

1 Draw the hyperbolic paraboloid from Figure 14.2 over the square

(—1,

—1),

(1,

—1), (1,1), (—1,1). Try to do it manually, that is, without graphics

support.

2 Show that the direct de Casteljau algorithm generates surfaces of the form

(14.6).

Hint: use blossoms.

3 If a Bezier surface is given by its control net, we can use the de Casteljau

algorithm to compute b'^'^^Cw, v) in three ways: by the direct form from

Section 14.2, or by the two possible tensor product approaches, computing

the coefficients of a w (or v) isoparametric line, and then evaluating that

268 Chapter 14 Tensor Product Patches

curve at

(or

w).

Though theoretically equivalent, the computation counts

for these methods differ. Work out the details.

* 4 Show that Bezier surfaces have bilinear precision: if hjj = x(^, ^) and x is

bilinear, then b^'"(w, v) = x(w, v) for all

v and for arbitrary m, n,

* 5 Generalize (5.31) to the tensor product case.

PI Generalize the routine degree_e1 evate to the tensor product case.

P2 Generalize the routine ait ken to the tensor product case, that is, program

tensor product Lagrange interpolation.

P3 The data file car .dat contains data points (slightly modified) of four bound-

ary curves of one of the surfaces shov^n in Color Plate III. Try to fit a Bezier

patch (your pick of the degrees!) so that you get close to the corresponding

surface in the color plates.

Constructing

Polynomial Patches

We '

have discussed the underlying principles of polynomial patches; now it is

time to study how they can be used. First applications of tensor product patches

go back to General Motors, and Boeing in the United States, and to Renault and

Citroen in France.

15.1 Ruled Surfaces

One of the most elementary surface-building schemes is this: let two Bezier curves

h(u) and c(u) be given by their control polygons bo,

•

. ., b„ and

CQ,

.. ., c„, and

find a surface r(^, v) that connects them. The simplest such surface will use a

linear type of connection; it is called a ruled surface or lofted surface^ It is given

r(w, v) = (1

—

v)h(u)

-\-

vc{u).

(15.1)

For z/ = 0, it interpolates to b(w); for v—l^'\t interpolates to c{u).

The ruled surface r is linear in v and of degree n in u. In Bezier form, it becomes

r(w, v) = [1

— V

B"{u)

lB"„{u)A

1 The word lofted has an interesting history. In the days of completely manual ship design,

full-scale drawings were difficult to handle in the design office. These drawings were stored

and dealt with in large attics, called lofts.

269

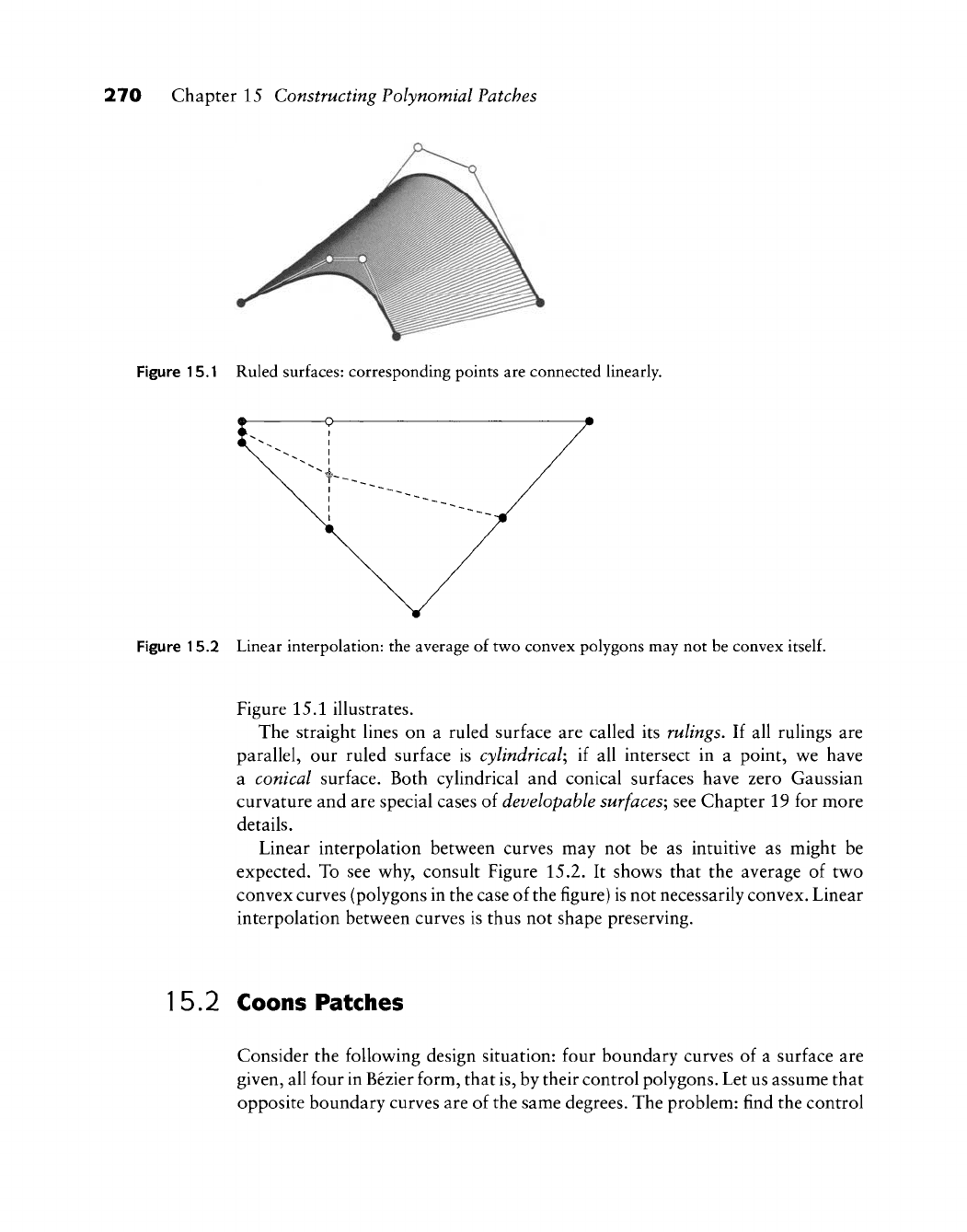
270 Chapter 15 Constructing Polynomial Patches

Figure 15.1 Ruled surfaces: corresponding points are connected linearly.

Figure 15.2 Linear interpolation: the average of two convex polygons may not be convex

itself.

Figure 15.1 illustrates.

The straight lines on a ruled surface are called its rulings. If all rulings are

parallel, our ruled surface is cylindrical; if all intersect in a point, we have

a conical surface. Both cylindrical and conical surfaces have zero Gaussian

curvature and are special cases of developable surfaces; see Chapter 19 for more

details.

Linear interpolation betw^een curves may not be as intuitive as might be

expected. To see v^hy, consult Figure 15.2. It show^s that the average of tw^o

convex curves (polygons in the case of the figure) is not necessarily convex. Linear

interpolation betv^een curves is thus not shape preserving.

15.2 Coons Patches

Consider the follov^ing design situation: four boundary curves of a surface are

given, all four in Bezier form, that

is,

by their control polygons. Let us assume that

opposite boundary curves are of the same degrees. The problem: find the control

15.2 Coons Patches 271

Figure 15.3 Coons patches: an example for

= 11 and m = 9.

net of a Bezier surface that fits between the boundary curves. This situation is

illustrated in Figure 15.3.

A configuration of the given data for m = n = 3 looks like this:

boo ^01 bo2 bo3

bio bi3

b20 b23

bso b3i b32 b33

The construction for the Coons surface mesh relies on the ruled surface form

Section 15.1 as well as the bilinear interpolant from Section 14.1. In order to

find the control point b/y, we first construct points on ruled surfaces:

and

bL =

(l-Mb,o

^,,«

We also need the point on the bilinear interpolant to the four corner points:

-•

•- n n

bo,o bo,^

bw,0 ^m,n

1-zr.

m -J

The desired control point is found as a combination of these three points:

hi=h,,+h,rhf

(15-2)

Figure 15.4 illustrates the construction method. Figure 15.5 gives an example

of a completed control net.

Coons patches were originally defined in a more general setting, see Chapter

22.

Since the Coons technique in this section only deals with piecewise linear