Farin G. Curves and Surfaces for CAGD. A Practical Guide

Подождите немного. Документ загружается.

232 Chapter 13 Rational Bezier and B-Spline Curves

Figure 13.3 Convex hulls: if the weight points are used, tighter bounds on the curve are possible.

parameters: moving a q^ along the polygon leg

b/,

b^_^i

influences the shape of the

curve. It may be preferable to let a designer use these geometric handles rather

than requiring him or her to input numbers for the v^eights.^

As in the nonrational case, the de Casteljau algorithm may be used to subdi-

vide a curve. The de Casteljau algorithm subdivides the 4D preimage of our

3D rational Bezier curve x(^); see Section 5.4. The intermediate 4D points

[w/[b[ w^-Yy b^ e E^, may be projected into the hyperplane w=lto provide us

v^ith the control polygons for the "left" and "right" curve segment. The control

vertices and w^eights corresponding to the interval [0, t] are given by

hf' =

h',(t),

wf'^w'^,

(13.5)

w^here the bQ(^) and the

art computed from (13.3). The control points and

w^eights corresponding to the interval [t, 1] are given by

hf^^' =

h';-'it),

u/^ =

u/l-'.

(13.6)

The w^eight points may be used to sharpen the convex hull property of rational

Bezier curves. We know^ that every curve is inside the convex hull of its control

polygon. But it is also contained w^ithin the convex hull of bo, qo,. .., q^-i? b„;

see

[201].

Figure 13.3 illustrates.

5 This situation is similar to the way curves are generated using the direct G^ spline

algorithm from Chapter 11 compared to the generation of y splines.

13.3 Derivatives 233

15.3 Derivatives

For the first derivative of a rational Bezier curve, we obtain

x{t) = ^[p(t) - wit)x(t)l

wit)

(13.7)

where we have set

p(0 = w(t)xit); pit), xit) e E^

(13.8)

in complete analogy to the development in Section 12.4. For higher derivatives,

we differentiate (13.8) r times:

p^'\t)

= J2(j]w^\t)x^'-^\t),

We can solve for

x^^\t):

x^'\t)

wit)

^(r)

-go

w^\t)x^''-'\t)

(13.9)

This is a recursive formula for the rth derivative of a rational Bezier curve. It only

involves taking derivatives of polynomial curves.

The first derivative may also be obtained as a byproduct of the de Casteljau

algorithm, as described by Floater

[235]:

w^'-^w'!-^ 1 1

^it) = n—p-^;^;—[bj -bQ J.

(13.10)

At the endpoint

= 0, we find

Let us now consider two rational Bezier curves, one defined over the interval

[WQ?

^i] with control polygon bo,..., b„ and weights

W/Q?

•.., t^„ and the other

defined over the interval [t/j, uj] with control polygon b„,... ,b2„ and weights

w/„,...,

Win. ^oxh segments form a C^ curve if

!f:^Ab„_i=^^^Ab„

(13.11)

234 Chapter 13 Rational Bezier and B-Spline Curves

where the appearance of the interval lengths A^ is due to the application of the

chain rule. This is necessary since we now consider a composite curve with a

global parameter u. Note that the weight w^ has no influence on differentiability

at all!

Of course, two rational Bezier curves form a C^ curve if all of their components

are C^ in homogeneous form:

A'[w^.rK-r]

A'lWnK]

(Ao)^

(Air

But keep in mind that there are composite C^ curves that do not satisfy this

condition!

Although the computation of higher-order derivatives is quite involved in the

case of rational Bezier curves, we note that the computation of curvature or

torsion may be simplified by the application of (10.9) or (10.10) and (10.11).

15.4 Oscuiatory Interpolation

With rational cubics, it is easy to solve an interesting kind of interpolation

problem: given a Bezier polygon bo, b^, b2, b3 and a curvature value at each

endpoint, find a set of weights

U/Q,

^i, wi, w^ such that the corresponding rational

cubic assumes the given curvatures at bg and b3. The following method is very

similar to one developed by T. Goodman in 1988; see

[271].

We assume without

loss of generality that

= W^ = 1.^ The given curvatures

and K^ are then

related to the unknown weights by (10.10):

KQ:

4W2

^3-

4wi

w?;

--j"^'

(13.12)

where

CQ:

area[bQ,bi,b2]

dist^[bo,bi]

Ci =

area[bi,b2,b3]

dist^[b2,b3]

Equations (13.12) decouple nicely so that we can determine our unknowns ivi

and Wi:

tv,--

fo£i

U.2=-

fofi

(13.13)

6 Goodman [271] assumes that

M'2

= 1.

13.5 Reparametrization and Degree Elevation 235

Figure 13.4 Reparametrizations: three rational Bezier curves with identical control polygons, evalu-

ated at 31 equally spaced parameter values. Reparametrization constants are top, c = 2;

middle, c = l; bottom, c = 1/2.

For planar control polygons, the quantities

or Ci may be negative—this

happens when a control polygon is S-shaped. This is meaningful since curvature

may be defined as signed curvature for 2D curves, as defined in (23.1). Of course,

we should then also prescribe the corresponding

and

/C3

as being negative so

that we end up with positive weights.

A similar interpolation problem was addressed by Klass [361] and de Boor,

HoUig, and Sabin for the nonrational case: they prescribe two points and corre-

sponding tangent directions and curvatures

[144].

The solution (when it exists)

can only be obtained using an iterative method.

15.5 Reparametrization and Degree Elevation

Arguing exactly as in the conic case (see the end of Section 12.2), we may

reparametrize a rational Bezier curve by changing the weights according to

Wi = c^Wj; / = 0,..., w.

where c is any nonzero constant. Figure 13.4 shows how the reparametrization

affects the parameter spacing on the curve; note that the curve shape remains the

same.

The new weights correspond to new weight points q^. One can show (see

Farin and Worsey [216]) that the new and old weight points are strongly related:

236 Chapter 13 Rational Bezier and B-Spline Curves

the cross ratios of any four points

[b^,

q^, q^, b/+i] are the same for all polygon

legs.

We may always transform a rational Bezier curve to standard form by using

the rational linear parameter transformation resulting from the choice

c =

This results in w^ =

WQ;

after dividing all weights through by

WQ^

we have the

standard form

= W^ = 1. Of course, we have to require that the root exists.

A different derivation of this result is in Patterson

[457].

How can rational Bezier curves in nonstandard form arise? A common case

occurs in connection with rational Bezier surfaces, as discussed in Section 16.6:

the end weights of an isoparametric curve will in general not be unity. Such

curves are often "extracted" from a surface and then treated as entities in their

own right.

We may perform degree elevation (in analogy to Section 6.1) by degree el-

evating the 4D polygon with control vertices

[

w^i w^ ]^ and projecting the

resulting control vertices into the hyperplane w=\. Let us denote the control

vertices of the degree elevated curve

hf; they are given by

b-'

= • —; / =

0,...,«

+ l (13.14)

and a I = i/{n + 1). The weights w- of the new control vertices are given by

w^ = Wi_iai -f- Wi{l

—

Qf^); / =

0,...,«

+ 1.

Degree elevation is illustrated in Example 13.1.

The connection of reparametrization and degree elevation may lead to surpris-

ing situations. Consider the following procedure: take any rational Bezier curve in

standard form and degree elevate it. Next, take the original curve, reparametrize

it, then degree elevate it and bring it to standard form. We end up with two differ-

ent polygons (and two different sets of standardized weights) that both describe

the same rational curve. This situation is very different from the nonrational case!

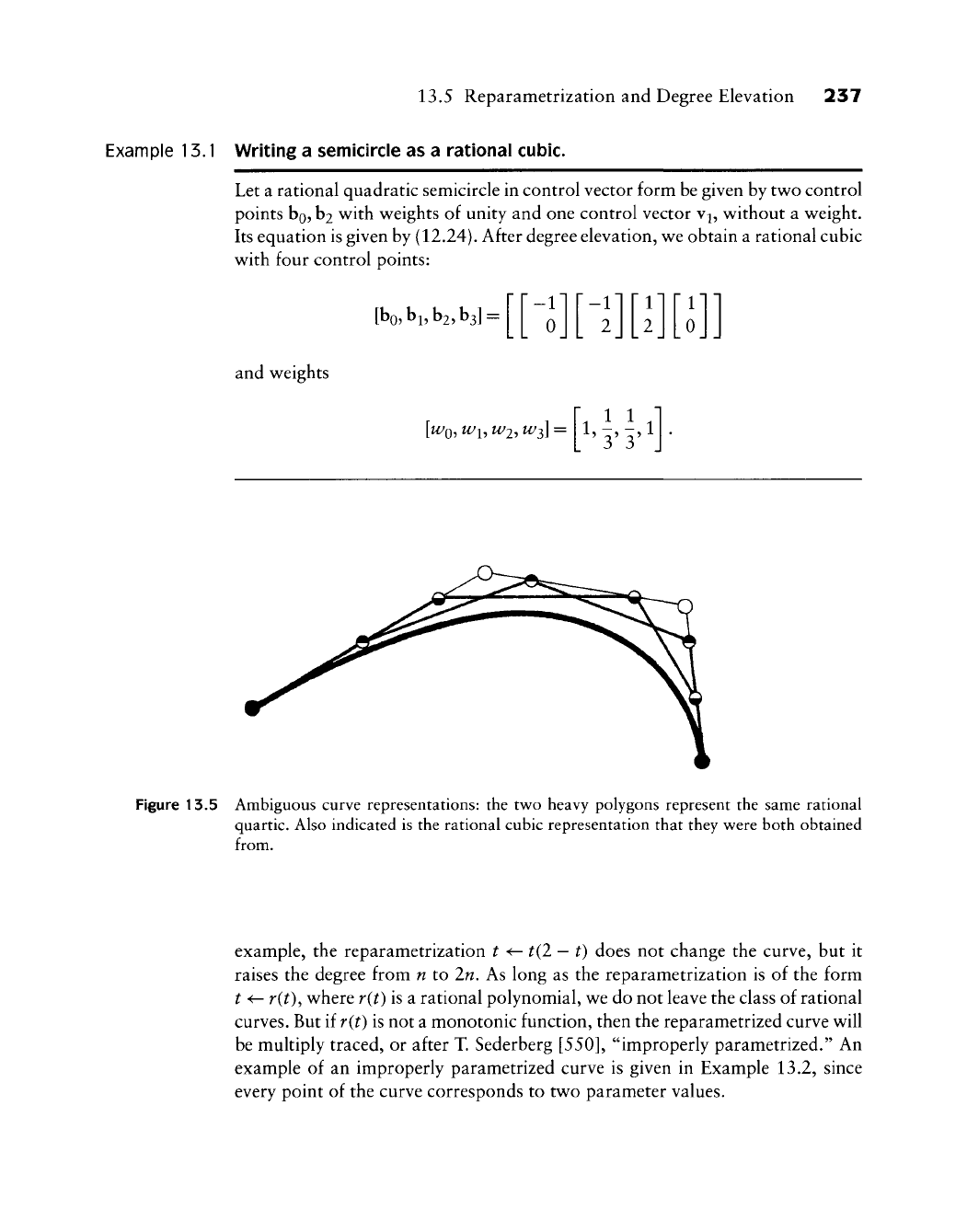
It is illustrated in Figure 13.5.

For the sake of completeness, we should mention that ways other than just

by rational linear reparametrizations exist to reparametrize rational curves. For

13.5 Reparametrization and Degree Elevation 237

Example 13.1 Writing a semicircle as a rational cubic.

Let a rational quadratic semicircle in control vector form be given by two control

points bo, hi with weights of unity and one control vector v^, without a weight.

Its equation is given by (12.24). After degree elevation, we obtain a rational cubic

with four control points:

[bo,

bi,

b2,

b3]:

-11

r-1]

121

and weights

[WQ, tVi, W2, W^] =

Figure 13.5 Ambiguous curve representations: the two heavy polygons represent the same rational

quartic. Also indicated is the rational cubic representation that they were both obtained

from.

example, the reparametrization t <-t(2

—

t) does not change the curve, but it

raises the degree from n to In, As long as the reparametrization is of the form

t <- r{t), where r(t) is a rational polynomial, we do not leave the class of rational

curves. But if r(t) is not a monotonic function, then the reparametrized curve will

be multiply traced, or after T. Sederberg

[550],

"improperly parametrized." An

example of an improperly parametrized curve is given in Example 13.2, since

every point of the curve corresponds to two parameter values.

238 Chapter 13 Rational Bezier and B-Spline Curves

Example 13.2 Writing a full circle as a rational quintic.

It is possible to write a full circle as one rational Bezier curve of degree five (see

Chou [114]). Its Bezier points are given by

"1]

ri]

[-3]

[-2

r ii

[-4

and its weights are

'1111;

'5'5'5'5'

As the parameter t traces out all values betv^een —00 and +00, the circle is traced

out tv^ice.

15.6 Control Vectors

In Section 12.8, v^e encountered control vectors (also known as infinite control

points) as the limiting case of parallel tangents to a conic. The resulting curve

representation contained both points and vectors. We can devise a similar form

for rational Bezier curves, first suggested by K. Versprille

[601];

see also

[477].

They will be of the form

Ht)

^points

^.M^O + EvectorsV.^?W

Epomts^.^?(0

(13.15)

The control vectors do not have weights in this form; we may multiply each v^

by a factor, however, and the curve will change accordingly. Note that at least

one of the point weights Wj must be nonzero for (13.15) to be meaningful.

As in the conic case, we have lost the convex hull property, and evaluation

of (13.15) will require special case treatment. However, we can eliminate the

control vectors completely—we just have to degree elevate the curve (possibly

more than once). Example 13.1 shows how to do this.

15.7 Rational Cubic B-Spline Curves

A 3D rational B-spline curve is the projection through the origin of a 4D non-

rational B-spline curve into the hyperplane w = 1. The control polygon of the

13.7 Rational Cubic B-Spline Curves 239

Figure 13.6 Rational B-splines: the weight of the indicated control point is changed. Dashed curve,

weight

3.0; black curve, weight

0.33.

rational B-spline curve is given by vertices do,..., d^^; each vertex d/ € E^ has a

corresponding weight Wi, A point x(w) on a rational B-spline curve is thus given

x(w) =

(13.16)

It may be evaluated by applying the de Boor algorithm (see Section 8.2), to

the homogeneous coordinates, in the same way as we evaluated rational Bezier

curves. We have affine and projective invariance, and also the local control

property. For nonnegative weights, we have the variation diminishing property

as well as the convex hull property.

Designing with rational B-spline curves is not very different from designing

with their nonrational counterparts. We now have the added freedom of being

able to change weights. A change of only one weight affects a rational B-spline

curve only locally, as shown in Figure 13.6.

Let us close this section with a somewhat negative result: there is no symmetric

periodic representation of

circle as a C^ rational cubic B-spline curve. If such

a representation existed, it would be of the form

x(^) = Y, w,d,Nf(u)/ J2

^tN^u),

where all

art equal by symmetry. Then the

cancel, leaving us with an integral

B-spline curve, which is not capable of representing a circle. Note, however, that

we can represent any open circular arc by C^ rational cubics.

240 Chapter 13 Rational Bezier and B-Spline Curves

5.8 Interpolation with Rational Cubics

The interpolation problem in the context of rational B-splines is the following:

Given: 3D data points

XQ,

...,

x^^,

parameter values

UQ,

...,

uj^^

and weights

Find:

A C^ rational cubic B-spline curve with control vertices do,..., d^+i

and weights f

• • • ?

^K+l ^hat interpolates to the given data and weights.

For the solution of this problem, we follow the philosophy outlined at the

end of the last section: solve a 4D interpolation problem to the data points

[

w-Ki

]^ and parameter values W/. All we have to do is to solve the linear

system (9.10), where input and output is now 4D instead of the usual 3D. We

will obtain a 4D control polygon [

] , from which we now obtain the

desired d^ as d^ = ^i/Vv The

are the weights of the control vertices d^.

We have not yet addressed the problem of how to choose the weights Wi

for the data points x^. No known algorithms exist for this problem. It seems

reasonable to assign high weights in regions where the interpolant is expected

to curve sharply. Yet there is a limit to the assignment of weights: if all of them

are very high, this will not have a significant effect on the curve since a common

factor in all weights will simply cancel. Moreover, care must be taken to prevent

the denominator of the interpolant from being zero. This is not a trivial task—

for instance, we might assign a very large weight to one data point while keeping

all the others at unity. The resulting weight function w{t) will not be positive

everywhere, giving rise to singularities at its zeros.

Integral cubic spline interpolation has cubic precision: if the data points and

the parameter values come from one global cubic, the interpolant reproduces

that cubic. In the context of rational spline interpolation, an analogous question

is that of conic precision: if the data points and the parameter values come from

one global conic, can we reproduce it? We must also require that the data points

have weights assigned to them. With them, we may view the rational spline

interpolation problem as an integral spline interpolation problem in E"^. There,

cubic splines have quadratic precision; that is, we may recapture any parabola.

The projection of the parabola yields a conic section; thus if our data—points,

parameter values, and weights—were taken from a conic, rational cubic spline

interpolation will reproduce the conic.

We should note, however, that this argument is limited to open curves; for

closed curves, we have already seen that we cannot represent a circle as a C^

symmetric periodic B-spline curve.

More approaches to rational sphne interpolation have recently appeared; we

hst Schneider [541] and Ma and Kruth

[408].

13.9 Rational B-Splines of Arbitrary Degree 241

13.9 Rational B-Splines of Arbitrary Degree

The process of generalizing the concept of general B-spline curves to the rational

case is now straightforward. A 3D rational B-spline curve is the projection

through the origin of a 4D nonrational B-spline curve into the hyperplane w=l.

It is thus given by

^M^^ • (13-17)

We have chosen the notation from Chapter 8. Thus (13.17) is the generalization

of (8.15) to the rational parametric case.

A rational B-spline curve is given by its knot sequence, its 3D control polygon,

and its weight sequence. The control vertices dj art the projections of the 4D

control vertices

[

Wjdi

]^.

To evaluate a rational B-spline curve at a parameter value w, we may apply

the de Boor algorithm to both numerator and denominator of (13.17) and finally

divide through. This corresponds to the evaluation of the 4D nonrational curve

with control vertices

[

Wjdj

]^ and to projecting the result into

E-^.

Just as in

the case of Bezier curves, this may lead to instabilities, and so we give a rational

version of the de Boor algorithm that is more stable but also computationally

more involved.

de Boor algorithm, rational: Let u e [uj, uj^i) c [w„_i, uj}. Define

d^{u) = [a - af)wf:ldf:l(u) + afwf-^df-\u)]/wf (13.18)

for ^ = 1,. ..,

w —

r, and / = I

— w

+ ^ + 1,.. ., / + 1, where

k ^ - ^i-i

"-i-^-n-k ^i-1

and

Then

wf = il-af)wf:l +

afwf-

siu) = d'^-[(u) (13.19)

is the point on the B-spline curve at parameter value u. Here, r denotes the

multiplicity of u in case it was already one of the knots. If it was not, set r = 0.

As usual, we set d^ = dj and w^ = Wj.

Refer to Section 8.3 for the notation.