Farin G. Curves and Surfaces for CAGD. A Practical Guide

Подождите немного. Документ загружается.

242 Chapter 13 Rational Bezier and B-Spline Curves

Knot insertion is, as in the nonrational case, performed by executing just one

step of the de Boor algorithm, that is, by fixing ^ = 1 in the preceding algorithm.

The original polygon vertices d/_„_^25

•

• •

d/ are replaced by the

dj_^, 2?

•

• •

^ilv

their weights are the numbers Wj_^^2^..., Wj^^

A rational B-spline curve, being a piecewise rational polynomial, has a piece-

wise rational Bezier representation. We can find the Bezier points and their

weights for each segment by inserting every knot until it has multiplicity «, that

is,

by applying the de Boor algorithm to each knot. The routine bsptobez_bl ossom

uses blossoms to perform this task.

It is also possible to reparametrize a rational B-spline curve, just as we could

do for Bezier curves. For a description, see Lee and Lucian

[381].

The derivative of a rational B-spline curve is conveniently found using a result

by Floater:

s{u)

= —^ !^L^[d«;i -

d«-i],

(13.20)

which is quite analogous to (13.10).

15.10 Implementation

The following computes a point on a rational Bezier curve:

float ratbez(degree,coeff.weight.t)

uses rational

caste!jau

compute

point

ratbez curve for param. value

Input: degree: degree

curve

coeff: control point coordinates

weight: weights

t: evaluation parameter

Reparametrizing a rational Bezier curve:

void reparam(wold,degree,s,wnew)

reparametrizes ratbez curve: only the weights, stored

wold,

are changed. New weights are in wnew. Parametrization

determined

shoulder point s. For s=0.5, nothing changes.

Also,

should

be in

(0,1).

13.11 Problems 243

The routine to subdivide a rational Bezier curve at a parameter value t was

already given in Section 5.8.

A program that generates the piecew^ise rational Bezier form from a rational

cubic B-spline curve is:

void ratbspline_to_bezier(bsp1_x,bspl_y,bspl_w,knot,l,bez_x,bez_y,bez_w)

/* converts rational cubic B-spline polygon into piecewise

rational Bezier polygon

Input: bspl_x, bspl_y: planar B-spline control polygon

bspl_w: B-spline weights

knot: knot sequence

1: no.

intervals

Output: bez_x, bez_y: planar piecewise Bezier polygon

bez_w: Bezier weights (not

piecewise standard form!)

5.11 Problems

1 Suppose you are given two coplanar rational quadratic segments that form

a C^ curve, but not a G^ curve. Can you adjust the weights (not the control

polygons!) such that the resulting new segments form a G^ curve? Hint: use

(10.9).

* 2 A rational Bezier curve may be

closed^

as in the example of a degree elevated

ellipse. Show that a nonplanar 3D rational cubic cannot be closed.

* 3 In Section 13.4, we said that signed curvature makes sense only in e. Why

not in ¥?}

*4 In Section 13.5, we remarked that the cross ratios of any four points

(b/,

q^, q^, b/_^i) are the same for all polygon legs. How is this cross ratio

related to the reparametrization constant c?

PI Define and program a rational Aitken algorithm, that is, one where the

data points are assigned weights. Try to adjust those weights in an attempt

to reduce the oscillatory behavior of the interpolant.

P2 Use deboor_blossom to write a degree elevation program for rational B-

splines. Apply it repeatedly and study the behavior of the weights.

This Page Intentionally Left Blank

Tensor Product

Patches

I he first person to consider this class of surfaces for design purposes was

probably de Casteljau, who investigated them between 1959 and 1963. The

popularity of this type of surface is, however, due to the work of Bezier only

slightly later, as documented in Chapter 1. Initially, Bezier patches were only

used to approximate a given surface. It took some time for people to realize that

any B-spline surface can also be written in piecewise Bezier form.

We will use the example of Bezier patches to demonstrate the tensor product

approach to surface patches. Once that principle is developed, it will be trivial

to generalize other curve schemes to tensor product surfaces.

14.1 Bilinear Interpolation

In Section

3.1,

we studied linear interpolation in E^ and derived properties of this

elementary method that we then used for the development of Bezier curves. In

an analogous fashion, we can base the theory of tensor product Bezier surfaces

on the concept of bilinear interpolation. Whereas linear interpolation fits the

"simplest" curve between two points, bilinear interpolation fits the "simplest"

surface between four points.

To be more precise: let

bo^o? ^0,1?

be four distinct points in E^. The set

of all points x

E^ of the form

1 1

/=0 /=0

(14.1)

245

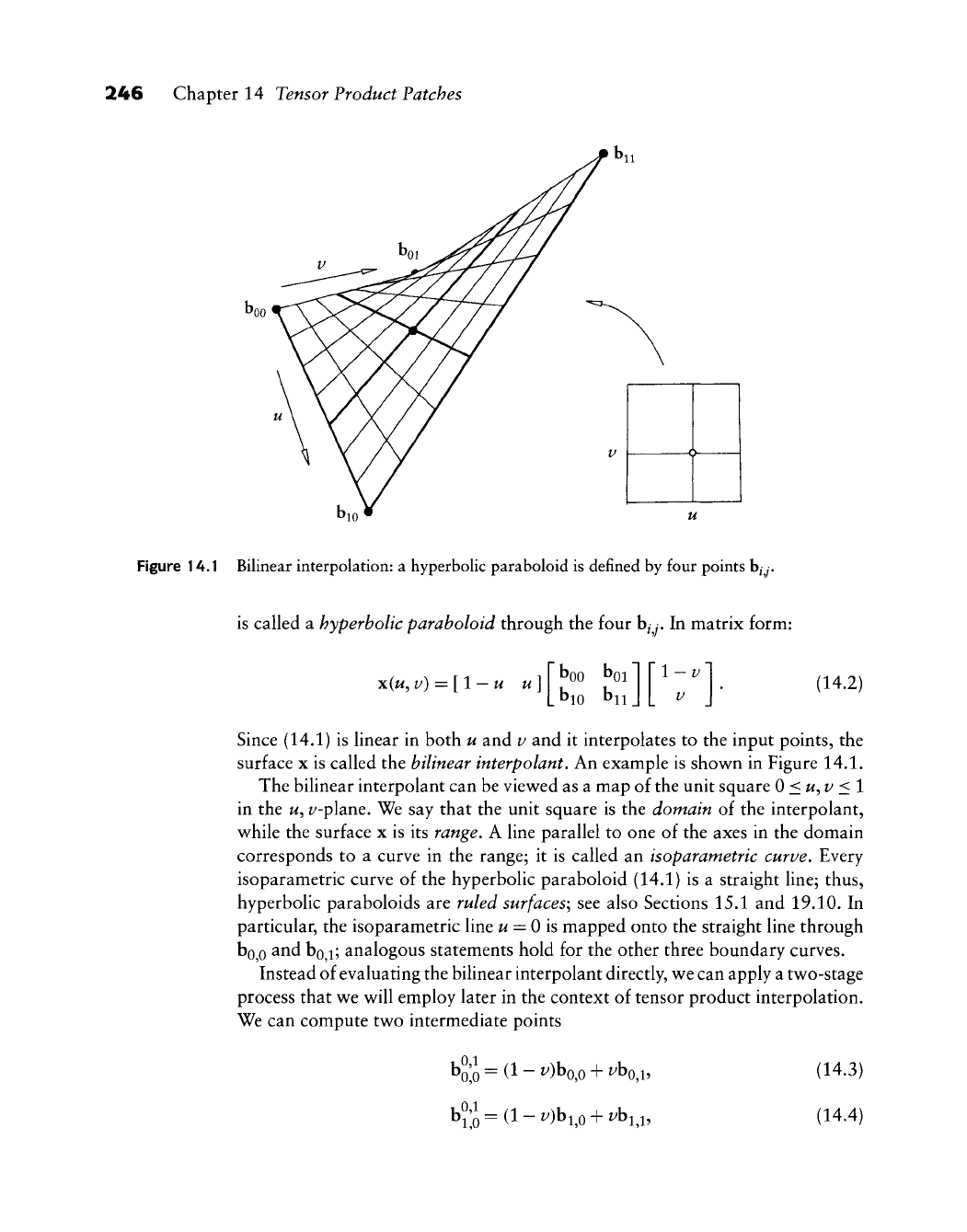
246 Chapter 14 Tensor Product Patches

-0

Figure 14.1 Bilinear interpolation: a hyperbolic paraboloid is defined by four points b^y.

is called a hyperbolic paraboloid through the four hjj. In matrix form:

x(w, v) = [l

—

u u]

boo boi

bio bii

1-v

(14.2)

Since (14.1) is linear in both u and v and it interpolates to the input points, the

surface x is called the bilinear interpolant. An example is shown in Figure 14.1.

The bilinear interpolant can be viewed as a map of the unit square 0<u^v <l

in the u, i^-plane. We say that the unit square is the domain of the interpolant,

while the surface x is its range. A line parallel to one of the axes in the domain

corresponds to a curve in the range; it is called an isoparametric curve. Every

isoparametric curve of the hyperbolic paraboloid (14.1) is a straight line; thus,

hyperbolic paraboloids are ruled

surfaces-^

see also Sections 15.1 and 19.10. In

particular, the isoparametric line

= 0 is mapped onto the straight line through

^nd bo i; analogous statements hold for the other three boundary curves.

Instead of evaluating the bilinear interpolant directly, we can apply a two-stage

process that we will employ later in the context of tensor product interpolation.

We can compute two intermediate points

0,1

\o = (1 - ^)bo,o + ^bo,i.

0.1

bi;o = (1 - ^)bi,o + ^bi4.

(14.3)

(14.4)

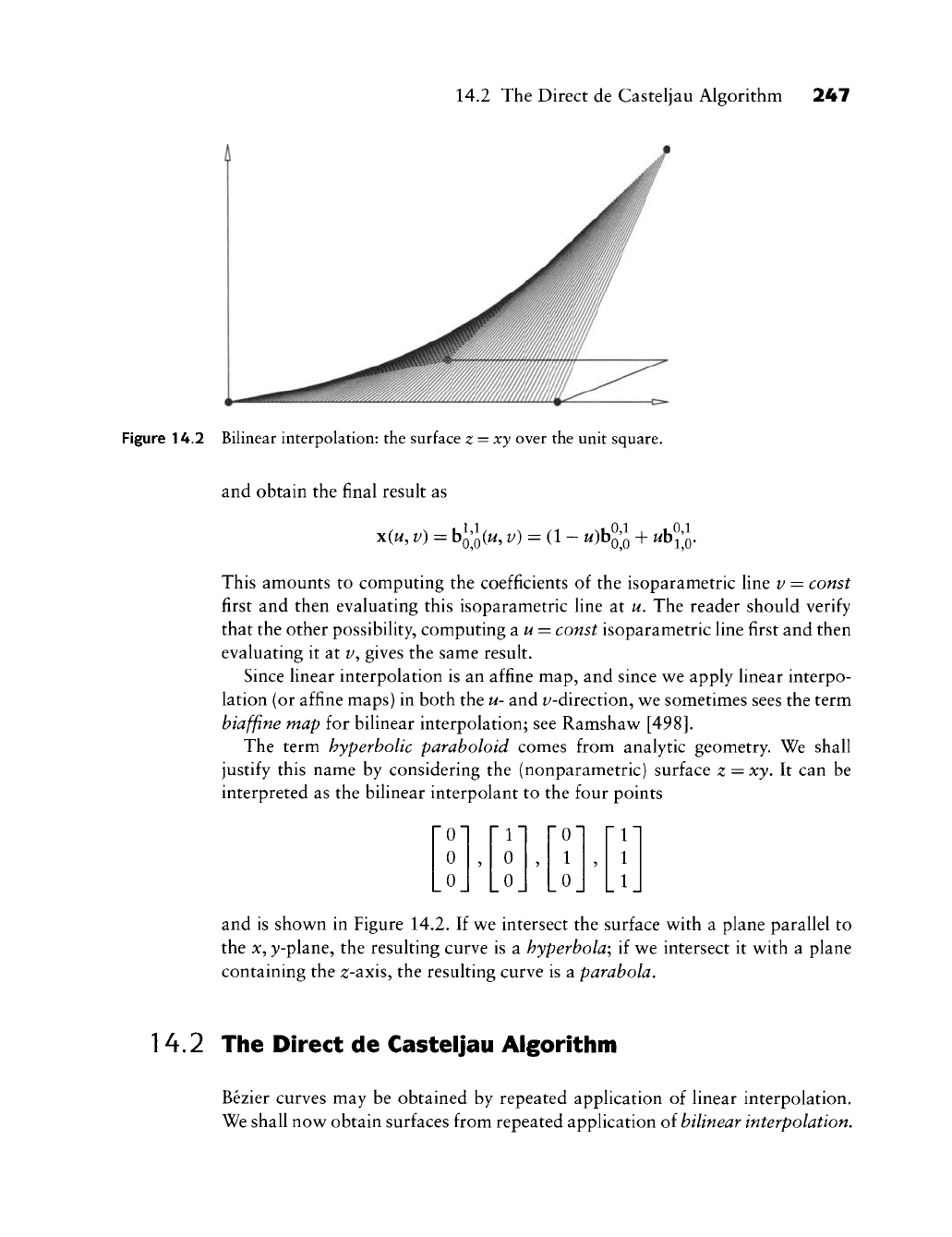
14.2 The Direct de Casteljau Algorithm 247

Figure 14.2 Bilinear interpolation: the surface z = xy over the unit square.

and obtain the final result as

x(w, v) = h^^^iu, v) = {l- u)h^^Q + wb^^Q.

This amounts to computing the coefficients of the isoparametric line v = const

first and then evaluating this isoparametric line at u. The reader should verify

that the other possibility, computing au = const isoparametric line first and then

evaluating it at v, gives the same result.

Since linear interpolation is an affine map, and since v^e apply linear interpo-

lation (or affine maps) in both the u- and ^/-direction, v^e sometimes sees the term

biaffine map for bilinear interpolation; see Ramshaw^

[498].

The term hyperbolic paraboloid comes from analytic geometry. We shall

justify this name by considering the (nonparametric) surface z = xy. It can be

interpreted as the bilinear interpolant to the four points

and is show^n in Figure 14.2. If wt intersect the surface v^ith a plane parallel to

the

}/-plane, the resulting curve is a hyperbola; if we intersect it w^ith a plane

containing the ^-axis, the resulting curve is a parabola.

4.2 The Direct de Casteljau Algorithm

Bezier curves may be obtained by repeated application of linear interpolation.

We shall now^ obtain surfaces from repeated application of bilinear interpolation.

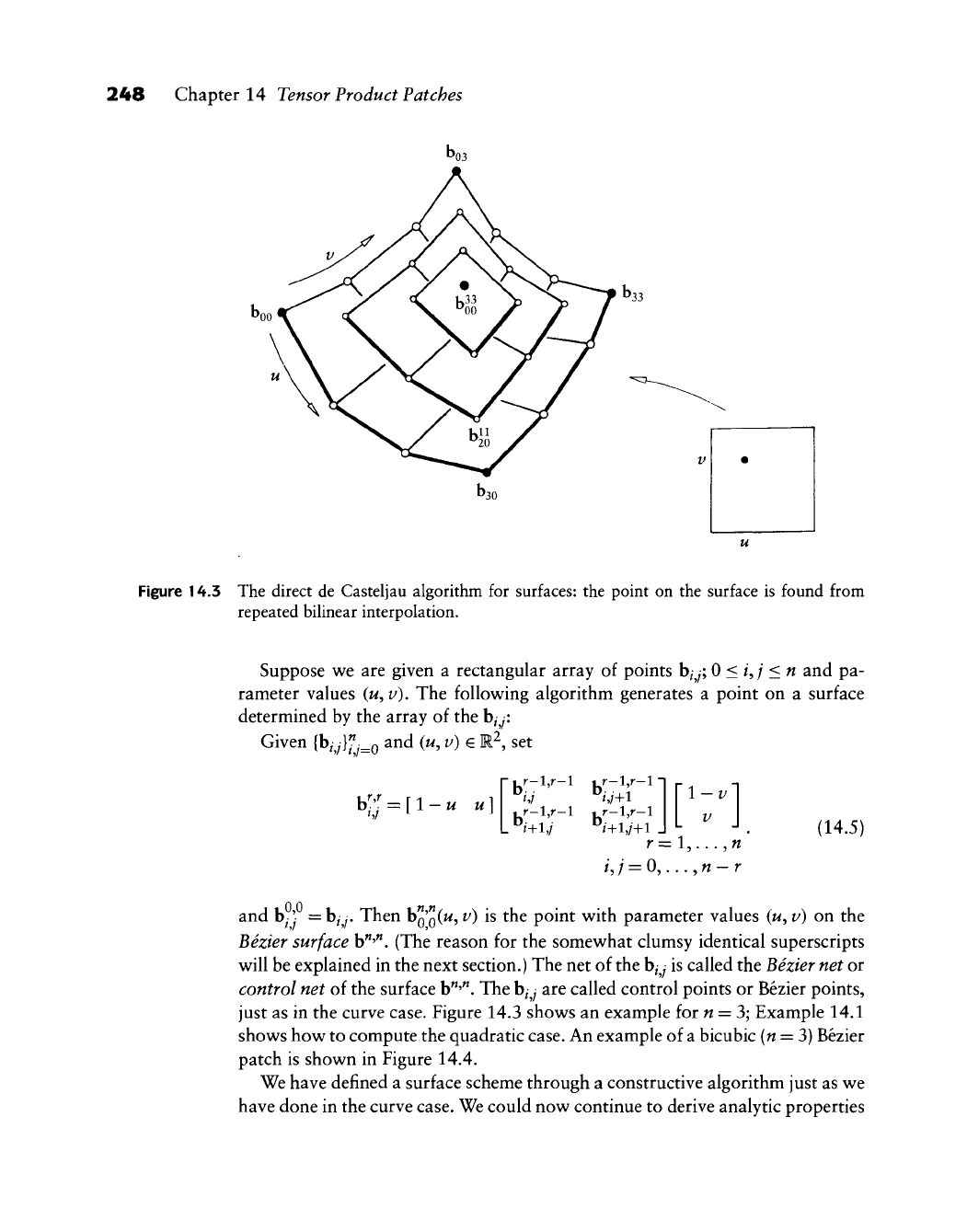
248 Chapter 14 Tensor Product Patches

Figure 14.3 The direct de Casteljau algorithm for surfaces: the point on the surface is found from

repeated biUnear interpolation.

Suppose we are given a rectangular array of points

0 <ij <n and pa-

rameter values

(M,

V). The following algorithm generates a point on a surface

determined by the array of the hjji

Given

{b^^}"-

and (w, v) e M^, set

h'j=[l-u u]

1 r-l,r-l

,r-l,r-l

1-V

r=l,...,«

ij =

0,...,n-r

(14.5)

and b-' =

b^y.

Then h^'^iu^ v) is the point with parameter values (w, v) on the

Bezier surface h^'^, (The reason for the somewhat clumsy identical superscripts

will be explained in the next section.) The net of the hjj is called the Bezier net or

control net of the surface

b"'".

The

are called control points or Bezier points,

just as in the curve case. Figure 14.3 shows an example for n = 3; Example 14.1

shows how to compute the quadratic case. An example of a bicubic (n = 3) Bezier

patch is shown in Figure 14.4.

We have defined a surface scheme through a constructive algorithm just as we

have done in the curve case. We could now continue to derive analytic properties

14.2 The Direct de Casteljau Algorithm 249

Example 14.1 Computing a point on a Bezier surface using the direct de Casteljau algo-

rithm.

Let a Bezier control net be given by

After one step of the direct de Casteljau algorithm for (w, v) = (0.5, 0.5), we

obtain

["11

ri'

[31

0.5

" 3 "

2.5

The point on the surface is

of these surfaces, again as in the curve case. This is possible w^ithout much effort;

how^ever, we use a different approach in Section 14.3.

In the next section, v^e shall be able to handle surfaces that are of different

degrees in u and v. Such surfaces have control nets

{hjj};

/ = 0,..., m,/ =

0,...,

The direct de Casteljau algorithm for such surfaces exists, but it needs

a case distinction: consulting Figure 14.5, v^e see that the direct de Casteljau

algorithm cannot be performed until the point of the surface is reached. Instead,

after k = min(m,«), the intermediate b-' form a curve control polygon. We now^

must proceed with the univariate de Casteljau algorithm to obtain a point on

the surface. This case distinction is awkward and will not be encountered by the

tensor product approach in the next section.

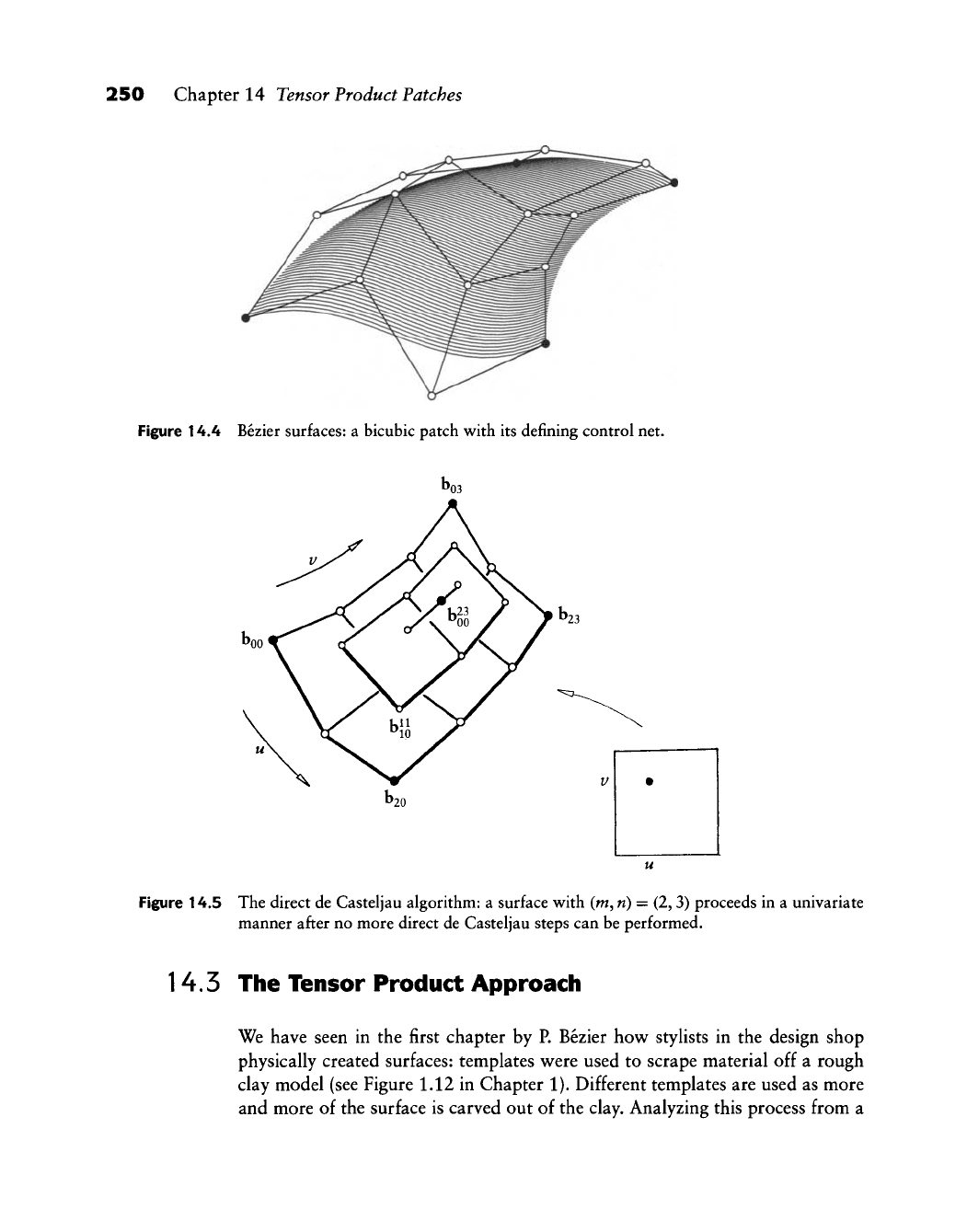
250 Chapter 14 Tensor Product Patches

Figure 14.4 Bezier surfaces: a bicubic patch with its defining control net.

Figure 14.5 The direct de Casteljau algorithm: a surface with

(m,

= (2,3) proceeds in a univariate

manner after no more direct de Casteljau steps can be performed.

14.5 The Tensor Product Approach

We have seen in the first chapter by P. Bezier how stylists in the design shop

physically created surfaces: templates were used to scrape material off a rough

clay model (see Figure 1.12 in Chapter 1). Different templates are used as more

and more of the surface is carved out of the clay. Analyzing this process from a

14.3 The Tensor Product Approach

251

Figure 14.6 Tensor product surfaces: a surface can be thought of as being swept out by a moving and

deforming curve.

theoretical viewpoint, we arrive at the following intuitive definition of a surface: a

surface is the locus of a curve that is moving through space and thereby changing

its shape. See Figure 14.6 for an illustration.

We will now formalize this intuitive concept in order to arrive at a mathemat-

ical description of a surface. First, we assume that the moving curve is

Bezier

curve of constant degree m. (This assumption is made so that the following for-

mulas will work out; it is actually a serious restriction on the class of surfaces that

we can represent using the tensor product approach.) At any time, the moving

curve is then determined by a set of control points. Each original control point

moves through space on a curve. Our next assumption is that this curve is also

a Bezier curve, and that the curves on which the control points move are all of

the same degree. An example is given in Figure 14.7.

This can be formalized as follows: let the initial curve be

Bezier curve of

degree m:

b-(^)

^b,Br(^).

^=0

Let each

traverse a Bezier curve of degree n:

j=0

We can now combine these two equations and obtain the point h^'^{u, v) on

the surface b^'^ as

{T'^iu,

v) =

Y,Y. Mr(«)^"(^)-

(14-6)

!=0 /=0