Farin G. Curves and Surfaces for CAGD. A Practical Guide
Подождите немного. Документ загружается.


222 Chapter 12 Conic Sections
Figure 12.11 Circles: a whole circle may be written as three rational Bezier quadratics.
form an isosceles triangle. If we know the angle a = Z(b2, bo,
b^),
we should be
able to determine the weight w^? We may use the solution to the second problem
in Section 12.6 together with some elementary trigonometry and obtain
W^ =
COSQf.
A whole circle can be represented by piecing several such arcs together. For
example, we might choose to represent a circle by three equal arcs, resulting in
a configuration like that shown in Figure
12.11.
The angles a equal 60 degrees,
and so the weights of the inner Bezier points are 1/2, whereas the junction Bezier
points have weights of unity, since each arc is in standard form.
Our representation of the circle is C^, assuming uniform parameter intervals;
see (12.16). It is not C^, however! Still we have an exact representation of the
circle, not an approximation. Thus this particular representation of the circle is
an example of a G^ curve.
We should mention that the parametrization of our circle is not the arc length
parametrization as explained in Chapter 10. If uniform traversal of the circle is
necessary for some application, we have no choice but to resort to the classical
sine and cosine representation. It can be shown (Farouki and Sakkalis [226]) that
no rational curve other than the straight line is parametrized with respect to arc
3 The actual size of the control polygon does not matter, of
course:
it can be changed by a
scaling to any size we want, and scalings do not affect the weights!

12.8 Control Vectors 223
length: when evaluated at equal increments of its parameter t^ the curve v^ill not
be traced out at uniform speed.
12.8 Control Vectors
In principle, any arc of a conic may be v^ritten as a rational quadratic curve
segment (possibly v^ith negative w^eights). But w^hat happens for the case w^here
the tangents at bg and hi become parallel? Intuitively, this v^ould send b^ to
infinity. A little bit of analysis w^ill overcome this problem, as wt shall see from
the foUov^ing example.
Let a conic be given by bo =
[—1,
0]^,b2 =
[1,
0]^,
and b^ = [0,tancy]^ and a
v^eight Wi = c cos a (v^e assume standard form). The angle a is formed by bob^
and bob2 at bg. Note that for c = 1, w^e obtain a circular arc, as illustrated in
Figure 12.12.
The equation of our conic is given by
(1
- ty
c(t) =
0
+ cos a
•
2ct{l
—
t)
0
tan
Of
+
^"
(1 - t)^ + 2ct(l - t) cos a + fi
bo b2
Figure 12.12 Conic arcs: a 168-degree arc of a circle is shown. Note that a is close to 90 degrees.

224 Chapter 12 Conic Sections
What happens as a tends to 7r/2? For the Hmiting conic, we obtain the equation
(1 -1)^
c(t) =
-1
0
+ 2t{l -1)
+
t^
[J]
(1
-
0^
+
t^
(12.24)
The problem of a weight tending to zero and a control point tending to infinity
has thus been resolved. For c = 1, we obtain a semicircle; other values of c give
rise to different conies. For c =
—
1,
we obtain the "lower" half of the unit circle.
We have been able to overcome possible problems with parallel end tangents.
But there is a price to be paid: if we look at (12.24) closely, we see that it does
not constitute a barycentric combination any more! The factors of
bo
and b2 sum
to one identically, hence [0, c]^ must be interpreted as a vector. Thus (12.24)
contains both control points and control vectors."^ An important property of
Bezier curves is thus lost, namely, the convex hull property: it is defined only for
point sets, not for a potpourri of points and vectors.
The use of control vectors allows a very compact form of writing a semi-
circle. But two disadvantages argue against its use: first, the loss of the convex
hull property. Second: to write the control vector form in the context of "normal"
rational quadratics, one will have to resort to a special case treatment. We shall
see later (Section 13.6) how to avoid the use of the control vector form.
1
2.9 Implementation
The following routine solves the first problem in Section 12.6:
float conic_weight(b0,bl,b2,p)
/*
Input:b0,bl,b2: conic control polygon vertices
p:
point
on
conic
Output: weight of bl (assuming standard
form).
Note:
will crash
in
"forbidden" situations.
V
4 In projective geometry, vectors are sometimes called points at infinity. This has given rise
to the name
infinite control
points by Versprille
[601];
see also L. Piegl
[477].
We prefer
the term control
vector
since this allows us to distinguish between
[0,
c^ and [0, —c^.

12.10 Problems 225
12.10 Problems
1 Equation (12.22) does not always have a solution. Identify the "forbidden"
regions for the third point p on the conic.
2 In the same manner, investigate (12.23).
3 Prove that the four tangent theorem holds for parabolas.
* 4 Establish the connection betw^een (12.12) and the four tangent theorem.
*5 Our discussion of the implicit form (12.21) w^as somev^hat academic: in
a "real-life" situation, (12.21) will never be satisfied exactly. Discuss the
tolerance problem that arises here; that is, how closely does (12.21) have
to be satisfied for a point to be within a given tolerance to the conic?
PI Write a routine to iteratively subdivide a conic, putting each piece into
standard form. The middle weights will converge to unity. How do the
convergence rates depend on the type of the initial conic.^ (See also [403].)
P2 Write a routine to approximate a given Bezier curve by a sequence of elliptic
arcs within a given tolerance.
This Page Intentionally Left Blank

Rational Bezier
and B-Spline Curves
tvational B-spline curves^ have become the standard curve and surface descrip-
tion in the field of CAD and graphics. The use of rational curves in CAGD may
be traced to Coons
[124], [126],
and Forrest
[240].
By now, there are books on
NURBS:
Fiorot and Jeannin
[233],
Farin
[202],
Piegl and Tiller
[482].
15.1 Rational Bezier Curves
In Chapter 12, we obtained a conic section in E^ as the projection of a parabola
(a quadratic) in E^. Conic sections may be expressed as rational quadratic
(Bezier) curves, and their generalization to higher-degree rational curves is quite
straightforward: a rational Bezier curve of degree n in E^ is the projection of
an wth degree Bezier curve in E^ into the hyperplane iv =\. We may view this
4D hyperplane as a copy of E^; we assume that a point in E"* is given by its
coordinates [ x y z tf ] . Proceeding in exactly the same way as we did for
conies, we can show that an «th degree rational Bezier curve is given by
Mt) =
woB"{t) + --- + w„B"(t) '•
x(0,b,eE^
(13.1)
The Wj art again called weights; the
b^
form the control polygon. It is the projec-
tion of the 4D control polygon [ Wjhi
Wj
] of the nonrational 4D preimage of
x(t).
1 Often called NURBS for nonuniform
rational
B-spUnes.
227

228 Chapter 13 Rational Bezier and B-Spline Curves
If all weights equal one, we obtain the standard nonrational Bezier curve, since
the denominator is identically equal to one.^ If some
Wj
are negative, singularities
may occur; we will therefore deal only with nonnegative Wj, Rational Bezier
curves enjoy all the properties that their nonrational counterparts possess; for
example, they are affinely invariant. We can see this by rewriting (13.1) as
x(t) = 2_^bi-
i=0
Tto"'.^r«
We see that the basis functions
sum to one identically, thus asserting affine invariance. If all
Wi
are nonnegative,
we have the convex hull property. We also have symmetry, invariance under
affine parameter transformations, endpoint interpolation, and the variation di-
minishing property. Obviously, the conic sections from the preceding chapter are
included in the set of all rational Bezier curves, further justifying their increasing
popularity.
The
Wi
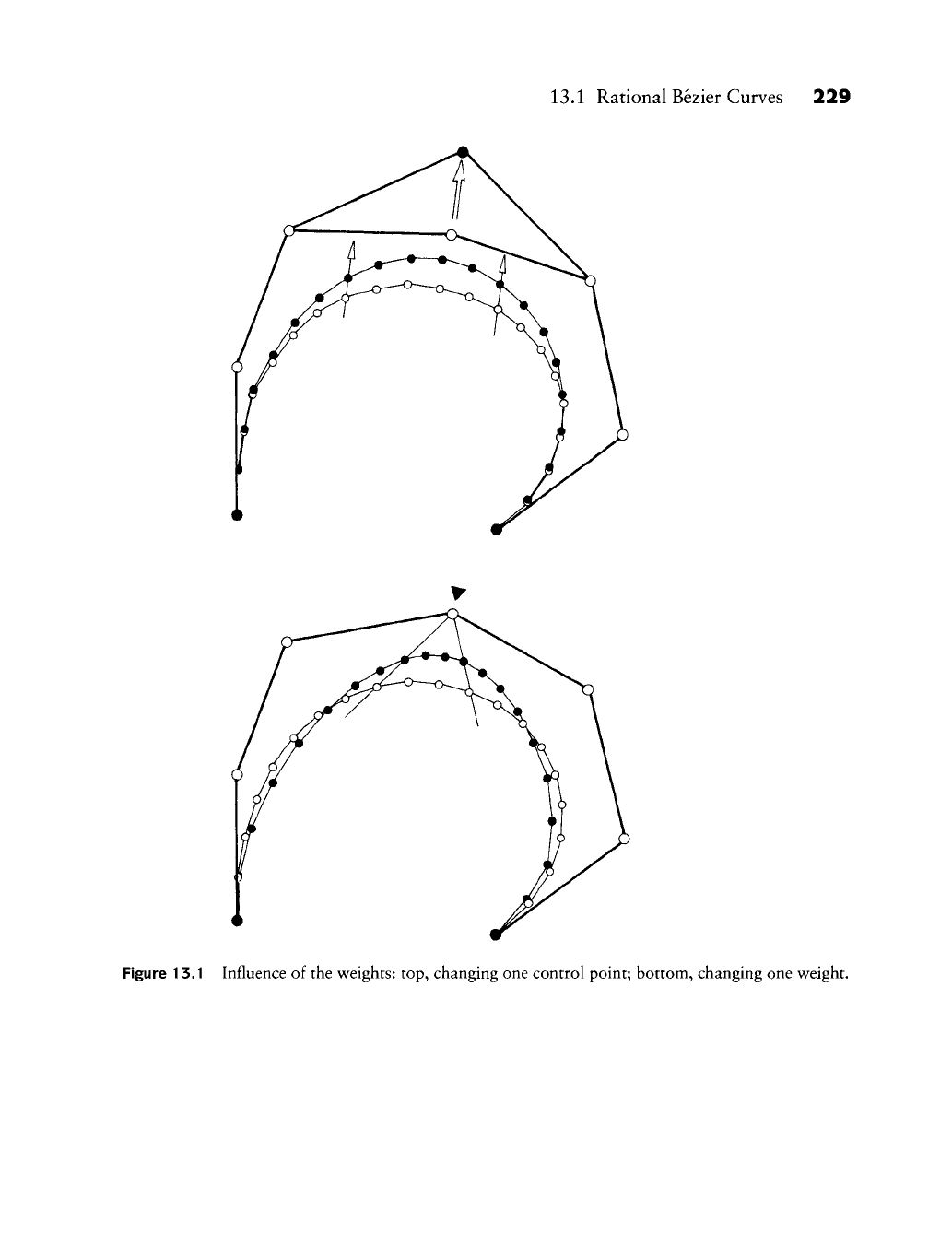
are typically used as shape parameters. If we increase one w//, the curve
is pulled toward the corresponding
b/,
as illustrated in Figure
13.1.
Note that the
effect of changing a weight is different from that of moving a control vertex. If we
let all weights tend to infinity at the same rate, we do not approach the control
polygon since a common (if large) factor in the weights does not matter—the
rational Bezier curve shape parameters behave differently from y- or y-spline
shape parameters.
Two properties differ from the nonrational case. First, we have projective
invariance; that is, if a rational Bezier curve is transformed by a projective
transformation, we could just as well apply that transformation to the control
polygon (using its weights to write it in homogeneous form) and would end up
with the same curve. Note that nonrational curves have this property only for
a subset of all projective maps, that is, the affine maps. The second difference
is the linear precision property. Rational curves may have all Bezier points b/
distributed on a straight line in a totally arbitrary fashion:
hi = (1 - a/)bo + a,b„; / = 0,...,
w
This is also true if
the
weights are not unity, but are equal to each other—a common factor
does not matter.
13.1 Rational Bezier Curves 229
Figure 13.1 Influence of the weights: top, changing one control point; bottom, changing one weight.

230 Chapter 13 Rational Bezier and B-Spline Curves
Figure 13.2 Weight
points:
changing one weight point influences the shape of
the
curve. Weight points
are marked by diamonds.
with arbitrary real numbers aj. We can still find weights
Wj
such that the resulting
curve traces out the straight line bob^ in
2i
linear fashion. They are given by
W^Q
= ^
and
i
!-«/-!
. 1
Wj = ^/-i; / =
1,...,
w.
n-\-l
—
i aj
For proofs, see [211] and
[234].
Rational Bezier curves may be modified in another way. Let us define weight
points qi by setting
q, = • . (13.2)
Wi + Wi^i
These points are defined via the weights; they may be used as shape parameters
for the curve. If we change the location of one of the q^, we may recompute a
new set of weights by setting
WQ
= 1 and using (13.2) as a recursion for the Wj,
Figure 13.2 illustrates.
15.2 The de Casteljau Algorithm
A rational Bezier curve may be evaluated by applying the de Casteljau algorithm
to both numerator and denominator and finally dividing through. A warning is
appropriate: though simple and usually effective, this method is not numerically
stable for weights that vary significantly in magnitude. If some of the
Wj
are large,
the 3D intermediate points [wjhjj (interpreted as points in a given coordinate
system) are no longer in the convex hull of the original control polygon {bj; this
may result in a loss of accuracy.-^
3 These points are obtained by applying the de Casteljau algorithm to the control points
Wjhj
of the numerator of
(13.1).
They have no true geometric interpretation because their
location is not invariant under translations of the original control polygon.

13.2 The de Casteljau Algorithm 231
An expensive yet more geometric technique is to project every intermediate
de Casteljau point [ Wjhj
Wj
] ; b/ e E^ into the hyperplane w = l. This yields
the rational de Casteljau algorithm (see Farin [193]):
mt)
=
a- 0-VK + i^^^v
(13.3)
^ WW ^
v^ith
w'^it) = (1- t)w'r\t) + tw'-_l{t). (13.4)
An explicit form for the intermediate points b[ is given by
h\{t) =
TU^t+i^it)
Note that for positive weights, the b^ are all in the convex hull of the original b/,
thus assuring numerical stability.
The rational de Casteljau algorithm allows a nice geometric interpretation.
While the standard de Casteljau algorithm makes use of ratios of three points,
this one makes use of the cross ratio of four points. Let us define points q^CO?
which are located on the straight lines joining b[ and b[^, subdividing them in
the ratios
ratio(b^,q^,b;:^l) = ^.
^ w
We shall call these points weight points^ because they indicate the relative mag-
nitude of the weights in a geometric way. Then all of the following cross ratios
are equal:
cr(b^,q^,b^+l,b^^l) = i^ for all r,/.
For r = 0, the weight points
q/
= q, =
Wi + Wi^i
are directly related to the weights Wf. given the weights, we can find the q^, and
given the q^, we can find the weights Wi,^ Thus the q^ may be used as shape
4 To be precise, we can only find them modulo an—immaterial—common factor.
