Fabien B. Analytical System Dynamics: Modeling and Simulation

Подождите немного. Документ загружается.

68 2 Kinematics

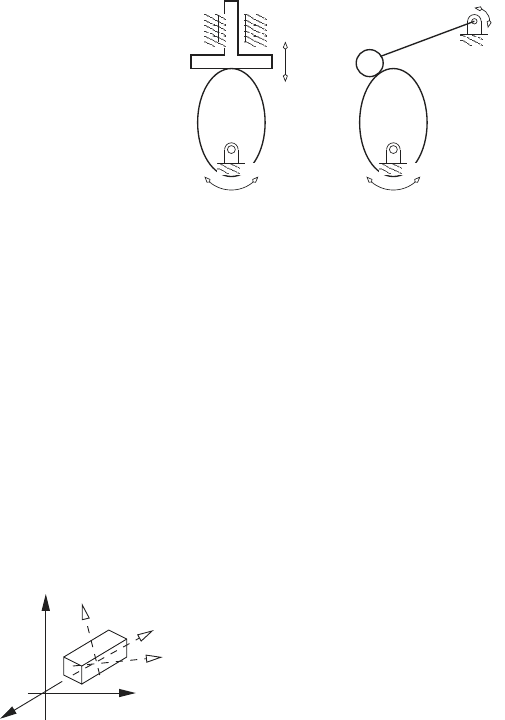
• Cam joint

Typical examples of cam pairs are shown below. At the point of con-

tact links 2 and 3 can roll and slide relative to each other.

Cam

Follower

(a) (b)

2.2.1 Mobility analysis

Fundamental to the dynamic analysis of mechanical devices is the determi-

nation of the mobility of the system, i.e., can the device move? This question

is answered by ﬁnding the number of degrees of freedom for the system. The

degrees of freedom are the minimum number of coordinates required to de-

termine the position and orientation of the mechanism.

To develop a methodology for determining the number of degrees of free-

dom in a particular mechanism consider the mobility of the following systems.

• Spatial rigid-body motion

Consider a rigid-body that is free to move in space.

In this case we require six coordinates to determine

the position and orientation of the body. Speciﬁ-

cally, if the rectangular coordinate system, x

-y

, is attached to the body then, three coordinates

are required to determine the location of the ori-

gin of the x

-y

-z

system with respect to the x-y-z

system.

In addition three coordinates are required to establish the direction cosine

matrix relating x

-y

-z

to x-y-z. Thus, this system has 6 degrees of free-

dom.

• Planar rigid-body motion

2.2 Mechanisms 69

Consider a rigid-body that is constrained to move

in the x-y plane. In this case we require three coor-

dinates to determine the position and orientation

of the body. If the rectangular coordinate system,

-y

, is attached to the body then, two coordi-

nates are required to determine the location of the

origin of the x

-y

system with respect to the x-y

system.

The orientation of the x

-y

system relative to the x-y system is determine

by a single angle. Thus, a rigid body that is constrained to move in a plane

has 3 degrees of freedom.

• A revolute joint

Consider the motion of a link about a revolute

joint. In this system one link is ﬁxed (i.e., the

ground) and the other is free to rotate. If the an-

gle θ is known then we can determine the position

of ever point on the link. Thus, this system has 1

degree of freedom. When compared to spatial mo-

tion of a rigid-body it can be seen that the revolute

joint removes 5 degrees of freedom.

When compared to plane motion of a rigid-body it can be seen that the

revolute joint removes 2 degrees of freedom.

• A prismatic joint

Consider the motion of a link about a prismatic

joint. In this system one link is ﬁxed (i.e., the

ground) and the other is free to slide (translate).

Hence, the displacement x is all that is required to

determine the position and orientation of the link.

Thus, this system has 1 degree of freedom.

When compared to spatial motion of a rigid-body it can be seen that the

prismatic joint removes 5 degrees of freedom. When compared to plane

motion of a rigid-body it can be seen that the prismatic joint removes 2

degrees of freedom.

• Pure rolling

70 2 Kinematics

For this system the disk is constrained to roll with-

out slipping. In which case the translation of the

center of the disk is directly related to the angle

of rotation. Thus, in pure rolling the system has 1

degree of freedom.

If the disk can simultaneously roll and slip then, two coordinates are re-

quired to determine the position and orientation of the system.

Using these examples we can develop an expression to determine the mo-

bility of a mechanical system. Let l be the number of links in the system, and

j be the number of joints. If all the links in the system are unconstrained the

system will have F = λl degrees of freedom, where λ = 6 for spatial motion,

and λ = 3 for planar motion. However, the i-th joint in the mechanism re-

moves λ−f

degrees of freedom, where f

is the number of degrees of freedom

allowed at the joint. Moreover, since the ground link is ﬁxed, λ degrees must

also be removed.

Thus, a general formula for determining the degrees of freedom in a mech-

anism is given by

F = λ(l −j − 1) +

i=1

, (2.20)

where F is the number of degrees of freedom, λ = 6 for spatial mechanisms,

λ = 3 for planar mechanisms, l is the number of links, j is the number of

joints, and f

is the number of degrees of freedom allowed by the i-th joint.

The formula (2.20) is known as Gruebler’s equation. When using Gruebler’s

equation note the following:

1. The ground is treated as a link.

2. All joints are assumed to connect only two links. If more than two links

are connected at a joint, then the joint is counted as n

− 1 joints, where

is the number of links connected to the joint.

Example 2.9.

This example applies equation 2.20 to the mechanisms shown in Fig. 2.6.

• R-R robot

This planar mechanism has l = 3 links and j = 2 joints. The revolute

joints (at A and B) each allow 1 degree of freedom. Thus, equation (2.20)

gives

F = λ(l − j − 1) +

i=1

2.2 Mechanisms 71

= 3(3 − 2 − 1) + 1 + 1

= 2.

Therefore, we require two coordinates to specify, uniquely, the position

and orientation of this mechanism. Note that robot mechanisms are often

classiﬁed by the types of joints in the system. Hence the term ‘R-R’ is used

to indicate that the robot has two revolute joints in sequence.

• Slider crank

The planar slider crank mechanism has l = 4 links, and j = 4 joints.

The joints at A, B and C are revolute joints, and each allow 1 degree of

freedom. The prismatic joint at D allows 1 degree of freedom. The number

of degrees of freedom for the mechanism is

F = λ(l − j − 1) +

i=1

= 3(4 − 4 − 1) + 1 + 1 + 1 + 1

= 1.

• Fourbar mechanism

The planar fourbar mechanism has l = 4 links and j = 4 joints. All of the

joints are revolute joints. Thus the degrees of freedom for the mechanism

is given by

F = λ(l − j − 1) +

i=1

= 3(4 − 4 − 1) + 1 + 1 + 1 + 1

= 1.

• Geared fourbar mechanism

The planar mechanism has l = 4 links and j = 4 joints. The joints

at A, B and C are revolute joints, and each allow 1 degree of freedom.

The pure rolling joint at D allows 1 degree of freedom. Thus the degrees

of freedom for the mechanism is given by

F = λ(l − j − 1) +

i=1

= 3(4 − 4 − 1) + 1 + 1 + 1 + 1

= 1.

72 2 Kinematics

For certain mechanisms equation (2.20) may indicate that there are fewer

degrees of freedom than actually present. Typically, such mechanism require

a speciﬁc geometry in order to have mobility. This is illustrated in the next

example.

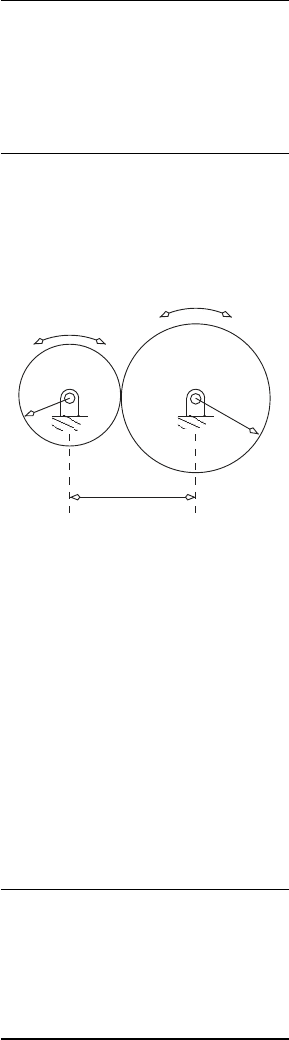
Example 2.10.

The ﬁgure below shows two circular rollers in contact. This system has l = 3

links and j = 3 joints (two revolute joints and a pure rolling joint).

The application of equation (2.20) gives the degrees of freedom as

F = λ(l − j − 1) +

i=1

= 3(3 − 3 − 1) + 1 + 1 + 1

= 0.

However, if the rollers are both precisely circular, and r

+ r

= d then,

the system will have 1 degree of freedom. If the rollers are not precisely

manufactured then the system will jam. (Gears/rollers that are noncircular

can also be made to undergo pure rolling by satisfying the criteria that the

sum of the radii of both gears must be equal to the distance between the

centers of rotation.)

Equation (2.20) can sometimes reveal passive degrees of freedom that ex-

ist in certain mechanisms. These are coordinates whose variation does not

produce any change in the other system coordinates. This is illustrated in

the next example.

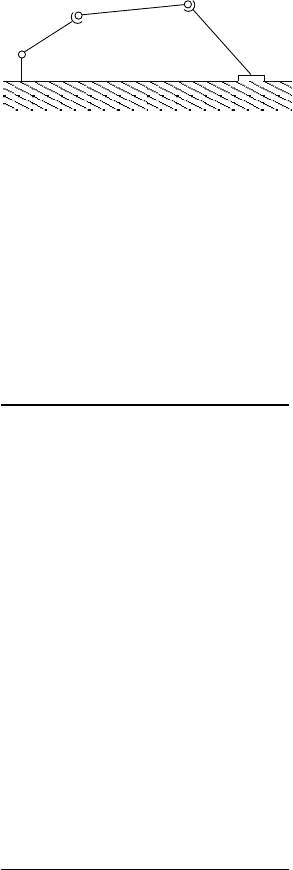
2.2 Mechanisms 73

Example 2.11.

The device shown here is a spatial fourbar mechanism. The systems has

revolute joints at A and D, and spherical joints at B and C.

The application of equation (2.20) gives,

F = λ(l − j − 1) +

i=1

= 6(4 − 4 − 1) + 1 + 3 + 3 + 1

= 2.

One of these degrees of freedom is the rotation of the link 2 about the line

BC. Such a rotation will not cause any other motion thus, this degree of

freedom is considered to be passive.

2.2.2 Kinematic analysis

With the results from the previous sections we are now well equipped to

perform the kinematic analysis of mechanisms. Here we take a direct approach

that is summarized by the following steps;

1. Perform a structural analysis of the mechanism to determine its mobility,

i.e., the number of degrees of freedom, F .

2. Attach a coordinate system to each moving link (rigid body) in the mech-

anism. As a result there will be λ(l − 1) coordinates associated with the

system (λ = 6 for spatial mechanisms, and λ = 3 for planar mechanisms).

3. Use the kinematic condition at the joints to determine λ(l − 1) − F con-

straint equations. These constraint equations ensure the proper behavior

of the joint.

This procedure is illustrated via several examples.

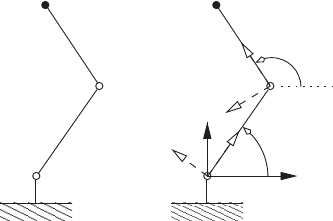
Example 2.12.

74 2 Kinematics

A schematic of an R-R robot is shown below. Here we are interested in

ﬁnding the equations required to determine the position and velocity of the

point C. The distance from A to B is l

, and the distance from B to C is l

The rectangular coordinate system x-y with origin Q represents the ﬁxed

system. The rectangular coordinate system x

-y

is attached to the link 1,

with origin at A, and the rectangular coordinate system x

-y

is attached to

the link 2, with origin at B, as shown in the ﬁgure. The orientation of the

-y

system relative to the x-y system is determined by the angle θ

. The

angle θ

measures the angular displacement if the x

-y

system relative to

the ﬁxed frame.

As noted above the system has 2 degrees of freedom however, the two

moving frames require 6 coordinates i.e.,





: the position of the origin of the x

-y

frame,

: the orientation of the x

-y

frame,





: the position of the origin of the x

-y

frame,

: the orientation of the x

-y

frame.

Let θ

and θ

be the independent coordinates for the system, i.e., the

degrees of freedom. Then 4 constraint equations are required to determine

, y

, x

, and y

in terms of θ

and θ

. These equations are determined

using the properties of the revolute joints. Speciﬁcally, the point A and Q are

coincident at all times hence, we have the constraints

= x

= 0,

= y

= 0.

Also, the coordinate of the point B is

which gives

the two constraints

= x

− l

cos θ

= 0,

= y

− l

sin θ

= 0.

2.2 Mechanisms 75

Here,

is the direction cosine matrix relating the x

-y

coordinate system

to the x-y coordinate system, and

is the coordinate of B relative to A

in the x

-y

coordinate system.

The coordinate of the point C is given by











cos θ

− sin θ

sin θ

cos θ







cos θ

− sin θ

sin θ

cos θ







cos θ

+ l

cos θ

sin θ

+ l

sin θ



where

is the direction cosine matrix relating the x

-y

coordinate system

to the x-y coordinate system, and

is the coordinate of C relative to B

in the x

-y

coordinate system.

Finally, the velocity of the point C can be computed via a direct diﬀeren-

tiation of the position of C, i.e.,

(

) =

˙r

˜ω(

) +

˜ω(

)



˙x

˙y





cos θ

−sin θ

sin θ

cos θ



0 −







cos θ

−sin θ

sin θ

cos θ



0−







−

sin θ

−

sin θ

cos θ



The plots below show the position and velocity of the point C for the

R-R robot with the proportions, l

= 2, and l

= 1. The angles θ

= 2πt,

and θ

= 20πt, where t is the time. The plots show the trajectory of the

system in the interval 0 ≤ t ≤ 1. The ﬁrst plot shows the path traced by the

point C, the second and third plots show, respectively, the x-axis and y-axis

components of the velocity of C.

76 2 Kinematics

−5

−1

Position of C

0 0.5 1

Velocity of x

time

0 0.5 1

Velocity of y

time

−100

−50

100

−100

−50

100

Example 2.13.

This example performs a kinematic analysis of a spatial R-R robot. A sketch

of the mechanism is shown in the diagram labeled (a). The motion generated

by this mechanism is spatial because the revolute joint at A allows rotation

about the vertical axis, while the revolute joint at B allows rotation about

an axis in the horizontal plane.

(a) (b)

(c)

2.2 Mechanisms 77

The diagrams (b) and (c) show the coordinate system assignment for the

mechanism. The rectangular coordinate system x-y-z with origin Q repre-

sents the ﬁxed frame. The rectangular coordinate system x

-y

-z

is attached

to the link AB with origin at A. The rectangular coordinate system x

-y

-z

is attached to the link BC with origin at B. The link AB has length l

, and

the link BC has length l

The diagram (b) shows the mechanism in the x-y plane, and the diagram

allows angular displacement θ

of the y

-axis only while, the revolute joint

at B allows angular displacement θ

of the z

-axis only. Note that the angle

is measured from the x

-axis.

A mobility analysis shows that the mechanism has 2 degrees of freedom.

However, the two moving frames require 12 variables to specify their position

and orientation. Of these 12 variables we will select θ

and θ

as the two

independent variables. The kinematic properties of the joints must be used

to determine 10 constraints that will account for the excess variables. As will

be seen many of these constraints are trivial.

First note that at all times the point Q, (the origin of the ﬁxed frame),

is coincident with A, the origin of the x

-y

-z

frame. This gives the three

constraints

= x

= 0,

= y

= 0,

= z

= 0.

Here, the orientation of the x

-y

-z

frame relative to the ﬁxed frame will

be described using the X

-Y

-Z

Euler angles. Due to the revolute joint

constraint it can be seen that the following two constraints must be satisﬁed;

= α

= 0,

= γ

= 0.

The coordinate of the point B (the origin of the moving frame x

-y

-z

)

is given by





















cos θ

0 sin θ

0 1 0

−sin θ

0 cos θ













Here,

is the direction cosine matrix relating x

-y

-z

to the ﬁxed frame,

and

is the coordinate of B relative to A in the x

-y

-z

coordinate

system. These equations lead to the three constraints

= x

− l

cos θ

= 0,