Fabien B. Analytical System Dynamics: Modeling and Simulation
Подождите немного. Документ загружается.


58 2 Kinematics
=
ρ(ω
C
+ ω
Z
sin α) − l
1
ω
Z
− l
2
ω
Z
cos α
0
0
.
2.1.5 Euler angles
It is perhaps apparent from the previous sections that the nine elements of
the direction cosine matrix,
0
A
1
, are not all independent. In fact since the
columns of
0
A
1
are orthogonal we have the following three constraints;
a
T
1
a
2
= a
11
a
12
+ a
21
a
22
+ a
31
a
32
= 0,
a
T
1
a
3
= a
11
a
13
+ a
21
a
23
+ a
31
a
33
= 0,
a
T
2
a
3
= a
12
a
13
+ a
22
a
23
+ a
32
a
33
= 0.
Here, a
i
is the i-th column of
0
A
1
.
Moreover, since the columns of
0
A
1
represents unit vectors we have the
three additional constraints;
|a
1
| =
q
a
2
11
+ a
2
21
+ a
2
31
= 1,
|a
2
| =
q
a
2
12
+ a
2
22
+ a
2
32
= 1,
|a
3
| =
q
a
2
13
+ a
2
23
+ a
2
33
= 1.
These six constraints imply that only three variables are required to deter-
mine the orientation of one rectangular system with respect to another.
In this text we use three Euler-angles as the independent variables that
determine the direction cosine matrix. The description of the Euler angles
utilizes rectangular coordinate systems called an intermediate frames. These
intermediate frames are used to show how the x-y-z system can be brought
into alignment with the x
1
-y
1
-z
1
system. The Euler angles are three successive
angular displacements that causes an intermediate frame, that is initially
aligned with frame 0, to be aligned with frame 1. These rotations take place,
in a particular order, about the x-axis, y-axis, or z-axis of the intermediate
frame.
To denote the axis of rotation, the angle of rotation, and the sequence of
rotations we use the following notation.
• X
α
indicates that the x-axis of the intermediate frame rotates an amount
α. Similarly, Y
β
indicates that the y-axis of the intermediate frame rotates
an amount β, and Z
γ
indicates that the z-axis of the intermediate frame
rotates an amount γ.
2.1 Mechanical Systems 59
• Z
α
-X
β
-Z
γ
denotes the following sequence of rotations are performed on
the intermediate frame; (i) rotate the z-axis an amount α, then (ii) rotate
the x-axis an amount β, finally (iii) rotate the z-axis an amount γ.
There are twelve possible sequences of such rotations that can be used to
obtain the direction cosine matrix. For example, X
α
-Y
β
-Z
γ
, X
α
-Y
β
-X
γ
, X
α
-
Z
β
-Y
γ
, etc. Here, we will consider the two sequences that are used frequently.
Namely, the sequence X
α
-Y
β
-Z
γ
and the sequence Z
α
-X
β
-Z
γ
.
X
α
-Y
β
-Z
γ
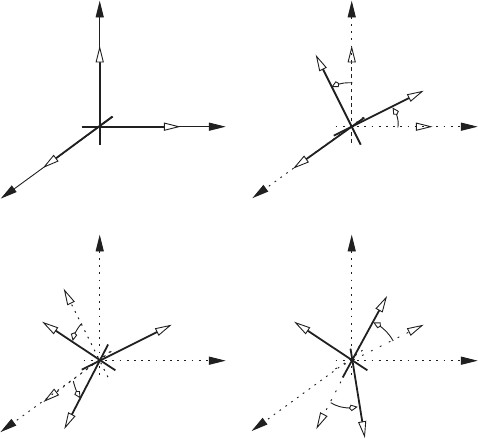
Euler angles
In Fig. 2.5a the origin of the fixed frame is labeled Q. Let the unit vectors
ˆ
i,
ˆ
j, and
ˆ
k, be directed along the x-axis, y-axis, and z-axis respectively. To
establish the Euler angles let x
a
-y
a
-z
a
be a rectangular coordinate system
with origin Q
a
that coincides with Q. Moreover, the x
a
, y
a
, and z
a
axes are
aligned with x, y, and z directions respectively (see Fig. 2.5a). The interme-
diate frame x
a
-y
a
-z
a
can only rotate about the point Q.
c
x
y
1
z
1
Q
1
y
z
z
x
x
a
z
y
x
α
α
b
x
a
z
z
y
γ
x
γ
)d()c(
(b)(a)
Q
y
a
Q
a
a
a
y
a
b
b
y
x
z
x
z
y
β
β
c
b
c
b
b
c
c
c
1
Fig. 2.5 Finite rotations
Now consider the consequence of three successive finite rotations of x
a
-
y
a
-z
a
. First, rotate the axis x
a
an angle α in the counterclockwise direction
to obtain the new orientation x
b
-y
b
-z
b
of the moving frame (see Fig. 2.5b).
60 2 Kinematics
Thus, after rotation by the angle α, the x
a
axis becomes the x
b
axis, the y
a
axis becomes the y
b
axis, and the z
a
axis becomes the z
b
axis.
A point
b
r = [x
b
, y
b
, z
b
]
T
in the x
b
-y
b
-z
b
frame has coordinate
0
r =
[x, y, z]
T
in the x-y-z frame where
0
r =
0
A
b
b
r,
0
A
b
=
1 0 0
0 c
α
−s
α
0 s
α
c
α
,
c
α
= cos α, and s
α
= sin α. The matrix
0
A
b
is the direction cosine matrix
that relates the x
b
-y
b
-z
b
frame to the x-y-z frame.
Next, rotate the axis y
b
an angle β in the counterclockwise direction to
obtain the new orientation x
c
-y
c
-z
c
of the moving frame (see Fig. 2.5c). Thus,
after rotation by the angle β, the x
b
axis becomes the x
c
axis, the y
b
axis
becomes the y
c
axis, and the z
b
axis becomes the z
c
axis.
A point
c
r = [x
c
, y
c
, z
c
]
T
in the x
c
-y
c
-z
c
frame has coordinate r
b
=
[x
b
, y
b
, z
b
]
T
in the x
b
-y
b
-z
b
frame where
b
r =
b
A
c
c
r,
b
A
c
=
c
β
0 s
β
0 1 0
−s
β
0 c
β
,
c
β
= cos β, and s
β
= sin β. The matrix
b
A
c
is the direction cosine matrix
that relates the x
c
-y
c
-z
c
frame to the x
b
-y
b
-z
b
frame.
Finally, rotate the axis z
c
an angle γ in the counterclockwise direction
to obtain the new orientation x
1
-y
1
-z
1
of the moving frame (see Fig. 2.5d).
Thus, after rotation by the angle γ, the x
c
axis becomes the x
1
axis, the y
c
axis becomes the y
1
axis, and the z
c
axis becomes the z
1
axis.
A point
1
r = [x
1
, y
1
, z
1
]
T
in the x
1
-y
1
-z
1
frame has coordinate
c
r =
[x
c
, y
c
, z
c
]
T
in the x
c
-y
c
-z
c
frame where
c
r =
c
A
1
1
r,
c
A
1
=
c
γ
−s
γ
0
s
γ
c
γ
0
0 0 1
,
c
γ
= cos γ, and s
γ
= sin γ. The matrix
c
A
1
is the direction cosine matrix
that relates the x
1
-y
1
-z
1
frame to the x
c
-y
c
-z
c
frame.
Thus, after three successive rotations, (α about x
a
, β about y
b
and, γ
about z
c
), it can be seen that the point
1
r = [x
1
, y
1
, z
1
]
T
in the x
1
-y
1
-z
1
frame has coordinate
0
r = [x, y, z]
T
in the x-y-z frame where
0
r =
0
A
b
b
r =
0
A
b
b
A
c
c
r =
0
A
b
b
A
c
c
A
1
1
r =
0
A
1
1
r. (2.15)
The coordinate transformation matrix
0
A
1
is

2.1 Mechanical Systems 61
0
A
1
=
1 0 0
0 c
α
−s
α
0 s
α
c
α
c
β
0 s
β
0 1 0
−s
β
0 c
β
c
γ
−s
γ
0
s
γ
c
γ
0
0 0 1
=
c
β
c
γ
−c
β
s
γ
s
β
s
α
s
β
c
γ
+ c
α
s
γ
−s
α
s
β
s
γ
+ c
α
c
γ
−s
α
c
β
−c
α
s
β
c
γ
+ s
α
s
γ
c
α
s
β
s
γ
+ s
α
c
γ
c
α
c
β
. (2.16)
The elements of
0
A
1
are the direction cosines of the x
1
, y
1
, and z
1
, axes with
respect to the x, y, and z axes, in terms of the X
α
-Y
β
-Z
γ
Euler angles.
Given a direction cosine matrix
0
A
1
the corresponding Euler angles can
be determined using
α = tan
−1
−a
23
a
33
, β = sin
−1
a
13
, γ = tan
−1
−a
12
a
11
,
where a
ij
are the ij-th elements of
0
A
1
.
Example 2.7.
Compute the X
α
-Y
β
-Z
γ
Euler angles associated with the direction cosine
matrix
0
A
1
computed in Example 2.3.
Solution:
The direction cosine matrix is
0
A
1
=
0.35354 −0.61237 0.70710
0.92678 0.12682 −0.35355
0.12683 0.78034 0.61238
.
Therefore,
α = tan
−1
−a
23
a
33
= tan
−1
0.35355
0.61238
= 0.5236 radians,
β = sin
−1
a
13
= sin
−1
0.70710 = 0.7854 radians,
γ = tan
−1
−a
12
a
11
= tan
−1
0.61237
0.35354
= 1.0472 radians.
Unlike finite translations of the moving frame, the finite rotations of the
moving frame can not be treated as vector quantities. In particular, the order
in which the finite rotations occur has significance. To see this consider the
same three rotations, described above, but in reverse order. First, a rotation
γ about the z
a
axis to produce the x
b
-y
b
-z
b
orientation. Then, a rotation β
62 2 Kinematics
about the y
b
axis to produce the x
c
-y
c
-z
c
orientation. Finally, a rotation α
about the x
c
axis to produce the x
1
-y
1
-z
1
orientation. If
1
r = [x
1
, y
1
, z
1
]
T
is a point in the x
1
-y
1
-z
1
frame then its coordinate in the x-y-z frame is
0
r =
0
A
b
b
A
c
c
A
1
1
r =
0
A
1
1
r,
where
0
A
1
=
c
β
c
γ
s
α
s
β
c
γ
− c
α
s
γ
c
α
s
β
c
γ
+ s
α
s
γ
c
β
s
γ
s
α
s
β
s
γ
+ c
α
c
γ
c
α
s
β
s
γ
− s
α
c
γ
−s
β
s
α
c
β
c
α
c
β
. (2.17)
Here,
0
A
1
is the direction cosine matrix obtained from the Z
γ
-Y
β
-X
α
Euler
angle sequence. It is clear that, in general, the transformation
0
A
1
in equation
(2.16) is not equal the transformation in equation (2.17). Hence, successive
finite rotations can not be represented as simple vector summations.
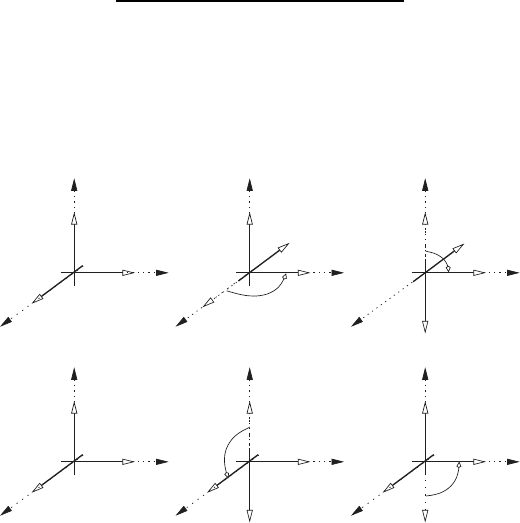
Example 2.8.
This figure shows the effect of reversing the order in which finite rotations
take place.
0
O
O
’
y
z
z
x
y
0
0
0
x
O
O
’
y
z
z
x
y
0
0
0
x
z
y
x
x
x
y
z
2
2
2
z
1
z
y
0
y
2
z
x
z
1
x
0
+90 y+90 z
+90 y +90 z
x
2
0
1
1
1
1
1
1
1
1
2
o
o
o
o
In the first sequence the frame x
0
-y
0
-z
0
rotates 90
◦
counterclockwise about
the z
0
axis. This is followed by a rotation 90
◦
counterclockwise about the y
1
axis.
In the second sequence the frame x
0
-y
0
-z
0
rotates 90
◦
counterclockwise
about the y
0
axis. This is followed by a rotation 90
◦
counterclockwise about
the z
1
axis.

2.1 Mechanical Systems 63
As can be seen the final orientation of the frame is different if the order of
the rotations is changed.
Angular velocity
A kinematic analysis requires the angular velocity of the moving frame. If
the orientation of the moving frame is described using Euler angles then the
angular velocities should also be expressed in terms of the Euler angles. Our
objective here is to determine the angular velocities of the x
1
-axis, y
1
-axis,
and z
1
-axis in the case where the orientation of the moving frame is described
using the X
α
-Y
β
-Z
γ
Euler angles.
By construction (see Fig. 2.5) the angular velocity of the moving frame
can be written as
1
¯ω = ˙α
ˆ
i
a
+
˙
β
ˆ
j
b
+ ˙γ
ˆ
k
c
, (a)
where
ˆ
i
a
is the unit vector along the x
a
-axis,
ˆ
j
b
is the unit vector along the
y
b
-axis, and
ˆ
k
c
is the unit vector along the z
c
-axis,
Now, the direction cosine matrix relating the x
1
-y
1
-z
1
system to the x
a
-
y
a
-z
a
system is
0
A
1
. (Note that x
a
-y
a
-z
a
is aligned with x-y-z.) Thus,
ˆ
i
a
=
ˆ
i = c
β
c
γ
ˆ
i
1
− c
β
s
γ
ˆ
j
1
+ s
β
ˆ
k
1
. (b)
The direction cosine matrix relating the x
1
-y
1
-z
1
system to the x
b
-y
b
-z
b
sys-
tem is
b
A
1
=
b
A
c
c
A
1
=
c
β
c
γ
−c
β
s
γ
s
β
s
γ
c
γ
0
−s
β
c
γ
s
β
s
γ
c
β
.
Therefore,
ˆ
j
b
= s
γ
ˆ
i
1
+ c
γ
ˆ
j
1
. (c)
The direction cosine matrix relating the x
1
-y
1
-z
1
system to the x
c
-y
c
-z
c
sys-
tem is
c
A
1
, which shows that
ˆ
k
c
=
ˆ
k
1
. (d)
Using (b), (c) and (d) in (a) gives
1
¯ω = ˙α(c
β
c
γ
ˆ
i
1
− c
β
s
γ
ˆ
j
1
+ s
β
ˆ
k
1
)
+
˙
β(s
γ
ˆ
i
1
+ c
γ
ˆ
j
1
) + ˙γ
ˆ
k
1
,
= ( ˙αc
β
c
γ
+
˙
βs
γ
)
ˆ
i
1
+ (− ˙αc
β
s
γ
+
˙
βc
γ
)
ˆ
j
1
+ ( ˙αs
β
+ ˙γ)
ˆ
k
1
=
1
ω
1
ˆ
i
1
+
1
ω
2
ˆ
j
1
+
1
ω
3
ˆ
k
1
.
Here,
1
ω
1
is the angular velocity of the x
1
-axis,
1
ω
2
is the angular velocity
of the y
1
-axis, and
1
ω
3
is the angular velocity of the z
1
-axis. This result can

64 2 Kinematics
be put in matrix form to get
1
ω
1
1
ω
2
1
ω
3
=
c
β
c
γ
s
γ
0
−c
β
s
γ
c
γ
0
s
β
0 1
˙α
˙
β
˙γ
. (2.18)
Given the angular velocities
1
ω
1
,
1
ω
2
, and
1
ω
3
, equation (2.18) can be
inverted to find the rate of change of the Euler angles. Specifically,
˙α
˙
β
˙γ
=
1
c
β
c
γ
−s
γ
0
c
β
s
γ
c
β
c
γ
0
−s
β
c
γ
s
β
s
γ
c
β
1
ω
1
1
ω
2
1
ω
3
. (2.19)
Note that the coefficient matrix in equation (2.18) is singular when β = ±π/2.
Thus, at orientations of the moving frame where β = ±π/2 we will be unable
to compute the angular velocities.
All Euler angle sequence of rotations have singular points in the config-
uration space. To avoid computational difficulties we will select a sequence
of Euler angles that are not singular near the nominal configuration of the
system.
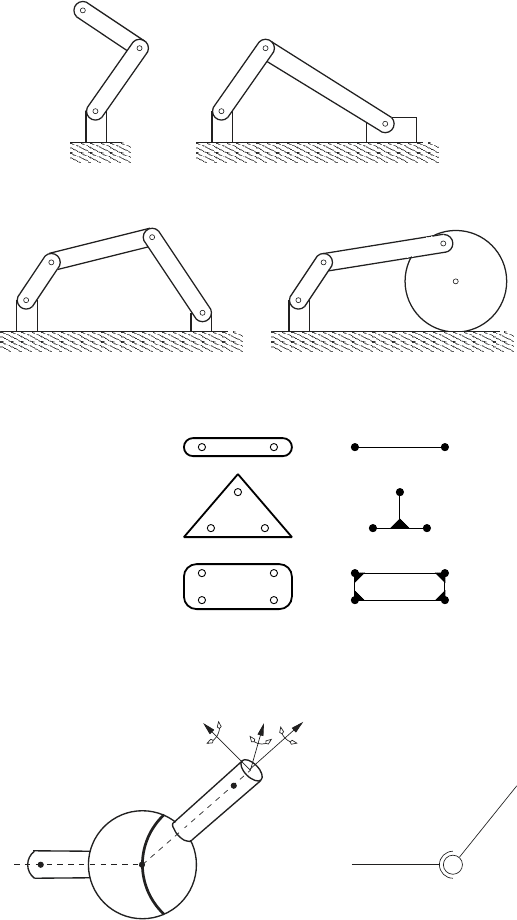
2.2 Mechanisms
Mechanisms are mechanical systems that consists of rigid bodies called links
that are connected at points called joints. Figure 2.6 presents schematics
of some well known mechanisms. The links of a mechanism are classified
according to the number of joints that are on the link. As shown in Fig. 2.7
binary links have two joints, ternary links have three joints, quaternary links
have four joints, etc.
If each link in the mechanism is connected to at least two other links then
the mechanism forms a closed kinematic chain. Otherwise, the mechanism has
an open kinematic chain. In Fig. 2.6 the R-R robot has an open-kinematic
chain, all the other mechanisms are closed kinematic chains.
The joints in the mechanism are also called kinematic pairs. These kine-
matic pairs permit relative motion between the links in the mechanism. More-
over, the joints are classified according to the type of motion allowed between
the links. The kinematic pairs considered in this text are as follows.
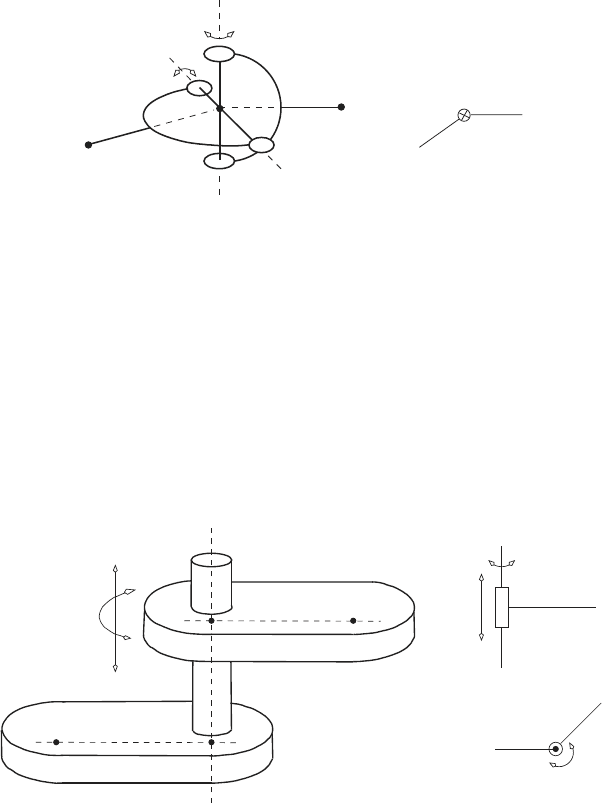
• Spherical joint
A schematic of a spherical joint is shown below. This kinematic pair
allows link 1 and link 2 to rotate relative to each other about three axes.
2.2 Mechanisms 65
D
R−R Robot Slider−crank mechanism
Geared fourbar mechanismFourbar mechanism
A
1
B
C 2
4
A
2
3
B
C
D
1
1
A
B
4
2
C
D
3
1
2
3
4
A
B
C
Fig. 2.6 Mechanisms
Quaternary
Binary
Ternary
Fig. 2.7 Types of links
1
1
Link 1
Link 2
P
1
Q
2
P
2
γ α
β
S
2
Q
At each instant the point P
1
on link 1 and the point Q
2
on link 2 are
coincident. The symbol S is used to denote a spherical joint.
• Universal joint
A schematic of a universal joint is shown below. This kinematic pair al-
66 2 Kinematics
lows link 1 and link 2 to rotate relative to each other about two orthogonal
axes.
U
1
Q
2
P
1
γ
α
Z
Z
X
X
P
2
Link 1
Link 2
1
2
Q
At each instant the point P
1
on link 1 and the point Q
2
on link 2 are co-
incident. In addition the links can rotate relative to each other about the
orthogonal lines XX and ZZ. The symbol U is used to denote a universal
joint.
• Cylindrical joint
The cylindrical joint allows rotation and translation of the links rela-
tive to each other. A sketch of a cylindrical joint is shown below. Let L
1
be the line that passes through the point P
1
on link 1 and the point Q
2
on
link 2. Then at a cylindrical joint, link 2 can simultaneously rotate about
the line L
1
and translate along the line L
1
.
z
2
C
1
2
1
C
Link 1
Link 2
γ
Q
P
1
Q
2
P
2
L
1
L
1
1
The symbol C is used to denote a cylindrical joint.
• Revolute joint
The revolute joint allows rotation of the links relative to each other.
A sketch of a revolute joint is shown below. Let L
1
be the line that passes
through the point P
1
on link 1 and the point Q
2
on link 2. Then at a
revolute joint, link 2 can only rotate about the line L
1
.
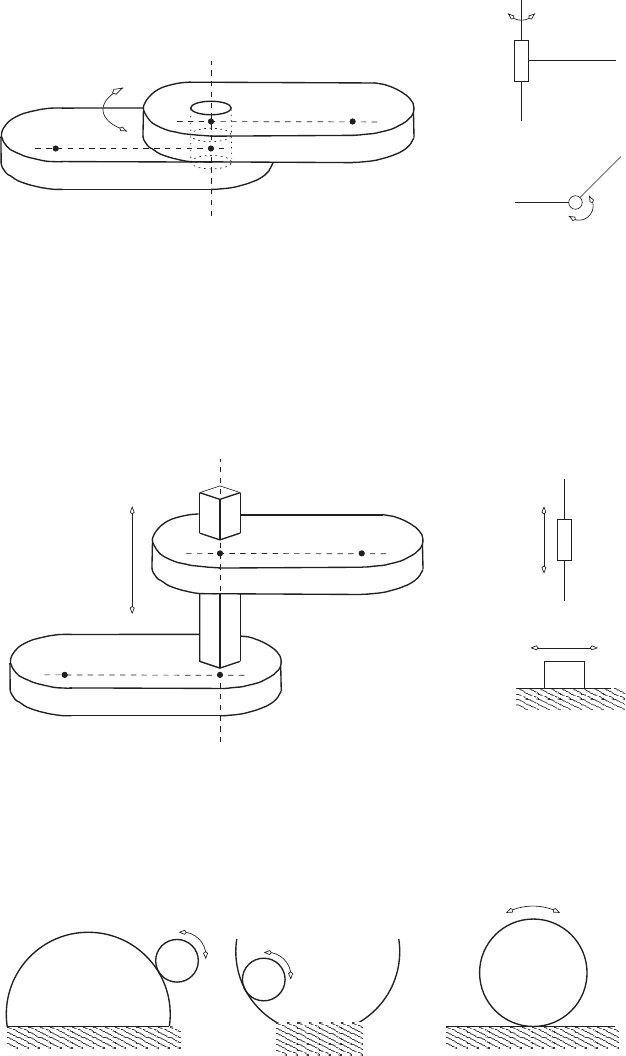
2.2 Mechanisms 67
1
Link 1
Link 2
γ
2
R
1
2
R
Q
P
1
P
2
Q
2
L
1
L
1
1
The symbol R is used to denote a revolute joint.
• Prismatic joint
The prismatic joint allows translation (sliding) of the links relative to
each other. A sketch of a prismatic joint is shown below. Let L
1
be the
line that passes through the point P
1
on link 1 and the point Q
2
on link
2. Then, at a prismatic joint, link 2 can only translate along the line L
1
.
Link 2
1
P
2
1
2
P
Link 1
z
1
1
P
1
Q
2
P
2
L
1
L
Q
The symbol P is used to denote a prismatic joint.
• Rolling joint
The rolling pair shown below allows link 2 to roll on link 1 without slipping.
2
1
11
2
2
