Fabien B. Analytical System Dynamics: Modeling and Simulation
Подождите немного. Документ загружается.

88 2 Kinematics
system. This equation yields the constraints,
φ
7
= l
1
cos θ
1
+ l
2
cos θ
2
− x
C
= 0,
φ
8
= l
A
+ l
1
sin θ
1
+ l
2
sin θ
2
= 0.
Given a value for the crank angle, θ
2
, the 8 equations φ
1
, φ
2
, ···, φ
8
can be
used to solve for the coordinates x
A
, y
A
, x
B
, y
B
, θ
2
, x
C
, y
C
, and θ
3
. Clearly
many of the equations are trivial however, φ
7
and φ
8
are coupled nonlinear
equations that must be solved to determine θ
2
and x
C
.
To find the velocity of the point C we differentiate equation (a) with
respect to time to get
˙x
C
˙y
C
=
−l
1
˙
θ
1
sin θ
1
− l
2
˙
θ
2
sin θ
2
l
1
˙
θ
1
cos θ
1
+ l
2
˙
θ
2
cos θ
2
.
However, we know from φ
5
that ˙y
C
= 0. These last two equations yield the
linear system
−l
2
sin θ
2
1
l
2
cos θ
2
0
˙
θ
2
˙x
C
=
l
1
˙
θ
1
sin θ
1
−l
1
˙
θ
1
cos θ
1
,
which must be solved to determine
˙
θ
2
and ˙x
C
.
Finally, it can be seen that the position and velocity of the point E are
given by
x
E
y
E
=
l
1
cos θ
1
+ l
E
cos θ
2
l
A
+ l
1
sin θ
1
+ l
E
sin θ
2
,
and
˙x
E
˙y
E
=
−l
1
˙
θ
1
sin θ
1
− l
E
˙
θ
2
sin θ
2
l
1
˙
θ
1
cos θ
1
+ l
E
˙
θ
2
cos θ
2
,
respectively.
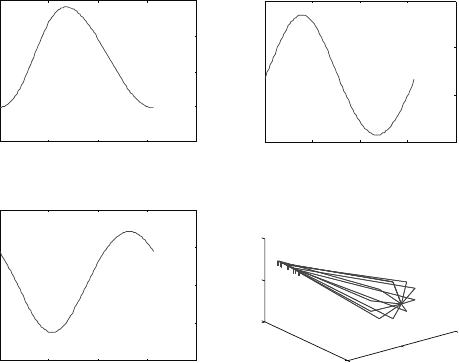
The trajectory of the slider crank mechanism, described above, is shown in
the figures below. These results are obtained using a crank angular velocity
˙
θ
1
= 2π. The first plot shows the coupler angle θ
2
versus the crank angle θ
1
.
The second plot shows the slider position x
C
versus θ
1
. The third plot shows
the path traced by the point E. The fourth plot shows the configuration of the
mechanism in ten different positions. This plot also shows the path traced by
the point E. The remaining plots shows the velocities of the system variables
as a function of θ
1
.

2.2 Mechanisms 89
0 2 4 6 8
5
5.5
6
θ
1
θ
2
0 2 4 6 8
0
2
4
6
θ
1
x
c
0 1 2 3 4
0
1
2
3
4
x
E
y
E
−2 0 2 4 6
−2
0
2
4
6
x
E
y
E
0 2 4 6 8
−4
−2
0
2
4
θ
1
(d/dt) θ
2
0 2 4 6 8
−10
0
10
20
θ
1
(d/dt) x
c
0 2 4 6 8
−15
−10
−5
0
5
10
θ
1
(d/dt)x
E
0 2 4 6 8
−5
0
5
Example 2.18.
The diagrams below show the front and top views of a spatial slider crank
mechanism. The device has moving binary links at AB, CB and DC. The
joint at A is revolute and the direction of rotation is along an axis parallel

90 2 Kinematics
to the line Y Y . In addition the line AB makes a fixed angle, ψ, with respect
to the line ZZ (in the front view). The joint at B is a spherical joint, the
joint at C is a universal joint, and the joint at D is a prismatic joint. The
translation in the prismatic joint takes place parallel to the line Y Y . The link
AB has length l
1
, and the link CB has length l
2
.
Z
A
R
S
U
B
A
Top view
ψ
B
Front view
Y
Y
Y Y
P
b
C
D
C
c
d
Z
A mobility analysis of the mechanism shows that there are l = 4 links,
j = 4 joints and
F = λ(l −j − 1) +
j
X
i=1
f
i
= 6(4 − 4 − 1) + (1 + 3 + 2 + 1) = 1
degree of freedom.
The rectangular coordinate system x-y-z, shown in the figure below, rep-
resents the fixed frame for the system. The rectangular coordinate system
x
1
-y
1
-z
1
is attached to the link AB with origin at A, and y-axis parallel to
the line Y Y . The rectangular coordinate system x
2
-y
2
-z
2
is attached to the
link DC with origin at D, and y-axis parallel to the line Y Y (in the direction
of translation for the prismatic joint). The rectangular coordinate system x
3
-
y
3
-z
3
is attached to the link CB with origin at C, and y-axis along the line
CB.

2.2 Mechanisms 91
D
3
y
1
1
z
2
z
x
3
y
2
3
z
B
y
A
z
C
y
The three moving frames require a total of 18 variables to describe the
position and orientation of the system however, there is only 1 degree of
freedom. Hence, 17 constraint equations are required to determine the ex-
cess variables in terms of the independent coordinate. Here, we will take the
angular displacement of the link AB as the independent variable.
To determine the needed constraints we will establish the position and
orientation of each coordinate frame ensuring that the kinematic conditions
allowed at each joint is satisfied. Consider the x
1
-y
1
-z
1
coordinate system.
The position of A gives the three constraints
φ
1
= x
A
= 0, φ
2
= y
A
− l
A
= 0, φ
3
= z
A
= 0.
The orientation of x
1
-y
1
-z
1
is defined by the X
α
1
-Y
β
1
-Z
γ
1
Euler angles. Thus,
to satisfy the kinematic conditions, for the revolute joint at A, we must have
the two constraints
φ
4
= α
1
= 0, φ
5
= γ
1
= 0.
Consider the x
2
-y
2
-z
2
coordinate system. To satisfy the kinematic condi-
tions for the prismatic joint at D we must have the two constraints
φ
6
= x
D
+ d = 0, φ
7
= z
D
− b = 0.
The orientation of the x
2
-y
2
-z
2
coordinate system is defined using the X
α
2
-
Y
β
2
-Z
γ
2
Euler angles. Since the x
2
-y
2
-z
2
coordinate system remains parallel
to the x-y-z coordinate system we have the three constraints
φ
8
= α
2
= 0, φ
9
= β
2
= 0, φ
10
= γ
2
= 0.
Consider the x
3
-y
3
-z
3
coordinate system. The coordinates of the origin of
the system (point C) satisfy the three constraints
φ
11
= x
C
− x
D
= 0, φ
12
= y
C
− y
D
= 0, φ
13
= z
C
− z
D
− c = 0.
The orientation of the x
3
-y
3
-z
3
coordinate system is defined using the X
α
3
-
Y
β
3
-Z
γ
3
Euler angles. Since the joint at C is a universal joint it allows two
rotations about orthogonal axes. Here, we assume that the two rotations are
α
3
and γ
3
. Thus, the third angle must satisfy the constraint
92 2 Kinematics
φ
14
= β
3
= 0.
The remaining three constraints are determined by noting that the mech-
anism forms a closed kinematic chain, i.e.,
0
A
1
1
r
AB
=
0
r
QD
+
0
A
2
2
r
DC
+
0
A
2
2
A
3
3
r
CB
, (a)
where
0
A
1
=
c
β
1
0 s
β
1
0 1 0
−s
β
1
0 c
β
1
,
1
r
AB
=
0
l
1
s
ψ
l
1
c
ψ
,
0
r
QD
=
−d
y
D
b
,
0
A
2
=
1 0 0
0 1 0
0 0 1
,
2
r
DC
=
0
0
c
,
2
A
3
=
c
γ
3
− s
γ
3
0
c
α
3
s
γ
3
c
α
3
c
γ
3
− s
α
3
s
α
3
s
γ
3
s
α
3
c
γ
3
c
α
3
,
3
r
CB
=
0
l
2
0
.
Here,
0
A
1
is the direction cosine matrix relating the x
1
-y
1
-z
1
coordinate sys-
tem to the fixed frame,
1
r
AB
is the coordinate of B relative to A in the
x
1
-y
1
-z
1
coordinate system,
0
r
QD
is the coordinate of D relative to Q in the
fixed frame,
0
A
2
is the direction cosine matrix relating the x
2
-y
2
-z
2
coordi-
nate system to the fixed frame,
2
r
DC
is the coordinate of C relative to D in
the x
2
-y
2
-z
2
coordinate system,
2
A
3
is the direction cosine matrix relating
the x
3
-y
3
-z
3
coordinate system to the x
2
-y
2
-z
2
coordinate system, and
3
r
CB
is the coordinate of B relative to C in the x
3
-y
3
-z
3
coordinate system.
Equation (a) yields the three constraints
φ
15
= l
1
c
ψ
s
β
1
+ d + l
2
s
γ
3
= 0,
φ
16
= l
1
s
ψ
− y
D
− l
2
c
α
3
c
γ
3
= 0,
φ
17
= l
1
c
ψ
c
β
1
− b − c − l
2
s
α
3
c
γ
3
= 0.
Given a crank angle β
1
the 17 constraints φ
1
, φ
2
, ···, φ
17
can be used to
determine the system coordinates. Note that all but the last three constraints
are trivial. The constraints φ
15
, φ
16
, and φ
17
form a system of nonlinear
equations that determine y
D
, α
3
and γ
3
.
To determine the velocity of slider, ˙y
D
, we differentiate the last three
constraints with respect to time to get
l
2
c
γ
3
0 0
l
2
c
α
3
s
γ
3
l
2
s
α
3
c
γ
3
−1
l
2
s
α
3
s
γ
3
−l
2
c
α
3
c
γ
3
0
˙γ
3
˙α
3
˙y
D
=
−
˙
β
1
l
1
c
ψ
c
β
1
0
˙
β
1
l
1
c
ψ
s
β
1
. (b)
2.2 Mechanisms 93
Thus, given β
1
, α
3
, γ
3
, and
˙
β
1
, the linear equation (b) can be used to de-
termine the slider velocity ˙y
D
, and the rate of change of angular position
˙α
3
and ˙γ
3
. Note that ˙α
3
and ˙γ
3
are not the angular velocities of the x
3
-axis
and z
3
-axis, respectively. In fact using equation (2.18) it can be seen that the
angular velocities of the x
3
-y
3
-z
3
coordinate system satisfies
3
ω
1
3
ω
2
3
ω
3
=
c
β
3
c
γ
3
s
γ
3
0
−c
β
3
s
γ
3
c
γ
3
0
s
β
3
0 1
˙α
3
˙
β
3
˙γ
3
.
Here,
3
ω
1
is the angular velocity of the x
3
-axis,
3
ω
2
is the angular velocity
of the y
3
-axis, and
3
ω
3
is the angular velocity of the z
3
-axis. Due to the
kinematic constraints at joint C (a universal joint), the rotation β
3
= 0, and
˙
β
3
= 0. Thus, the angular velocities of the x
3
-y
3
-z
3
coordinate system are
3
ω
1
=c
γ
3
˙α
3
,
3
ω
2
= −s
γ
3
˙α
3
, and
3
ω
3
= ˙γ
3
.
The behavior of the spatial slider crank mechanism analyzed above is
illustrated in the figures below. In these plots the constraint equations are
solved for a mechanism with the following proportions; ψ=π/6.0, l
1
=1.0,
l
2
=4.0, d=2.0, b=1.0, and c=0.25. The angular velocity of the crank, AB, is
˙
β
1
=2π radians/second. The nonlinear equations φ
15
, φ
16
, and φ
17
are solved
using Newton’s method.
The first plot shows the Euler angle α
3
as a function of the crank angle β
1
.
The second plot shows the Euler angle γ
3
as a function of the crank angle.
The third plot shows the the slider position as a function of the crank angle.
The fourth plot shows the configuration in 10 different positions.
0 2 4 6 8
6.2
6.4
6.6
6.8
7
β
1
α
3
0 2 4 6 8
3.4
3.6
3.8
4
β
1
γ
3
0 2 4 6 8
2.5
3
3.5
4
4.5
β
1
y
D
−2
0
2
0
5
−2
0
2
x
y
z

94 2 Kinematics
The plots below show the angular velocities ˙α
3
, ˙γ
3
, and the slider velocity
˙y
D
as a function of the crank angle.
0 2 4 6 8
−2
0
2
4
β
1
(d/dt)α
3
0 2 4 6 8
−2
−1
0
1
2
β
1
(d/dt)γ
3
0 2 4 6 8
−10
−5
0
5
β
1
(d/dt)y
D
The plots below show the angular velocities
3
ω
1
,
3
ω
2
, and
3
ω
3
as a function
of the crank angle.
0 2 4 6 8
−2
−1
0
1
2
β
1
ω
1
0 2 4 6 8
−1
0
1
2
β
1
ω
2
0 2 4 6 8
−2
−1
0
1
2
β
1
ω
3

2.3 Network Systems 95
2.3 Network Systems
The models for electrical, fluid and thermal systems can be represented as
networks. The structure (topology) of these networks define the relationship
between the fundamental variables associated with the model. Here, we will
use some terminology and results from graph theory to describe the kinematic
constraints that exists in network systems.
R
v
+
R
2
C L
1
Fig. 2.9 A network system
The electrical circuit shown in Fig. 2.9 will be used to illustrate the pro-
cedure used to determine the kinematic behavior of network systems. The
basic steps of the method are as follows.
1. Node assignment:
The first step in the modeling technique is to assign a node to the points
of interconnection between the circuit components, as shown below.
(d)
v
+
R
2
C L
1
R
(a) (b) (c)
Node assignment
Thus, a node should be assigned to the terminals of each element in the
network. In this case we have nodes a, b, c and d.
2. Flow assignment:
A flow variable and a positive reference direction is assigned to each ele-
ment of the system. For flow sources the direction of positive flow is as-
signed a priori. In the case of an effort source the positive direction of flow
is taken from the negative terminal to the positive terminal of the source.
For all other system elements (ideal resistors, capacitors and inductors)
the reference direction of positive flow can be assigned arbitrarily.
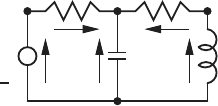
96 2 Kinematics
5
v
+
R
2
C L
1
R
(a) (b) (c)
(d)
i i
i i
i
1
2
3
4
Flow assignment
In the figure shown above we have assigned the flow i
1
through the voltage
source, i
2
through the resistor R
1
, i
3
through the capacitor, i
4
through the
resistor R
2
, and i
5
through the inductor. The actual flow directions, for
these passive elements, are determined by solving the dynamic equations
of motion.
Annotating a network model as described above can lead to a large number
of flow variables. However, due to the interconnections in the system not all
these flow variables are independent. In fact if we assume continuity of flow
at the nodes in the network then we can develop a set of equations that relate
the flow variables in the model. If continuity of flow is satisfied then the sum
of all the flows into a node must be zero. In the analysis of electrical circuits
this continuity principle is known as Kirchhoff’s current law.
As in mechanical systems it is important to know how many of the flow
variables are independent, i.e., how many degrees of freedom exists in the
network. To determine the number of independent flow variables in a network
we can borrow some results from graph theory.
Networks contain entities called nodes, branches, trees and chords. These
terms will be defined with the aid of the electrical circuit shown in Fig. 2.9.
This circuit contains the following system elements; an effort (voltage) source,
v(t), resistors R
1
and R
2
, a capacitor, C, and an inductor, L.
• Nodes:
The nodes in the network have already been defined above. These are the
points at the terminals of the system elements. Hence, a, b, c and d rep-
resent nodes in the network. Let N denote the number of nodes in the
network. (Therefore, N = 4 for the circuit in Fig. 2.9).
• Branches:
The system elements themselves are called branches in the network. Thus,
v(t), R
1
, R
2
, C and L are the branches of the network. Let B denote the
number of branches in the network. (Therefore, B = 5 for the circuit in
Fig. 2.9).
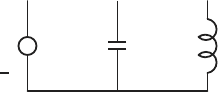
2.3 Network Systems 97
• Trees:
Given a network, if we remove the minimum number of branches such that
no closed loops remain, then the result is a tree. Thus, for the network
shown in Fig. 2.9 removing the branches R
1
and R
2
will give the tree
shown below.
L
v
+
C
A tree
Let T denote the number of branches in a tree, then it should be clear
that for any network with N nodes,
T = N − 1.
• Chords:
The chords are the branches that must be added to the tree so that the
network is complete. Let C denote the number of chords in the network.
Hence,
C = B − T = B − (N − 1) = B − N + 1.
The number of chords actually identify the number of independent closed-
loops in the network. Since each closed-loop only requires one flow variable,
C is equal to the number of independent flow variables in the network.
Applying this equation to the circuit in Fig. 2.9 shows that the system has
C = 5 − 4 + 1 = 2 degrees of freedom. However, there are 5 flow variables
assigned to the model. This indicates that there are three constraint equations
that relate the ‘excess’ variables to the independent variables. Let i
1
and i
4
be the independent flow variables then, assuming continuity of flow at nodes
a, b and c gives the three constraints
ψ
1
= i
1
− i
2
= 0,
ψ
2
= i
2
+ i
3
− i
4
= 0,
ψ
3
= i
5
− i
4
= 0.
The flow constraints ψ
1
, ψ
2
and ψ
3
can be used to eliminate the variables i
2
,
i
3
and i
5
from the model description.
