Fabien B. Analytical System Dynamics: Modeling and Simulation
Подождите немного. Документ загружается.


308 6 Dynamic System Analysis and Simulation
Therefore, the torque input (b) is such that the tracking error vanishes asymp-
totically.
The system simulation uses the following model parameters; l
1
= 0.65 m,
l
2
= 0.5 m, m
1
= 1.6 kg, m
2
= 1.2 kg, I
1
= 0.06 kg-m
2
, I
2
= 0.05 kg-m
2
.
The desired trajectory of the robot is,
q
1d
(t) =
π/4 if t < 2
0 if t ≥ 2
, q
2d
(t) = π/2.
The parameters for the controller are selected as ζ = 1.1 and ω = 5/
p
ζ
2
− 1.
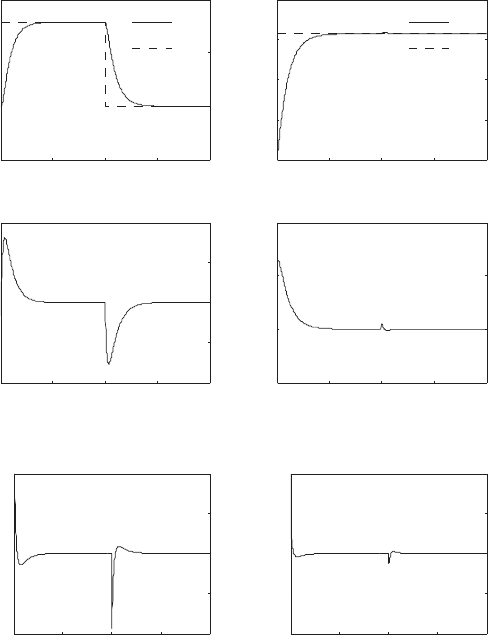
Figure 6.9 shows the result of the numerical simulation. The plot (i) shows
the response for the angle q
1
, and the desired angle q
1d
. The plot (ii) shows
the response for the angle q
2
, and the desired angle q
2d
. In both cases we can
see that the input torque allows the robot to follow the desired trajectory.
The angular velocities ˙q
1
and ˙q
2
are shown in plots (iii) and (iv), respectively.
Finally, plots (v) and (vi) show the torques τ
1
and τ
2
required to execute this
maneuver.
It should be noted that the actual implementation of the control (b) is
a nontrivial task. Since, it requires the measurements q
1
(t), q
2
(t), ˙q
1
(t) and
˙q
2
(t), as well as the model parameters. Other control techniques must be used
if any of this information is unknown, or is imprecise. For examples of such
control system designs see Craig (1986), and Slotine and Li (1991).
Example 6.18.
q
+
R
Lv
m
x
g
The schematic of an electromagnetic suspen-
sion is shown in the figure on the left. This de-
vice consists of a coil with inductance, L, and
resistance, R, that is actuated by the voltage
source v(t). The mass, m, is made of a highly
permeable magnetic material. For devices of
this type it can be shown that the coil induc-
tance satisfies an equation of the form
L(x) =
γ
0
γ
1
+ x
,
where γ
0
> 0 and γ
1
> 0 are parameters that depend on the material prop-
erties and the geometry of the system. In the system simulation given below
uses the following model parameters, m = 0.1 kg, R = 10 ohm, g = 9.8 m/s
2
,
γ
0
= 0.03 volt-m-s/amp, and γ
1
= 1 × 10
−5
m.
Kinematic analysis:
The network current ˙q and the displacement of the mass x are taken as
6.2 System Simulation 309
0 1 2 3 4
−0.5
0
0.5
1
t
q
1
(i)
q
1
q
1d
0 1 2 3 4
0
0.5
1
1.5
2
t
q
2
(ii)
q
2
q
2d
0 1 2 3 4
−4
−2
0
2
4
t
dq
1
/dt
(iii)
0 1 2 3 4
−5
0
5
10
t
dq
2
/dt
(iv)
0 1 2 3 4
−100
−50
0
50
100
t
τ
1
(v)
0 1 2 3 4
−100
−50
0
50
100
t
τ
2
(vi)
Fig. 6.9 Example 6.17
the generalized coordinates for the system. The variable x is also called the
air gap in electromagnetic suspensions.
Applied effort analysis:
The virtual work done by the applied voltage, v(t), and the weight, mg,
is
δW = v δq + mg δx.
Lagrange’s equations:
310 6 Dynamic System Analysis and Simulation
The kinetic coenergy for the system is T
∗
= L(x) ˙q
2
/2 + m ˙x
2
/2. The poten-
tial energy and dissipation function are V = 0 and D = R ˙q
2
/2, respectively.
Hence, Lagrange’s equations of motion for the system are
m¨x +
γ
0
˙q
2
2(γ
1
+ x)
2
= mg,
γ
0
γ
1
+ x
¨q −
γ
0
˙q ˙x
(γ
1
+ x)
2
+ R ˙q = v.
System simulation:
By defining the state variables q
1
= x, q
2
= ˙x and q
3
= ˙q, the equations
of motion for the system can be rewritten as the implicit differential equa-
tions
0 = ˙q
1
− q
2
,
0 = ˙q
2
+
γ
0
q
2
3
2m(γ
1
+ q
1
)
2
− g,
0 = ˙q
3
+
γ
1
+ q
1
γ
0
(Rq
3
− v) −
q
2
q
3
γ
1
+ q
1
.
Suppose the mass is suspended in an equilibrium position q
1
= q
10
=
1 × 10
−3
m and q
2
= 0 m/s. Then the corresponding current and input
voltage can be obtained from the equations of motion by setting ˙q
2
= ˙q
3
= 0
to get q
3
= q
30
=
p
2mg(γ
1
+ q
10
)
2
/γ
0
amp, and v = v
0
= Rq
30
volt. In this
equilibrium position the force developed by the coil is
f
coil
=
γ
0
q
2
30
2(γ
1
+ q
10
)
2
.
This coil force just balances the weight mg.
To examine the response of the system, if it is perturbed from the equilib-
rium position, consider the initial conditions q
1
(0) = q
10
+1×10
−4
m, q
2
= 0
m/s, and q
3
(0) = q
30
amp. In addition, the input voltage is set as v(t) = v
0
volt.
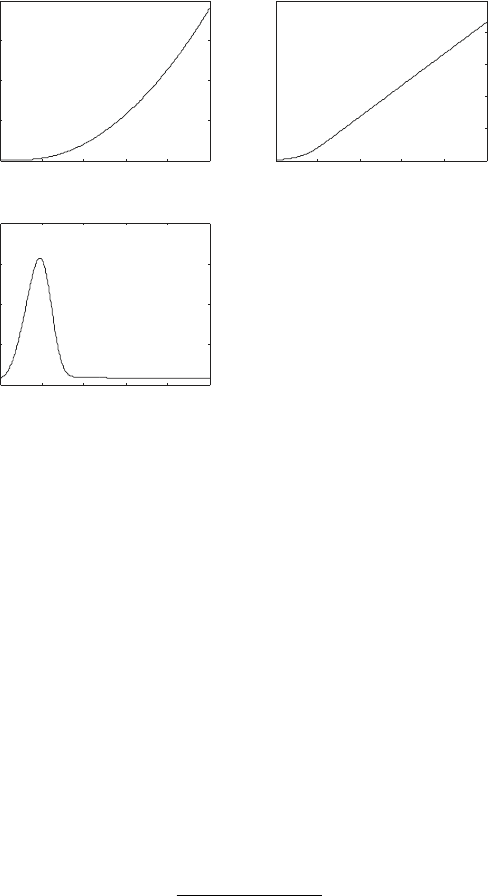
Figure 6.10 shows the response of the system to this initial condition. Here,
plot (i) shows the air gap, plot(ii) shows the velocity of the mass, and plot
(iii) shows the current in the coil. As can be seen the air gap, q
1
, deviates
quite far from the equilibrium position q
10
= 1 × 10
−3
m.
This type of motion illustrates an equilibrium position that is ‘unstable’.
In particular, an unstable equilibrium position is one for which a ‘small’
perturbation in the equilibrium position results in a trajectory that move
‘far’ away from the equilibrium position.
As described above the electromagnetic suspension is not very useful since,
any small disturbance will cause the system to move far away from its equi-
6.2 System Simulation 311
0 0.2 0.4 0.6 0.8 1
0
1
2
3
4
t
q
1
(i)
0 0.2 0.4 0.6 0.8 1
0
2
4
6
8
10
t
q
2
(ii)
0 0.2 0.4 0.6 0.8 1
0
0.05
0.1
0.15
0.2
t
q
3
(iii)
Fig. 6.10 Example 6.18 unstable response
librium. However, a number of techniques can be used to stabilize the equi-
librium of the device. These techniques involve adjusting the voltage input,
v, so that the air gap, q
1
, remains close to q
10
if the system is subject to small
disturbances. One such method can be described as follows.
Let z
1
= q
1
− q
10
= x − q
10
represent the change in the air gap, let
z
2
= q
2
= ˙x represent the velocity of the suspended mass, and let z
3
= ˙q
2
= ¨x
represent the acceleration of the suspended mass. Then, the equations of
motion can be written as
0 = ˙z
1
− z
2
,
0 = ˙z
2
− z
3
,
0 = ˙z
3
− u,
where
u =
q
3
(Rq
3
− v)
m(γ
1
+ z
1
+ q
10
)
.
Hence, by using the coordinate transformation from q
1
, q
2
, q
3
to z
1
, z
2
, z
3
,
and the input u we have made the dynamic equations of motion appear to
be linear.
Next, using the input u = −k
1
z
1
− k
2
z
2
− k
3
z
3
, where k
1
, k
2
and k
3
are
constants to be determined, the equations of motion become

312 6 Dynamic System Analysis and Simulation
d
3
z
1
dt
3
+ k
3
d
2
z
1
dt
2
+ k
2
dz
1
dt
+ k
1
z
1
= 0.
This third-order, linear ordinary differential equation determines the varia-
tion in the air gap z
1
(t). The general solution to this equation is
z
1
(t) = a
1
e
λ
1
t
+ a
2
e
λ
2
t
+ a
3
e
λ
3
t
,
where a
1
, a
2
and a
3
depend on the initial conditions z
1
(0), z
2
(0) and z
3
(0),
and λ
1
, λ
2
and λ
3
are the roots of the characteristic equation
λ
3
+ k
3
λ
2
+ k
2
λ + k
1
= 0.
In the system simulation below, the roots of the characteristic equation
are placed at λ
1
= −30, λ
2
= −20 + 10i and λ
3
= −20 − 10i, by selecting
k
1
= 15000, k
2
= 1700, and k
3
= 70. Using these coefficients it can be seen
that lim
t→∞
z
1
(t) = 0, for any nonzero initial condition. That is, the air gap
will eventually return to x = q
10
after some perturbation from the equilibrium
position.
To implement this control technique the voltage input to the system is
determined by
v = Rq
3
− m(γ
1
+ z
1
+ q
10
)u/q
3
= Rq
3
+ (m/q
3
)(γ
1
+ z
1
+ q
10
)(k
1
z
1
+ k
2
z
2
+ k
3
z
3
).
Thus, in an actual device this controller requires the knowledge of the states
z
1
, z
2
, z
3
and q
3
, as well as the model parameters m, R and γ
1
.
The simulation of the system with this nonlinear feedback controller is
shown in Fig. 6.11. These plots show the response of the system with initial
conditions q
1
(0) = q
10
+1×10
−4
m, q
2
= 0 m/s, and q
3
(0) = q
30
amp. As can
be seen the system is well behaved in this case, and the initial perturbation in
the air gap eventually vanishes. In this case the equilibrium position q
1
= q
10
,
q
2
= 0, q
3
= q
30
is made asymptotically stable using the voltage control input.
This result should be compared to the unstable system shown in Fig. 6.10.

6.2 System Simulation 313
0 0.5 1
0.5
1
1.5
2
x 10
−3
t
q
1
(i)
0 0.5 1
−0.01
−0.005
0
0.005
0.01
0.015
0.02
t
q
2
(ii)
0 0.5 1
0.008
0.01
0.012
0.014
0.016
t
q
3
(iii)
Fig. 6.11 Example 6.18 stable response
Example 6.19.
This example investigates the behavior of the
inverted pendulum system shown on the right.
The dynamic equations of motion for this
system are derived in Example 3.10. Here,
the system response is computed in following
cases; (i) The initial condition response about
the equilibrium position θ = π. (ii) The ini-
tial condition response about the equilibrium
position θ = π, with F = −c
1
˙x − c
2
˙
θ, where
c
1
and c
2
are positive constants. (iii) The ini-
tial condition response about the equilibrium
position θ = 0. (iv) The initial condition re-
sponse about the equilibrium position θ = 0,
and F determined using linear state feedback
control.
1
l
g
θ
F
2
m
x
m
x
y
O
Lagrange’s equations:
From Example 3.10 Lagrange’s equations of motion for the system are
(m
1
+ m
2
)¨x + m
2
l(
¨
θ cos θ −
˙
θ
2
sin θ) = F,
314 6 Dynamic System Analysis and Simulation
m
2
(l
2
¨
θ + l¨x cos θ) = m
2
gl sin θ.
These equations can be written as a system of first-order ordinary differential
equations using the state variables q
1
= x, q
2
= θ, q
3
= ˙x and q
4
=
˙
θ. With
this definition the equations of motion become
1 0 0 0
0 1 0 0
0 0 m
1
+ m
2
m
2
l cos q
2
0 0 m
2
l cos q
2
m
2
l
2
˙q
1
˙q
2
˙q
3
˙q
4
−
q
3
q
4
m
2
lq
2
4
sin q
2
+ F
m
2
gl sin q
2
= 0. (a)
System simulation:
The following model parameters are used in the simulations described be-
low; m
1
= 0.5 kg, m
2
= 0.1 kg, l = 0.25 m, and g = 9.8 m/s
2
.
Case 1: θ(0) = π and F = 0.
This simulation examines the motion of the system perturbed from the equi-
librium point,
q
∗
= [q
∗
1
, q
∗
2
, q
∗
3
, q
∗
4
]
T
= [0, π, 0, 0]
T
.
The point q
∗
is called an equilibrium point because the equations of motion
are satisfied identically with q(t) = q
∗
, ˙q(t) = 0, and F = 0. (Here, q(t) =
[q
1
(t), q
2
(t), q
3
(t), q
4
(t)]
T
.)
Now consider the response of the system with initial condition q(0) =
[0, π, 0, 0.1]. That is, the equilibrium position q
∗
is perturbed by an angular
velocity
˙
θ = q
4
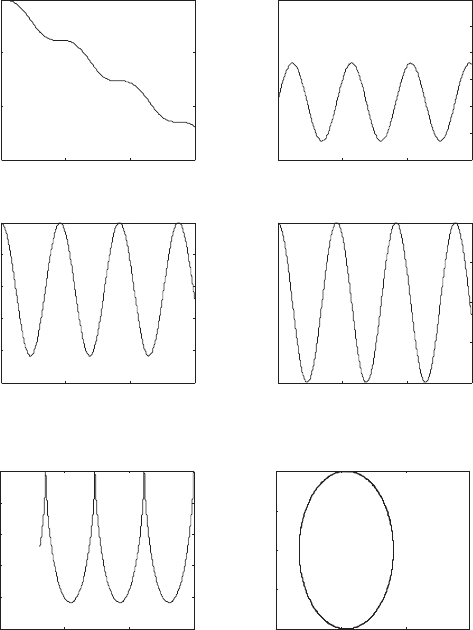
= 0.1. Figure 6.12 shows plots of the system trajectory. Here,
the plot (i) shows that q
1
moves to the left, while the plot (ii) shows that
q
2
= θ oscillates about the equilibrium q
2
= π. The velocities ˙q
1
= q
3
and
˙q
2
= q
4
are shown in plots (iii) and (iv), respectively.
Another view of the system response is illustrated in the state portraits
shown in plots (v) and (vi) of Fig. 6.12. Plot (v) shows q
1
versus q
3
, and
plot (ii) shows q
2
versus q
4
. Notice that q
2
-q
4
form a closed orbit around the
equilibrium position q
∗
.
Case 2: θ(0) = π and F = −c
1
˙x −c
2
˙
θ.
Here the force applied to the mass is F = −c
1
˙x−c
2
˙
θ, where c
1
and c
2
are pos-
itive constants. This is equivalent to adding a linear damper, with damping
coefficient c
1
to the mass m
1
, and a torsional damper with damping coeffi-
cient c
2
to the link l. As a result this force input can also be represented by
the dissipation function D = c
1
˙x
2
/2+c
2
˙
θ
2
/2 = c
1
q
2
3
/2+c
2
q
2
4
. The simulation
shown below uses c
1
= 2 N-s/m and c
2
= 0.5 N-m-s.
Using F = −c
1
q
3
−c
2
q
4
in the equations of motion it can be seen that q
∗
is
still an equilibrium point for the system. The response of this model starting
from the initial condition q(0) = [0, π, 0, 0.1]
T
is shown in Fig. 6.13. From
these plots it is observed that the system oscillates about the equilibrium
6.2 System Simulation 315
0 1 2 3
−0.015
−0.01
−0.005
0
t
q
1
(i)
0 1 2 3
3.12
3.13
3.14
3.15
3.16
3.17
3.18
t
q
2
(ii)
0 1 2 3
−0.01
−0.008
−0.006
−0.004
−0.002
0
t
q
3
(iii)
0 1 2 3
−0.1
−0.05
0
0.05
0.1
t
q
4
(iv)
−0.015 −0.01 −0.005 0
−0.01
−0.008
−0.006
−0.004
−0.002
0
q
1
q
3
(v)
3.12 3.14 3.16 3.18
−0.1
−0.05
0
0.05
0.1
q
2
q
4
(vi)
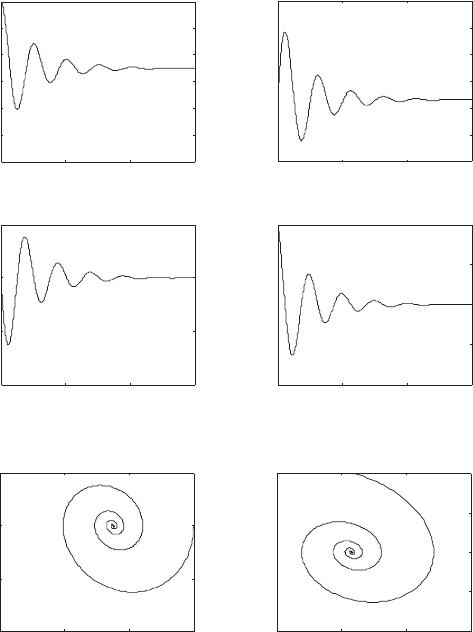
Fig. 6.12 Example 6.19: Case 1
with decreasing amplitude. In fact lim
t→∞
q(t) = q
∗
. That is, the perturbed
system eventually returns to the equilibrium q
∗
.
The state portraits of this response are shown in plots (v) and (vi), which
clearly shows that trajectory of the system is from the initial condition, q(0),
to the equilibrium q
∗
along a spiral path. Since the motion is such that
q(t) → q
∗
, the point q
∗
is called an asymptotically stable equilibrium. Thus,
when compared to Case 1, adding damping to the system has made the
equilibrium q
∗
asymptotically stable.
Case 3: θ(0) = 0 and F = 0.
The point ¯q = [0, 0, 0, 0]
T
is also an equilibrium of the system, since the
316 6 Dynamic System Analysis and Simulation
0 2 4 6
−3
−2.5
−2
−1.5
−1
−0.5
0
x 10
−3
t
q
1
(i)
0 2 4 6
3.13
3.135
3.14
3.145
3.15
3.155
3.16
t
q
2
(ii)
0 2 4 6
−10
−5
0
5
x 10
−3
t
q
3
(iii)
0 2 4 6
−0.1
−0.05
0
0.05
0.1
t
q
4
(iv)
−3 −2 −1 0
x 10
−3
−10
−5
0
5
x 10
−3
q
1
q
3
(v)
3.13 3.14 3.15 3.16
−0.1
−0.05
0
0.05
0.1
q
2
q
4
(vi)
Fig. 6.13 Example 6.19: Case 2
equations of motion are satisfied identically with q(t) = ¯q, ˙q(t) = 0 and
F = 0. Now, consider the initial condition q(0) = [0, 0, 0, 0.1]
T
which is a
perturbation from the equilibrium ¯q. The results of the system simulation, in
this case, are shown in Fig. 6.14. These plots show that the system trajectory
is such that the state q(t) moves ’far’ away from the equilibrium ¯q. As a
result, the point ¯q is called an unstable equilibrium in this case.
Case 4: θ(0) = 0 and F = −k
1
q
1
− k
2
q
2
− k
3
q
3
− k
4
q
4
.
This simulation shows that the unstable equilibrium ¯q can be made stable by
using a force input
F = −k
1
q
1
− k
2
q
2
− k
3
q
3
− k
4
q
4
,

6.2 System Simulation 317
0 1 2 3
−0.4
−0.3
−0.2
−0.1
0
t
q
1
(i)
0 1 2 3
0
5
10
15
t
q
2
(ii)
0 1 2 3
−0.4
−0.3
−0.2
−0.1
0
t
q
3
(iii)
0 1 2 3
0
5
10
15
t
q
4
(iv)
−0.4 −0.3 −0.2 −0.1 0
−0.4
−0.3
−0.2
−0.1
0
q
1
q
3
(v)
0 5 10 15
0
5
10
15
q
2
q
4
(vi)
Fig. 6.14 Example 6.19: Case 3
where k
1
, k
2
, k
3
and k
4
are constants. In control system terminology this is
called linear state feedback control.
To develop this result, first linearize the equations of motion about the
equilibrium point ¯q. Let q = ¯q + w, ˙q =
˙
¯q + ˙w, and F =
¯
F + u, where x, ˙x
and u are small variations in the state, state derivative and force input from
the equilibrium, respectively. Note that, for this system, at the equilibrium
point
˙
¯q = 0 and
¯
F = 0. Now, the equations of motion, (a), can be written
as Φ(q, ˙q, F ) = Φ(¯q + w,
˙
¯q + ˙w,
¯
F + u) = 0. Writing this equation as a Taylor
series centered at ¯q,
˙
¯q,
¯
F gives
Φ(¯q + w,
˙
¯q + ˙w,
¯
F + u) = Φ(¯q,
˙
¯q,
¯
F ) + Φ
˙q
˙w + Φ
q
w + Φ
F
u
