Fabien B. Analytical System Dynamics: Modeling and Simulation

Подождите немного. Документ загружается.

288 6 Dynamic System Analysis and Simulation

b=0.75;

Phi = zeros(2,1);

Phi(1,1) = yp(1)-y(2);

Phi(2,1) = m*yp(2) + b*y(2) + k*y(1);

return;

% end file: ex2_ide.m

% file: ex2_jacobian.m

function [J,M] = ex2_jacobian(y,yp,t)

m=0.3;

k=45.0;

b=0.75;

M = zeros(2,2);

J = zeros(2,2);

M(1,1) = 1;

M(2,2) = m;

J(1,2) = -1;

J(2,1) = k;

J(2,2) = b;

return;

% end file: ex2_jacobian.m

% file: ex2.m

clear all

m=0.3;

k=45.0;

b=0.75;

tspan = linspace(0,3,100)’;

y0 = [1.0e-2;0];

yp0 = [y0(2);-k*y0(1)/m];

[T,Y] = ride(’ex2_ide’,’ex2_jacobian’,tspan,y0,yp0);

% end file: ex2.m

The diﬀerential equation (b) can be written as

¨y

+ 2ζω ˙y

+ ω

= 0,

6.2 System Simulation 289

where ω

= k/m, ζ = (b/m)/(2ω), ω

= ω

(1 −ζ

). If ζ < 1 then, it can be

shown that the analytical solution to this diﬀerential equation is

(t) = y

(0)e

ζωt

cos ω

t +

1 − ζ

sin ω

˙y

(0)

−ζωt

sin ω

Recall that the condition ζ < 1 implies that the system response is ‘under-

damped’. If ζ = 1 then the system response is said to be ‘critically damped’.

If ζ > 1 the system response is said to be ‘overdamped’.

For the model parameters used here it can be seen that the system is

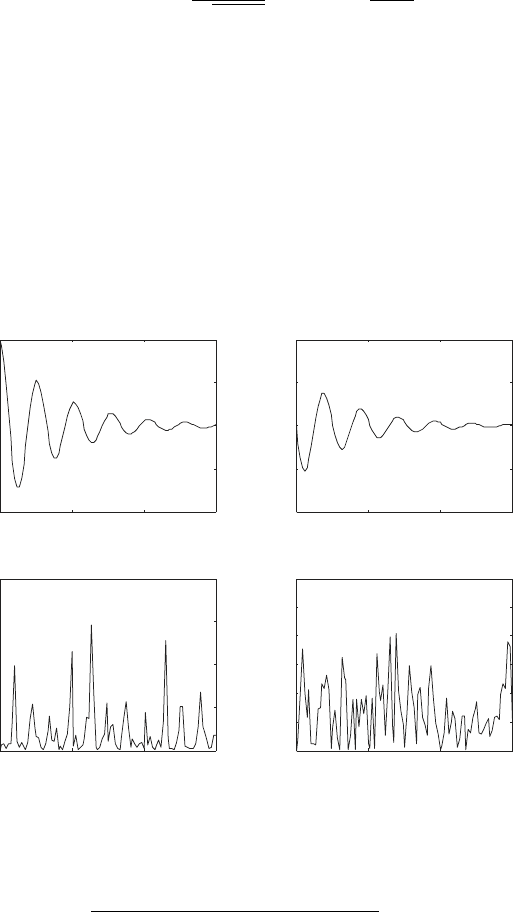
underdamped. The plots (i) and (ii) in Fig. 6.2 show the numerically com-

puted displacement and velocity of the system. The plots (iii) and (iv) in Fig.

6.2 show the absolute value of the error between the analytical solution and

the computed results. These ﬁgures indicate that the error in the numerical

solution is well below the speciﬁed error tolerance.

0 1 2 3

−0.01

−0.005

0.005

0.01

(i)

0 1 2 3

−0.2

−0.1

0.1

0.2

(ii)

0 1 2 3

x 10

−8

(iii)

error|

0 1 2 3

0.5

1.5

2.5

x 10

−7

(iv)

error|

Fig. 6.2 Example 6.12

290 6 Dynamic System Analysis and Simulation

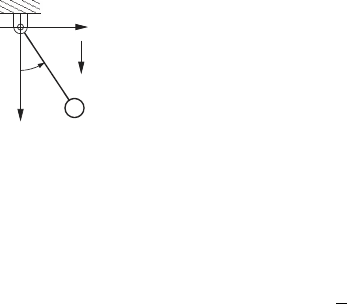
Example 6.13.

This example simulates the behavior of the simple pendu-

lum shown here using two diﬀerent models of the system.

In the ﬁrst model the angle θ is taken as the generalized

displacement. In the second model the variables q

and q

are used as the displacement coordinates for the system.

Using θ as the generalized displacement we can show that

Lagrange’s equation of motion is

θ + mgl sin θ = 0. (a)

If we deﬁne the state variables y

= θ and y

θ then, (a) can be rewritten

as the implicit diﬀerential equations

0 = ˙y

− y

0 = ˙y

sin y

(b)

The parameters for this model are m = 0.25 kg, l = 0.3 m, and g = 9.8 m/s

The initial conditions are θ = y

= π/2 and

θ = y

= 0.

The m-ﬁles required to simulate this version model are shown below.

% file: ex3a_ide.m

function Phi = ex3a_ide(y,yp,t)

m = 0.25;

L = 0.3;

g = 9.8;

Phi = zeros(2,1);

Phi(1,1) = yp(1) - y(2);

Phi(2,1) = yp(2) + (g/L)*sin(y(1));

return;

% file: ex3a_jacobian.m

function [J,M] = ex3a_jacobian(y,yp,t)

m = 0.25;

L = 0.3;

g = 9.8;

M = zeros(2,2);

J = zeros(2,2);

M(1,1) = 1;

M(2,2) = 1;

J(1,2) = -1;

J(2,1) = (g/L)*cos(y(1));

return;

6.2 System Simulation 291

% file ex3a.m

m = 0.25;

L = 0.3;

g = 9.8;

tspan = linspace(0,3,100)’;

y0 = [pi/2.0;0];

yp0 = [y0(1);-(g/L)*sin(y0(1))];

[T,Y] = ride(’ex3a_ide’,’ex3a_jacobian’,tspan,y0,yp0);

If we use q

and q

as the displacements, the Lagrange’s equations of

motion are

m¨q

+ 2λq

= 0,

m¨q

+ 2λq

− mg = 0,

+ q

− l

= 0.

(b)

The system (b) can be rewritten in state variable form using y

= q

, y

= q

= ˙q

, y

= ˙q

and y

= λ. This yields the index-3 DAEs

0 = ˙y

− y

0 = ˙y

− y

0 = m ˙y

+ 2y

0 = m ˙y

+ 2y

− mg,

0 = y

+ y

− l

(c)

Finally, we can put (c) in the GGL stabilized index-2 form (see Section 5.3.3).

This is accomplished by adding the multiplier y

and adjoining the the deriva-

tive of the displacement constraint to get

0 = ˙y

− y

+ 2y

0 = ˙y

− y

+ 2y

0 = m ˙y

+ 2y

0 = m ˙y

+ 2y

− mg,

0 = y

+ y

− l

0 = 2y

+ 2y

(d)

The m-ﬁles used to solve the system (d) are shown below. Note that in the

ﬁle ex3b.m we use the optional input DIFF INDEX to specify the diﬀerentiation

index of the variables in the system. In particular we assign diﬀerentiation

index 2 to the multipliers y

and y

. All the other variables are assigned dif-

ferentiation index 0. Also, the initial step size is set to 10

−6

in this case, since

this adjustment leads to fewer errors in the simpliﬁed Newton’s iteration.

% file ex3b_ide.m

292 6 Dynamic System Analysis and Simulation

function Phi = ex3b_ide(y,yp,t)

m = 0.25;

L = 0.3;

g = 9.8;

Phi = zeros(6,1);

Phi(1) = yp(1)-y(3)+2*y(1)*y(6);

Phi(2) = yp(2)-y(4)+2*y(2)*y(6);

Phi(3) = m*yp(3)+2*y(1)*y(5);

Phi(4) = m*yp(4)+2*y(2)*y(5)-m*g;

Phi(5) = y(1)^2+y(2)^2-L^2;

Phi(6) = y(1)*y(3)+y(2)*y(4);

return;

% file ex3b_jacobian.m

function [J,M] = ex3b_jacobian(y,yp,t)

m = 0.25;

L = 0.3;

g = 9.8;

M = zeros(6,6);

J = zeros(6,6);

M(1,1) = 1; M(2,2) = 1; M(3,3) = m; M(4,4) = m;

J(1,2) = 2*y(6); J(1,3) = -1; J(1,6) = 2*y(1);

J(2,2) = 2*y(6); J(2,4) = -1; J(2,6) = 2*y(2);

J(3,1) = 2*y(5); J(3,5) = 2*y(1);

J(4,2) = 2*y(5); J(4,5) = 2*y(2);

J(5,1) = 2*y(1); J(5,2) = 2*y(2);

J(6,1) = y(3); J(6,2) = y(4); J(6,3) = y(1); J(6,4) = y(2);

return;

% file ex3b.m

m = 0.25;

L = 0.3;

g = 9.8;

yb0 = [L;0;0;0;0;0];

ypb0 = [yb0(3);yb0(4);0;g;0;0];

options = ride_options();

options.DIFF_INDEX = [0;0;0;0;2;2];

options.INITIAL_STEP_SIZE = 1.0e-6;

[T,Yb] = ride(’ex3b_ide’,’ex3b_jacobian’,...

tspan,yb0,ypb0,options);

6.2 System Simulation 293

Some of the results from these simulations are shown in Fig. 6.3 and Fig.

6.4. Plots (i) and (ii) in Fig.6.3 show θ(t) and

θ(t), which are are computed

using the model ex3a ide. Plots (iii) through (vi) in Fig 6.3 show q

(t), q

(t),

˙q

(t), ˙q

(t), y

(t) = λ(t) and y

(t), which are are computed using the model

ex3b ide. Recall that y

is the multiplier associated with the GGL stabilized

index-2 formulation, and this variable should be zero along the solution to

the equations of motion.

The plots shown in Fig. 6.4 compare the solutions obtained using the

models ex3a ide and ex3b ide. Here, we plot the errors:

(t) = |l sin θ(t) − q

(t)|,

(t) = |l cos θ(t) − q

(t)|, and

(t) = |q

(t)

+ q

(t)

− l

where θ(t) is the result from the model ex3a ide, and q

(t), q

(t) are the

results from the model ex3b ide. The small values obtained for e

(t) and

(t) indicate that both models give essentially the same result. The small

values obtained for e

shows that the displacement constraint is satisﬁed, to

within the desired error tolerance (10

−6

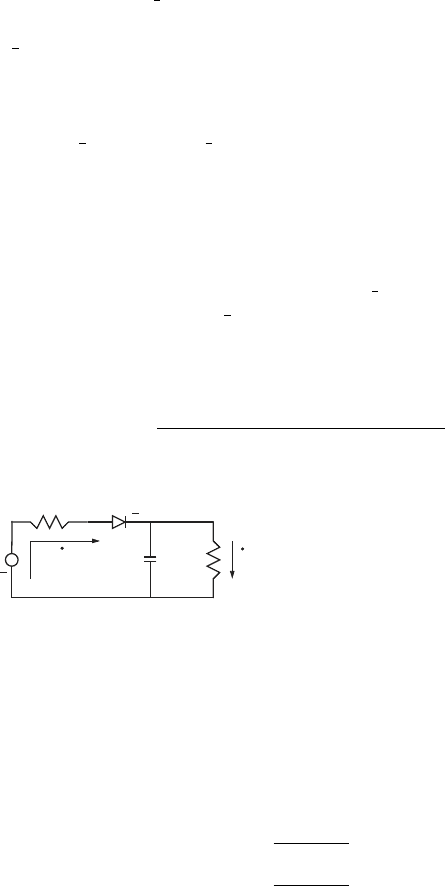
Example 6.14.

v(t)

The power supply ﬁlter shown here has

the following model parameters; R

= 8

ohm, R

= 48 ohm, C = 3900 × 10

−6

farad, and v(t) = 12 sin 120πt. Also, the

current through the diode satisﬁes ˙q

αv

−1), where the reverse saturation

current is I

= 10

−12

amp.

The thermal voltage is (1/α) = 25 × 10

−3

volt, and v

is the voltage across

the diode. Using the charges q

, q

as generalized displacements, and f

˙q

, f

= ˙q

as the corresponding ﬂows, Lagrange’s equations of motion for

this system can be written as

0 = ˙q

− f

0 = ˙q

− f

0 = R

− q

)

− v + v

0 = R

−

− q

)

0 = f

− I

αv

− 1).

(a)

We solve these equations of motion using the function ride with zero

initial conditions for all the variables, in the time interval 0 ≤ t ≤ 1. The

results of this simulation are shown in Fig. 6.5.

294 6 Dynamic System Analysis and Simulation

0 1 2 3

−2

−1

(i)

0 1 2 3

−10

−5

(ii)

dθ/dt

0 1 2 3

−0.4

−0.2

0.2

0.4

(ii)

0 1 2 3

0.1

0.2

0.3

0.4

(iv)

0 1 2 3

−3

−2

−1

(v)

/dt

0 1 2 3

−2

−1

(vi)

/dt

0 1 2 3

(vii)

0 1 2 3

−4

−2

x 10

−5

(viii)

Fig. 6.3 Example 6.13

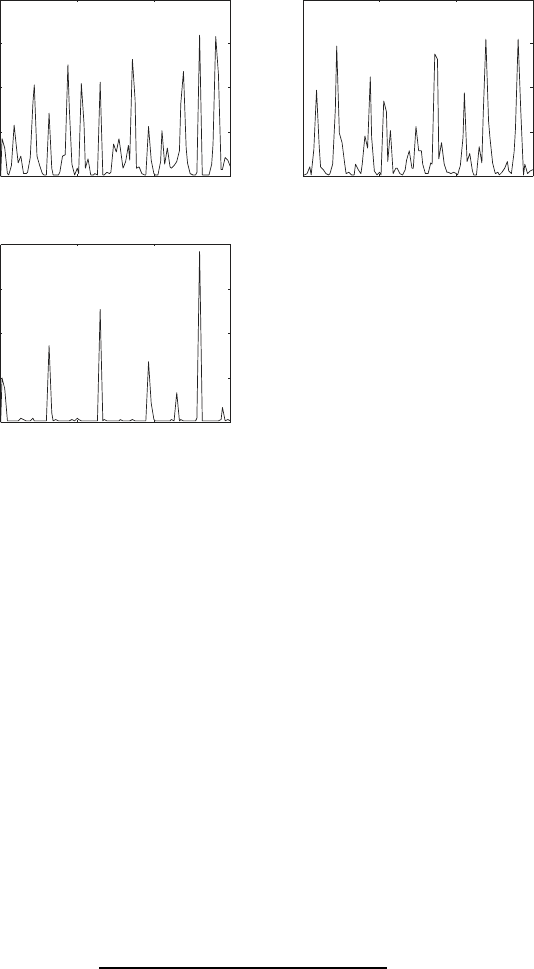
6.2 System Simulation 295

0 1 2 3

x 10

−8

(ix)

0 1 2 3

x 10

−8

(x)

0 1 2 3

x 10

−8

(xi)

Fig. 6.4 Example 6.13, continued.

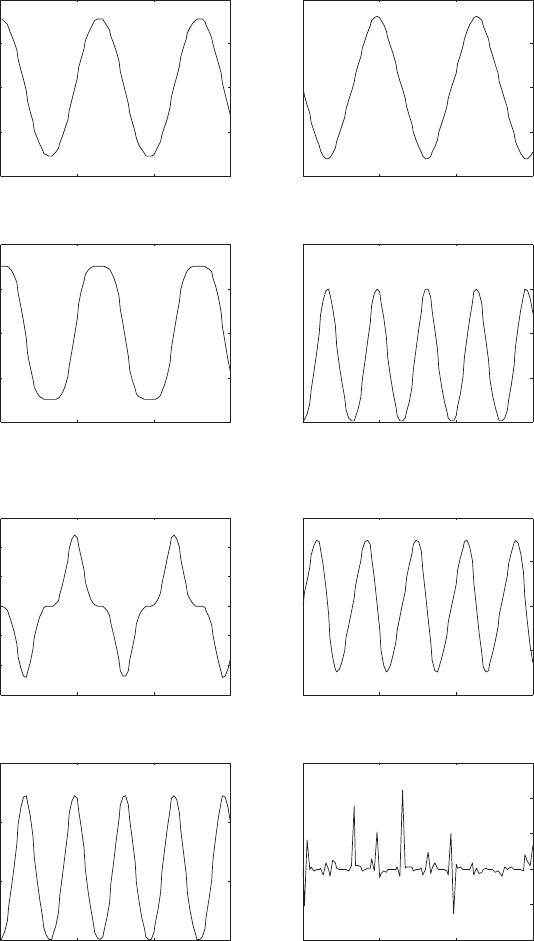
The plot (i) in Fig. 6.5 shows the voltage across the resistor R

, i.e.,

= R

. This plot covers the entire solution interval, and shows that the

system quickly approaches its steady-state response around t = 0.3 seconds.

The plot (ii) in Fig. 6.5 shows the voltage v

and the positive portion of

the input voltage v in the interval 0.9 ≤ t ≤ 1. This plot clearly shows the

variation (or ‘ripple’) in the voltage v

. The plot (iii) in Fig. 6.5 shows the

input voltage, v(t), and the voltage across the resistor R

, i.e., v

= R

Finally, the plot (iv) in Fig. 6.5 shows the input voltage, v(t), and the voltage

across the diode, i.e., v

(t).

These results clearly show the switching characteristics of the diode. In

particular, it can be seen that when the diode voltage v

attains a positive

value the current ˙q

> 0, which yields a positive voltage v

. On the other

hand, when v

< 0 we get ˙q

= 0, and hence, v

= 0. The net eﬀect is that

the diode allows positive current ﬂow when the voltage source v(t) is positive,

and no current ﬂow when v(t) is negative.

Example 6.15.

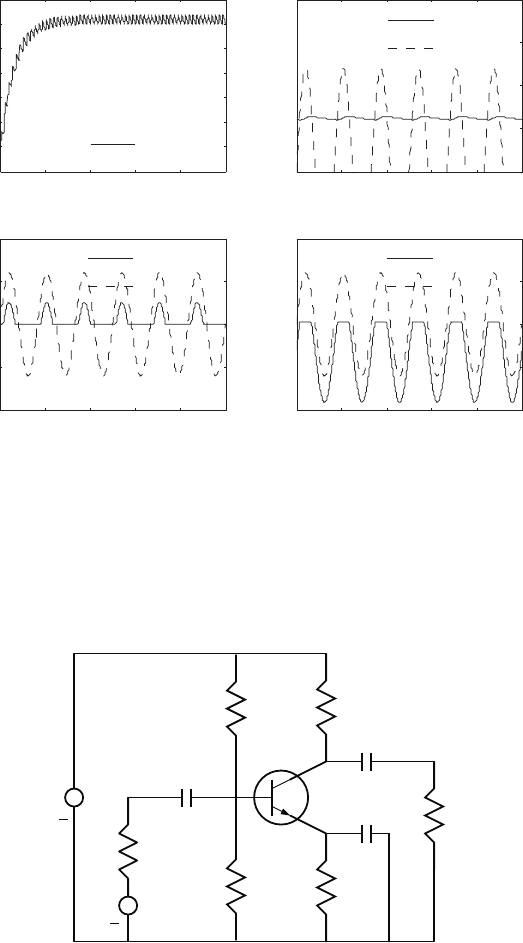
In this example we consider the modeling and simulation of the transistor

296 6 Dynamic System Analysis and Simulation

0 0.2 0.4 0.6 0.8 1

volts

(i)

0.9 0.92 0.94 0.96 0.98 1

−20

−10

volts

(iii)

0.9 0.92 0.94 0.96 0.98 1

−20

−10

volts

(iv)

0.9 0.92 0.94 0.96 0.98 1

volts

(ii)

Fig. 6.5 Example 6.14

ampliﬁer shown below. Here, the voltage source v

is constant, and provides

power to the system. The voltage source v

(t) is an input signal that is

ampliﬁed. The ampliﬁed signal drives the load resistor R

Ampliﬁer circuit

Kinematic analysis:

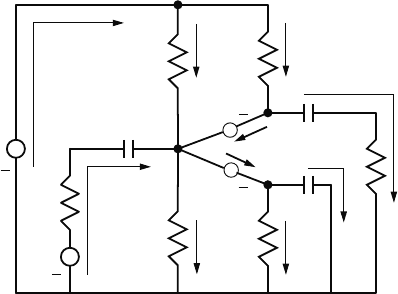
6.2 System Simulation 297

The kinematic analysis of this circuit is performed using the node and ﬂow

assignment shown in the diagram below. Here, the variables f

, f

, ···,

denote the ﬂows (i.e., the currents) in the branches of the network. The dis-

placements (i.e., the charges) corresponding to these ﬂows are q

, q

, etc.

This ﬁgure also shows an equivalent network model of the transistor. In this

model the current at the collector, f

, and emitter, f

, are determined by the

voltages v

and v

as described by the Ebbers-Moll equations





−



−I



αv

− 1

αv

− 1







, (a)

where I

, I

and I

are constants for the transistor. (See Section 1.2.5.)

Node and ﬂow assignment

This network has B = 10 branches, and N = 5 nodes (A, B, C, E and the

ground). Hence, there are 6 = B − N + 1 independent loops in the network.

Since only 6 of the branch ﬂows are independent we must construct 4 con-

straint equations to account for the ‘extra’ variables in the model. Applying

Kirchhoﬀ’s current law at nodes A, B, C and E gives the following ﬂow

constraints;

= f

− f

= 0,

= f

− f

+ f

− f

= 0,

= f

− f

= 0,

= f

− f

= 0.

(b)

These constraints can be used to eliminate 4 of the ﬂows from the model.

Here however, we will retain all ﬂow/displacement variables in the model.

Applied eﬀort analysis:

The virtual work done by the applied eﬀorts v

and v

, and the implicit

eﬀorts v

and v