Fabien B. Analytical System Dynamics: Modeling and Simulation

Подождите немного. Документ загружается.

98 2 Kinematics

References

1. H. Goldstein, Classical Mechanics, 2nd ed., Addison-Wesley, 1980.

2. D. T. Greenwood, Principles of Dynamics, 2nd ed., Prentice-Hall, 1988.

3. E. J. Haug, Intermediate Dynamics. Prentice-Hall, 1992.

4. J. L. Junkins and J. D. Turner, Optimal Spacecraft Rotational Maneuvers.

Elsevier, 1986.

5. S. W. McCuskey, Introduction to Advanced Dynamics, Addison-Wesley,

1959.

6. L. Meirovitch, Methods of Analytical Dynamics, McGraw-Hill, 1970.

7. B. Paul, Kinematics and Dynamics of Planar Machinery, Prentice-Hall,

1979.

8. G. Sandor and A. Erdman, Advanced Mechanism Design: Analysis and

Synthesis, Volume 2, Prentice-Hall, 1984.

9. A. Shabana, Computational Dynamics, John Wiley & Sons, 2001.

10. M. R. Spiegel, Theory and Problems of Theoretical Mechanics, Schaum’s

Outline Series, McGraw-Hill, 1967.

11. W. T. Thomson, Introduction to Space Dynamics, Dover Publications,

1986.

12. A. H. von Flotow and D. Rosenthal, Multi-Body Dynamics; An Algo-

rithmic Approach Based Upon Kane’s Equations. Lecture notes. MIT:

1990.

13. D. A. Wells, Theory and Problems of Lagrangian Dynamics, Schaum’s

Outline Series, McGraw-Hill, 1967.

14. J. H. Williams, Jr., Fundamentals of Applied Dynamics, John Wiley &

Sons, 1996.

15. C. E. Wilson and J. P. Sadler Kinematic and Dynamics of Machinery,

Harper Colins, 1991.

Problems

1. The cylindrical coordinates of a point are given by













1.253

4π

cos 5t

1 − cos 2t





where t denotes the time. (a) Find the position of the point using rect-

angular coordinates. (b) Plot the position and velocity of the point in

rectangular coordinates for 0 ≤ t ≤ 2π. (c) Let λ =

+ y

, where x

and y are the position of the point along the x-axis and y-axis respec-

tively. Plot λ for 0 ≤ t ≤ 2π.

2. The spherical coordinates of a point are given by

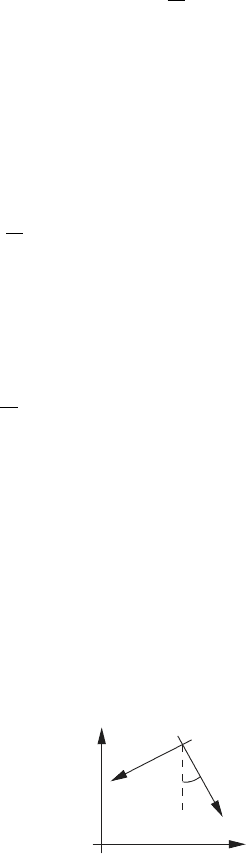
2.3 Network Systems 99













−t

3π

−2t





where t denotes the time. (a) Find the position of the point using rect-

angular coordinates. (b) Plot the position and velocity of the point in

rectangular coordinates for 0 ≤ t ≤ 2π. (c) At what value of t does the

point come to rest.

3. Consider a point that is free to move in a ﬁxed frame that is assigned

cylindrical coordinates show that the acceleration of the point is given by

¯a =

¯v = (¨ρ − ρ

) ˆe

+ (ρ

θ + 2 ˙ρ

θ) ˆe

ζ ˆe

where ρ, θ, and ζ are described in Fig. 2.1b.

4. Consider a point that is free to move in a ﬁxed frame that is assigned

spherical coordinates show that the acceleration of the point is given by

¯a =

¯v = (¨ρ − ρ

− ρ

sin

φ) ˆe

+ (2 ˙ρ

φ + ρ

φ − ρ

sin φ cos φ) ˆe

+ (2ρ

θ cos φ + 2 ˙ρ

θ sin φ + ρ

θ sin φ) ˆe

where ρ, θ, and φ are described in Fig. 2.1c.

5. Shown below are two right-handed rectangular coordinate systems x-y-

z (frame 0) and x

-y

-z

(frame 1). The origin of the x-y-z coordinate

system is Q, and the origin of the x

-y

-z

coordinate system is Q

. The

point Q

has coordinate

= [3 4.5 3.5]

with respect to the

x-y-z coordinate system, and the angle θ = 28.51

◦

(a) Find the direction cosine matrix,

, that relates the x

-y

-z

coordi-

nate system to the x-y-z coordinate system. (b) A point P has coordinate

= [0.1, 0.2, − 0.4]

with respect to the x

-y

-z

coordinate

system. Find the coordinate of the point in the x-y-z coordinate system.

100 2 Kinematics

6. Show that

in equation (2.16) and

in equation (2.17) are the

same if the rotations are small. That is, α, β, and γ are such that cos α =

cos β = cos γ = 1. Also, sin α = α, sin β = β, sin γ = γ. Moreover, terms

involving products of α, β, and γ can be neglected.

7. Suppose the orientation of the rotating frame is described by

in equa-

tion (2.16). Show that (i) (

)

(

) is skew-symmetric, and (ii) verify

that the components of the angular velocity vector satisfy equation (2.18).

8. Show that the inverse of equation (2.18) is given by equation (2.19).

9. Show that the direction cosine matrix associated with the Z

-X

-Z

Euler angles is given by





− s

−c

− s

+ c

−s

+ c

−c





where c

= cos α, s

= sin α, etc. Also, show that the angular velocities

of the x

, y

and z

axes are related to the Euler angles via the equation













−s

0 1









˙α

˙γ





10. Consider a point P that is moving in the x

-y

-z

rectangular coordinate

system as shown in Fig. 2.2. Suppose that the x

-y

-z

frame can translate

and rotate with respect to the ﬁxed rectangular coordinate system x-y-z.

Then show that the acceleration of P with respect to the ﬁxed frame is

given by

¯a =

R +

¯r +

¯α ×

¯r +

¯ω × (

¯ω ×

¯r) + 2(

¯ω ×

¯r),

where

R =

i +

j +

k is the acceleration of Q

relative to

¯r = ¨x

+ ¨y

+ ¨z

is the acceleration of P relative to Q

¯α = α

+ α

is the angular acceleration of the x

-y

-z

frame, and all other terms are deﬁned in Section 2.1.4.

11. The diagram below shows a ﬁxed rectangular coordinates system x-y-z

with origin at Q. The link QB rotates about point Q with angular velocity

that is directed along the z-axis. Moreover, QB remains in the x-y

plane. The link BC rotates about point B with angular velocity ω

that

is directed along a line perpendicular to QB. In addition, BC remains

in the plane formed by the z-axis and the line QB. The thin disk shown

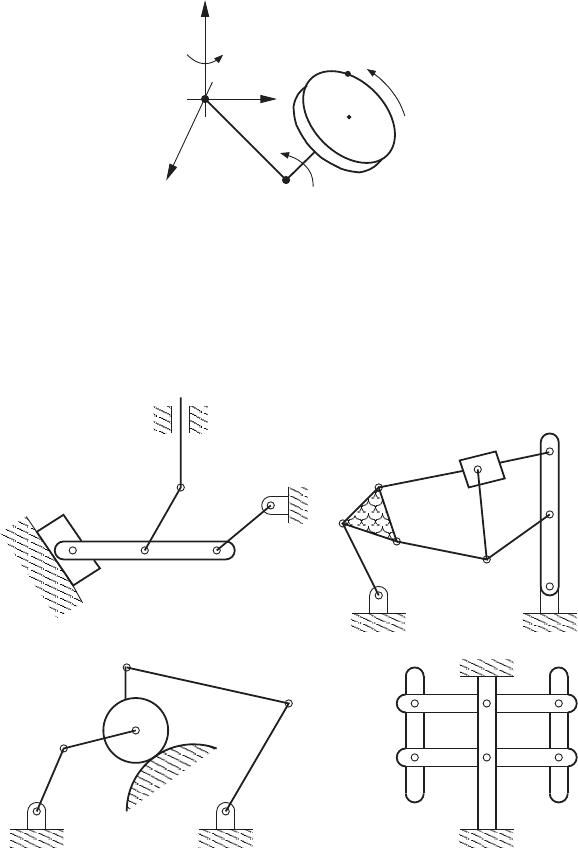
2.3 Network Systems 101

rotates about point C with angular velocity ω

that is directed along the

line BC. The radial direction of the disk is perpendicular to the line BC.

The point P is a point on the edge of the disk.

The length of QB is l

, the length of BC is l

, and the radius of the disk

is ρ. Develop a set of equations to determine the position and velocity of

point P starting from some suitable initial position.

12. For the mechanisms shown below determine; (i) the number and types of

links, (ii) the number and types of joints, and (iii) the number of degrees

of freedom.

gears

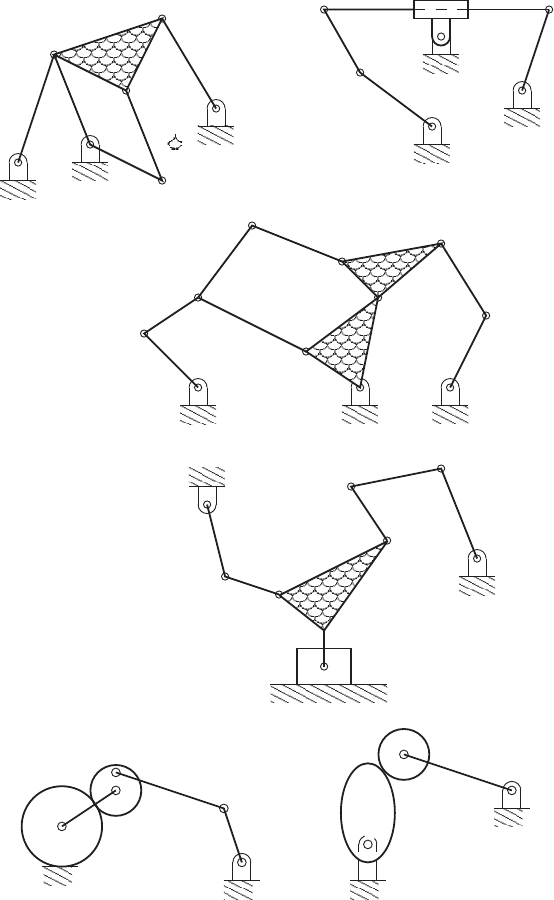
102 2 Kinematics

sliding/

gears

rolling

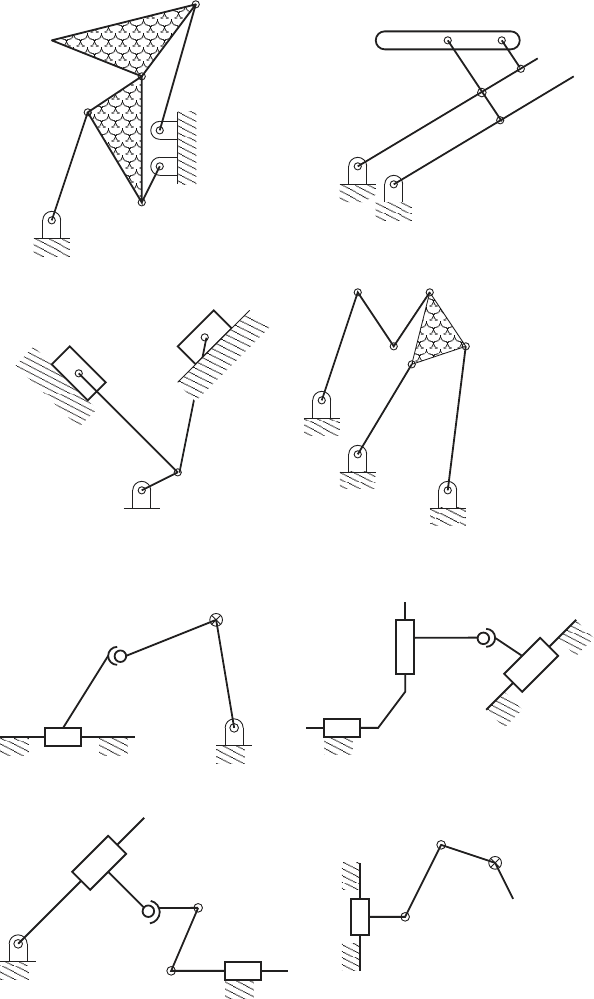
2.3 Network Systems 103

13. Find the number of degrees of freedom for the spatial mechanisms shown

below.

C S

14. For the networks shown below determine; (i) assign nodes to the system,

(ii) determine the number of branches, (iii) determine the number of

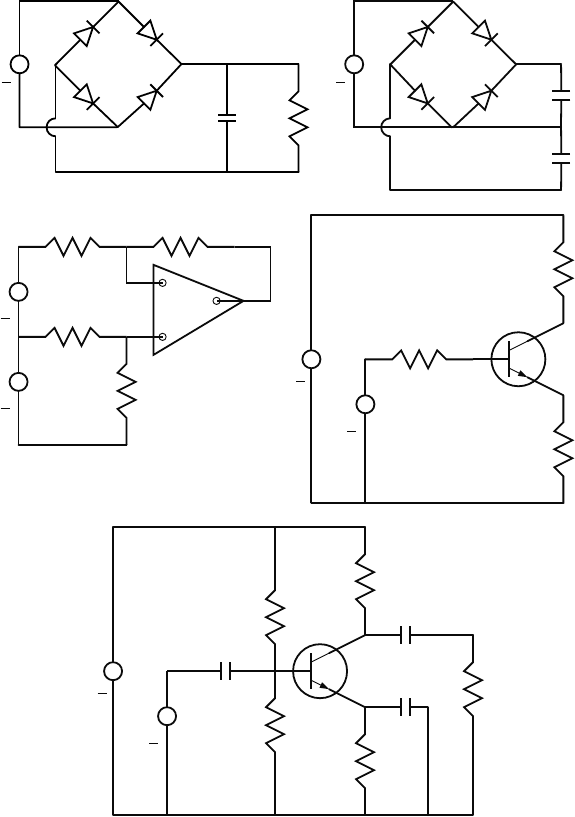
104 2 Kinematics

independent loops, (iv) assign ﬂows to the branches, and (iv) write ﬂow

constraint equations for the nodes.

C R

R R

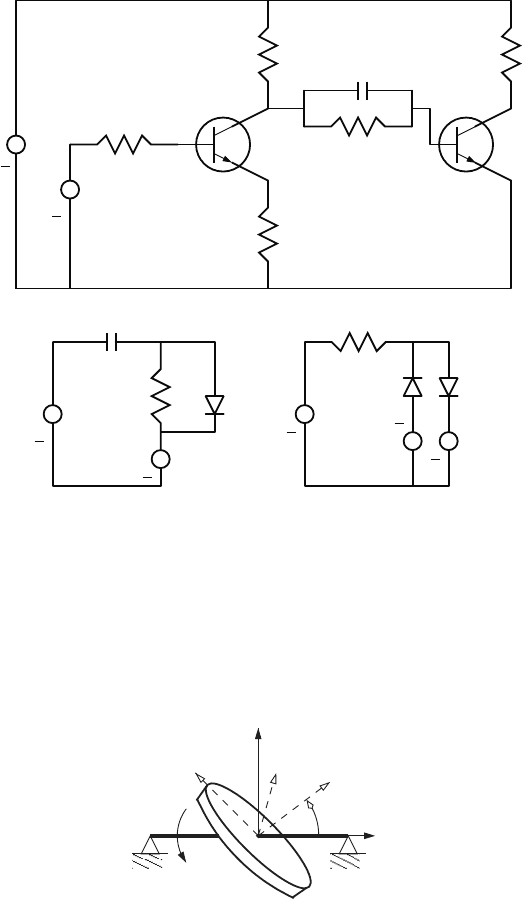
2.3 Network Systems 105

v v

15. In the system shown below x-y-z represents the ﬁxed rectangular coordi-

nate system. The disk shown is attached to the shaft AB, and the shaft

has a constant angular velocity, ω

, about the ﬁxed z-axis. The princi-

pal axes of inertia for the disk are aligned with the x

-y

-z

rectangular

coordinate system, which is embedded in the disk. The z

-axis make a

constant angle α with the z-axis. Find an expression for the angular veloc-

ity of the disk. Speciﬁcally, determine ¯ω = ω

+ω

, where

and

are the unit vectors in the x

, y

and z

directions respectively.

16. The disk shown below has radius r, and it rolls without slipping on the

horizontal plane. The angular velocity of the disk is ω = 2π rad/s.

a. Compute and plot the position, velocity and acceleration of a point P

that is on the edge of the disk.

b. What is the velocity and acceleration of P when P is in contact with

the ground?

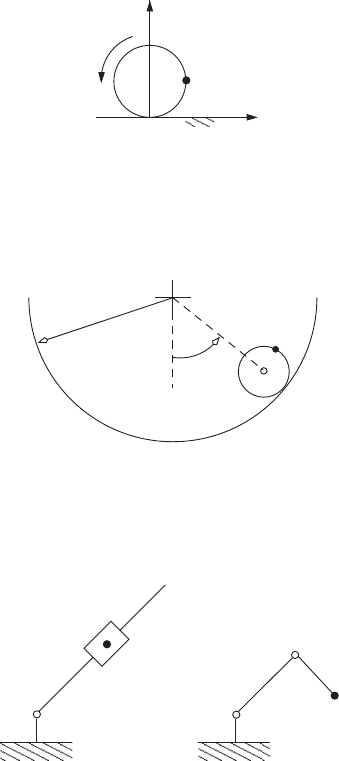
106 2 Kinematics

17. A disk with radius r rolls with out slipping on the inside of a cylinder

that has a radius R. Determine the position and velocity the the point

C on the edge of the disk, if the disk rotates around the cylinder with

constant angular velocity

θ = 2π radians/second.

18. Develop the equations that determine the position and velocity of the

point C on the robots shown below. The robot shown in (a) moves in a

plane and has a revolute joint and a prismatic joint. The robot shown in

(b) has a spherical joint at A an a revolute joint at B.

(b)

(a)

19. The ﬁgure below shows a planar R-P robot. The point A on the end

eﬀector moves from (x = 3, y = −3) to (x = 3, y = 3) along a straight

line in 3 seconds. The motion is such that A starts at rest and ends at rest.

a. Select an appropriate trajectory for the coordinates x

(t), and y

(t),

for 0 ≤ t ≤ 3.

b. Given x

(t) and y

(t), compute r(t), ˙r(t), ¨r(t), θ(t),

θ(t) and

θ(t).

c. Plot these variables versus time.

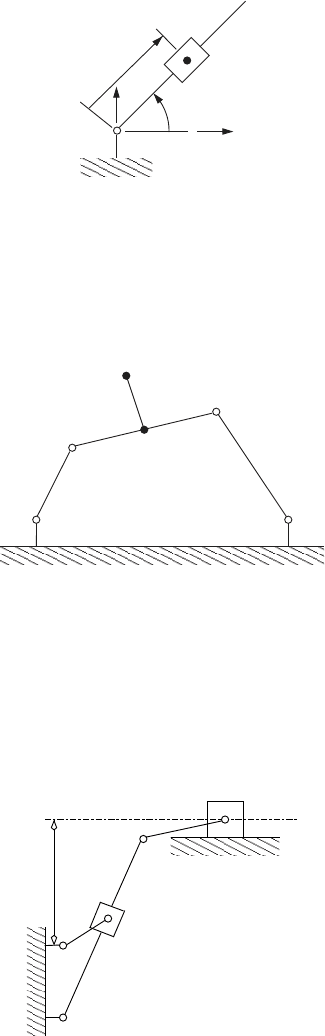
2.3 Network Systems 107

20. The fourbar mechanism shown below has the following proportions:

AD = 2.5, AB = 1, BC = 4, DC = 2, BE = 2, and EF = 0.75.

Note that EF is perpendicular to BC. The crank AB has an angular

velocity of 2π radians/second counterclockwise. Find the equations re-

quired to compute the position and velocity of the point F. Plot the path

of the point F , and its velocity.

21. The quick return mechanism shown below has revolute joints at A, B,

C, E, and F , and prismatic joints at D and G. The proportions of the

mechanism are as follows: AB = 4 cm, BC = 2 cm, AE = 8 cm, and

EF = 3 cm. If the crank, BC, has angular velocity 2π radians/second

ﬁnd the equations required to compute the the position and velocity of

the point F as a function of the crank angle. Plot the conﬁguration of the

mechanism for crank angles 0, 0.2π, 0.4π, ···, 1.8π radians. Also, plot the

velocity of F , the angular velocity of AE, and the angular velocity of EF .