Fabien B. Analytical System Dynamics: Modeling and Simulation

Подождите немного. Документ загружается.

108 2 Kinematics

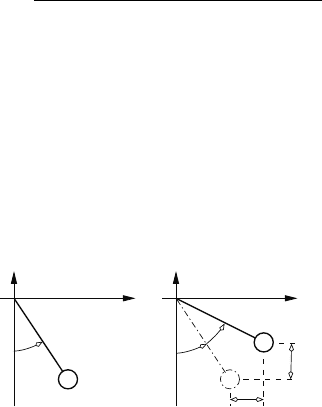
22. The mechanism shown below has revolute joints at A, B, and C, and the

disk rolls on the ground without slipping at E. Find the equations neces-

sary to determine the conﬁguration of the mechanism at all times. If the

crank has an angular velocity 2π radians/second, determine the position

and velocity of the points C and D (the center of the disk). The mech-

anism has the following proportions: QA = 0.5, AB = 1.0, BC = 5.0,

CD = 2.5, and r = 3.

23. The mechanism shown below is an R-C robot. The link AD is connected

to the ground at A via a revolute joint. Moreover, the rotation at A takes

place about an axis that is perpendicular to the page. The link BE is

connected to the link AB via a cylindrical joint at B. The link BE can

translate along the line AD, and rotate about the line AD. Find a set of

equations to determine the position and velocity of the point E.

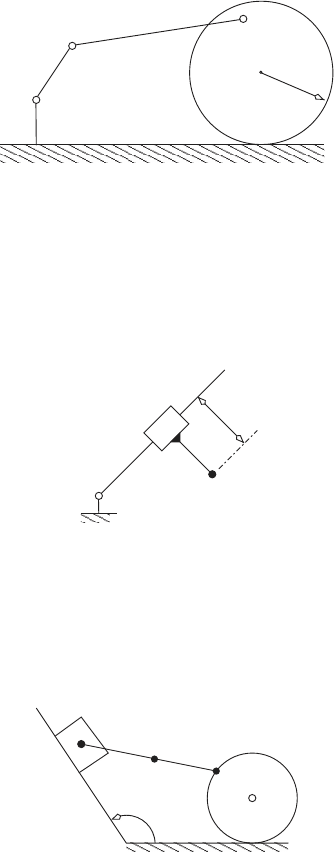
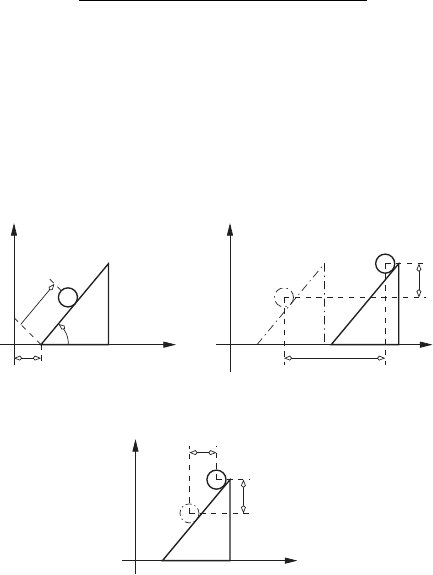
24. Determine the equations required to compute the position and velocity of

the point D on the mechanism shown here. The slider A stay in contact

with the wall while the disk CB rolls without slipping. The link AB is

attached to the slider via a revolute joint at A, and it is attached to the

disk via a revolute joint at B. Use the following dimensions: AB = l,

AD = d, and CB = r is the radius of the disk. The angle α is ﬁxed.

Chapter 3

Lagrange’s Equation of Motion

This chapter develops Lagrange’s equation of motion for a class of multi-

discipline dynamic systems. To derive Lagrange’s equation we utilize some

concepts from analytical dynamics, and the ﬁrst law of thermodynamics. By

carrying out the development using the fundamental variables it is clear that

the results obtained are applicable to all the engineering disciplines described

in Chapter 1.

Section 3.1 introduces the concepts of generalized displacement, virtual

displacement and virtual work. In Section 3.2 Lagrange’s equation of motion

is derived starting from the ﬁrst law of thermodynamics. In Section 3.3 vari-

ous examples are used to illustrate the application of Lagrange’s equation to

mechanical, electrical, ﬂuid, and multidiscipline systems.

3.1 Analytical Dynamics

As discussed in Chapter 1 dynamic systems can be described as an assemblage

of inductors, capacitors, resistors, constraint elements and sources. Associated

with each of these elements is the set of fundamental variables displacement,

q, ﬂow, f, eﬀort, e, and momentum, p. From Paynter’s diagram (Fig. 1.4)

it can be observed that all four variables are not all required to determine

the state of the system at any time. In fact only two of the fundamental

variables are required to determine the states of the system since, the other

two variables can be determined using the system properties and the diﬀer-

ential/integral relationship between the variables.

In Lagrangian dynamics the displacement and ﬂow variables are used to

describe the system behavior. In the Hamiltonian description of dynamic

systems the momentum and displacement variables are used to describe the

system. The bond graph and linear graph description of dynamic systems use

the eﬀort and ﬂow variables to describe the system behavior.

B. Fabien, Analytical System Dynamics: Modeling and Simulation, 109

DOI 10.1007/978-0-387-85605-6 3,

 Springer Science+Business Media LLC 2009

110 3 Lagrange’s Equation of Motion

3.1.1 Generalized variables

The number of displacement and ﬂow variables that can be assigned to a dy-

namic system can be quite large. However, for each system there is a minimum

number of displacement variables that are required to uniquely determine the

state or conﬁguration of the system. This minimum set of displacement vari-

ables are called the generalized displacements. The corresponding set of ﬂow

variables are called the generalized ﬂows. The number of generalized dis-

placement variables used to the describe the system is equal to the number

of degrees of freedom. (See Section 2.2 and Section 2.3.)

Example 3.1.

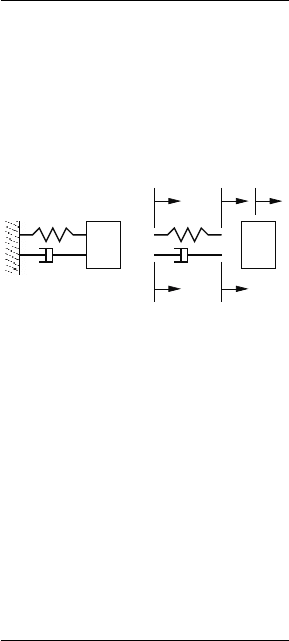
Consider the spring, mass damper system shown in Figure 3.1a. Figure

3.1b shows the displacement coordinates assigned to the system components.

Assigned to the mass is the displacement, x

. The left and right end of the

(b)

x x

(a)

Fig. 3.1 Spring-mass-damper

spring are assigned displacement variables x

, and x

, respectively. The left

and right end of the damper are assigned displacement variables x

, and x

respectively Since the left end of the spring and damper are ﬁxed, it is clear

that x

= x

= 0. Also, since the right ends of the spring and damper are

attached to the mass we have x

= x

. Thus, the system can be de-

scribed using the single displacement variable x

, and the the corresponding

ﬂow variable v

. This system has 1 degree of freedom with x

being the the

generalized displacement and v

the corresponding generalized ﬂow.

Example 3.2.

Figure 3.2a shows a resistor, R, an inductor, L, and a capacitor, C, in series

with a voltage source, v. Figure 3.2b shows the ﬂow variables assigned to the

system components. The current i

is assigned to the voltage source, i

the resistor, i

to the inductor, and i

to the capacitor. However, Kirchhoﬀ’s

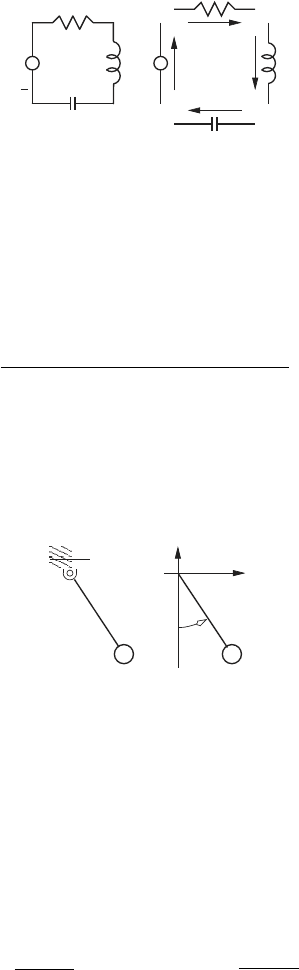
3.1 Analytical Dynamics 111

(a)

(b)

Lv i

Fig. 3.2 Resistor-inductor-capacitor

current law states that the currents ﬂowing into a node must sum to zero. As

a result, i

= i

, i

= i

, i

= i

, and i

= i

. Thus, the system has 1 degree

of freedom (and only one ﬂow variable is required). We can select i

as the

generalized ﬂow variable, with q

dt as the generalized displacement.

Example 3.3.

Figure 3.3a shows a simple pendulum. In this system the mass, m, is at-

tached to an inertialess rod of length l. The rod rotates freely about point

(x,y)

(b)(a)

Fig. 3.3 Simple pendulum

The conﬁguration of the system can be described using the displacement

variables x and y. However, these variables are not independent. Since the

rod is rigid we must satisfy the displacement constraint

φ = x

+ y

− l

= 0. (a)

This displacement constraint can be used to eliminate x or y as follows:

x = ±

− y

(b), y = ±

− x

(c).

Unfortunately, the transformation (b) gives an ambiguous result when y = 0,

and the transformation (c) gives an ambiguous result when x = 0.

Alternatively, the angle θ can be used to establish that

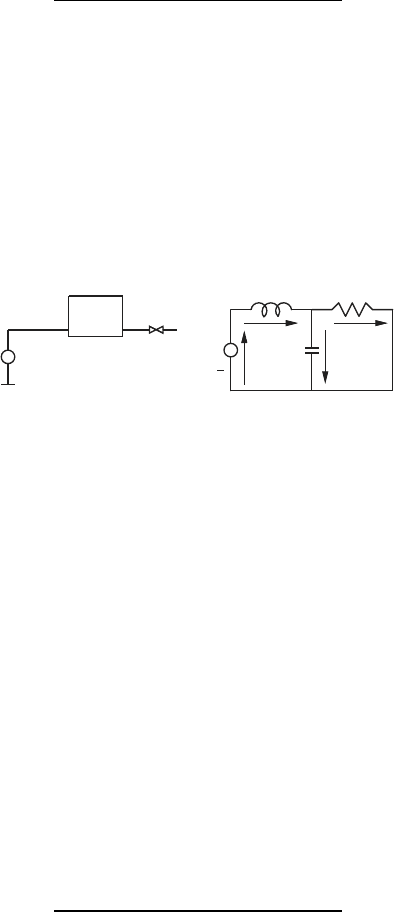
112 3 Lagrange’s Equation of Motion

= x − l sin θ = 0 (d), φ

= y + l cos θ = 0 (e).

Thus, if θ is known we can unambiguously determine x and y using the

constraints φ

and φ

Clearly, this system has 1 degree of freedom, and we can select θ as the

generalized displacement, with

θ as the generalized ﬂow.

Example 3.4.

Figure 3.4a shows a hydraulic system consisting of a pump that delivers

ﬂuid at a desired pressure to a long pipe. The pipe is connected to a storage

tank which is in turn connected to a valve. A schematic of a model for the

system is shown in Fig. 3.4b. The model has an eﬀort source P for the pump,

the inertia of the ﬂuid in the long pipe is model using L

, the capacitance of

the tank is included in C

, and the resistance of the valve is modeled using

. The ﬂow variables that describe the conﬁguration of the system are Q

(a) (b)

Pump

Tank

Valve

Long

pipe

Fig. 3.4 Hydraulic system

the volume ﬂow through the pump, Q

the volume ﬂow through the pipe,

the volume ﬂow stored in the tank, and Q

the volume ﬂow through the

valve.

These four ﬂow variables are not independent. Since there are no leaks in

the system, the continuity of ﬂow requires that at node A,

= Q

− Q

= 0, (a)

and at node B,

= Q

− Q

= 0. (b)

Equations (a) and (b) represent ﬂow constraints that must be satisﬁed. These

two equations can be used to eliminate two of the ﬂow variables. Thus, the

system has 2 degrees of freedom. (Only two of the four variables are indepen-

dent.) Suppose we select Q

and Q

as the generalized ﬂow variables. Then,

from (a) and (b) we get Q

= Q

and Q

= Q

− Q

, respectively.

3.1 Analytical Dynamics 113

From the examples above it can be observed that a system can be described

by N conﬁguration coordinates say, u

, u

, ···, u

, that are diﬀerent form the

n generalized displacements q

, q

, ···, q

. Here, n is the number of degrees

of freedom, and N ≥ n. Moreover, the n generalized displacements are all

independent.

3.1.2 Virtual displacements

A virtual displacement is a small displacement of the system that is (i) con-

sistent with the constraints, and (ii) takes place contemporaneously. It is the

second requirement that distinguishes virtual displacements from diﬀerential

displacements. (Here, a diﬀerential displacement a small displacement of the

system that is consistent with the constraints.)

To clarify the diﬀerence between diﬀerential displacements and virtual

displacements consider the following examples.

Example 3.5.

Figure 3.5a shows a simple pendulum with conﬁguration displacements x

and y, and generalized displacement θ. From Example 3.3 we know that the

system satisﬁes the two displacement constraints

= x − l sin θ = 0, φ

= y + l cos θ = 0.

Now, suppose the system undergoes a small displacement dθ that takes place

(x,y)

θδ

δd

= y

lθ

(a) (b)

(x,y)

Fig. 3.5 Virtual displacement: simple pendulum

over the time interval dt as shown in Fig. 3.5b. Then, the diﬀerential of the

constraints gives

dφ

= dx − (l cos θ)dθ = 0, dφ

= dy − (l sin θ)dθ = 0.

114 3 Lagrange’s Equation of Motion

Hence, for a diﬀerential displacement dθ, the conﬁguration displacements that

are consistent with the constraints are dx = (l cos θ)dθ and dy = (l sin θ)dθ.

A virtual displacement is the same as a diﬀerential displacement but with

time held ﬁxed, i.e., dt = 0. Let δθ denote a virtual displacement of the

generalized displacement θ, δx denote a virtual displacement of x, and δy

denote a virtual displacement of y. Then the variation of the constraints

gives

δφ

= δx −(l cos θ)δθ = 0, δφ

= δy − (l sin θ)δθ = 0.

Thus, in this case the virtual displacements and the diﬀerential displacements

are the same. Also, note that a variation is similar to a diﬀerential but with

time held ﬁxed.

Example 3.6.

Figure 3.6a shows a particle that is constrained to move along a ramp that

has a ﬁxed incline α. The ramp is free to move along the x-axis, and its

position is given by X = A sin ωt, where A and ω are constants, and t is the

time. The conﬁguration displacements for the system are x and y, and the

generalized displacement is r. From the geometry of the system we get the

(x,y)

(a)

(b)

(c)

Fig. 3.6 Virtual displacement: moving ramp

two displacement constraints

= x − A sin ωt −r cos α = 0,

= y − r sin α = 0.

3.1 Analytical Dynamics 115

Now, suppose the system undergoes a small displacement, dr, that takes

place over the time interval dt as shown in Fig. 3.6b. Then, the diﬀerential

of the constraints gives

dφ

= dx − (Aω cos ωt)dt −dr cos α = 0,

dφ

= dy − dr sin α = 0.

On the other hand if the system undergoes a virtual displacement, δr,

then, the variation of the constraints gives

δφ

= δx −δr cos α = 0,

δφ

= δy − δr sin α = 0.

This variation is illustrated in Fig. 3.6c. In this case the diﬀerential displace-

ment dx, and the virtual displacement δx are not the same. This is due to the

fact that the constraint surface is moving, i.e., the constraint depends explic-

itly on time. Note also that the variation of the constraints can be obtained

from the diﬀerential of the constraints by setting dt = 0.

3.1.3 Virtual work

The virtual work is the work done by the eﬀorts in carrying the system

through a virtual displacement, i.e.,

δW =

i=1

δq

. (3.1)

Here, δW is the virtual work, δq

are the virtual displacements, e

are the

applied eﬀorts, and i = 1, 2, ···, n with n being the number of degrees of

freedom. Note that q

are the generalized displacements, and e

are the cor-

responding generalized eﬀorts. The virtual work is also equal to the work

done by the ﬂows in carrying the system through a virtual momentum, i.e.,

δW =

i=1

δp

, (3.2)

where δp

are the virtual momentum, and f

are the ﬂows. Equations (3.1)

and (3.2) follow from the deﬁnitions of the increment in work, i.e., equations

(1.3) and (1.4), respectively.

An important consequence of the deﬁnition of virtual work is that con-

straint eﬀorts do not contribute to the virtual work. This is most easily

illustrated via an example.

116 3 Lagrange’s Equation of Motion

Example 3.7.

Figure 3.7a shows a mass, m, that is free to slide on a smooth ramp un-

der the inﬂuence of the acceleration due to gravity, g. The ramp is ﬁxed

and has a ﬁxed slope with angle α. A free body diagram for the mass is

(a)

(b)

Fig. 3.7 Virtual work: constraint eﬀort

shown in Fig. 3.7b. Here, the weight acts downward, and the reaction force

(i.e., the constraint eﬀort), R, acts perpendicular to the ramp as shown. The

conﬁguration displacements for the system are x and y.

The virtual work done by all the eﬀorts acting on the mass is

δW = −mg δy + R cos α δy − R sin α δx. (a)

The mass is constrained to move along the ramp. Thus,

φ = y − x tan α, (b)

is a displacement constraint that must be satisﬁed. The variation of this

constraint gives

δφ = δy − δx tan α = 0. (c)

Using (c) in (a) gives

δW =



−mg + R cos α − R

sin α

tan α



δy

δW = −mg δy

Therefore, the constraint force, R, does no virtual work on the system.

The result obtained in Example 3.7 can be shown to be true in general.

In fact the constraint eﬀorts are all perpendicular to the constraint surface,

while the virtual displacements take place tangent to the constraint surface.

Hence, the constraint eﬀorts will make no contribution to the virtual work.

3.2 Lagrange’s Equations of Motion 117

In many cases the applied eﬀorts are given in terms of the conﬁguration

displacements instead of the generalized displacements. Such situations re-

quire that we use the relationship between the conﬁguration and generalized

displacements to ﬁnd expressions for the generalized eﬀorts. In particular,

suppose u

are the conﬁguration displacements, and E

are the correspond-

ing conﬁguration eﬀorts, for i = 1, 2, ···, N. Let q

be the generalized dis-

placements, and e

be the corresponding generalized eﬀorts. Then, there are

transformation equations of the form

= U

, q

, ···, q

) (3.3)

that relate the conﬁguration and generalized displacements (see the examples

above).

The virtual work done by the applied eﬀorts satisﬁes

δW =

i=1

δu

i=1

δq

But from (3.3) it can be seen that the virtual displacements δu

satisfy

δu

j=1

∂U

∂q

δq

Hence,

δu

= E

j=1

∂U

∂q

δq

which yields

j=1

∂U

∂q

. (3.4)

We will make use of this result in several of the examples to follow.

3.2 Lagrange’s Equations of Motion

In this section we develop Lagrange’s equation of motion for unconstrained

systems. By an unconstrained system we mean that the displacements used to

describe the system are independent hence, they represent a set of generalized

displacements. Constrained systems will be discussed in Chapter 4.

The ﬁrst law of thermodynamics can be written as

An alternate derivation of Lagrange’s equation of motion, for multidiscipline systems, can

be developed by invoking Hamilton’s principle of least action. See for example, Wellstead

(1979); White and Woodson (1959); and Williams (1996).