Fabien B. Analytical System Dynamics: Modeling and Simulation
Подождите немного. Документ загружается.


138 3 Lagrange’s Equation of Motion
Before leaving this example it will prove instructive to reexamine the ki-
netic coenergy of the link AB. In the analysis above the link AB is treated
as a rigid body in general plane motion. Hence, equation (3.14) is used to
determine the kinetic coenergy of the link as
T
∗
AB
=
1
2
m
1
¯v
1
· ¯v
1
+
1
2
I
1
˙α
2
=
1
2
I
1
+
m
1
l
2
1
4
˙α
2
, (f)
where m
1
is the mass of the link, ¯v
1
is the velocity of the center of mass of
the link, I
1
is the moment of inertia about the center of mass, and ˙α is the
angular velocity of the link.
However, the link AB can also be treated as a rigid body rotating about
a fixed point, i.e., link AB rotates about the fixed point A. In which case the
kinetic coenergy of the link AB is given by equation (3.15) as
T
∗
AB
=
1
2
I
1
A
˙α
2
, (g)
where I
1
A
is the moment of inertia of the link AB about point A. Comparing
equations (f) and (g) it is evident that
I
1
A
= I
1
+ m
1
l
2
1
4
.
Which is in fact the result one would obtain by applying the parallel axis
theorem. It is then clear that we can replace equation (f) with with (g) in
T
∗
, and obtain the same differential equations of motion.
Example 3.15.
A model of a symmetric top is shown in the figure below. Here, the top
is free to rotate about a fixed point Q. The rectangular coordinate system
x-y-z represents the fixed reference frame for the system. The rectangular
coordinate system x
1
-y
1
-z
1
is attached to the top at the point Q such that
the z
1
-axis is along the line from Q to C. The point C is the center of mass
for the top, and l is the distance from Q to C. The mass of the top is m. The
moments of inertia about the point Q are I
12
, I
12
, and I
3
in the x
1
, y
1
, and
z
1
directions, respectively. (Note that the moments of inertia are given with
respect to the fixed point Q, not the center of mass.) The acceleration due to
gravity acts downward as shown. The dynamic equations of motion for this
system can be developed as follows.
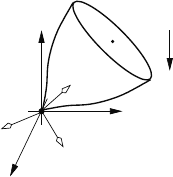
3.3 Applications 139
g
x
y
1
z
1
z
y
x
Q
C
1
Kinematic analysis:
Since the top is free to rotate in about the point Q the system has 3 degrees of
freedom, i.e., the variables that determine the direction cosine matrix of the
x
1
-y
1
-z
1
coordinate system. Here, the orientation of the x
1
-y
1
-z
1
coordinate
system with respect to the fixed frame will be described using the Z
α
-X
β
-Z
γ
Euler angles (see Section 2.1.5). A point r = [x, y, z]
T
in the x-y-z coor-
dinate system is then related to a point
1
r = [x
1
, y
1
, z
1
]
T
in the x
1
-y
1
-z
1
coordinate system via the equation
r =
0
A
1
1
r, (a)
where the direction cosine matrix is
0
A
1
=
c
α
c
γ
− s
α
c
β
s
γ
−c
α
s
γ
− s
α
c
β
c
γ
s
α
s
β
s
α
c
γ
+ c
α
c
β
s
γ
−s
α
s
γ
+ c
α
c
β
c
γ
−c
α
s
β
s
β
s
γ
s
β
c
γ
c
β
.
Here, c
α
= cos α, s
α
= sin α, etc. The angles α, β and γ are taken as the
generalized displacements, and ˙α,
˙
β and ˙γ are the corresponding generalized
flows.
Let ω
1
, ω
2
and ω
3
be the angular velocities of the x
1
-axis, y
1
-axis, and
z
1
-axis, respectively. Then, ω
1
, ω
2
and ω
3
are related to the Euler angles via
the equation
ω
1
ω
2
ω
3
=
s
β
s
γ
c
γ
0
s
β
c
γ
−s
γ
0
c
β
0 1
˙α
˙
β
˙γ
. (b)
(See Problem 9 in Chapter 2.)
Applied effort analysis:
The virtual work done by the weight of the top is δW = −mg δz
C
where
δz
C
is the variation in the position of the center of mass, C, along the z-
axis. The coordinate of C in the x
1
-y
1
-z
1
system is
1
r
C
= [0, 0, l]
T
. Using
equation (a) it can be seen that the coordinate of C in the x-y-z system is
140 3 Lagrange’s Equation of Motion
r
C
=
x
C
y
C
z
C
=
0
A
1
1
r
c
=
ls
α
s
β
−lc
α
s
β
lc
β
.
Therefore, δz
C
= −ls
β
δβ, and the virtual work due to the weight is
δW = mgls
β
δβ.
Which gives the generalized efforts as e
s
α
= 0, e
s
β
= mgls
β
, and e
s
γ
= 0.
Lagrange’s equation:
The kinetic coenergy of the top is
T
∗
=
1
2
(I
12
ω
1
2
+ I
12
ω
2
2
+ I
3
ω
3
2
) =
1
2
I
12
h
s
2
β
˙α
2
+
˙
β
2
i
+
1
2
I
3
(c
β
˙α + ˙γ)
2
.
For this system the potential energy is V = 0, and the dissipation function
is D = 0.
Lagrange’s equations for the system are
d
dt
∂T
∗
∂ ˙α
−
∂T
∗
∂α
+
∂D
∂ ˙α
+
∂V
∂α
= e
s
α
,
d
dt
∂T
∗
∂
˙
β
−
∂T
∗
∂β
+
∂D
∂
˙
β
+
∂V
∂β
= e
s
β
,
d
dt
∂T
∗
∂ ˙γ
−
∂T
∗
∂γ
+
∂D
∂ ˙γ
+
∂V
∂γ
= e
s
γ
.
Using T
∗
, V , and D it can be shown that these yield the differential equations
d
dt
(I
12
s
2
β
+ I
3
c
2
β
) ˙α + I
3
c
β
˙γ
= 0,
I
12
¨
β − [I
12
− I
3
] s
β
c
β
˙α
2
+ I
3
s
β
˙α ˙γ = mgls
β
,
d
dt
[I
3
(c
β
˙α + ˙γ)] = 0.
3.3.2 Electrical systems
The application of Lagrange’s equation to electrical systems can be accom-
plished using the following procedure.
1. Kinematic analysis.
3.3 Applications 141
The electrical systems considered here form a network of elements, i.e.,
ideal inductors, capacitors and resistors. Each system element forms a
branch of the network, and the interconnection between the elements de-
fine the nodes of the network. A simple approach to modeling these systems
is to assign a flow variable (i.e., a current) to each branch of the network.
This will usually result in a large number of variables that are not all inde-
pendent. In fact, if B is the number of branches in the network, and N is
the number of nodes in the network, then the number of independent flow
variables will be n = B − N + 1. Equations relating the dependent vari-
ables to the independent variables can be obtained by applying Kirchhoff’s
current law at the nodes of the network.
2. Applied effort analysis.
The virtual work done by all effort (i.e., voltage) sources must be defined
in terms of the generalized displacements. Here, the virtual work done by
an effort source is positive if the current flows from the negative terminal
to the positive terminal of the source.
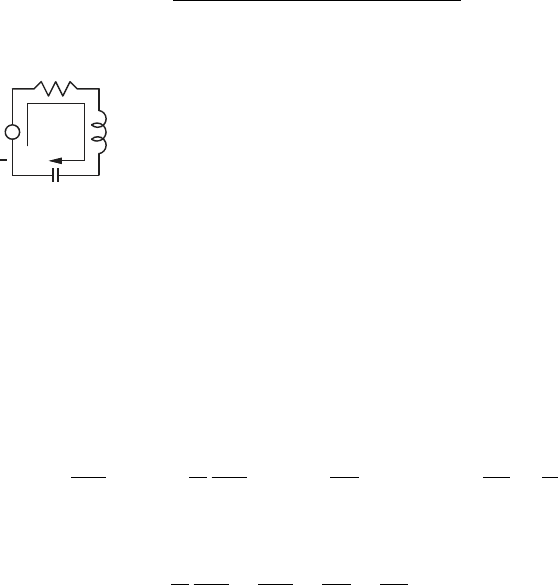
Example 3.16.
i
+
R
C
Lv
RLC circuit
The RLC (resistor R, inductor L, capacitor C) shown here
has an applied voltage v. The dynamic analysis of this
system using Lagrange’s equation proceeds as follows.
The current, i = dq/dt = ˙q, is selected as the generalized
flow variable, and q is the corresponding charge (i.e., the
generalized displacement).
Applied effort analysis:
The virtual work done by the voltage is δW = v δq = e
s
q
δq.
Therefore, the generalized effort is e
s
q
= v.
Lagrange’s equation:
The kinetic coenergy, potential energy and the dissipation function are
T
∗
= L ˙q
2
/2, V = q
2
/(2C), and D = R ˙q
2
/2, respectively. Using these func-
tions we have the following results:
∂T
∗
∂ ˙q
= L ˙q,
d
dt
∂T
∗
∂ ˙q
= L¨q,
∂D
∂ ˙q
= R ˙q, and
∂V
∂q
=
q
C
.
Hence, Lagrange’s equation for this system is
d
dt
∂T
∗
∂ ˙q
−
∂T
∗
∂q
+
∂D
∂ ˙q
+
∂V
∂q
= e
s
q
,
142 3 Lagrange’s Equation of Motion
L¨q + R ˙q +
q
C
= v.
This second order ordinary differential equation describes the behavior of the
system in terms of the charge q. This equation can be rewritten in terms of
the current as
L
di
dt
+ Ri +
1
C
Z
i dt = v.
Example 3.17.
A model of an electrical lead filter with applied voltage v is shown in the
figure below. The dynamic equations of motion for this system can be deter-
mined as follows.
C
q
3
q
0
+ C
v
q
q
A B
2
1
R
1
R
2
Kinematic analysis:
The circuit has four branches and three nodes (i.e., A, B and C). A current
is assigned to each branch of the network. The system has n = B −N + 1 =
4 − 3 + 1 = 2 degrees of freedom. (Recall that B is the number of branches
and N is the number of nodes in the network.) Therefore, only two of the
four flows ˙q
0
, ˙q
1
, ˙q
2
, ˙q
3
are independent. Here, we select q
1
and q
3
as the in-
dependent (generalized) displacements. The corresponding generalized flows
are ˙q
1
and ˙q
3
.
Applying Kirchhoff’s current law to nodes B and C gives the relationships
˙q
2
= ˙q
3
− ˙q
1
, and ˙q
0
= ˙q
3
, respectively. Hence, we have obtained explicit
expressions for the dependent flows in terms of the independent flows. More-
over, integrating the first of these equations leads to q
2
= q
3
−q
1
+ q
20
, where
q
20
is the initial charge in the capacitor.
Applied effort analysis:
The virtual work done by the voltage source is δW = v δq
0
= v δq
3
=
e
s
q
1
δq
1
+ e
s
q
3
δq
3
. Therefore, the generalized efforts are e
s
q
1
= 0, and e
s
q
3
= v.
Lagrange’s equations:
The kinetic coenergy, potential energy and the dissipation function are
T
∗
= 0, V = (q
3
− q
1
+ q
20
)
2
/(2C), and D = (R
1
˙q
2
1
+ R
2
˙q
2
3
)/2, respectively.

3.3 Applications 143
Lagrange’s equations for this system are
d
dt
∂T
∗
∂ ˙q
1
−
∂T
∗
∂q
1
+
∂D
∂ ˙q
1
+
∂V
∂q
1
= e
s
q
1
(a)
d
dt
∂T
∗
∂ ˙q
3
−
∂T
∗
∂q
3
+
∂D
∂ ˙q
3
+
∂V
∂q
3
= e
s
q
3
. (b)
Using the energy relationships and the generalized efforts in (a) and (b) yields
the coupled differential equations
(a) ⇒ R
1
˙q
1
−
1
C
(q
3
− q
1
− q
20
) = 0,
(b) ⇒ R
2
˙q
3
+
1
C
(q
3
− q
1
− q
20
) = v.
Example 3.18.
The circuit shown in the figure below is called a half-wave rectifier. The net-
work consists of a voltage source, v, a diode, a capacitor, C, and a resistor,
R.
3
q
q
q
+
v
+
v
d
RC
A
1
2
Kinematic analysis:
Three flow variables ( ˙q
1
, ˙q
2
, and ˙q
3
) have been assigned to the network. How-
ever, it is easy to verify that the system only has 2 degrees of freedom. Here,
we select q
1
and q
3
to be the generalized displacements, and ˙q
1
and ˙q
3
as the
corresponding generalized flows.
To eliminate the excess displacement variable, q
2
, we apply Kirchhoff’s
current law to node A. This gives ˙q
2
= ˙q
1
− ˙q
3
. Integrating this equation
leads to q
2
= q
1
− q
3
+ q
20
, where q
20
is the initial charge in the capacitor.
We therefore have an explicit expression for q
2
in terms of the generalized
displacements.
Applied effort analysis:
Here we consider the diode to be an effort regulated flow source. (See Sec-
tion 1.2.5.) In particular, the diode voltage v
d
, and the current ˙q
1
satisfy the
equation
˙q
1
= I
s
(e
αv
d
− 1), (a)

144 3 Lagrange’s Equation of Motion
where I
s
> 0, and α > 0 are constants. Using (a) it can be seen that
v
d
=
1
α
ln
˙q
1
I
s
+ 1
.
Our analysis must account for the virtual work done by the diode voltage,
v
d
.
The virtual work done by the voltage source, v, and the diode voltage v
d
is δW = (v − v
d
) δq
1
= e
s
q
1
δq
1
+ e
s
q
3
δq
3
. (Recall that the work done by a
voltage source is positive if the current flows from the negative terminal to
the positive terminal. Hence, the virtual work done by the source v is v δq
1
,
and the virtual work done by the diode voltage, v
d
, is −v
d
δq
1
). The net result
is that the generalized efforts are e
s
q
1
= v − v
d
, and e
s
q
3
= 0.
Lagrange’s equations:
The kinetic coenergy, potential energy and the dissipation function are,
T
∗
= 0, V = (q
1
− q
3
+ q
20
)
2
/(2C), and D = R ˙q
2
3
/2, respectively.
Lagrange’s equations for this system are
d
dt
∂T
∗
∂ ˙q
1
−
∂T
∗
∂q
1
+
∂D
∂ ˙q
1
+
∂V
∂q
1
= e
s
q
1
, (b)
d
dt
∂T
∗
∂ ˙q
3
−
∂T
∗
∂q
3
+
∂D
∂ ˙q
3
+
∂V
∂q
3
= e
s
q
3
. (c)
Using the energy relationships and the generalized efforts gives
(b) ⇒
1
C
(q
1
− q
3
+ q
20
) = v −
1
α
ln
˙q
1
I
s
+ 1
,
(c) ⇒ R ˙q
3
−
1
C
(q
1
− q
3
+ q
20
) = 0.
Example 3.19.
The schematic in (a) shows an electrical network that includes an opera-
tional amplifier. We would like to find a relationship between the applied
voltage, v
a
, and the voltage at terminal 3 of the operational amplifier, i.e.,
v
3
.

3.3 Applications 145
A
v
+
−
R
R
v
+
−
R
R
+
a a
3
1
2
a a
b
b
(a) (b)
i
i
i
a
1
b
v
3
Kinematic analysis:
An equivalent network model of the system is shown in (b). Here, we have
assigned the current i
a
= ˙q
a
to the branch that includes the voltage source,
v
a
, and the resistor R
a
. The current i
b
= ˙q
b
is assigned to the resistor R
b
,
and i
1
= ˙q
1
is assigned to terminal 1 of the operational amplifier.
Applying Kirchhoff’s current law to node A gives the flow constraint equa-
tion
˙q
a
+ ˙q
1
− ˙q
b
= 0.
However, the input resistance to the operational amplifier is very large and
as a result ˙q
1
≈ 0. Hence, we get ˙q
a
= ˙q
b
is the independent flow variable for
the network.
Applied effort analysis:
Using the equivalent network model we can see that the virtual work done
by the voltage source, v
a
, and the output voltage v
3
is δW = (v
a
−v
3
) δq
a
=
e
s
q
a
δq
a
. Therefore, the generalized effort is e
s
q
a
= v
a
− v
3
.
Lagrange’s equations:
The kinetic coenergy, potential energy and the dissipation function are
T
∗
= 0, V = 0, and D = (R
a
+ R
b
) ˙q
2
a
/2, respectively.
Lagrange’s equation for this system is
d
dt
∂T
∗
∂ ˙q
a
−
∂T
∗
∂q
a
+
∂D
∂ ˙q
a
+
∂V
∂q
a
= e
s
q
a
.
Which yields
(R
a
+ R
b
) ˙q
a
= v
a
− v
3
.
To eliminate ˙q
a
from the last equation we use the fact that the operational
amplifier behaves according to the rule

146 3 Lagrange’s Equation of Motion
v
3
= k
g
(v
2
− v
1
),
where k
g
is very large constant, v
1
is the voltage at terminal 1, and v
2
is the
voltage at terminal 2.
Using the equivalent network model we can see that v
1
= v
a
− R
a
˙q
a
, and
v
2
= 0. Therefore, v
3
= k
g
(R
a
˙q
a
− v
a
), from which we obtain
˙q
a
=
v
3
+ k
g
v
a
k
g
R
a
≈
v
a
R
a
.
Putting this in the equation of motion produces
(R
a
+ R
b
)
v
a
R
a
= v
a
− v
3
v
3
= −
R
b
R
a
v
a
.
We can thus conclude that the network represents an inverting amplifier with
gain R
b
/R
a
.
Example 3.20.
A model of a DC motor is shown in the figure below. The motor is excited
by a voltage source, v. The resistance and inductance of the motor coils are
modeled using R and L, respectively. The rotor has moment of inertia I, and
is subjected to torsional damping with damping coefficient b.
b
q
θ
+
v
τ
+
b
R L
I
v
DC Motor
Kinematic analysis:
The generalized displacements for the system are q, the charge in the elec-
trical circuit, and θ the angular position of the rotor. The corresponding
generalized flows are ˙q, the current in the circuit, and
˙
θ, the angular velocity
of the rotor.
Applied effort analysis:
The effort sources in this model are the applied voltage, v, the motor back
emf v
b
, and the motor torque, τ. The virtual work done by these efforts is
δW = (v −v
b
) δq + τ δθ = e
s
q
δq + e
s
θ
δθ. Therefore, the generalized efforts are
3.3 Applications 147
e
s
q
= v − v
b
, and e
s
θ
= τ. For a DC motor the back emf and the torque are
related to the generalized velocities by
v
b
= K
b
˙
θ, (a)
τ = K
t
˙q, (b)
where K
b
is the back emf constant and K
t
is the torque constant.
Lagrange’s equations:
The kinetic coenergy, potential energy and the dissipation function are
T
∗
= L ˙q
2
/2 + I
˙
θ
2
/2, V = 0, and D = R ˙q
2
/2 + b
˙
θ
2
/2, respectively.
Lagrange’s equation for this system are
d
dt
∂T
∗
∂ ˙q
−
∂T
∗
∂q
+
∂D
∂ ˙q
+
∂V
∂q
= e
s
q
, (c)
d
dt
∂T
∗
∂
˙
θ
−
∂T
∗
∂θ
+
∂D
∂
˙
θ
+
∂V
∂θ
= e
s
θ
. (d)
Using the energy relationships, the generalized efforts gives, and (a) and (b),
we get
(c) ⇒ L¨q + R ˙q = v − K
b
˙
θ,
(d) ⇒ I
¨
θ + b
˙
θ = K
t
˙q.
3.3.3 Fluid systems
A simple approach to analyzing fluid systems is to construct an equivalent
electrical circuit model for the system then, apply the electrical systems mod-
eling techniques to this equivalent circuit. In the fluid system long pipes can
be modeled as ideal inductors, valves and nozzles can be modeled as ideal
resistors, and tanks can be modeled as ideal capacitors.
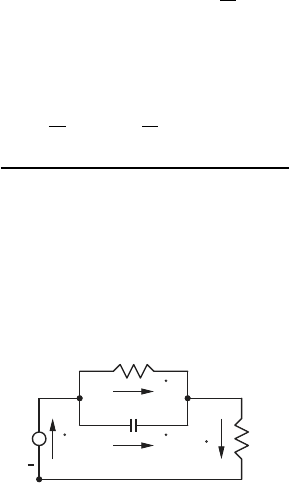
Example 3.21.
Consider the fluid system shown in Fig. 3.4a and its corresponding equiv-
alent circuit model Fig. 3.4b. In this system a pump delivers fluid to a long
pipe which is connected to a tank. The fluid exiting the tank flows through
a valve. The pump is modeled as an effort source, P , the pipe is modeled
