Fabien B. Analytical System Dynamics: Modeling and Simulation
Подождите немного. Документ загружается.

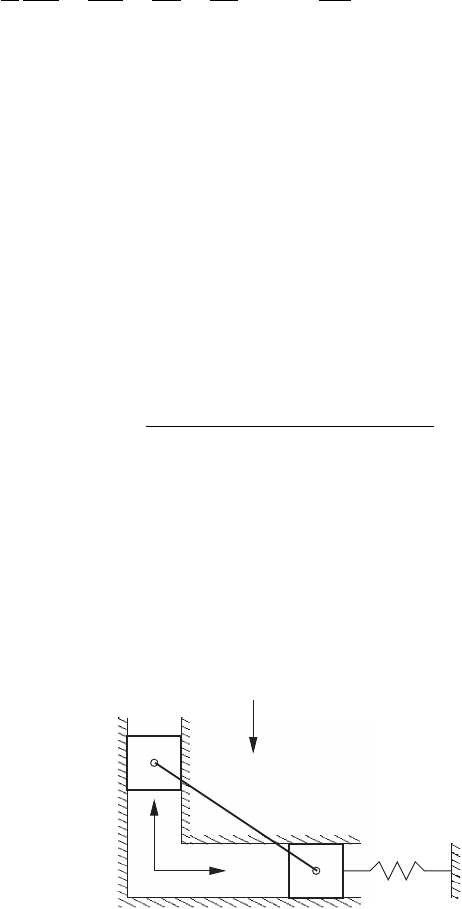
168 4 Constrained Systems
only be satisfied if the terms in the square brackets all vanish simultaneously.
Combining (a), (f) and (g) we see that the constrained dynamic system must
satisfy the differential-algebraic equations
d
dt
∂T
∗
∂f
i
−
∂T
∗
∂q
i
+
∂D
∂f
i
+
∂V
∂q
i
+
m
1
X
j=1
λ
j
∂φ
j
∂q
i
− e
s
i
= 0, i = 1, 2, ···, N,
φ
i
(q, t) = 0, i = 1, 2, ···, m
1
. (4.5)
Given a set of consistent initial conditions the N + m
1
equations in (4.5) can
be solved to determine the N + m
1
variables q and λ. In this formulation the
term λ
j
(∂φ
j
/∂q
i
) is an effort, and can be interpreted as the effort required
to ensure that the j-th constraint is satisfied.
4.2.1 Application to displacement constrained systems
This section illustrates the application of equation (4.5) to dynamic sys-
tems that contain displacement constraints. Here our goal is simply to de-
termine the equations of motion of the system, the analysis of the resultant
differential-algebraic equations is considered in Chapter 5 and Chapter 6.
Example 4.1.
The mechanism shown in the figure below consists of two sliders (A and
B) that are connected by a massless rod. The slider A has mass m
A
and
can move along the y-axis. The slider B has mass m
B
and can move along
the x-axis. A linear spring with stiffness k is attached to the slider B, and
the rod AB has length l. Note that the rod is connected to the sliders via
revolute joints at A and B. The acceleration due gravity acts downward as
shown, and the effects of friction are neglected.
A
x
y
k
g
B
An analysis of this mechanism using Lagrange’s equation proceeds as follows.

4.2 Lagrange’s Equation with Displacement Constraints 169
Kinematic analysis:
The configuration coordinates for the system are x and y which define the
positions of B and A, respectively. A mobility analysis shows that this system
has 1 degree of freedom thus, there is a constraint relationship between the
two variables x and y. In fact it is easy to see that at any instant the distance
between A and B is l, i.e., the system has the displacement constraint
φ = x
2
+ y
2
− l
2
= 0.
This constraint equation is sufficiently simple for us to eliminate one of the
two displacement variables and proceed with the analysis using a generalized
(independent) coordinate. Here however, we will retain both coordinates in
the system description.
Applied effort analysis:
The virtual work done by the weight of slider A is equal to the work done by
the applied efforts, i.e., δW = −m
A
g δy = e
s
x
δx + e
s
y
δy. Therefore, e
s
x
= 0
and e
s
y
= −m
A
g. (Note that the applied efforts do not include the efforts
due to capacitors and resistors, since those efforts are accounted for in the
potential energy and the dissipation function.)
Lagrange’s equation:
The kinetic coenergy for the system is T
∗
= (m
A
˙y
2
+ m
B
˙x
2
)/2, the po-
tential energy for the system is V = (kx
2
)/2, and the dissipation function is
D = 0.
Using equation (4.5) Lagrange’s equations of motion for this system can
be stated as
d
dt
∂T
∗
∂ ˙x
−
∂T
∗
∂x
+
∂D
∂ ˙x
+
∂V
∂x
+ λ
∂φ
∂x
= e
s
x
, (a)
d
dt
∂T
∗
∂ ˙y
−
∂T
∗
∂y
+
∂D
∂ ˙y
+
∂V
∂y
+ λ
∂φ
∂y
= e
s
y
, (b)
φ(x, y) = 0. (c)
Using T
∗
, V , D and φ, given above, equations (a), (b) and (c) become
(a) ⇒ m
B
¨x + kx + 2λx = 0,
(b) ⇒ m
A
¨y + 2λy = −m
A
g,
(c) ⇒ x
2
+ y
2
− l
2
= 0.
These are a set of differential-algebraic equations that determine the behavior
of the system. There are two differential equations, (a) and (b), and one

170 4 Constrained Systems
algebraic equation, (c), that are used to determine the displacements x and
y, and the Lagrange multiplier λ. Given a consistent set of initial conditions
we can solve these differential-algebraic equations to determine the trajectory
of the system. Numerical techniques for the solution of these differential-
algebraic equations will be discussed in Chapter 5 and Chapter 6.
Example 4.2.
The figure below shows a planar slider crank mechanism. The crank AB
has mass m
1
and moment of inertia I
1
about the center of mass. The length
of the crank is l
1
, and the center of mass is at distance l
1
/2 from A. The
connecting rod BC has mass m
2
and moment of inertia I
2
about the center
of mass. The length of the connecting rod is l
2
, and the center of mass is a
distance l
2
/2 from B. The slider D has mass m
3
. A torque, τ, is applied to
the crank. An analysis of this device proceeds as follows.
τ
θ
2
m , I
2
2
m , I
1
1
y
x
D
C
B
m
3
A
θ
1
Kinematic analysis:
Let, (x
1
, y
1
) denote the coordinates is the center of mass of the crank AB,
with respect to the fixed rectangular coordinate system x-y. Similarly, let
(x
2
, y
2
) be the coordinate of the center of mass of the connecting rod BC,
and let x
3
be the coordinate of the slider D. The angle θ
1
gives the orientation
of the crank with respect to the x-axis, and the angle θ
2
gives the orientation
of the connecting rod with respect to the x-axis. Thus, the 7 configuration
displacement variables for the system are x
1
, y
1
, θ
1
, x
2
, y
2
, θ
2
, and x
3
.
A mobility analysis of the system shows that there is 1 degree of free-
dom hence, there are 6 constraint equations that relate the 7 configuration
displacements described above. These constraints are determined as follows.
The mass centers of the crank and connecting rod are determined via the
4 displacement constraints

4.2 Lagrange’s Equation with Displacement Constraints 171
φ
1
= x
1
−
l
1
2
cos θ
1
= 0,
φ
2
= y
1
−
l
1
2
sin θ
1
= 0,
φ
3
= x
2
− (l
1
cos θ
1
+
l
2
2
cos θ
2
) = 0,
φ
4
= y
2
− (l
1
sin θ
1
+
l
2
2
sin θ
2
) = 0.
The vector loop closure equation
¯
AB +
¯
BC =
¯
AC yields the 2 constraints
φ
5
= l
1
cos θ
1
+ l
2
cos θ
2
− x
3
= 0,
φ
6
= l
1
sin θ
1
+ l
2
sin θ
2
= 0.
These 6 displacement constraints could be used to eliminate 6 of the config-
uration variables from the problem description. Here however, all 7 displace-
ment variables are retained in the problem formulation.
Applied effort analysis:
The virtual work done by the applied torque, τ, is equal to the work done by
the applied efforts, i.e., δW = τ δθ
1
= e
s
x
1
δx
1
+ e
s
y
1
δy
1
+ e
s
θ
1
δθ
1
+ e
s
x
2
δx
2
+
e
s
y
2
δy
2
+ e
s
θ
2
δθ
2
+ e
s
x
3
δx
3
. Therefore, all the configuration efforts are zero
except e
s
θ
1
= τ.
Lagrange’s equations:
The kinetic coenergy of the system is
T
∗
=
1
2
m
1
( ˙x
2
1
+ ˙y
2
1
) +
1
2
I
1
˙
θ
2
1
+
1
2
m
2
( ˙x
2
2
+ ˙y
2
2
) +
1
2
I
2
˙
θ
2
2
+
1
2
m
3
˙x
2
3
,
the potential energy is V = 0, and the dissipation function is D = 0. To
simplify the enumeration of the equations of motion let us define the dis-
placement vector q as q = [x
1
, y
1
, θ
1
, x
2
, y
2
, θ
2
, x
3
]
T
, and the corresponding
flow vector f as f = [ ˙x
1
, ˙y
1
,
˙
θ
1
, ˙x
2
, ˙y
2
,
˙
θ
2
, ˙x
3
]
T
. Then equation (4.5) gives

172 4 Constrained Systems
m
1
¨x
1
+ λ
1
= 0,
m
1
¨y
1
+ λ
2
= 0,
I
1
¨
θ
1
+ λ
1
l
1
2
sin θ
1
− λ
2
l
1
2
cos θ
1
+ λ
3
l
1
sin θ
1
−λ
4
l
1
cos θ
1
− λ
5
l
1
sin θ
1
+ λ
6
l
1
cos θ
1
= τ,
m
2
¨x
2
+ λ
3
= 0,
m
2
¨y
2
+ λ
4
= 0,
I
2
¨
θ
2
+ λ
3
l
2
2
sin θ
2
− λ
4
l
2
2
cos θ
2
−λ
5
l
2
sin θ
2
+ λ
6
l
2
cos θ
2
= 0,
m
3
¨x
3
− λ
5
= 0,
x
1
−
l
1
2
cos θ
1
= 0,
y
1
−
l
1
2
sin θ
1
= 0,
x
2
− (l
1
cos θ
1
+
l
2
2
cos θ
2
) = 0,
y
2
− (l
1
sin θ
1
+
l
2
2
sin θ
2
) = 0,
l
1
cos θ
1
+ l
2
cos θ
2
− x
3
= 0,
l
1
sin θ
1
+ l
2
sin θ
2
= 0.
Given a consistent set of initial conditions these differential-algebraic equa-
tions can be solved to determine the trajectory of the slider-crank mechanism.
Example 4.3.
The figure below shows a planar fourbar mechanism. The crank AB has
mass m
1
and moment of inertia I
1
about the center of mass. The length
of the crank is l
1
, and the center of mass is at distance l
1
/2 from A. The
connecting rod BC has mass m
2
and moment of inertia I
2
about the center
of mass. The length of the connecting rod is l
2
, and the center of mass is a
distance l
2
/2 from B. The follower DC has mass m
3
and moment of inertia
I
3
about the center of mass. The length of the follower is l
3
and the center
of mass is at distance l
3
/2 from D. The distance from A to D is l
4
, and a
torque τ is applied to the crank AB. The equations of motion for this system
can be determined as follows.
θ
y
θ
3
x
2
θ
D
C
B
m
3
, I
3
m
2
, I
2
m
1
, I
1
A
τ
1

4.2 Lagrange’s Equation with Displacement Constraints 173
Kinematic analysis:
The angle θ
1
gives the orientation of the crank with respect to the x-axis, Let
(x
2
, y
2
) be the coordinate of the center of mass of the connecting rod BC, and
let θ
2
be the angle between the x-axis and the connecting rod. Finally, the
angle θ
3
gives the orientation of the follower DC with respect to the x-axis.
Thus, the configuration displacement variables for the system are, θ
1
, x
2
, y
2
,
θ
3
, and θ
3
.
A mobility analysis of the system shows that there is n = 1 degree of
freedom. Typically, the angle θ
1
is selected as the independent displacement.
Here, however, we have chosen N = 5 configuration displacements to de-
scribe the system. Therefore, we must determine m
1
= N −n = 4 constraint
equations that relate these configuration displacements.
Two of the constraints provide the coordinates of the center of mass of the
connecting rod, i.e.,
φ
1
= x
2
− (l
1
cos θ
1
+
l
2
2
cos θ
2
) = 0,
φ
2
= y
2
− (l
1
sin θ
1
+
l
2
2
sin θ
2
) = 0.
The vector loop closure equation
¯
AB +
¯
BC =
¯
AD +
¯
DC yields the other two
constraints, i.e.,
φ
3
= l
1
cos θ
1
+ l
2
cos θ
2
− l
3
cos θ
3
− l
4
= 0,
φ
4
= l
1
sin θ
1
+ l
2
sin θ
2
− l
3
sin θ
3
= 0.
From the constraints φ
1
and φ
2
it can be seen that the variables x
2
and y
2
can be easily eliminated from the problem description. However, the deter-
mination of θ
2
and θ
3
from φ
3
and φ
4
is non-trivial. Here, we choose to keep
all the configuration coordinates in the system description.
Applied effort analysis:
The virtual work done by the applied torque, τ, is equal to the work done by
the applied efforts, i.e., δW = τ δθ
1
= e
s
θ
1
δθ
1
. Therefore, all the configuration
efforts are zero except e
s
θ
1
= τ.
Lagrange’s equations:
The kinetic coenergy of the system is
T
∗
=
1
2
(I
1
+ m
1
l
2
1
/4)
˙
θ
2
1
+
1
2
m
2
( ˙x
2
2
+ ˙y
2
2
) +
1
2
I
2
˙
θ
2
2
+
1
2
(I
3
+ m
3
l
2
3
/4)
˙
θ
2
3
,
the potential energy is V = 0, and the dissipation function is D = 0.
To apply equation (4.5) directly, define the displacement vector q as q =

174 4 Constrained Systems
[θ
1
, x
2
, y
2
, θ
2
, θ
3
]
T
, and the flow vector f as f = [
˙
θ
1
, ˙x
2
, ˙y
2
,
˙
θ
2
,
˙
θ
3
]
T
. Then
equation (4.5) gives
(I
1
+ m
1
l
2
1
/4)
¨
θ
1
+ λ
1
l
1
sin θ
1
− λ
2
l
1
cos θ
1
− λ
3
l
1
sin θ
1
+ λ
4
l
1
cos θ
1
= τ,
m
2
¨x
2
+ λ
1
= 0,
m
2
¨y
2
+ λ
2
= 0,
I
2
¨
θ
2
+ λ
1
l
2
2
sin θ
2
− λ
2
l
2
2
cos θ
2
− λ
3
l
2
sin θ
2
+ λ
4
l
2
cos θ
2
= 0,
(I
3
+ m
3
l
2
3
/4)
¨
θ
3
+ λ
3
l
3
sin θ
3
− λ
4
l
3
cos θ
3
= 0,
x
2
− (l
1
cos θ
1
+
l
2
2
cos θ
2
) = 0,
y
2
− (l
1
sin θ
1
+
l
2
2
sin θ
2
) = 0,
l
1
cos θ
1
+ l
2
cos θ
2
− l
3
cos θ
3
− l
4
= 0,
l
1
sin θ
1
+ l
2
sin θ
2
− l
3
sin θ
3
= 0.
These 9 differential-algebraic equations can be solved to determine the tra-
jectory of the system.
4.3 Lagrange’s Equation with Flow Constraints
We now turn our attention to dynamic systems that include flow constraints
in the Pfaffian form
ψ
j
(q, f, t) =
N
X
i=1
a
ji
(q, t) f
i
+ a
j
(q, t) = 0, j = 1, 2, ···, m
2
, (a)
where q=[q
1
, q
2
, ···, q
N
]
T
are the displacements, and f=[f
1
, f
2
, ···, f
N
]
T
are
the flows. Also, the coefficients a
ji
and a
j
are functions of the displacements,
q, and the time, t. It is assumed that the m
2
constraints are independent.
In particular, let a
ji
be the (j, i)-th element of the m
2
× N matrix A, i.e.,
A=[a
ji
]. Then, it is assumed the matrix A has rank m
2
along the solution
trajectory. It is further assumed that the configuration variables are arranged
such that the first m
2
columns of A are linearly independent. (Note that
this rearrangement of variables is only required to simplify the derivation
presented in this section. In the application of the theory we are not required
to perform this manipulation of the system variables.)
If the constraints are holonomic then equation (a) can be integrated to
find a displacement constraint of the form (4.2), and the results of Section
4.2 can be applied. If the constraints are nonholonomic, or we choose not to
integrate the flow constraints to obtain displacement constraints then, the
analysis of the system proceeds as follows.

4.3 Lagrange’s Equation with Flow Constraints 175
As in the previous section (and Section 3.2) it can be shown that the
variational form of the first law of thermodynamics leads to
N
X
i=1
d
dt
∂T
∗
∂f
i
−
∂T
∗
∂q
i
+
∂D
∂f
i
+
∂V
∂q
i
− e
s
i
δq
i
= 0, (b)
where T
∗
is the kinetic coenergy, V is the potential energy, D is the dissipation
function, and e
s
i
is the applied effort associated with the i-th configuration
displacement. Due to the flow constraints, (a), the virtual displacements δq
i
are related via the m
2
independent equations
N
X
i=1
a
ji
(q, t) δq
i
= 0, j = 1, 2, ···, m
2
. (c)
Equation (c) is obtained by considering a variation of the flow constraints
(a), and can be written in matrix form as
A δq = [A
D
A
I
]
δq
D
δq
I
= A
D
δq
D
+ A
I
δq
I
= 0,
where A
D
contains the first m
2
columns of A, q
D
= [q
1
, q
2
, ···, q
m
2
]
T
, and
q
I
= [q
m
2
+1
, q
m
2
+2
, ···, q
N
]
T
. We have arranged the variables so that A
D
is
nonsingular hence,
δq
D
= −A
−1
D
A
I
δq
I
.
This last equation indicates the virtual displacements δq
D
are dependent on
the virtual displacements δq
I
.
To account for the constraints (c) in equation (b) we will employ the
method of Lagrange multipliers. That is, multiply the j-th equation in (c) by
µ
j
and add the result to equation (b) to get
N
X
i=1
d
dt
∂T
∗
∂f
i
−
∂T
∗
∂q
i
+
∂D
∂f
i
+
∂V
∂q
i
− e
s
i
+
m
2
X
j=1
µ
j
a
ji
δq
i
= 0. (d)
Here, µ
j
are functions of the time, and are called the Lagrange multipliers.
We will select these m
2
multipliers so that
d
dt
∂T
∗
∂f
i
−
∂T
∗
∂q
i
+
∂D
∂f
i
+
∂V
∂q
i
− e
s
i
+
m
2
X
j=1
µ
j
a
ji
= 0, i = 1, 2, ···, m
2
. (e)
Thus, we have used the Lagrange multipliers to eliminate the first m
2
terms
of the summation in equation (d). As a result equation (d) becomes

176 4 Constrained Systems
N
X
i=1+m
2
d
dt
∂T
∗
∂f
i
−
∂T
∗
∂q
i
+
∂D
∂f
i
+
∂V
∂q
i
− e
s
i
+
m
2
X
j=1
µ
j
a
ji
δq
i
= 0. (f )
By construction the N − m
2
virtual displacements, δq
i
, i = m
2
+ 1, ···, N,
can all be chosen independently. Since the virtual displacements in (f) can
be varied arbitrarily, this equation will be satisfied only if
d
dt
∂T
∗
∂f
i
−
∂T
∗
∂q
i
+
∂D
∂f
i
+
∂V
∂q
i
−e
s
i
+
m
2
X
j=1
µ
j
a
ji
= 0, i = m
2
+ 1, m
2
+ 2, ···, N.
(g)
Combining equations (e), (g) and (a) we see that the trajectory of the
constrained dynamic system satisfies
d
dt
∂T
∗
∂f
i
−
∂T
∗
∂q
i
+
∂D
∂f
i
+
∂V
∂q
i
+
m
2
X
j=1
µ
j
a
ji
− e
s
i
= 0, i = 1, 2, ···, N,
N
X
i=1
a
ji
(q, t) f
i
+ a
j
(q, t) = 0, j = 1, 2, ···, m
2
. (4.6)
Given a set of initial conditions, that are consistent with the constraints,
these N + m
2
differential-algebraic equations can be integrated to determine
the N displacements, q, and the m
2
Lagrange multiplier, µ.
Note that holonomic flow constraints can be treated directly using equa-
tion (4.6), or they can be integrated to obtain displacement constraints which
are then used in equation (4.5). On the other hand, the derivatives of the dis-
placement constraints (4.2) are in the Pfaffian form, in fact, a
ji
= ∂φ
j
/∂q
i
and a
j
= ∂φ
j
/∂t. Therefore, equation (4.6) can be used to analyze systems
with displacement constraints. However, converting the displacement con-
straints to flow constraints must be used with some care, since there is no
assurance that the original displacement constraints will be satisfied exactly.
This issue is considered in more detail in Chapter 5.
4.3.1 Application to flow constrained systems
This section presents some examples that illustrate the application of equa-
tion (4.6) to the modeling of dynamic systems that have flows constraints
which can be written in the Pfaffian form. The first example has integrable
flow constraints, and the other examples all have nonholonomic constraints.

4.3 Lagrange’s Equation with Flow Constraints 177
Example 4.4.
The network shown in the figure below can be analyzed using equation (4.6)
as follows.
v(t)
q
1
q
2
q
3
q
4
q
5
R
1
L
1
L
2
C
1
C
2
q
6
+
A B C
D
Kinematic analysis:
Six configuration flows are assigned to the model, i.e., ˙q
1
, ˙q
2
, ···, ˙q
6
. These
variables are not all independent, in fact there are n = B−N +1 = 6−4+1 = 3
independent flow variables. (Recall that, B is the number of branches, and
N is the number of nodes in the network.) This implies that there are three
independent constraint equations that relate the 6 flow variables. These con-
straints can be found by applying Kirchhoff’s current law to the nodes A, B
and C of thew network. Doing so gives the 3 flow constraints
ψ
1
= ˙q
1
− ˙q
2
= 0,
ψ
2
= ˙q
2
+ ˙q
3
− ˙q
4
= 0,
ψ
3
= ˙q
4
+ ˙q
5
+ ˙q
6
= 0.
Clearly these constraints are integrable and we can use them to (i) obtain
displacement constraints of the form (4.2), and/or (ii) eliminate three of the
flow variables for the problem description. Here however, we will retain all
the variables in the problem description.
Applied effort analysis:
The virtual work done by the applied voltage v(t) is δW = v(t) δq
1
. Thus,
the applied efforts e
s
q
i
are all zero except e
s
q
1
= v(t).
Lagrange’s equations:
The kinetic coenergy for the system is
T
∗
=
1
2
(L
1
˙q
2
2
+ L
2
˙q
2
4
),
the potential energy is
V =
q
2
3
2C
1
+
q
2
5
2C
2
,
and the dissipation function is
