Fabien B. Analytical System Dynamics: Modeling and Simulation

Подождите немного. Документ загружается.

178 4 Constrained Systems

D =

˙q

In terms of the Pfaﬃan form, (4.1), the constraints ψ

, ψ

and ψ

have the

coeﬃcients

A = [a

] =





1 −1 0 0 0 0

0 1 1 −1 0 0

0 0 0 1 1 1





and a

= 0, j = 1, 2, ···, 6. Hence, Lagrange’s equations of motion, (4.6), are

= v(t),

¨q

− µ

+ µ

= 0,

+ µ

= 0,

¨q

− µ

+ µ

= 0,

+ µ

= 0,

˙q

+ µ

= 0,

˙q

− ˙q

= 0,

˙q

+ ˙q

− ˙q

= 0,

˙q

+ ˙q

= 0.

To solve these diﬀerential-algebraic equations we require a set of initial condi-

tions that are consistent with the constraints ψ

, ψ

and ψ

. These equations

of motion are relatively simple and it is not diﬃcult to reduce these to three

ordinary diﬀerential equations involving three independent ﬂow variables (see

Problem 6).

Example 4.5.

The ﬁgure below shows a ﬁxed rectangular coordinate system x-y-z. The

x-axis make an angle α with respect to the horizontal. A thin disk with

radius r rolls without slipping on the inclined x-y plane. The origin of the

-y

-z

rectangular coordinate system is located at the geometric center of

the disk. Also, the x

-axis and z

-axis are in the radial direction of the disk.

The disk has a mass m, a moment of inertia I

about the y

-axis, and a

moment of inertia I

about the x

-axis and the z

-axis. The acceleration due

to gravity, g, acts downward as shown, i.e., perpendicular to the horizontal

and at angle α with respect to the z-axis.

4.3 Lagrange’s Equation with Flow Constraints 179

Kinematic analysis:

The coordinate of the center of mass of the disk, with respect to the x-y-

z coordinate system, is deﬁned by x, y. (The z coordinate of the center of

mass is r at all times.) The orientation of the disk is deﬁned by the angles θ

and φ. Since the disk is rolling without slipping the velocity of the center of

mass must satisfy the nonholonomic constraints

= ˙x − r

φ cos θ = 0,

= ˙y − r

φ sin θ = 0.

(a)

These two equations can not be integrated to eliminate the x and y displace-

ments from the system description. Hence, all four displacements (x, y, θ and

φ) are retained in the model.

Applied eﬀort analysis:

The weight of the disk is given by the vector ¯w = mg(−sin α

i − cos α

k),

where

i is the unit vector along the x-axis, and

k is the unit vector along the

z-axis. Since the force along the z-axis does no virtual work, the virtual work

done by the weight is δW = −mg sin α δx. Therefore, the applied eﬀorts are

all zero except e

= −mg sin α.

Lagrange’s equations:

The kinetic coenergy for the system is

∗

m( ˙x

+ ˙y

) +

+ mr

)

The potential energy is V = 0, and the dissipation function is D = 0. To use

equation (4.6) let q = [x, y, φ, θ]

. Also, using the notation of equation (4.1)

to describe the constraints (a) implies that

= 1, a

= 0, a

= −r cos θ, a

= 0, a

= 0,

= 0, a

= 1, a

= −r sin θ, a

= 0, a

= 0.

180 4 Constrained Systems

Putting these in equation (4.6) gives

− mg sin α = 0,

= 0,

+ mr

)

φ − µ

r cos θ − µ

r sin θ = 0,

θ = 0,

˙x −r

φ cos θ = 0,

˙y − r

φ sin θ = 0.

These diﬀerential-algebraic equations can be reduced to the diﬀerential equa-

tions

+ mr

)

φ + mgr sin α cos(θ

+ ωt) = 0,

˙x −r

φ cos(θ

+ ωt) = 0,

˙y − r

φ sin(θ

+ ωt) = 0.

To obtain this result we have used the fact that θ = θ

+ ωt, where θ

and

ω are constants, and t is the time. These diﬀerential equations can easily be

solved given initial conditions for x, y and φ.

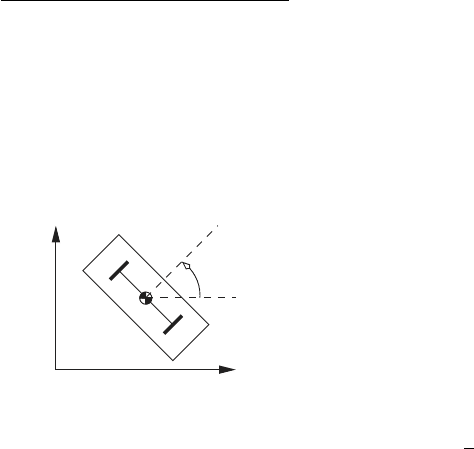
Example 4.6.

The ﬁgure below shows a two-wheeled vehicle that moves in the x-y plane.

The wheels at A and B roll without slipping in the plane. Both wheels have

the same diameter and are connected by an axle through their centers. The

vehicle has mass m, and moment of inertia I about the center of mass in the

z direction.

Kinematic analysis:

The coordinate of the center of mass of the vehicle is x, y. The angle θ +

gives the orientation the axle with respect to the x-axis. Since the wheels roll

without slipping the x and y velocities of the center of mass must satisfy the

nonholonomic constraint

= ˙y − ˙x tan θ = ˙y cos θ − ˙x sin θ = 0. (a)

4.3 Lagrange’s Equation with Flow Constraints 181

This constraint indicates the the velocity of the vehicle is normal to the axle

at all times.

Applied eﬀort analysis:

There are no applied eﬀorts for this problem.

Lagrange’s equations:

The kinetic coenergy of the systems is

∗

m( ˙x

+ ˙y

) +

the potential energy is V = 0, and the dissipation function is D = 0. To

apply equation (4.6) deﬁne the displacement vector q = [x, y, θ]

. Also, note

that the coeﬃcients of the ﬂow constraint (a) in the Pfaﬃan form (4.1) are

= −sin θ, a

= cos θ, a

= 0, a

= 0.

Using these terms the equations of motion can be written as

m¨x −µ

sin θ = 0,

m¨y + µ

cos θ = 0,

θ = 0,

˙y cos θ − ˙x sin θ = 0.

Given a set of initial conditions these 4 diﬀerential-algebraic equations can

be solved to determine x, y, θ and µ

Example 4.7.

The ﬁgure below shows a three-wheeled vehicle that moves in the x-y plane.

The wheels at A, B and C roll without slipping, and the vehicle has mass m,

and moment of inertia I about the center of mass in the z direction.

182 4 Constrained Systems

Kinematic analysis:

The coordinates of the center of mass of the vehicle are x, y, and the ori-

entation of the vehicle with respect to the x-axis is given by the angle θ.

The angle φ measures the orientation of the steering wheel at C relative to

the body of the vehicle. Since the wheels A and B roll without slipping the

velocity of the center of mass satisﬁes the nonholonomic constraint

= ˙y − ˙x tan θ = ˙y cos θ − ˙x sin θ = 0. (a)

This constraint indicates that the velocity of the center of mass is directed

along the line OC at all times. Also, since the wheel at C rolls without slip-

ping the components of the velocity of the point C satisfy the nonholonomic

constraint

= tan(θ + φ), (b)

where v

is the x component of the velocity at C, and v

is the y component

of the velocity at C. From the ﬁgure above it can be seen that

(x + l cos θ) = ˙x −l

θ sin θ,

(y + l sin θ) = ˙y + l

θ cos θ.

Using these in equation (b) gives the constraint

= ˙y cos(θ + φ) − ˙x sin(θ + φ) + l

θ cos φ = 0. (c)

Applied eﬀort analysis:

There are no applied eﬀorts for this problem.

Lagrange’s equations:

4.4 Lagrange’s Equation with Eﬀort Constraints and Dynamic Constraints 183

The kinetic coenergy of the system is

∗

m( ˙x

+ ˙y

) +

the potential energy is V = 0, and the dissipation function is D = 0. If we

deﬁne the displacement vector q as q = [x, y, θ]

then, the coeﬃcients of the

ﬂow constrains (a) and (c) can be given in the Pfaﬃan form (4.1) as

= −sin θ, a

= cos θ, a

= 0, a

= 0,

= −sin(θ + φ), a

= cos(θ + φ), a

= l cos φ, a

= 0,

Note that the steering angle, φ, is treated as a ‘control’ input to the system.

With these deﬁnitions the equations of motion (4.6) can be written as

m¨x −µ

sin θ − µ

sin(θ + φ) = 0,

m¨y + µ

cos θ + µ

cos(θ + φ) = 0,

θ + µ

l cos φ = 0,

˙y cos θ − ˙x sin θ = 0,

˙y cos(θ + φ) − ˙x sin(θ + φ) + l

θ cos φ = 0.

These 5 diﬀerential-algebraic equations can be integrated to ﬁnd the tra-

jectory of the system given initial conditions, that are consistent with the

constraints, and a steering angle φ.

4.4 Lagrange’s Equation with Eﬀort Constraints and

Dynamic Constraints

In this text we use dynamic constraint equations and eﬀort constraint equa-

tions to account for regulated eﬀort/ﬂow sources in the systems model. Some

system elements that can be modeled as regulated sources include, DC mo-

tors, diodes, transistors, operational ampliﬁers and Coulomb friction. Also,

dynamic control system elements can easily be accommodated using this ap-

proach.

The dynamic constraints are in the form of diﬀerential equations as de-

scribed by equation (4.3), and the eﬀort constraints are algebraic equations

as described by equation (4.4). If the system contains regulated sources that

are described using these constraint equations then we can simply append

the dynamic constraints and eﬀort constraints to the Lagrange’s equation

(4.5), or (4.6). Note however, that the eﬀorts in the dynamic constraints, and

184 4 Constrained Systems

the eﬀorts in the eﬀort constraints must be accounted for in the virtual work

expression.

The examples below illustrate how dynamic constraints and eﬀort con-

straints can be included in the systems model.

Example 4.8.

A simple model of a full-wave rectiﬁer is shown in the ﬁgure below. The net-

work shows two diodes connected to voltage sources v

(t) and v

(t). These

voltages are the output from a center tapped transformer, and are such that

(t) is 180

◦

out of phase with v

(t). The circuit also includes a capacitor,

C, and a load resistor R.

v (t)

Kinematic analysis:

We have assigned ﬂow coordinates ˙q

, ˙q

and ˙q

to the model. These ﬂows

are not all independent since, at node A, Kirchhoﬀ’s current law requires

= ˙q

+ ˙q

− ( ˙q

+ ˙q

) = 0.

Applied eﬀort analysis:

The voltage sources behave according to the equations v

(t) = V sin ωt and

(t) = V sin(ωt+π) where V and ω are constants. The diodes in the network

satisfy the eﬀort constraints

= ˙q

− I

(exp

αv

−1) = 0,

= ˙q

− I

(exp

αv

−1) = 0,

where I

> 0 and α > 0 are constant and depend on the particular diode

employed. In these equations v

is the voltage across the diode at the top

of the network, and v

is the voltage across the diode at the bottom of the

network.

The virtual work of all the applied voltages is thus,

4.4 Lagrange’s Equation with Eﬀort Constraints and Dynamic Constraints 185

δW = (v

− v

) δq

+ (v

− v

) δq

= e

δq

+ e

δq

Lagrange’s equations:

The kinetic coenergy for the system is T

∗

= 0, the potential energy is

V = q

/(2C), and the dissipation function is D = R ˙q

/2. Using these terms

it can be seen that the equations of motion for the system are

= v

− v

= v

− v

− µ

= 0,

R ˙q

− µ

= 0,

˙q

+ ˙q

− ( ˙q

+ ˙q

) = 0,

˙q

− I

(exp

αv

−1) = 0,

˙q

− I

(exp

αv

−1) = 0.

The ﬁrst 5 equations are due to (4.6), and the last 2 equations are the eﬀort

constraints Γ

and Γ

. These 7 diﬀerential-algebraic equations can be solved

to determine the variables q

, q

, µ

, v

, and v

Example 4.9.

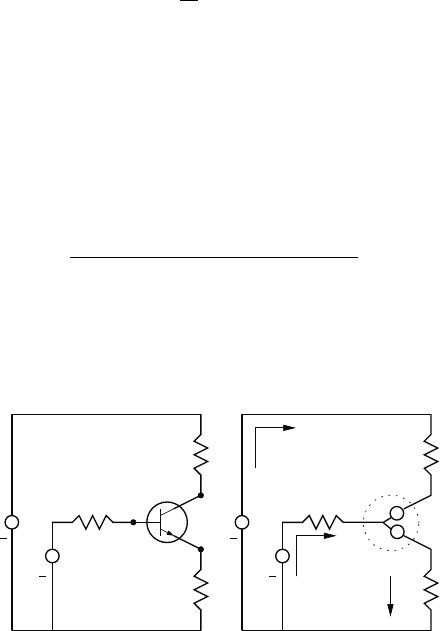
An electrical network with an NPN bipolar junction transistor is shown in

the ﬁgure (a) below. We would like to ﬁnd the equations that describe the

behavior of this system.

(a)

(b)

Kinematic analysis:

As described in Chapter 1 we will treat the transistor as voltage regulated

current source. In particular, the currents at the base (B), collector (C) and

emitter (E) are determined by the voltages at these nodes. An equivalent

186 4 Constrained Systems

circuit model for the transistor is shown in the ﬁgure (b). In this equiva-

lent network model v

and v

denote the base-emitter and base-collector

voltages, respectively. Also, we have assigned the ﬂow variables (i.e., the cur-

rents) i

= ˙q

, i

= ˙q

and i

= ˙q

to the branches of the network. We note

that this circuit has two independent loops hence, only two of the assigned

currents can be treated as independent variables. By summing the ﬂows into

the transistor we get the ﬂow constraint equations

ψ = i

+ i

− i

= 0.

Applied eﬀort analysis:

Using the Ebers-Moll model for the transistor the voltages v

, v

, and

currents i

, i

must satisfy the eﬀort constraint equations









−



−I



αv

− 1

αv

− 1







where the nonnegative parameters I

, I

, and α are properties of the

transistor.

The virtual work done by the eﬀorts in the equivalent circuit is

δW = (v

+ v

) δq

+ v

δq

− v

δq

Lagrange’s equations:

The kinetic coenergy, potential energy and dissipation function for the circuit

are, T

∗

= 0, V = 0, and

D =

˙q

+ R

˙q

+ R

˙q

respectively. Hence, Lagrange’s equations of motion (3.9) yields

˙q

+ µ = v

+ v

˙q

+ µ = v

˙q

− µ = −v

Given a set of consistent initial conditions, these three diﬀerential equations

along with the eﬀort constraints Γ

= 0, and Γ

= 0, and the ﬂow constraint

ψ = 0, can be solved to determine the six variables q

(t), q

(t), v

(t),

(t), and µ(t).

4.4 Lagrange’s Equation with Eﬀort Constraints and Dynamic Constraints 187

Example 4.10.

This example develops the equations of motion for a DC motor system with

proportional plus integral (PI) position control. The motor model includes

the inductance of the coil L, and the resistance of the coil, R. The rotor has

moment of inertia I, and is subject to torsional damping which is modeled

as a linear torsional damper with damping coeﬃcient b. In this system the

angular displacement of the motor is required to follow a desired trajectory

(t). To accomplish this the input voltage for the motor is determined from

a PI feedback control law.

R L

DC Motor

Kinematic analysis:

The generalized ﬂow variables for the model are the motor current, ˙q, and

the shaft speed,

θ.

Applied eﬀort analysis:

The eﬀorts associated with this model are (i) the back emf voltage, v

, (ii)

the motor torque, τ, and (iii) the input voltage, v(t). The back emf and the

motor torque are determined by the eﬀort constraint equations

= v

− K

θ = 0,

= τ − K

˙q = 0,

where K

is the back emf constant, and K

is the torque constant for the

motor.

The voltage input for the motor is determined from the control law

v(t) = K

(θ − θ

) + K

(θ − θ

) dt. (a)

In this equation K

is the proportional controller gain, and K

is the integral

controller gain. The ﬁrst term in equation (a) produces an input voltage that

is proportional to the error between the motor angle, θ, and the desired angle

. The second term in equation (a) produces a voltage that is proportional

to the integral of the error between the motor angle and the desired angle. If

we introduce the dynamic variable s so that

= θ − θ