Fabien B. Analytical System Dynamics: Modeling and Simulation

Подождите немного. Документ загружается.

148 3 Lagrange’s Equation of Motion

as ﬂuid inertia, L

, the tank is modeled as a ﬂuid capacitance, C

, and the

valve is modeled as a ﬂuid resistance, R

Kinematic analysis:

As shown in Fig. 3.4b a ﬂow variable is assigned to each element of the

system. However, there are only two independent variables (n = B −N + 1 =

4 − 3 + 1 = 2.) Here, we select Q

and Q

as the generalized ﬂows.

To eliminate the ﬂows Q

and Q

we note that the continuity of ﬂow at

nodes A and B gives, Q

= Q

, and Q

= Q

− Q

, respectively. Integrating

these equations leads to

= V

+ V

, (a)

= V

− V

+ V

. (b)

Here, V

is the volume (displacement) that corresponds to the ﬂow Q

, for

i = 1, 2, 3, 4. (Note that Q

.) Also, V

and V

represent initial volumes.

Applied eﬀort analysis:

The virtual work done by the pressure source, P , is δW = P δV

. However,

from (a) we get that δV

= δV

. Hence, δW = P δV

= e

δV

+ e

δV

Therefore, the generalized eﬀorts are e

= P , and e

= 0.

Lagrange’s equations:

The kinetic coenergy, potential energy and the dissipation function are

∗

= L

/2, V = (V

− V

+ V

)

/(2C

), and D = R

/2, respectively.

Lagrange’s equations for this system are

∂T

∗

∂

−

∂T

∗

∂V

∂D

∂

∂V

= e

, (c)

∂T

∗

∂

−

∂T

∗

∂V

∂D

∂

∂V

= e

. (d)

Using the energy relationships and the generalized eﬀorts gives

− V

+ V

) = P, (e)

(d) ⇒ R

−

− V

+ V

) = 0. (f)

Equations (e) and (f) can be written in terms of the generalized ﬂows instead

of the generalized displacements. Speciﬁcally, put (f) into (e), and diﬀeren-

tiate (f) to get

3.3 Applications 149

(e) ⇒ L

+ R

= P,

(f) ⇒ R

−

− Q

) = 0.

Example 3.22.

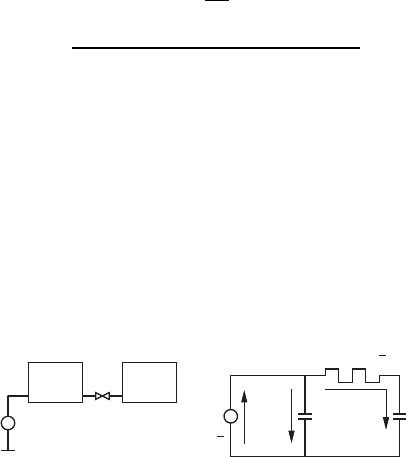
Figure (a) below shows a schematic of a ﬂuid system, and the Fig. (b) shows

the equivalent network model for the system. The pump supplies ﬂuid to the

ﬁrst tank with given pressure, P . The tanks are connected to each other via

a nonlinear valve. Each tank is treated as an ideal capacitor with capacitance

and C

. The pressure drop across the nonlinear valve, P

, satisﬁes the

equation,

= R

, (a)

where R

is a constant and

is the volume ﬂow rate through the valve.

(a) (b)

Pump

Nonlinear

valve

Tank

C C

Kinematic analysis:

Three ﬂow variables have been assigned to the system, however there are

only two independent variables (n = B − N + 1 = 3 − 2 + 1 = 2.) Here, we

select Q

and Q

as the generalized ﬂows. The continuity of ﬂow at the tank

gives Q

= Q

− Q

. Integrating this equation leads to

= V

− V

+ V

. (b)

Here, V

is the volume (displacement) that corresponds to the ﬂow Q

, for

i = 1, 2, 3. (Note that Q

.) Also, V

represents the initial volume in the

tank C

Applied eﬀort analysis:

The virtual work done by the pressure source, P , and by the nonlinear valve

is δW = P δV

−P

δV

= e

δV

. Therefore, the generalized eﬀorts

are e

= P , and e

= −P

. Note, that the virtual work done by the nonlin-

ear valve is negative because the ﬂow is directed from the positive terminal

to the negative terminal.

Lagrange’s equations:

150 3 Lagrange’s Equation of Motion

The kinetic coenergy, potential energy and the dissipation function are

∗

= 0, V = (V

− V

+ V

)

/(2C

) + V

/(2C

), and D = 0, respectively.

Lagrange’s equations are

∂T

∗

∂

−

∂T

∗

∂V

∂D

∂

∂V

= e

, (c)

∂T

∗

∂

−

∂T

∗

∂V

∂D

∂

∂V

= e

. (d)

Using the energy relationships, the generalized eﬀorts, and (a) gives

− V

+ V

) = P,

(d) ⇒ −

− V

+ V

) +

= −R

References

1. C. Lanczos, The Variational Principles of Mechanics, vol. 4, 4th ed. Uni-

versity of Toronto Press, 1970.

2. G. W. Ogar and J. J. D’Azzo, “A Uniﬁed Procedure for Deriving the Dif-

ferential Equations of of Electrical and Mechanical Systems,” IRE Trans-

actions on Education, vol. E-5, pp. 18-26, 1962.

3. L. Meirovitch, Methods of Analytical Dynamics, McGraw-Hill, 1970.

4. L. A. Pars, A Treatise on Analytical Dynamics. Heinemann, 1965.

5. R. J. Smith, Circuits devices and systems, John Wiley and Sons, 1976.

6. G. J. Van Wylen and R. E. Sonntag, Fundamentals of Classical Thermo-

dynamics, 3rd ed. Wiley & Sons, 1985.

7. P. E. Wellstead, Introduction to Physical System Modelling, Academic

Press, 1979.

8. D. C. White, and H. H. Woodson, Electromechanical Energy Conversion,

John Wiley & Sons, 1959.

9. J. H. Williams, Jr., Fundamentals of Applied Dynamics, John Wiley &

Sons, 1996.

Problems

1. In Example 3.5, show that the reaction forces at O do not contribute to

the virtual work.

3.3 Applications 151

2. Show that with the proper choice of units for the fundamental variables

the virtual work for all the terms in Table 3.1 have the same units.

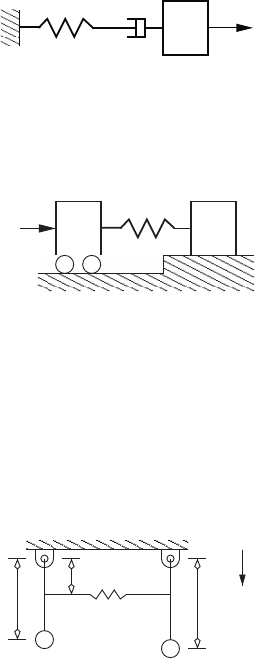
3. Derive Lagrange’s equation for the viscoelastic system shown below.

4. In the system shown here mass m

can move freely while, mass m

subjected to static and kinetic (sliding) friction forces. The coeﬃcient of

static friction is µ

, and the coeﬃcient of kinetic friction is µ

. Derive

Lagrange’s equation of motion for the system.

1 2

5. The pendulum on the left is connected to the pendulum on the right via

nonlinear spring that behaves according to the law

= ky

where f

is the force applied to the spring, k is a constant, and y is

the net deﬂection of the spring. Derive Lagrange’s equations of motion

for this system. Assume small angular displacements for each pendulum,

and that the acceleration due to gravity acts downward as shown.

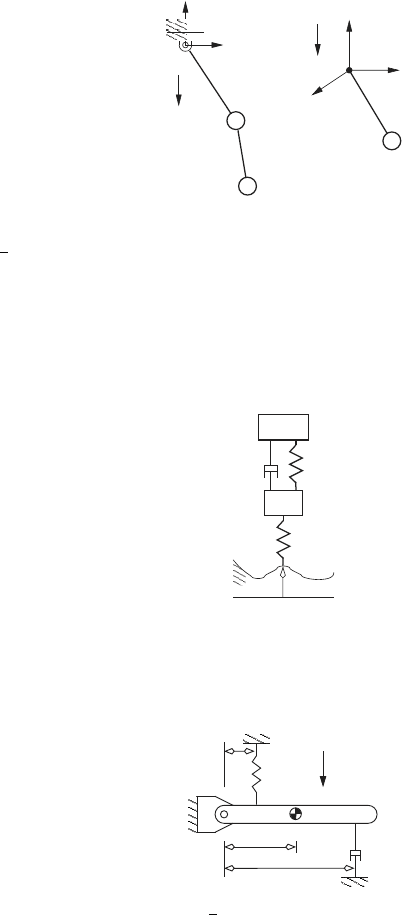
6. Derive Lagrange’s equation for the (a) double pendulum, and (b) the

spherical pendulum shown here. In the case of the double pendulum the

rod l

can rotate about the pivot at O in the x-y plane. The rod l

can

rotate about M

in the x-y plane. For the spherical pendulum the rod,

l, is free to rotate about the x-axis and y-axis simultaneously. Derive

Lagrange’s equation of motion for each system.

152 3 Lagrange’s Equation of Motion

(a) (b)

7. A

-car model is shown in the ﬁgure below. Here, y(t) represents the

proﬁle of the road from a ﬁxed reference. The eﬀective spring stiﬀness of

the tire is k

, and m

is the mass of the tire. The suspension has stiﬀness

k, and damping coeﬃcient b. The variable m denotes one quarter of the

mass of the car. Derive Lagrange’s equation for this system. (Neglect the

horizontal motion of the system.)

8. Derive Lagrange’s equation of motion for the system shown below. Here,

the rod has mass m and moment of inertia I

about its center of mass.

The linear spring has stiﬀness k, and the linear damper has damping

coeﬃcient c. (Assume small small angular displacements for the rod.)

9. The ﬁgure below shows a

-car model. The road proﬁle at the front of

the car is y

(t), and the road proﬁle at the rear of the car is y

(t). Both

measure from the same ﬁxed reference. The front tire has an eﬀective

spring stiﬀness k

, and mass m

. The rear tire has an eﬀective spring

stiﬀness k

, and mass m

. The front suspension has stiﬀness k

, and

damping coeﬃcient b

. The rear suspension has stiﬀness k

, and damping

coeﬃcient b

. The eﬀective mass and moment of inertia for one half of the

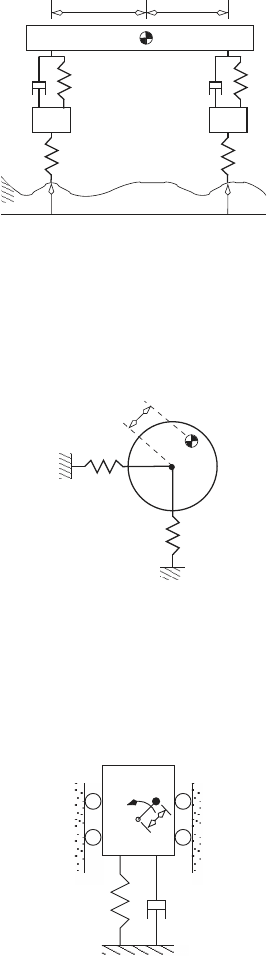
3.3 Applications 153

car are m, and I, respectively. Derive Lagrange’s equation for this system.

(Neglect the horizontal motion of the system.) If the car has a constant

horizontal velocity, v, how are y

(t) and y

(t) related?

I, m

10. The ﬁgure below shows a model of an unbalanced disk (rotor). The disk

is free to rotate about point O, while point O can move in the plane.

The bearings at O have stiﬀness k

in the x-direction, and k

in the y

direction. The rotor has mass m, and moment of inertia I about its center

of mass. Moreover, the center of mass is oﬀset from the geometric center

of the rotor by a distance e. Derive Lagrange’s equation for this system.

I, m

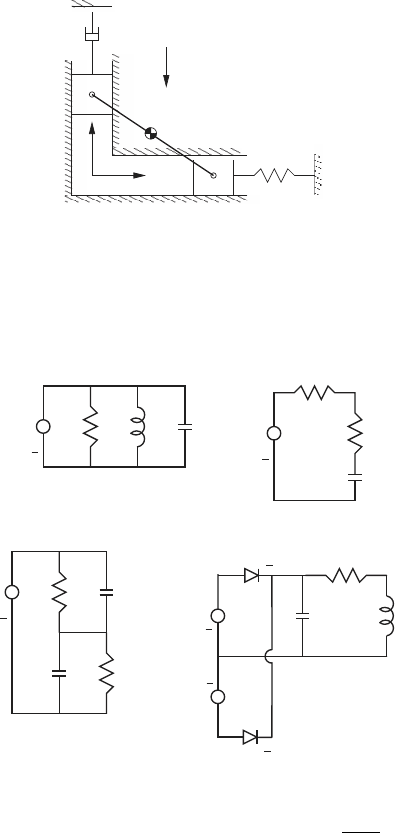
11. The block A has mass m

and is constrained to move in the vertical

direction. Attached to the block is a linear spring with stiﬀness k and a

linear damper with damping coeﬃcient c. The mass m

is also attached

to the block A via a massless rod of length e. The mass m

has a constant

angular velocity ω. Derive Lagrange’s equations of motion for this system.

(Neglect gravity.)

k c

154 3 Lagrange’s Equation of Motion

12. Using generalized displacements (i.e., independent displacements) derive

Lagrange’s equation of motion for the system shown here. The block A

has mass m

, the block B has mass m

, and the rod AB has mass m

and moment of inertia I

about its center of mass. The uniform rod AB

has length l

, and its center of mass is at the geometric center of the rod.

The rod is connected to the blocks via revolute joints.

13. Verify the Lagrange’s equations of motion in Example 3.14.

14. Verify the Lagrange’s equations of motion in Example 3.15.

15. Derive Lagrange’s equation of motion of the systems shown in Examples

3.9, 3.10, 3.11, 3.12, 3.13 and 3.15. In each case include the force(s) due

to gravity in the potential energy instead of the virtual work.

16. Derive Lagrange’s equation for the following electrical circuits.

(a)

v R L C

(b)

v R

(c)

(d)

v (t)

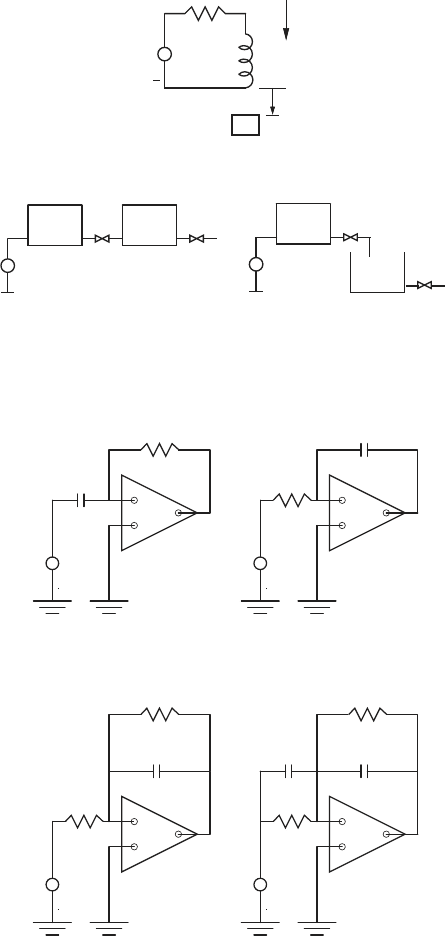
17. Derive Lagrange’s equation for the electromagnetic suspension shown be-

low. Here, the inductance of the coil is given by L =

, where γ

, and

are constants. The variable x is air gap distance between the suspended

mass and the inductor. The acceleration due to gravity acts downward

as shown.

3.3 Applications 155

18. For the ﬂuid systems shown below derive Lagrange’s equation.

C R

(a) (b)

C CR R

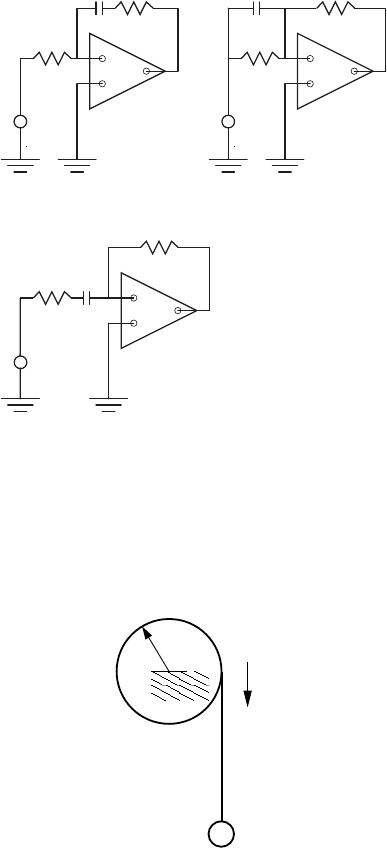
19. Using Lagrange’s equation of motion determine the diﬀerential equation

relating v

and v

for the operational ampliﬁer networks shown below.

(d)

(a) (b)

−

(c)

156 3 Lagrange’s Equation of Motion

(g)

−

R C

−

C R

(e) (f)

20. Derive Lagrange’s equation of motion for the system shown below. In this

system the mass, m, is attached to a cord that is wrapped around the

cylinder that has a radius r. In the position shown the cord has length

. The cylinder is ﬁxed an can not rotate. Also, assume that during the

motion the cord is always in tension.

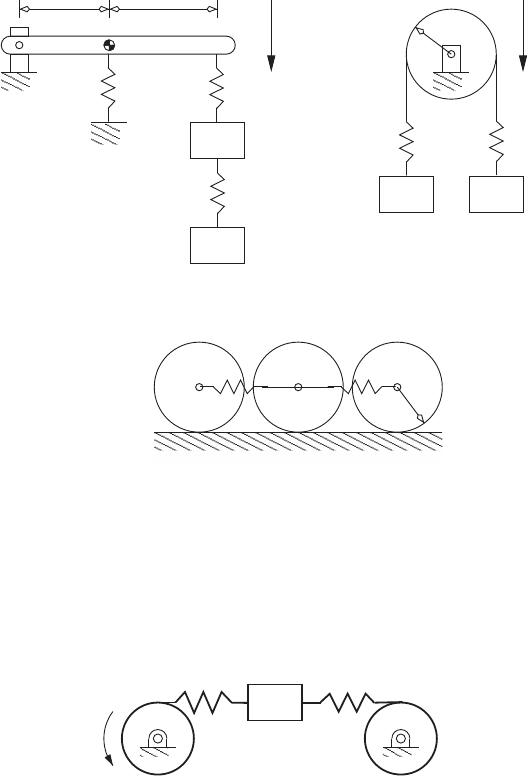
21. Derive Lagrange’s equation of motion for the systems shown below. In (a)

the rod has mass m

and moment of inertia I

about the center of mass.

In (b) the uniform disk has radius r, mass m

and moment of inertia I

about the center of mass. In (c) each of the uniform disks have radius r

and roll without slipping.

3.3 Applications 157

(c)

a b

(a)

(b)

22. The mass m is attached to the ﬂexible belt-pulley system as shown be-

low. Portions of the belt has linear stiﬀness k

and k

. The pulleys have

moments of inertia I

and I

. Each pulley has radius r. A torque τ is

applied to the ﬁrst pulley. In addition the pulley bearings are subject to

linear torsional damping with damping coeﬃcient b. Derive Lagrange’s

equation of motion for this system.

23. Derive Lagrange’s equation of motion for the system shown below using θ

as the generalized displacement. Here, the disk with mass m and moment

of inertia I rolls without slipping on the incline. The linear spring, with

stiﬀness k, is attached to the outer edge of the disk.