Fabien B. Analytical System Dynamics: Modeling and Simulation
Подождите немного. Документ загружается.


48 2 Kinematics
Velocity analysis
The velocity of the point P in the translating frame can be computed from
(2.1) as
0
¯v
QP
=
d
dt
(
0
¯r
QP
) =
d
dt
(
0
¯
R
QQ
1
) +
d
dt
(
1
¯r
Q
1
P
).
Here, the term
d
dt
(
0
¯r
QP
) = ˙x
ˆ
i + ˙y
ˆ
j + ˙z
ˆ
k
is the velocity of P relative to Q as seen from frame 0, the term
d
dt
(
0
¯
R
QQ
1
) =
˙
X
ˆ
i +
˙
Y
ˆ
j +
˙
Z
ˆ
k
is the velocity of Q
1
relative to Q as seen from 0, and the term
d
dt
(
1
¯r
Q
1
P
) = ˙x
1
ˆ
i
1
+ ˙y
1
ˆ
j
1
+ ˙z
1
ˆ
k
1
is the velocity of P relative to Q
1
as seen from frame 1. The term d(
1
¯r
Q
1
P
)/dt
uses the fact that d
ˆ
i
1
/dt = d
ˆ
j
1
/dt = d
ˆ
k
1
/dt = 0, i.e., the unit vectors
ˆ
i
1
,
ˆ
j
1
,
and
ˆ
k
1
, do not change direction.
Using matrix notation the velocity equation takes the form,
0
˙r
QP
=
0
˙
R
QQ
1
+
0
A
1
1
˙r
Q
1
P
, (2.3)
where
0
˙r
QP
= [ ˙x, ˙y, ˙z]
T
,
0
˙
R
QQ
1
= [
˙
X,
˙
Y ,
˙
Z]
T
,
1
˙r
Q
1
P
= [ ˙x
1
, ˙y
1
, ˙z
1
]
T
, and
0
A
1
is the direction cosine matrix relating the translating frame, x
1
-y
1
-z
1
, to
the fixed frame, x-y-z.
Example 2.4.
In Example 2.2 suppose the displacement of Q
1
relative to Q is given by
X
Y
Z
=
a
1
t
2
+ X
0
a
2
t + Y
0
Z
0
,
where a
1
, a
2
, X
0
, Y
0
, Z
0
, are constants, and t is the time. In addition, suppose
the displacement of P relative to Q
1
is defined by
x
1
y
1
z
1
=
ρ cos λt
ρ sin λt
t
,

2.1 Mechanical Systems 49
where ρ and λ are constants.
Then, the velocity of the point P is
0
˙r
QP
=
0
˙
R
QQ
1
+
0
A
1
1
˙r
Q
1
P
˙x
˙y
˙z
=
˙
X
˙
Y
˙
Z
+
cos θ −sin θ 0
sin θ cos θ 0
0 0 1
˙x
1
˙y
1
˙z
1
=
2a
1
t
a
2
0
+
cos θ −sin θ 0
sin θ cos θ 0
0 0 1
−ρλ sin λt
ρλ cos λt
1
=
2a
1
t − ρλ(cos θ sin λt + sin θ cos λt)
a
2
− ρλ(sin θ sin λt −cos θ cos λt)
1
.
2.1.3 A point fixed in a rotating frame
This section considers the kinematics of a point P , that is fixed in a rotating
frame (see Fig. 2.4). As in the previous section we will let the rectangular
coordinate system x-y-z, with origin Q, be a fixed reference frame, while the
rectangular coordinate system x
1
-y
1
-z
1
, with origin Q
1
, will represent the
rotating frame. Throughout this section Q and Q
1
will remain coincident
however, the x
1
-y
1
-z
1
coordinate system is allowed to rotate with respect to
the x-y-z coordinate system. In addition, the point P , is in a fixed position
relative to the x
1
-y
1
-z
1
system. At any instant we let
0
A
1
denote the direc-
tion cosine matrix that relates the x
1
-y
1
-z
1
coordinate system to the x-y-z
coordinate system.
z
1
y
1
z
1
1
x
Q
P
x
y
Q
Fig. 2.4 A fixed point in a rotating frame

50 2 Kinematics
Displacement analysis
Let the unit vectors
ˆ
i,
ˆ
j, and
ˆ
k be aligned with the x, y and z directions,
respectively. Let the unit vectors
ˆ
i
1
,
ˆ
j
1
and
ˆ
k
1
be aligned with the x
1
, y
1
and
z
1
directions, respectively. Then, the position of the point P is given by the
vector
0
¯r
QP
=
1
¯r
Q
1
P
, (2.4)
where
0
¯r
QP
= x
ˆ
i + y
ˆ
j + z
ˆ
k is the vector from Q to P , and
1
¯r
Q
1
P
=
x
1
ˆ
i
1
+ y
1
ˆ
j
1
+ z
1
ˆ
k
1
is the vector from Q
1
to P . Note that Q and Q
1
are
always coincident thus,
0
¯r
QP
and
1
¯r
Q
1
P
are the same vector but with differ-
ent coordinate system representations.
Velocity analysis
The coordinates of the point P in the x
1
-y
1
-z
1
frame are
1
r
Q
1
P
=[x
1
, y
1
, z
1
]
T
.
Then, P has coordinates
0
r
QP
=
0
A
1
1
r
Q
1
P
, in the fixed frame, where
0
r
QP
=
[x, y, z]
T
. In this case the velocity of P , as seen from the fixed frame, is
0
v
QP
=
d
dt
(
0
r
QP
) =
d
dt
(
0
A
1
1
r
Q
1
P
) =
0
˙
A
1
1
r
Q
1
P
. (a)
where
0
v
QP
= [ ˙x, ˙y, ˙z]
T
. Here, we have used the fact that
d
dt
(
1
r
Q
1
P
) = 0,
because P is fixed in the x
1
-y
1
-z
1
frame. Thus, the velocity,
0
v
QP
, is due
solely to the rotation of the x
1
-y
1
-z
1
frame.
We next develop an expression for the matrix
0
˙
A
1
. Since the direc-
tion cosine matrix,
0
A
1
, is orthogonal, we have (
0
A
1
)
−1
= (
0
A
1
)
T
, and
(
0
A
1
)
T
(
0
A
1
) = I, where I denotes the 3 × 3 identity matrix. Therefore,
d
dt
((
0
A
1
)
T
(
0
A
1
)) = (
0
˙
A
1
)
T
(
0
A
1
) + (
0
A
1
)
T
(
0
˙
A
1
) =
d
dt
I = 0. (b)
Let
1
˜ω = (
0
A
1
)
T
(
0
˙
A
1
), then equation (b) implies that
1
˜ω = −(
1
˜ω)
T
.
That is,
1
˜ω is a skew-symmetric matrix, and it has the form
1
˜ω =
0 −ω
3
ω
2
ω
3
0 −ω
1
−ω
2
ω
1
0
. (2.5)
Using the orthogonality property of
0
A
1
it can be seen that
0
A
1
(
0
A
1
)
T
(
0
˙
A
1
) =
0
A
1
1
˜ω =
0
˙
A
1
.
2.1 Mechanical Systems 51
Hence, the velocity of P can be written as
0
v
QP
=
0
A
1
1
˜ω(
1
r
Q
1
P
). (2.6)
Equation (2.6) can be written as a vector equation as follows. Let the vector
0
¯v
QP
= ˙x
ˆ
i+ ˙y
ˆ
j + ˙z
ˆ
k, represent the velocity of P as seen from the fixed frame.
Let the vector
1
¯r
Q
1
P
= x
1
ˆ
i
1
+y
1
ˆ
j
1
+z
1
ˆ
k
1
, represent the position of P relative
to the rotating frame. Finally, define the vector
1
¯ω = ω
1
ˆ
i
1
+ ω
2
ˆ
j
1
+ ω
3
ˆ
k
1
, as
the angular velocity of the rotating frame. Then, from equation (2.6) it can
be seen that
0
¯v
QP
=
1
¯ω ×
1
¯r
Q
1
P
. (2.7)
The vector on the left-hand side of equation (2.7) is in terms of the unit
vectors
ˆ
i,
ˆ
j, and
ˆ
k, while the vector on the right-hand side of the equation is
in terms of the unit vectors
ˆ
i
1
,
ˆ
j
1
, and
ˆ
k
1
. Thus, an appropriate coordinate
transformation is required to equate the terms on either side of equation
(2.7).
Suppose that the position of the point P is given by
0
¯r
QP
=
ˆ
i
1
=
1
¯r
Q
1
P
then, equation (2.7) implies that
d
dt
(
0
¯r
QP
) =
d
ˆ
i
1
dt
=
1
¯ω ×
ˆ
i
1
. (2.8)
Similarly, if the position of P is given by
0
¯r
QP
=
ˆ
j
1
=
1
¯r
Q
1
P
, or
0
¯r
QP
=
ˆ
k
1
=
1
¯r, then
d
ˆ
j
1
dt
=
1
¯ω ×
ˆ
j
1
, (2.9)
d
ˆ
k
1
dt
=
1
¯ω ×
ˆ
k
1
, (2.10)
respectively. Equations (2.8), (2.9) and (2.10) describe the velocities of the
unit vectors
ˆ
i
1
,
ˆ
j
1
, and
ˆ
k
1
, due to the rotation of the x
1
-y
1
-z
1
frame.
Example 2.5.
Point C denotes the center of the disk shown in Fig. (a), and point P is
on the edge of the disk. The disk rotates about the shaft QC with angular
velocity ω
C
. The shaft QC is perpendicular to CP , and it has a fixed angle
α relative to the horizontal plane. The shaft QC also rotates about the line
QZ with angular velocity ω
Z
. The radius of the disk CP is ρ, and the length
of the shaft QC is l. An analysis of the position and velocity of the point P
proceeds as follows.
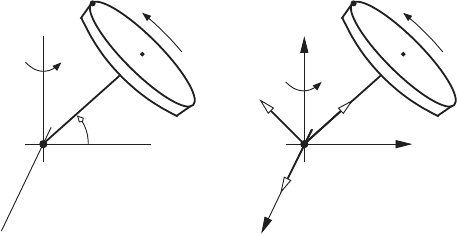
52 2 Kinematics
x
1
1
x
z
1
y
1
P
ω
Q
P
α
ω
Z
Y
Q
Z
(b)(a)
CC
z
ω
Z
C
ω
C
y
Q
First, we establish a fixed reference frame defined by the rectangular co-
ordinates x, y, and z, with its origin at Q. The z axis is along the line QZ,
and the y axis is along the line QY . A right handed rectangular coordinate
system is formed by selecting the x axis perpendicular to the y-z plane, as
shown in Fig. (b). The unit vectors along the x, y, and z axes are
ˆ
i,
ˆ
j, and
ˆ
k, respectively.
Next, a moving (rotating) frame is defined by the rectangular coordinates
system x
1
-y
1
-z
1
, with origin Q
1
that is coincident with Q. This frame is
attached to the disk and undergoes the same rotations as the disk. The unit
vectors along the x
1
, y
1
, and z
1
axes are
ˆ
i
1
,
ˆ
j
1
, and
ˆ
k
1
, respectively.
A vector approach
Displacement analysis
At the instant shown, in the figures above, the relationship between the unit
vectors of the fixed frame and the unit vectors of the rotating frame is
ˆ
i
ˆ
j
ˆ
k
=
1 0 0
0 cos α −sin α
0 sin α cos α
ˆ
i
1
ˆ
j
1
ˆ
k
1
. (a)
Let the vector
0
¯r denote the position of P relative to Q in the x-y-z
coordinate system (i.e., frame 0). Let the vector
1
¯r denote the position of P
relative to Q
1
in the x
1
-y
1
-z
1
frame. Then,
0
¯r
QP
=
1
¯r
Q
1
P
= l
ˆ
j
1
+ ρ
ˆ
k
1
= l(cos α
ˆ
j + sin α
ˆ
k) + ρ(−sin α
ˆ
j + cos α
ˆ
k)
= (l cos α − ρ sin α)
ˆ
j + (l sin α + ρ cos α)
ˆ
k,
where
0
¯r
QP
= x
ˆ
i + y
ˆ
j + z
ˆ
k. Therefore, the coordinates of P in the x-y-z
coordinate system are
2.1 Mechanical Systems 53
x = 0
y = l cos α − ρ sin α
z = l sin α + ρ cos α.
Velocity analysis
Since the x
1
-y
1
-z
1
coordinate system is attached to the disk, the point P
can be treated as a fixed point in a rotating frame. Thus, the velocity of P
is given by
0
¯v
QP
=
1
¯ω ×
1
¯r
Q
1
P
,
where
0
¯v = ˙x
ˆ
i + ˙y
ˆ
j + ˙z
ˆ
k, is the velocity of P relative to the fixed frame, and
the vector
1
¯ω denotes the angular velocity of the rotating frame. From the
problem description it can be seen that
1
¯ω is given by
1
¯ω = ω
C
ˆ
j
1
+ ω
Z
ˆ
k.
The term ω
C
ˆ
j
1
is due to the rotation of the disk about the line QC, and the
term ω
Z
ˆ
k is due to the rotation of the line QC about the line QZ.
Using equation (a) then gives
1
¯ω = ω
C
ˆ
j
1
+ ω
Z
(sin α
ˆ
j
1
+ cos α
ˆ
k
1
) = (ω
C
+ ω
Z
sin α)
ˆ
j
1
+ ω
Z
cos α
ˆ
k
1
. (b)
Hence,
0
¯v
QP
= ((ω
C
+ ω
Z
sin α)
ˆ
j
1
+ ω
Z
cos α
ˆ
k
1
) × (l
ˆ
j
1
+ ρ
ˆ
k
1
)
= (ρ(ω
C
+ ω
Z
sin α) − lω
Z
cos α)
ˆ
i
1
= (ρ(ω
C
+ ω
Z
sin α) − lω
Z
cos α)
ˆ
i.
Therefore, the components of the velocity vector are
˙x = ρ(ω
C
+ ω
Z
sin α) − l(ω
Z
cos α)
˙y = 0
˙z = 0.
A matrix approach
The results given above can also be be obtained using a matrix algebra ap-
proach. Specifically, let the orientation between the x-y-z frame and the x
1
-
y
1
-z
1
frame be given by the direction cosine matrix
0
A
1
. The coordinates of
P in the fixed frame are
0
r
QP
=
0
A
1
1
r
Q
1
P
, (c)
where
0
r
QP
= [x, y, z]
T
,
1
r
Q
1
P
= [0, l, ρ]
T
, and

54 2 Kinematics
0
A
1
=
1 0 0
0 cos α −sin α
0 sin α cos α
.
Thus, equation (c) yields results identical to those obtained above.
The velocity of P is given by
0
v
QP
=
0
˙
A
1
1
r
Q
1
P
=
0
A
1
1
˜ω(
1
r
Q
1
P
), (d)
where
0
v
QP
= [ ˙x, ˙y, ˙z]
T
and
1
˜ω is defined by equation (2.5). The matrix
1
˜ω
contains the coefficients of the angular velocity vector,
1
¯ω = ω
1
ˆ
i
1
+ ω
2
ˆ
j
1
+
ω
3
ˆ
k
1
. From equation (b) it can be seen that
ω
1
= 0,
ω
2
= ω
C
+ ω
Z
sin α,
ω
3
= ω
Z
cos α.
Using these terms in (d) yields the same velocity computed via the vector
approach.
2.1.4 A point moving in a moving frame
This section considers the kinematics of a point that is moving in a frame
that can translate and rotate relative to a fixed frame.
Displacement analysis
Using Fig. 2.2, let the rectangular coordinate system x-y-z, with origin Q,
represent the fixed reference frame. Let the rectangular coordinate system
x
1
-y
1
-z
1
, with origin Q
1
, represent the moving frame that can translate and
rotate with respect to the x-y-z coordinate system. The position of Q
1
with
respect to Q is given by
0
¯
R
QQ
1
= X
ˆ
i + Y
ˆ
j + Z
ˆ
k, where
ˆ
i,
ˆ
j, and
ˆ
k are unit
vectors in the x, y, and z directions, respectively. The position of the point
P relative to Q
1
is given by
1
¯r
Q
1
P
= x
1
ˆ
i
1
+ y
1
ˆ
j
1
+ z
1
ˆ
k
1
, where
ˆ
i
1
,
ˆ
j
1
, and
ˆ
k
1
are unit vectors in the x
1
, y
1
, and z
1
directions, respectively. Then using
vector calculus it can be seen that the position of P with relative to Q is
given by
0
¯r
QP
=
0
¯
R
QQ
1
+
1
¯r
Q
1
P
(2.11)
where
1
¯r
Q
1
P
= x
1
ˆ
i
1
+ y
1
ˆ
j
1
+ z
1
ˆ
k
1
.
Equation (2.11) can be written in matrix form as
2.1 Mechanical Systems 55
0
r
QP
=
0
R
QQ
1
+
0
A
1
1
r
Q
1
P
, (2.12)
where
0
r
QP
= [x, y, z]
T
,
0
R
QQ
1
= [X, Y, Z]
T
,
1
r
Q
1
P
= [x
1
, y
1
, z
1
]
T
, and
0
A
1
is the direction cosine matrix that relates the x
1
-y
1
-z
1
coordinate system
to the x-y-z coordinate system.
Velocity analysis
The velocity of P is given by
0
¯v
QP
=
d
dt
(
0
¯r
QP
)
=
d
dt
(
0
¯
R
QQ
1
) +
d
dt
(
1
¯r
Q
1
P
)
=
˙
X
ˆ
i +
˙
Y
ˆ
j +
˙
Z
ˆ
k + ˙x
1
ˆ
i
1
+ ˙y
1
ˆ
j
1
+ ˙z
1
ˆ
k
1
+ x
1
d
ˆ
i
1
dt
+ y
1
d
ˆ
j
1
dt
+ z
1
d
ˆ
k
1
dt
=
˙
X
ˆ
i +
˙
Y
ˆ
j +
˙
Z
ˆ
k + ˙x
1
ˆ
i
1
+ ˙y
1
ˆ
j
1
+ ˙z
1
ˆ
k
1
+ x
1
(
1
¯ω ×
ˆ
i
1
) + y
1
(
1
¯ω ×
ˆ
j
1
) + z
1
(
1
¯ω ×
ˆ
k
1
)
=
0
˙
¯
R
QQ
1
+
1
˙
¯r
Q
1
P
+
1
¯ω ×
1
¯r
Q
1
P
. (2.13)
Here, the term
0
˙
¯
R
QQ
1
=
˙
X
ˆ
i +
˙
Y
ˆ
j +
˙
Z
ˆ
k is the velocity of Q
1
relative to Q.
The term
1
˙
¯r
Q
1
P
= ˙x
1
ˆ
i
1
+ ˙y
1
ˆ
j
1
+ ˙z
1
ˆ
k
1
is the velocity of P relative to Q
1
.
The term
1
¯ω ×
1
¯r
Q
1
P
is the velocity of P due to the rotation of x
1
-y
1
-z
1
. The
angular velocity of x
1
-y
1
-z
1
is given by the vector
1
¯ω = ω
1
ˆ
i
1
+ ω
2
ˆ
j
1
+ ω
3
ˆ
k
1
.
A matrix representation of the velocity of P can be obtained by differen-
tiating (2.12) to get
0
v
QP
=
d
dt
0
r
QP
=
d
dt
0
R
QQ
1
+
d
dt
(
0
A
1
1
r
Q
1
P
)
=
0
˙
R
QQ
1
+
0
˙
A
1
1
r
Q
1
P
+
0
A
1
1
˙r
Q
1
P
=
0
˙
R
QQ
1
+
0
A
1
1
˜ω(
1
r
Q
1
P
) +
0
A
1
1
˙r
Q
1
P
, (2.14)
where
0
v
QP
= [ ˙x, ˙y, ˙z]
T
,
0
˙
R
QQ
1
= [
˙
X,
˙
Y ,
˙
Z]
T
,
1
˙r
Q
1
P
= [ ˙x
1
, ˙y
1
, ˙z
1
]
T
,
0
A
1
is the direction cosine matrix relating x
1
-y
1
-z
1
to x-y-z, and
1
˜ω is defined in
equation (2.5).
Example 2.6.

56 2 Kinematics
y
1
1
x
z
1
y
1
(b)
z
x
Z
P
C
Q
ω
P
α
ω
Y
(a)
C
Q
Z
X
ω
Z
C
ω
C
B
B
Q
Figure (a) shows a thin disk, with center C, that is attached to the rigid link
BC. The point P is on the edge of the disk, and the line CP is perpendicular
to the line BC. The disk rotates about the line BC with angular velocity ω
C
.
The point B moves in a circular path in the X-Y plane with angular velocity
ω
Z
. The length of QB is l
1
, the length of BC is l
2
, and the radius of the disk
is ρ. The line BC is at a fixed angle α relative to the line QY . A kinematic
analysis of the point P , at the instant shown, proceeds as follows.
First, establish a fixed reference frame. The rectangular coordinate system
x-y-z, with origin at Q, will be used as the fixed reference frame in this
analysis (see Fig. (b)). The x-axis is directed along the line QX, the y-axis
is directed along the line QY , and the z-axis is directed alone the line QZ.
The unit vectors along the x, y, and z axes are
ˆ
i,
ˆ
j, and
ˆ
k, respectively.
Next, a moving frame, x
1
-y
1
-z
1
, is attached to point B such that the origin
of the moving frame, Q
1
, is coincident with B, the y
1
-axis is directed along
the line BC, the x
1
-axis is parallel to the line QX, and the z
1
-axis is selected
to form a right-handed rectangular coordinate system. The unit vectors along
the x
1
, y
1
, and z
1
axes are
ˆ
i
1
,
ˆ
j
1
, and
ˆ
k
1
, respectively.
Displacement analysis
Using the fixed and moving frames described above, the point P can be
treated as a point that us moving in a moving frame. Let
0
R
QQ
1
= [X, Y, Z]
T
be the coordinates of Q
1
relative to Q, in the x-y-z frame. Let
1
r
Q
1
P
=
[x
1
, y
1
, z
1
]
T
be the coordinates of P relative to Q
1
, in the x
1
-y
1
-z
1
frame.
Let
0
A
1
be the direction cosine matrix relating the x
1
-y
1
-z
1
frame to the
x-y-z frame. Then the coordinate of the point P relative to Q in the x-y-z
frame is given by
0
r
QP
=
0
R
QQ
1
+
0
A
1
1
r
Q
1
P
, (a)
where
0
r
QP
= [x, y, z]
T
. For the configuration shown in Fig. (b),
0
R
QQ
1
=
[0, l
1
, 0]
T
,
1
r
Q
1
P
= [0, l
2
, ρ]
T
, and
2.1 Mechanical Systems 57
0
A
1
=
1 0 0
0 cos α −sin α
0 sin α cos α
.
Using these terms in (a) gives
x
y
z
=
0
l
1
0
+
1 0 0
0 cos α −sin α
0 sin α cos α
0
l
2
ρ
=
0
l
1
+ l
2
cos α − ρ sin α
l
2
sin α + ρ cos α
.
Velocity analysis
The velocity of P relative to the fixed frame is
0
v
QP
=
0
˙
R
QQ
1
+
0
A
1
1
˙r
Q
1
P
+
0
A
1
1
˜ω(
1
r
Q
1
P
), (b)
where
0
v
QP
= [ ˙x, ˙y, ˙z]
T
,
0
˙
R
QQ
1
= [
˙
X,
˙
Y ,
˙
Z]
T
, is the velocity of Q
1
relative
to Q in the x-y-z frame, and
1
˙r
Q
1
P
= [ ˙x
1
, ˙y
1
, ˙z
1
]
T
is the velocity of P relative
to Q
1
in the x
1
-y
1
-z
1
frame. The matrix
1
˜ω is given by equation (2.5), and
it contains the coefficients of
1
¯ω = ω
1
ˆ
i
1
+ ω
2
ˆ
j
1
+ ω
3
ˆ
k
1
, which represents the
angular velocity of the moving frame.
For the configuration shown in Fig. (b) we get
0
˙
R
QQ
1
=
−l
1
ω
Z
0
0
,
1
˙r
Q
1
P
=
ρω
C
0
0
, and
ω
1
ω
2
ω
3
=
0
ω
Z
sin α
ω
Z
cos α
.
Here,
0
˙
R
QQ
1
is obtained by noting that Q
1
moves in a circular path with
angular velocity ω
Z
in the x-y plane. The term
1
˙r
Q
1
P
is obtained by noting
that P moves in a circular path with angular velocity ω
C
in the x
1
-z
1
plane.
Finally, the angular velocity of the moving frame is
1
¯ω = ω
Z
ˆ
k = ω
Z
sin α
ˆ
j
1
+
ω
Z
cos α
ˆ
k
1
.
Applying these terms to equation (b) gives
˙x
˙y
˙z
=
−l
1
ω
Z
0
0
+
1 0 0
0 cos α −sin α
0 sin α cos α
ρω
C
0
0
+
1 0 0
0 cos α −sin α
0 sin α cos α
0 −ω
Z
cos α ω
Z
sin α
ω
Z
cos α 0 0
−ω
Z
sin α 0 0
0
l
2
ρ
