Fabien B. Analytical System Dynamics: Modeling and Simulation

Подождите немного. Документ загружается.

18 1 A Uniﬁed System Representation

For mechanical systems in pure translation dampers rep-

resent ideal resistors. Linear dampers behave according to

the law

f = b(v

− v

) = bv,

where f is the force applied to the damper, b is the damping

coeﬃcient, and v = v

− v

is the relative velocity of the

terminals of the damper.

Damper

• Mechanical Rotation:

For mechanical systems in pure translation, torsional

dampers represent ideal resistors. Linear torsional dampers

satisfy the equation

τ = b

(ω

− ω

) = b

ω,

where τ is the torque applied to the damper, b

is the tor-

sional damping coeﬃcient, and ω = ω

−ω

is the relative

angular velocity of the terminals of the damper.

ωω

Torsional damper

• Electrical:

Electrical resistors represent ideal resistors. Linear electri-

cal resistors have a constitutive relationship

v = Ri,

where v is the voltage across the terminals of the resistor, R

is the resistance, and i is the current through the resistor.

Resistor

• Fluid:

The ﬂuid resistors represent ideal resistors in ﬂuid systems.

Linear ﬂuid resistors satisfy the constitutive relationship

P = R

where P is the pressure across the terminals of the resistor,

is the ﬂuid resistance, and Q is the volume ﬂow rate

through the ﬂuid resistor.

Fluid resistor

Content and cocontent

The eﬀort applied by the resistor is related to a scalar function called the

content which is deﬁned as

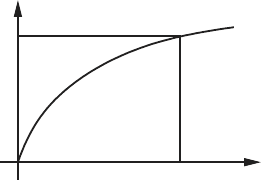
1.2 System Components 19

D(f) =

df = −

e df =

(f) df, (1.16)

where we have used the constitutive relationship e = −e

= −Φ

(f). Hence,

e = −dD(f)/df. Note that the content D(f) is also called the Rayleigh dis-

sipation function.

The cocontent is deﬁned as

∗

) =

−1

) de, (1.17)

where Φ

−1

) = f is the inverse of the function Φ

(f) = e

. An area

representation of the content and cocontent for a nonlinear resistor is shown

in Fig. 1.3. Thus, at any point (e

, f) along the curve Φ

(f) the following

condition must hold,

f = D(f) + D

∗

). (1.18)

The content and the cocontent are both scalar functions, with D(f) indepen-

dent of the eﬀort, e

, and D

∗

) independent of the ﬂow, f.

D(f)

(f)

D (e )

Fig. 1.3 Content and cocontent

If the constitutive relationship Φ

(f) is linear the content and cocontent

will be equal. In particular, consider the case where e

= −e = Φ

(f) = Rf,

where R is a constant resistance, then

D(f) =

(f) df =

Rf df = Rf

/2,

∗

) =

−1

) de

/R) de

= e

/2R = Rf

/2.

The content and cocontent for the linear resistors described above are listed

in Table 1.5.

20 1 A Uniﬁed System Representation

Translation Rotation Electrical Fluid

Content, D(f ) bv

/2 b

/2 Ri

/2 R

Cocontent, D

∗

) F

/2b τ

/2b

/2R P

/2R

Table 1.5 Energy dissipated by linear resistors

1.2.4 Constraint elements

Constraint elements deﬁne kinematic constraint relationships among the sys-

tem variables. These constraint elements can be described as transformers or

transducers.

• Transformers

A transformer transfers energy between the subsystems in the dynamic

system model. These idealized elements do not store, dissipate or generate

energy, and they behave in such a way that the net power into the device

is zero. In the case of transformers the energy transfer takes place within

the same engineering discipline. These elements give rise to displacement

constraints or ﬂow constraints that do no work on the system.

• Transducers

A transducer are similar to a transformer however, the energy transfer

takes place between diﬀerent engineering disciplines. These elements give

rise to displacement or ﬂow constraints that do no work on the system.

Speciﬁc examples of transformers and transducers are given below.

Transformers

• Mechanical Translation:

The lever shown below represents a transformer for mechanical systems

in translation. Here, F

is the force input to left hand side of the lever,

and x

is the corresponding displacement. Similarly, F

is the force input

to right hand side of the lever, and x

is the corresponding displacement.

The lever makes angle θ with the horizontal axis, as shown.

For small displacements the following kinematic relationship holds,

= l

θ → θ = x

= −l

θ → x

= −

1.2 System Components 21

In terms of the velocities these relations become

+ v

= 0,

where v

= dx

/dt and v

= dx

/dt. This equation represents a ﬂow

constraint the lever must satisfy.

Now, summing moments about the pivot (counterclockwise positive) gives,

−F

+ F

= 0,

which is a constraint on the eﬀort variables of the device. As a result, the

power balance yields

Power input + Power output = F

+ F

= (F

−

= 0.

Hence, no energy is stored or dissipated in the device.

• Mechanical Rotation:

The simple gear train shown below represents a transformer for mechani-

cal systems in rotation. The torque input to the left hand gear is τ

, and

is the corresponding angular velocity. Similarly, the torque input to the

right hand gear is τ

, and ω

is the corresponding angular velocity.

Since there is no slipping or backlash the velocity at the point of contact

is r

= −r

. Thus, from the kinematics we have

+ ω

= 0,

which is a ﬂow constraint the simple gear train must satisfy. By summing

the moments about the center of each gear, it can be seen that the force

at the point of contact satisﬁes

which is an eﬀort constraint for the simple gear train. As a result, the

power balance satisﬁes

22 1 A Uniﬁed System Representation

Power input + Power output = τ

+ τ

= (τ

−

)ω

= 0.

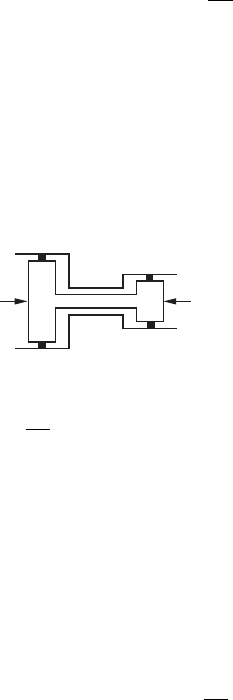
• Electrical:

A schematic of an ideal electrical transformer is shown below. This di-

agram shows two coils that are magnetically coupled via an iron core. The

coil on the left (the primary coil) has N

turns, applied voltage v

and cur-

rent i

. The current in the primary coil creates a magnetic ﬂux φ = N

that induces a voltage v

in the coil on the right (the secondary coil).

Here, the secondary coil has N

turns and current i

. Dots are placed near

one of the terminals in each coil of the transformer to indicate whether

the magnetic ﬂux produced by the coils add or subtract. By convention, if

current enters both dotted terminals the coils will produce magnetic ﬂuxes

that add (Hambley, (1997), p. 686).

i i

v v

It is assumed that there is no ﬂux leakage and the inductance of the coils

can be neglected. Then, a magnetomotive force balance gives,

+ N

= 0,

which is the ﬂow constraint for the device. Also, from Faraday’s law we

have

dλ

d(N

φ)

= N

dφ

dλ

d(N

φ)

= N

dφ

which is the eﬀort constraint that the device must satisfy. The power

balance gives

Power input + Power output = v

+ v

1.2 System Components 23

= (v

−

= 0.

• Fluid:

The diagram below shows a ﬂuid transformer. On the left hand side of

the device the pressure is P

, the volume ﬂow rate is Q

and the area of

the piston is A

. On the right hand side of the device the pressure is P

the volume ﬂow rate is Q

and the area of the piston is A

Using these deﬁnitions the velocity of the piston is Q

= −Q

, or

+ Q

= 0,

which is the ﬂow constraint that the device must satisfy. Moreover, if the

piston is assumed to be massless, the net force acting on the piston is

− P

= 0,

which is a constraint on the eﬀort variables for the device. Finally, the

power balance gives

Power input + Power output = P

+ P

= (P

−

= 0.

Transducers

Some examples of transducer elements are described next. Recall that trans-

ducers are system components that transfer energy from one engineering

discipline to another.

• Mechanical Transducer:

A rack and pinion system shown below is an example of a mechanical

transducer. This device couples a gear (in rotation) with a rack (in transla-

tion). The torque associated with the gear is τ , and ω is the corresponding

angular velocity. The rack has a force F and velocity v.

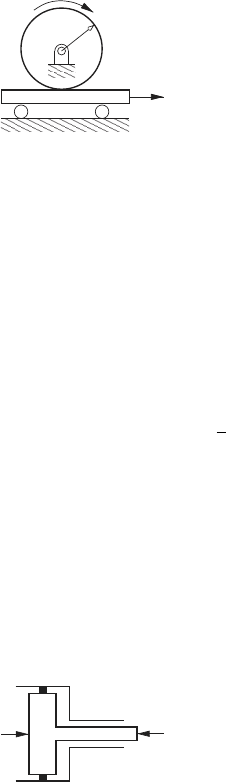
24 1 A Uniﬁed System Representation

If there is no slipping or backlash the system satisﬁes the ﬂow constraint

v + rω = 0.

Moreover, if the system is inertialess, summing the moments about the

center of the gear gives

F r − τ = 0,

which is the eﬀort constraint that must be satisﬁed. The power balance

for the system gives

Power input + Power output = F v + τω

= (F −

τ)v = 0.

• Fluid-mechanical Transducer:

The hydraulic press shown below is an example of a ﬂuid-mechanical trans-

ducer. In this device an incompressible ﬂuid with volume ﬂow rate Q and

pressure P acts on a massless piston with area A. The piston has an applied

force F and velocity v in the direction shown.

It is assumed that the piston does not deform hence, we have

v + Q/A = 0,

which is the ﬂow constraint that the device must satisfy. Since the piston

is massless, the net force acting on the piston is

−F + P A = 0,

which is the eﬀort constraint that the device must satisfy. The power

balance for the system gives

1.2 System Components 25

Power input + Power output = F v + PQ

= (F − AP)v = 0.

1.2.5 Source elements

Power is input to the system via components called sources. These sources

occur in two forms eﬀort sources, e

(t), and ﬂow sources, f

(t). Moreover,

the sources can be ideal sources or regulated sources as described below.

Ideal sources

An ideal eﬀort source will provide the speciﬁed eﬀort to the system irrespec-

tive of the associated ﬂow required by the system. An ideal ﬂow source will

provide the speciﬁed ﬂow to the system irrespective of the associated eﬀort

required by the system. Note that the power available to these ideal sources

is inﬁnite. An example of an ideal eﬀort source is the voltage supplied by a

battery. An example of an ideal ﬂow source is the volume ﬂow rate provided

by a pump. These ideal sources are convenient to use in modeling dynamic

systems. However, it should be noted that they do not exists in reality, since

actual energy sources can not provide inﬁnite power.

The symbolic representations of the ideal sources used in this text are

shown below.

(d)

SourceSource

Effort Flow

e(t)

f(t)

F(t)

Force Torque

τ(t)

(a) (b) (c)

Here, the + sign on the eﬀort source, (a), indicates the positive polarity of

the source. We will use (a) to represent ideal voltage and pressure sources.

The ideal ﬂow source is shown in (b), where the arrow indicates the direction

of positive ﬂow. An applied force is shown in (c), and an applied torque is

shown in (d). In both cases the arrows indicate the direction of positive eﬀort.

Regulated sources

At times it will prove expedient to model certain system elements as con-

trolled or regulated sources. Typically, these devices provide one of the fol-

lowing;

26 1 A Uniﬁed System Representation

1. An eﬀort source that is a function of a ﬂow variable, i.e, a ﬂow regulated

eﬀort source.

2. A ﬂow source that is a function of an eﬀort variable, i.e., an eﬀort regulated

ﬂow source.

3. An eﬀort source that is a function of an eﬀort variable, i.e., an eﬀort

regulated eﬀort source.

4. A ﬂow source that is a function of a ﬂow variable, i.e., a ﬂow regulated

ﬂow source.

Examples of these regulated sources are given below.

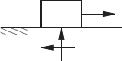
• Coulomb friction

The Coulomb friction force model is often used to describe the force of

interaction between objects. Consider an object moving on a rough sur-

face with velocity v, and let N be the normal reaction force of the surface

acting on the object.

Then the friction force acting on the object can be modeled as follows;

|f| ≤ |µ

N|, v = 0,

f = −µ

Nv/|v|, v 6= 0.

(a)

Thus, when the system is in static equilibrium, i.e., v = 0, the upper bound

on the friction force is |µ

N| where, µ

is the coeﬃcient of static friction.

The magnitude and direction of the static friction force is determined by

the equations of equilibrium.

If there is sliding between the objects, i.e., v 6= 0, then the sliding friction

force has a constant magnitude, µ

N, and acts opposite to the direction

of motion. The constant µ

is called the coeﬃcient of kinetic friction, and

≤ µ

. Hence, the Coulomb friction force can be considered to be a ﬂow

regulated eﬀort source. In this text we call the equations described in (a)

eﬀort constraints. These eﬀort constraint equations provide a relationship

between the eﬀort variables and the ﬂow (or displacement) variables in the

system.

• Diode

A diode can be modeled as an eﬀort regulated ﬂow source. In particu-

lar, let v

represent the voltage (eﬀort) across the terminals of the diode,

and i be the current (ﬂow) through the diode.

1.2 System Components 27

A diode essentially acts as a switch where i > 0 if v

> 0, and i = 0 if

≤ 0. An approximate model for the behavior of the diode is given by

the eﬀort constraint equation

i − I

αv

− 1) = 0,

where I

> 0 and α > 0 are constants that are determined by the material

properties of the diode. The variable I

is called the reverse saturation

current and has a typical value of 1 × 10

−12

amp. The variable α is the

inverse of the thermal voltage, and at room temperature it has a typical

value of 40 1/volt. Hence, the diode can be modeled as an eﬀort regulated

ﬂow source.

We also note that a ﬂuid ﬂow check valve can be modeled as a diode type

device. In this case the ﬂuid ﬂows through the check valve (i.e., diode)

if the pressure drop across the valve is positive. As a result, the ﬂuid

ﬂow through the check valve can be approximated by the eﬀort constraint

equation

Q − Q

αP

− 1) = 0,

where Q

> 0 and α > 0 are constants, and P

is the pressure across the

valve.

• Bipolar Junction Transistor

A bipolar junction transistor can also be modeled as an eﬀort regulated

ﬂow source. The ﬁgure below shows the schematic of a NPN transistor

and a PNP transistor. These devices have three terminals, a base (B), a

collector (C) and an emitter (E).

(a)

NPN Transistor PNP Transistor

(b)

The input-output behavior for these devices can be described using the

Ebers-Moll transistor model (see Jensen and McNamee, 1976, pp. 781). In

the case of the NPN transistor the Ebers-Moll model yields the equiva-

lent circuit shown below. (The Ebbers-Moll model for a PNP transistor is

obtained reversing the current ﬂow directions in the NPN model.)