Fabien B. Analytical System Dynamics: Modeling and Simulation

Подождите немного. Документ загружается.

8 1 A Uniﬁed System Representation

For mechanical systems in pure translation, the point mass

represents the ideal inductor, and for velocities much less

than the speed of light the constitutive equation is given

p = mv,

where p is the linear momentum, m is the mass and v is the

velocity. Note that the point mass or particle only occupies

a point in space, i.e., it does not have any extent.

Point mass

• Mechanical Rotation:

For mechanical systems in pure rotation, the mass moment

of inertia represents the ideal inductor. In this case the

constitutive equation is given by

H = Iω,

where H is the angular momentum, I, is the mass moment

of inertia of the rotor, and ω is the angular velocity.

Rotor

Example 1.1.

As an example consider a uniform thin disk of mass m, and radius r.

Then, the moment of inertia and the angular momentum about the center

of mass of the disk are given by

I =

and H =

ωmr

respectively.

• Electrical:

In electrical systems the inductor represents the ideal in-

ductor, and the constitutive equation is given by

λ = Li,

where λ is the ﬂux linkage, L is the inductance and i is the

current.

Inductor

1.2 System Components 9

Example 1.2.

An example of an electrical inductor is a coil formed by warping a con-

ductor N times around a material with permeability µ. In which case the

inductance is given by

L =

πµd

where d is the diameter of the coil and l is the length of the coil. Hence,

the constitutive equation is λ = πµd

i/4l (Smith, (1976)).

• Fluid:

In ﬂuid systems the ﬂuid inertia represents the ideal in-

ductor, and the constitutive equation is given by

Γ = I

where Γ is the pressure momentum, I

is the ﬂuid inertia

and Q is the volume ﬂow rate.

Fluid inertia

Example 1.3.

Consider ﬂuid ﬂowing in a pipe of length L, and uniform cross-sectional

area A. Let P denote the diﬀerence in pressure at the ends of the pipe, Q

the volume ﬂow rate of the ﬂuid, and ρ the density of the ﬂuid in the pipe.

Then applying Newton’s second law to the ﬂuid in the pipe gives

Force =

(mass × velocity)

P A =

(ρAL × (Q/A))

P =

ρL

Since P = dΓ(t)/dt it can be deduced that the ﬂuid inertia is given by

= ρL/A, and the constitutive equation is Γ = ρLQ/A.

10 1 A Uniﬁed System Representation

Kinetic energy and kinetic coenergy

The energy stored by ideal inductors is called the kinetic energy. Using the

constitutive equation f = Φ

−1

(p) and equation (1.6) the kinetic energy is

deﬁned as

E =

f dp =

−1

(p) dp = T (p). (1.7)

By graphing the constitutive equation for the ideal inductor we can obtain

an area representation of the kinetic energy. Figure 1.1 plots the constitutive

equation for a typical nonlinear inductor and shows the area that determines

the kinetic energy. This ﬁgure also shows the complement of the kinetic en-

ergy, i.e., the kinetic coenergy which is deﬁned as

∗

(f) =

(f) df. (1.8)

From the deﬁnitions of T(p) and T

∗

(f) it can be seen that at any operat-

ing point (p, f) along the constitutive relation Φ

(f) the following condition

holds,

pf = T (p) + T

∗

(f). (1.9)

That is the product of the momentum and ﬂow is equal to the sum of the

(f)

T(p)

T (f)

Fig. 1.1 Kinetic energy and kinetic coenergy

kinetic energy and the kinetic coenergy. It should be noted that the kinetic

energy, T (p), is independent of the ﬂow f, and the kinetic coenergy, T

∗

(f), is

independent of the momentum p. Moreover, both T (p) and T

∗

(f) are scalar

functions.

If the constitutive relation Φ

(f) is linear then the kinetic energy and the

kinetic coenergy are equal. In particular, consider the case where p = Φ

(f) =

If, where I is a constant inductance. Then

T (p) =

−1

(p) dp =

(p/I) dp = p

/2I,

1.2 System Components 11

∗

(f) =

(f) df =

If df = If

/2 = p

/2I.

The kinetic energy and the kinetic coenergy for the linear inductors described

above are presented in Table 1.3.

Translation Rotation Electrical Fluid

Energy, T (p) p

/2m H

/2I λ

/2L Γ

/2I

Coenergy, T

∗

(f) mv

/2 Iω

/2 Li

/2 I

Table 1.3 Kinetic energy and coenergy stored by linear inductors

Finally, note that in its most general form the constitutive equation for

ideal inductors has the representation p = Φ

(q, f, t) which leads a kinetic

energy of the form T = T (q, p, t), and a kinetic coenergy of the form T

∗

(q, f, t). Examples of such relationships will be explored in the following

chapters (see also Problem 5).

Work and energy

Let q(t

) be the displacement of the system at time t

, and q(t

) be the

displacement of the system at time t

, with t

> t

. Then from equation

(1.4) it can be seen that the total work done by an eﬀort in carrying the

system from displacement q(t

) to displacement q(t

) is

q(t

)→q(t

)

q(t

)

q(t

)

e(t) dq(t) =

p(t

)

p(t

)

f(t) dp(t) = T (p(t

)) − T (p(t

)).

(1.10)

Here, p(t

) is the momentum at time t

, and p(t

) is the momentum at time

. Thus, the work done by an eﬀort in displacing the system from q(t

) to

q(t

) is equal to the change in kinetic energy.

1.2.2 Ideal capacitors

Ideal capacitors are system components that store energy. The behavior of

the capacitor element is described by constitutive equations that relate the

displacement and the eﬀort. That is e

= Φ

(q), where e

is the eﬀort

applied to the capacitor, q is the displacement, and Φ

(q) is a continuous,

invertible function that satisﬁes Φ

(0) = 0. The eﬀort the capacitor applies to

the other elements in the system is e = −e

. Since the constitutive equation

is invertible it can be used to obtain the displacement as a function of the

eﬀort, i.e., q = Φ

−1

12 1 A Uniﬁed System Representation

Some examples of ideal capacitors in the various engineering disciplines

are as follows.

• Mechanical Translation:

Springs represent the capacitor elements in translating me-

chanical systems. For a linear spring, the relationship be-

tween the applied force and the deﬂection of the spring is

given by Hooke’s law, i.e.,

f = k(x

− x

) = kx,

where f is the force applied to the spring, k is the spring

stiﬀness, and x = x

−x

is the net deﬂection of the spring.

Mechanical spring

Example 1.4.

Consider the axial deﬂection of a rod with uniform cross-sectional area

A, length L and modulus of elasticity E.

Then the spring stiﬀness is given by

k =

and the constitutive equation is F = EAx/L.

• Mechanical Rotation:

Torsional springs are capacitor elements for mechanical

systems in pure rotation. The linear torsional spring be-

haves according to the relationship

τ = k

(θ

− θ

) = k

θ,

where τ is the torque applied to the spring, θ = θ

− θ

is the net angular deﬂection of the spring, and k

is the

torsional spring stiﬀness.

Torsional spring

1.2 System Components 13

Example 1.5.

Consider a rod with uniform cross-sectional area A, length L and shear

modulus of elasticity G.

Then, the torsional spring stiﬀness of the rod is given by

and the constitutive equation is τ = GAθ/L.

• Electrical:

A linear electrical capacitor behaves according to the equa-

tion

v = q/C,

where v is the voltage applied across the terminals of the

capacitor, q is the accumulated charge, and C is the ca-

pacitance.

Electrical capacitor

Example 1.6.

Consider an electrical capacitor constructed from two plates of area A

and separated by a distance d.

Then, the capacitance is

C =

A

where  is the dielectric constant for the material in the air gap that

separated the two plates. In this case the constitutive equation is v =

qd/(A).

14 1 A Uniﬁed System Representation

• Fluid:

Tanks are the capacitor elements in ﬂuid systems. Linear

ﬂuid capacitors satisfy the equation

P = V/C

where P is the pressure, V is the volume of the ﬂuid and

is the ﬂuid capacitance.

Fluid capacitance

Example 1.7.

Consider a circular cylindrical tank with cross sectional area A, ﬂuid den-

sity ρ and ﬂuid height h.

h ρ

Then the pressure at the bottom of the tank is given by P = ρgh where g

is the acceleration due to gravity. The height of the ﬂuid in the tank can

be written in terms of the volume, i.e., h = V /A. Thus, the pressure at

the bottom of the tank is

P =

ρgV

This implies that the ﬂuid capacitance is given by C

= A/ρg.

Potential energy and potential coenergy

The energy stored by ideal capacitors is called the potential energy, and is

deﬁned as

E =

dq = −

e dq =

(q) dq = V (q), (1.11)

where we have used the constitutive relationship e = −e

= −Φ

(q).

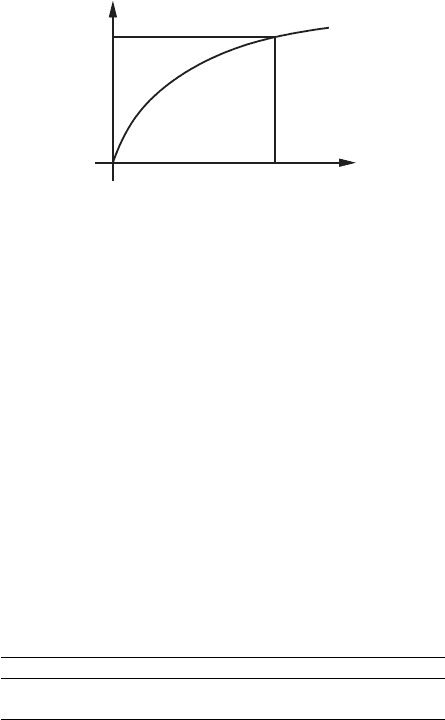
1.2 System Components 15

An area representation of the potential energy is shown in Figure 1.2,

where the complement potential coenergy, V

∗

), is also illustrated. The

potential coenergy is deﬁned as

∗

) =

−1

) de. (1.12)

Thus, at any point (e

, q) along the curve deﬁned by Φ

(q) the following

condition holds,

q = V (q) + V

∗

). (1.13)

That is, the product of the eﬀort and displacement is equal to the sum of the

potential energy and the potential coenergy.

V(q)

(q)

V (eC)

Fig. 1.2 Potential energy and potential coenergy

The potential energy, V (q), and potential coenergy, V

∗

) are both scalar

functions, with V (q) being independent of the eﬀort, e

, and V

∗

) being

independent of the displacement, q.

If the constitutive relation Φ

(q) is linear then the potential energy is

equal to the potential coenergy. In particular, consider the case where e

−e = Φ

(q) = q/C, where C is a constant capacitance, then

V (q) =

(q) dq =

q/C dq = q

/2C,

∗

) =

−1

) de

= Ce

/2 = q

/2C.

The potential energy and the potential coenergy for the linear capacitor ele-

ments discussed above are listed in Table 1.4.

Translation Rotation Electrical Fluid

Energy, V (q) kx

/2 k

/2 q

/2C V

/2C

Coenergy, V

∗

) F

/2k τ

/2k

/2 C

Table 1.4 Energy stored by linear capacitors

16 1 A Uniﬁed System Representation

Work and energy

Suppose the only eﬀort applied to the system is due to an ideal capacitor.

Then from (1.11) the eﬀort can be expressed in terms of the scalar potential

V (q), i.e., e = −dV/dq. Such eﬀorts are called conservative eﬀorts. Let q(t

)

be the displacement of the system at time t

, and q(t

) be the displacement

of the system at time t

, with t

> t

. Then from equation (1.4) it can

be seen that the total work done by an eﬀort in carrying the system from

displacement q(t

) to displacement q(t

) is

q(t

)→q(t

)

q(t

)

q(t

)

e(t) dq(t) = V (q(t

)) − V (q(t

)). (1.14)

Thus, the work done by an eﬀort in displacing the system from q(t

) to q(t

) is

equal to the change in potential energy. However, (1.10) shows that the work

done by any eﬀort is also equal to the change in kinetic energy. Combining

(1.10) and (1.14) we get

q(t

)→q(t

)

= T (p(t

)) − T (p(t

))

= V (q(t

)) − V (q(t

)).

Thus,

T (p(t

)) + V (q(t

)) = T (p(t

)) + V (q(t

)), (1.15)

which is the Principle of Conservation of Energy. That is, if all the eﬀorts

acting on the system are conservative, then the total energy (kinetic energy

plus the potential energy) is a constant.

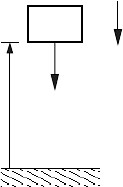
Gravity

The force due to gravity can be written as a potential energy function. For

example, consider the system shown on the right. Here the acceleration due

to gravity acts in the −y direction. The force due to gravity that acts on the

mass, m, is F

gravity

= −mg, as shown.

Datum

−mg

The vertical displacement, measured from the reference or datum is given

by y. Therefore, the work done by the force due to gravity in displacing the

1.2 System Components 17

mass from a height y to the datum 0, is

y→0

e(t) dq(t)

−mg dy

= mgy

= V (y) −V (0),

where V (y) is the potential energy at y and V (0) is the potential energy

at the datum. If we assume that V (0) = 0, i.e., the potential energy at the

datum is zero, then the work done by the force due to gravity is V (y) = mgy.

In addition, it can be seen that

gravity

= −

= −mg.

Hence, the force due to gravity can be determined from the scalar potential

energy function. We also note that the increment in work done by the gravity

force in displacing the object a distance dy is

dW = F

gravity

dy = −mg dy.

1.2.3 Ideal resistors

Ideal resistors are system components that dissipate energy. The behavior of

the resistor element is described by a constitutive equations that relate the

applied eﬀort and the ﬂow. Speciﬁcally, the constitutive equation is given by

= Φ

(f), where e

is the eﬀort applied to the resistor, f is the ﬂow, and

(f) is a continuous, invertible function of f that satisﬁes Φ

(0) = 0. The

eﬀort applied to the other elements of the system by the resistor is given by

e = −e

Some examples of resistors in the various engineering disciplines are as

follows.

• Mechanical Translation: