Ежков В.В., Зарудский Г.К., Зуев Э.Н. и др. Электрические системы и сети в примерах и иллюстрациях

Подождите немного. Документ загружается.

(509,1+743,42)-(-4,12- 10-^+72,307.10-^)220

=239,6 +715,19=240,1Z. 3,63°;

т^=JL _

о А=——' X

- V 4,1210-^-72^53.10-'

^^^^^^ - (-4.12.10-3+7 2,307

•

10-• (239,6+715,19)

= 213,6-726,09=215,2^.-6,96°.

Аналогично вьшолняем расчет напряжений на следующих

итерациях. Все расчеты проведены на персональной ЭВМ

ОПЭВМ). В качестве критерия окончания итерационного процесса

принимаем max|f7J*'-{7f-'"i-maxIA(/f'|<£«. Решение находим

для различных значений точности по напряжению

е^.

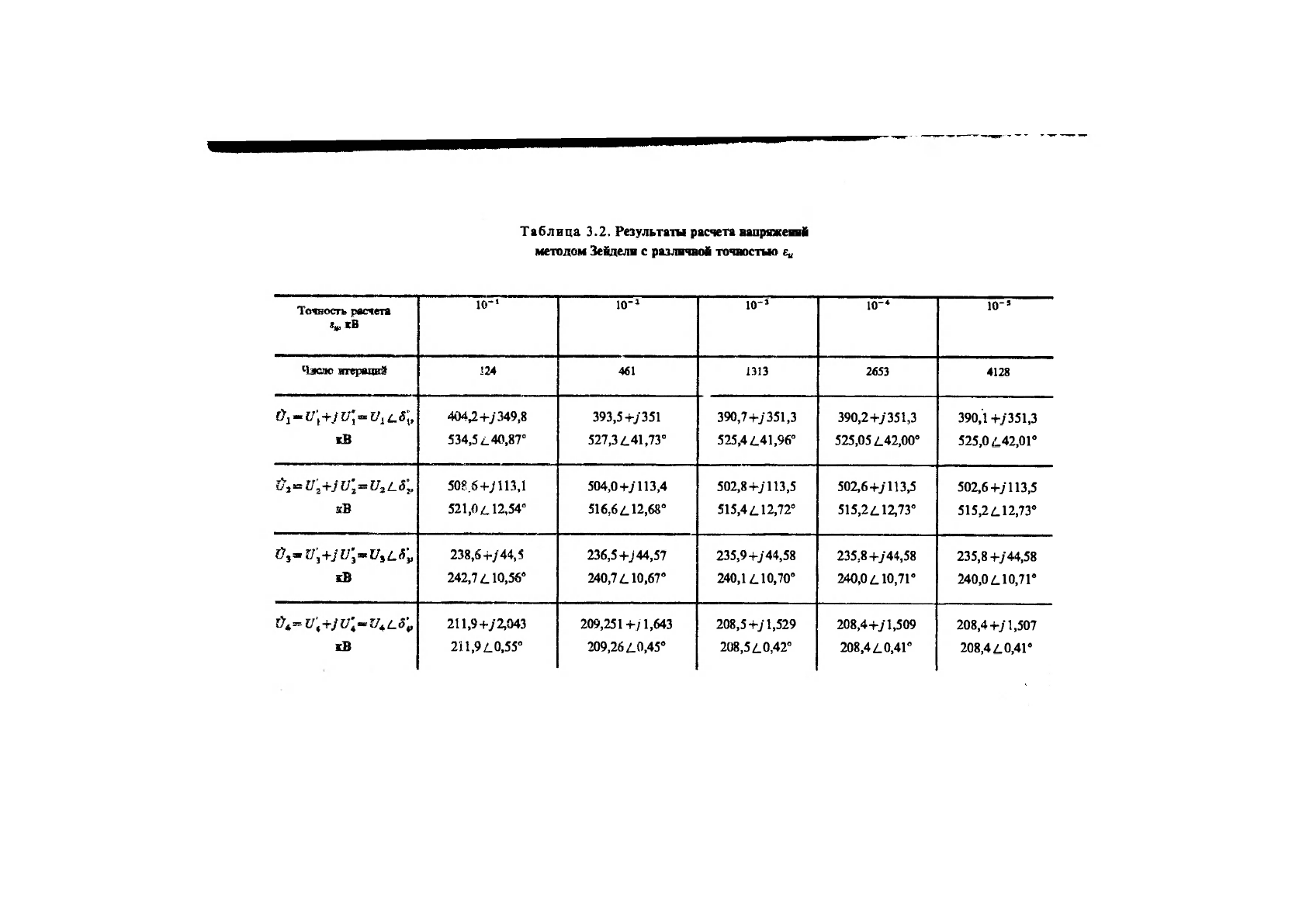
Результаты

расчетов приведены в табл. 3.2. Они показьюают, что метод

Зейделя сходится к решению очень медленно. Повышение точ-

ности расчета на два порядка (с £„=10"^ до £„=10"^) требует i

увеличения числа итераций более чем втрое (с 1313 до 4128). j

Задача 3.4. Используя условия и результаты расчета первой •

итерации задачи 3.3, повторить расчет методом Зейделя при )

учете статических характеристик нагрузок Pa=f{U), Q^=f{U) j

в узлах 3 л 4 схемы рис. 3.1. Сопоставить результаты с резуль-

татами решения задачи 3.3.

Решение. Задаем статические характеристики нагрузок в виде

следующих квадратичных полиномов:

/ V, и' \

flo + ai vr- + .

(3.7)

Qn^Jbo+b,

где flo=0.83; а^- -0,3; ^2=0,47; = -7,0; ^2=4,3.

Так как в задаче 3.3 при выполнении первой итерации в каче-

стве начальных приближений напряжений в узлах 3 я 4 принято

номинальное напряжение, то в соответствии с выражениями (3.6)

мощности нагрузок в этих узлах при выполнении данного расчета

на первой итерации остаются равными заданным значениям. По

результатам расчета напряжений в узлах схемы после первой

итерации в задаче 3.3 определяем новые значения мощностей

нагрузок в узлах 3 и 4 для выполнения второй итерации:

Таблица

3.2.

Результаты расчета вапряжеяяй

методом Зе^еля

разлячвой точвостыв

е^

Точность расчета

'В

10-' 10-^

10-' 10-*

10"»

Часяо этеращй

124 461

1313

2653

4128

кВ

404Д+; 349,8

534,5 £40,87°

393,5+-У

351

527,3/141,73°

390,7+;

351,3

525,4/141,96°

390,2+;351,3

525,05/142,00°

390,1

+;351,3

525,0/142,01°

508.б+Я13,1

521,0/.12,54°

504,0+;

113,4

516,6/112,68°

502,8+;

113,5

515,4/112,72°

502,6+;

113,5

515,2/112,73°

502,6+;

113,5

515,2/112,73°

238,6+/44,5

242,7/110,56°

236,544,57

240,7/110,67°

235,9+;44,58

240,1/110,70°

235,8+;44,58

240,0/110,71°

235,8+;44,58

240,0/110,71°

211,9+y2,043

211,9210,55°

209,251+71,643

209,26/10,45°

208,5+;

1,529

208,5/10,42°

208,4+;i,509

208,4/10,41°

208,4+;

1,507

208,4/10,41°

=70 (0.8З -

0.3

^^+0,47 ^^^ =

74,36

МВт;

GS=40(3.7-7,0^+4.3^)=47,28 Мвар;

p(^=230(0,83-0,3^+0,47^)=226,8 МВт;

\ 220

22(Я У

624=120^3,7-7,0

220 220» у

С учетом статических характеристик нагрузок значения уз-

ловых мощностей Sy3 и ^yj,, входящих в уравнения (3.4),

4З=0-74,36+У(282,6 - 47,28)= -74,36+у235,4 MB-А;

5,4= -226,8-yil6,0 МБ. А.

С учетом полученных значений и выполняются вторая

и последующие итерации, в которых напряжения определяем по

формуле (3.6).

Решение узлового уравнения (3.4) методом Зейделя с учетом

статических характеристик мощности нагрузок получено на

ПЭВМ за 381 итеращ!Ю с точностью е„=10~' кВ. Результаты

расчета следующие:

Номер

Ul. Si.

узла 1 iB

эл. град

кВ

1 533.2

41,07

12,57

402,1

350,1

520,2

41,07

12,57 507,7 113,2

3 242,4

10,59

238,3

44,56

2,94

4 213Д

0,79

213,2

44,56

2,94

Задача 3.5. Записать выражение для определения на каждой

итерации метода Зейделя комплексного значения напряжения

в генераторном узле и реактивной мощности в нем, если узел

задан в форме

Р^—

U^.

Решение. Для генераторного узла i, заданного в форме

Pr—U„ значение бы в формуле (1б) не определено, так

как Qrt не задано.

В этом случае для данного 1-го генераторного узла пред-

варительно находим на к-й итерации напряжение Vf^, определяе-

мое значением только активной мощности в этом узле

Ру1=Рт1~Ря1'

(3.63)

ie\t/r J-1 J-I+I /

имея в виду, что комплексное значение напряжения в этом

(3.9)

Прежде чем найти Of^, находим исходя из того, что

Выполнив ряд преобразований, получаем

Qr+2Q>x+(Vr-Ur)yl С/Г ч'=0, (ЗЛО)

где уи — модуль комплексной проводимости Уе;

— квадрат заданного значения напряжения

в узле;

(з.и)

Решив квадратное уравнение (3.10) относительно Qf\

(3.12)

можно из выражения (3.9) найти комплексное значение напря-

жения в генераторном узле i на данной итерации (ip.

Для всех прочих узлов решение методом Зейделя на каж-

дой итерации выполняется в обычном порядке в соответствии

с формулой (3.6).

Задача 3.о. Решить узловое комплексное уравнение в форме

баланса токов (3.4) методом Зейделя в условиях, когда генера-

торный узел 1 задан в форме

Pj.— U„

а генераторный узел 3 — в

форме Pr-Qr, т. е.

Prt =

1100

МВт;

Uri

= 525 кВ;

Ргз=0 МВт; Сгз=282,6 Мвар.

Значения элементов матрицы Y берем из задачи 3.1, а напря-

жение в балансирующем узле и^, начальные гаиближения напря-

жений Of^ и значения мощностей в узлах Syi (i=2, 3, 4) — из

задачи 3.3.

Решение.

соответствии с алгоритмом, приведенным в зада-

че 3.5, находим значение из вьфажения (3.8):

б,63.10-*-Я.39М0

-S

1100

525

-(-6,63.10-*+у8,115.10"').

500

=573,8+у276,8=

637,1

£25,75".

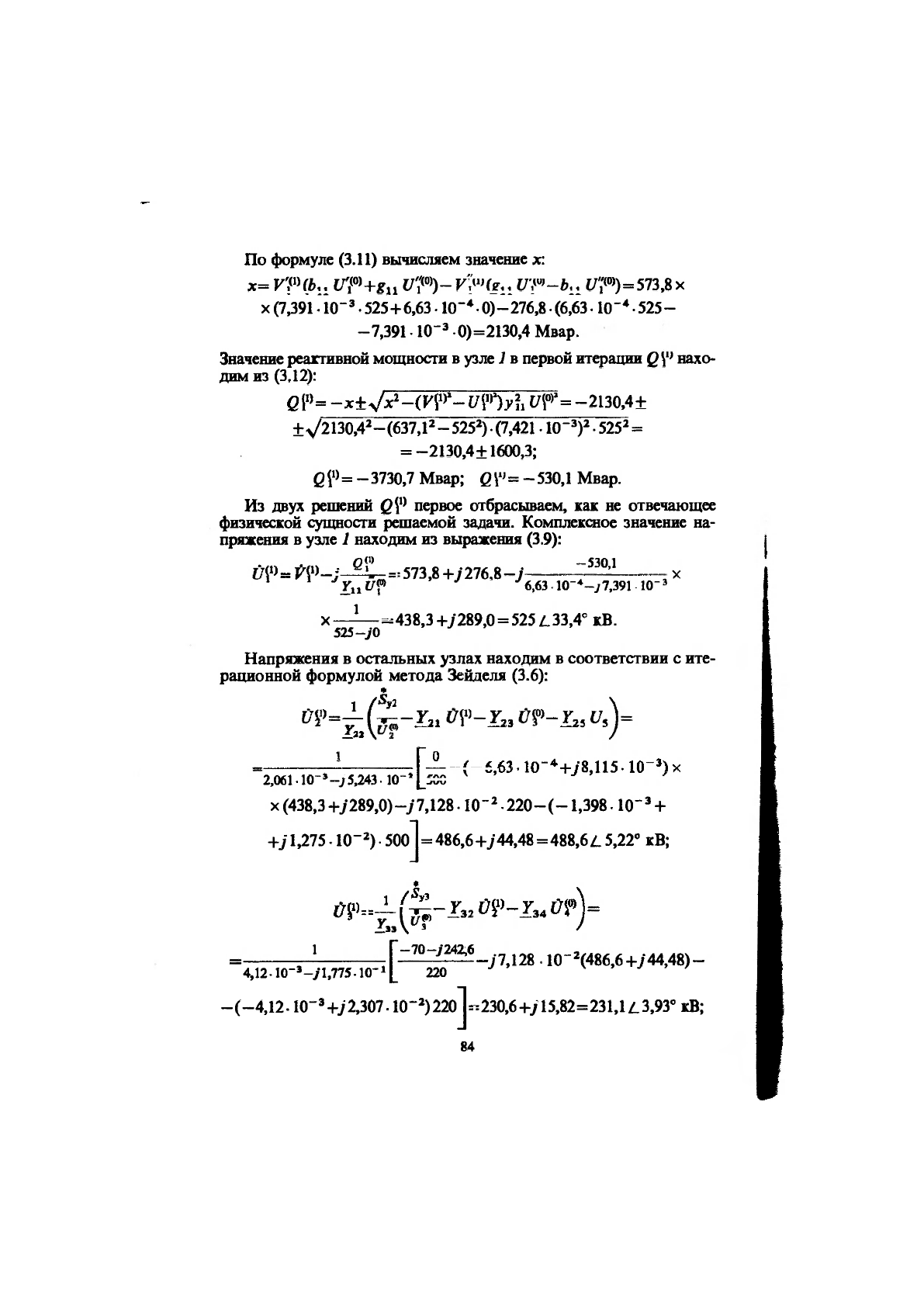
По формуле (3.11) вычисляем значение *:

*= Vi'^+gn f/?')- t/r)=573.8

X (7,391

-10"'

•

525+6,63

• Ю"*-

0)-276,8

• (6,63 • lO"* •

525-

-7,391

•

10-3 •0)=2130,4 j^aap

Значение реагтивной мощности в узле J в первой итерации Q нахо-

дим из (3,12):

C/f = -2130,4±

±V2130,4^-(637,12 -

525^) • (7,421 •

lO-^)^

• 525^

= -2130,4± 1600,3;

ef' = -3730,7 Мвар; 530,1 Мвар.

Из двух решений Q^^ первое отбрасываем, как не отвечающее

физической сущности решаемой задачи. Комплексное значение на-

пряжения в узле 1 находим из выражения (3.9):

.. е?

О)

111

и?

525-J0~

573,8+У276,8-У-

-530,1

6,63.10-'*-у7,391 10"»

=438,3+7289,0 =

525

£33,4" кВ.

Напряжения в остальных узлах находим в соответствии с ите-

рационной формулой метода Зейделя (3.6):

2,061.10-»~/5.243.10"* ^ '

(438,3+У289,0)-У 7,128.10"^-220-(-1,398.10-3 +

+71,275.10-2)-500

= 486,6+у44,48=488,6/. 5,22° кВ;

ТЛ

-7Q-J2A2fi

4,12.10-»-yi,775.10- 220

77,128.10-2(486,6+у44,48)-

-(-4,12.10-Чу2,307.10-^)220

=230,6+у 15,82

=231,1

£3,93° кВ;

4,1210-^-7 72,253.10-»

(-4,12- 10-ЧУ2,307-10-2) (230,6+;15,82)

-230-Л20 , .^-з ^.-оап-, ,n-2

Номер

Ui.

s,.

узла I

эл. град KB

525,00 42,01 390,1

2 515,2 12,73

502,6

3 240,0

10,71 235,8

4 208,4 0,41 208,4

220

= 204,4-j25,4=205,-7,08° кВ.

Далее по приведенному алгоритму вьшолняем вторую и по-

следующие итерадии. Итерационный расчет напряжений, вьшол-

ненный на ПЭВМ с точностью кВ, сошелся за 66 итера-

ций. Результаты расчета следующие:

351,3

113,5

44,58

1,506

С точностью

ДО

погрешностей округления результаты расчета

совпадают с результатами решения задачи 3.3.

На ПЭВМ выполнен расчет напряжений методом Зейделя по

вышеуказанному алгоритму для случая, когда два узла {1 и 3)

заданы в форме Рг— т. е.

Prt = 1100 МВт;

£/^,

525

кВ;

Ргз=0 МВт; Кз=240 кВ.

Решение получено за 64 итерации с точностью е„=10-' кВ

и полностью совпадает с предыдущим.

Задача 3.7. Записать итерационную формулу метода Ньюто-

на, выражения элементов матрицы Якоби и вектора небалансов

токов применительно к расчету напряжений в узлах схемы рис.

3.2, решая узловое уравнение в форме баланса токов в прямо-

угольной системе координат при задании генераторных узлов

в форме Рг—Gr-

Решение. Если уравнения узловых напряжений в форме бала-

нса токов записаны в осях U', U" [выражение (3.S)], то небалансы

активного и реактивного токов в I-M узле имеют вид

^ 4 PyiV.+Qyiir:

(3.63)

•ff

-л-Ь^ ir,

(uy+iV'lf

где1=1 4.

в соответствии с (3.5) обозначим

-lU

(3.14)

{иуниу

Итерационная формула метода Ньютона имеет вид [3.1, 3.2]

дУ/(х

где матрица производных (матрица Якоби)

(3.15)

дХ

дW^ dfVt акт,

адг, dXj sx„

affj dfVj

dfVj

sx. dXj dX„

dw„

dX, dXj dX„

W(X ) — вектор небалансов; ЛХ — вектор приращений неиз-

вестных.

Значения переменных в к-й итерации определяем по формуле

(3.16)

Если во всех узлах схемы заданы активная и реактивная

мощности (все узлы типа

Р^— Qr),

то матрица Якоби может быть

представлена в виде

^aw/' dWf'

av dU'

m,"

dWr"

_5U' 3U'_

(3.17)

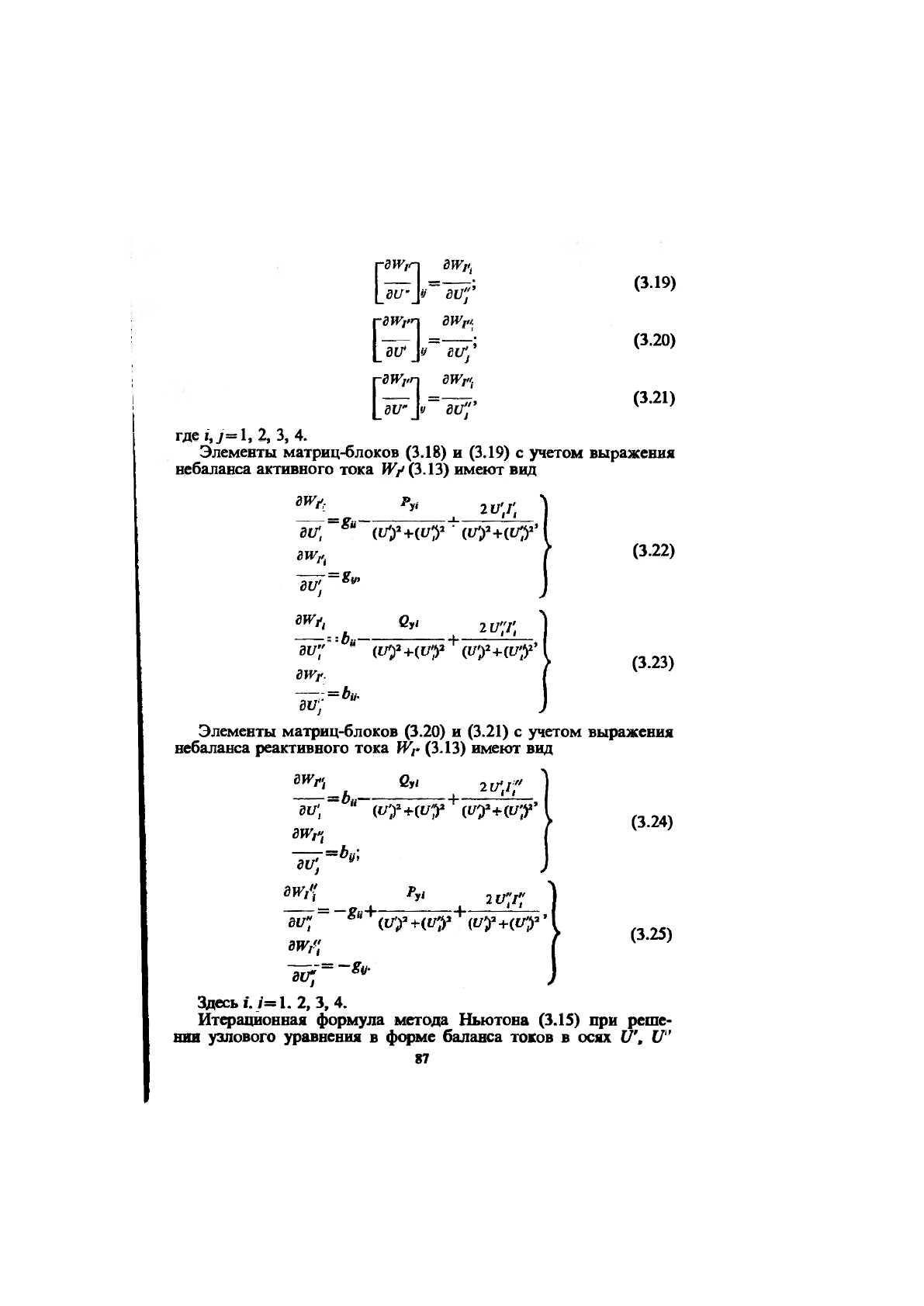
Матрицы-блоки в (3.17) — это квадратные матрицы четвер-

того порядка, элементы которых определяются следующим об-

разом:

rBWf-] bw^i

air/

(3.18)

rdWr^

rdWt»-

SlF

гШрг

BU'

у 8U'j"

dlVpA

BWr'i

« dir;'

(3.19)

(3.20)

(3.21)

где 1,7=

2, 3, 4.

Элементы матриц-блоков (3.18) и (3,19) с учетом выражения

небаланса активного тока

(3.13) имеют вид

dWf.

=gu-

21/',/;

iVfHvy (VfHuy

(3.22)

at;;

^gy.

swt,

lu]'''

dWf.

-bu-

Qy,

их

(3.23)

:=bi.

Элементы матриц-блоков (3.20) и (3.21) с учетом выражения

небаланса реактивного тока Wf (3.13) имеют вид

SHV}

dWt«,

Qy,

eu]

(3.24)

m'!

lU;

= -gv

(3.25)

Здесь 2, 3, 4.

Итерационная формула метода Ньютона (3.15) при реше

НИИ узлового уравнения в фсфме баланса токов в осях U'. U'

к-

в случае задания генераторных узлов в форме Pt—Qt

вмеет вид

swr"

Ш"

ew/"

АХГ*'

ги'_

(3.26)

В качестве критерия окончания итерационного процесса мето-

да Ньютона используем с после-

дующим контролем по критерию max|Af/P|<^.

Задача

ЗЯ. Решить методом Ньютона узловое уравнение (3.5)

в форме баланса токов, записанное в прямоугольной системе

координат (в осях U',

U"),

используя формулы задачи 3.7. Генерг

торные узлы / и 5 заданы в форме Р,—

Gr,

т. е.

Рг1

= 1100 МВт; а, = 34,89 Мвар;

Ргз=0 МВт; 6.3=282,6 Мвар.

Значения элементов матрицы Y берем из задачи 3.1, а напря-

жение в балансирующем узле t/j, начальные приближения напря-

жении Cf* и значения мощностей в узлах (i=

2, 3, 4) — из

задаад 3.3.

Решение. Определяем элементы вектора небалансов токов

Wi(u^''\u на первой итерации на основании выражений

(3.13) (кА):

6,63.

lO-'^.525 + 7,391.10-3

•0

+ (-6,63.10-*.500-

~ • 500 + 5,243.10-^0+

+ (-6,63.525-8,115.10-3.0 + 0.220 - 7,128.10-2.0)-

*3дась H далее используем со1фащенное обозначеше. элемевггов вектора

небалансов н матрицы Якоби (например, Wi), не указывая, что расчет этих

величин гфиводнтся для начальных пртбл^ев^, т. е. на первой итерации.

0-500 + 0 0

1,398.10-^500=-0,017;

500^+0^

С/'з+г'зз

= 7,391.10-^525-6,63.lO-'^.Q+C-g,115.10-^500+6,63.10-''0)-

34,89.525-1100 0

^ = _ 0 Д44;

525^+0»

Qyiir^-Py^V;

_ _2 771.

Определяем элементы матрицы Якобв (3.17) как элементы

матриц-блоков (3.18)

—

(3.21).

В соответствии с выражениями (3.22) элементы матрицы-бло-

awr

ка -~(3.18) (1/Ом):

aw,'^ Pyi 2U\iPy,U\+Qy,U'^

т' 4ri'\2,trr'\3i2 6,63. 10

-4

au\ "" {и'.униу циу+Ю^

1100 2.525(1100.523 + 34,89 0) ,

+ •

awfj