Ежков В.В., Зарудский Г.К., Зуев Э.Н. и др. Электрические системы и сети в примерах и иллюстрациях

Подождите немного. Документ загружается.

51/, 5£/',

=2,061.10 ;

dl/, dU\

dWf^ dWi^

=2,674.

-4

В соответствии с выражениями (3.23) элементы матрицы-бло-

dWf

ка —(3.19)(1/Ом):

0\J

34,894

2.0.(1100.525 +34.894.0)^^^^

525^+0^"^ -/,/Ь4.10 .

-8,115.10-';

51/;- " du

дну, awfj

31/, " 31/,

dWrj

ги", " 51/^

dl/^ Bl/^

=0.1725;

ги'/з aw/,

= -2,307-10-^

В соответствии с выражениями (3.24) элементы матрицы-бло-

dw,"

ка—(3.20)(1/0м):

Bw/\ Gyi 2i/;(Gyit/;-p„i/,)

34.89 2-525(34,89.525-1100 0) „ j

525^+0^ (525^+0»)^

аиу',

= 7,517-10"^

-Г"

-h — -Л

— •

St/;

-Л -

air/;

51/; at/;

SfTfi

su:

= ^4 =

: =

at/'.

dWj-

Qy2 iKiQylU'^-PylV'i

— :+ .. .... =5,243 10-^

=/>32=-7,128.10-2;

dW,'!,

+ . =0,1825;

Tu\

dU'

r = = -2.307.10-^

Qy* 2u',{Qy,U;-Py,U'^

.+ .... =2,01.10"^

в соответствии с выражениями (3.25) элементы матрицы-бло-

^W/y/

ка — (3.21) (1/Ом):

hP;''

fyl

=-6,63.10-

525^+0'

dWt'[

(52540»)»

dW,"^

= -^21 = 6,63.10-^

dw,\

77=

-^31

= 0;

dU\

-^14 =

at/?

-^41=0;

-^22 +

—=-2,061. lo-^

du'^

sw/'

dW/',

-g23-

dU'i

77= -^24 =

-^42=0;

= -

5,55 • 10"

" (l/'з)' + " [(l/y +

-3.

-^44 +

= -8,872.10

-3

Итак, система линеаризованных уравнений на первом шаге

метода Ньютона (3.15) в матричном виде имеет вид

4,65 10-'

-6,63 10

7,517.10-'

-8,115-10-»

-6,63 10-*

2,061.10-»

-8,115.10-»

5,243.10-»

-7,128.10"^

2,674.10-»

-4,12-10"»

-7,128.10-»

0,1825

-2,307.10-»

7.264-10-»

-8,115.10-»

-4,1210-» О

-6,321-10-* О

3,328 10-»

6,63 10-*

-2,307.10-» О

2,01.10-» О

(3.27)

-8,115.10"»

5,243.10"»

-7,128.10"»

6,63.10"*

-2,061.10"»

-7,128.10"»

0,1725

-2,307.10"»

-5,55-10"»

4,12-10"»

-2,307.10"»

0,025

4,12.10"»

-8.872.10"»

-2,079

-0,017

0,318

1,045

-0,244

-0.1

-2,771

-0,427

Систему линейных алгебраических уравнений (3.27) наиболее

рационально решать методом Гаусса. Однако дня повышения

точности решения этим методом желательно, чтобы матрица

коэффициентов системы была диагонально доминирующей. Мо-

8У/Г s^f

жно заметить, что в (3.27) элементы блоков — и — по аб-

ev' 3V'

eW;/ eW/

солютному значению больше элементов блоков и . Что-

du' eu'

бы эти блоки оказались на главной диагонали матрицы Якоби,

переставим столбцы матрицы Якоби, одновременно переставив

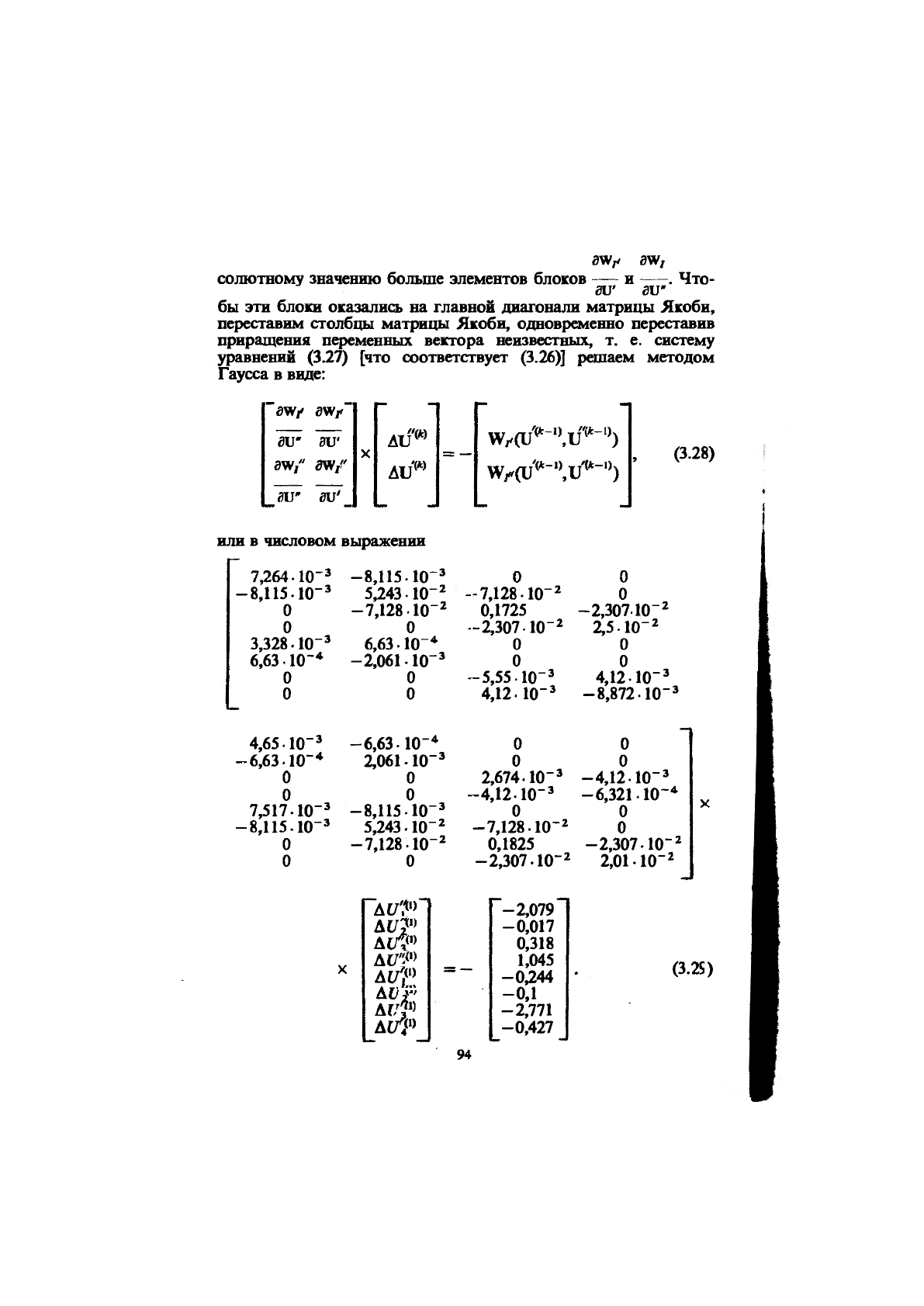
приращения переменных вектора неизвестных, т. е. систему

уравнений (3.27) [что соответствует (3.26)] решаем методом

Гаусса в виде:

"aw/ SSNf~

Ш'

ew/' mf

= —

3U'_

(3.28)

или в числовом выражении

-8,115.10"'

3,328.10"'

6,63.10-*

-8,115.10"'

5Д43 10-2

-7,128.10-2

6,63.10-'^

-2,061.10"'

-7,128.10-2

0,1725

-2,307.10-2

-5,55-10-'

4,12.10"'

-2,30710-2

2,5.10-2

4,12.10"'

-8,872.10"'

4,65.10"'

-6,63. Ю--*

7,517.10"'

8,115.10"'

-6,63

Ю-*

2,061.10"'

-8,115.10-'

5,243.10-2

-7,128.10-2

2,674.10"'

-4,12.10"'

-7,128.10-2

0,1825

-2,307.10-2

-4,12-10"'

-6,321.10--^

-2,307.10-2

2,01 •

10"2

лир

AUT

АС/Я

-2,079

-0,017

0,318

1,045

-0Д44

-0.1

-2,771

-0,427

(3.63)

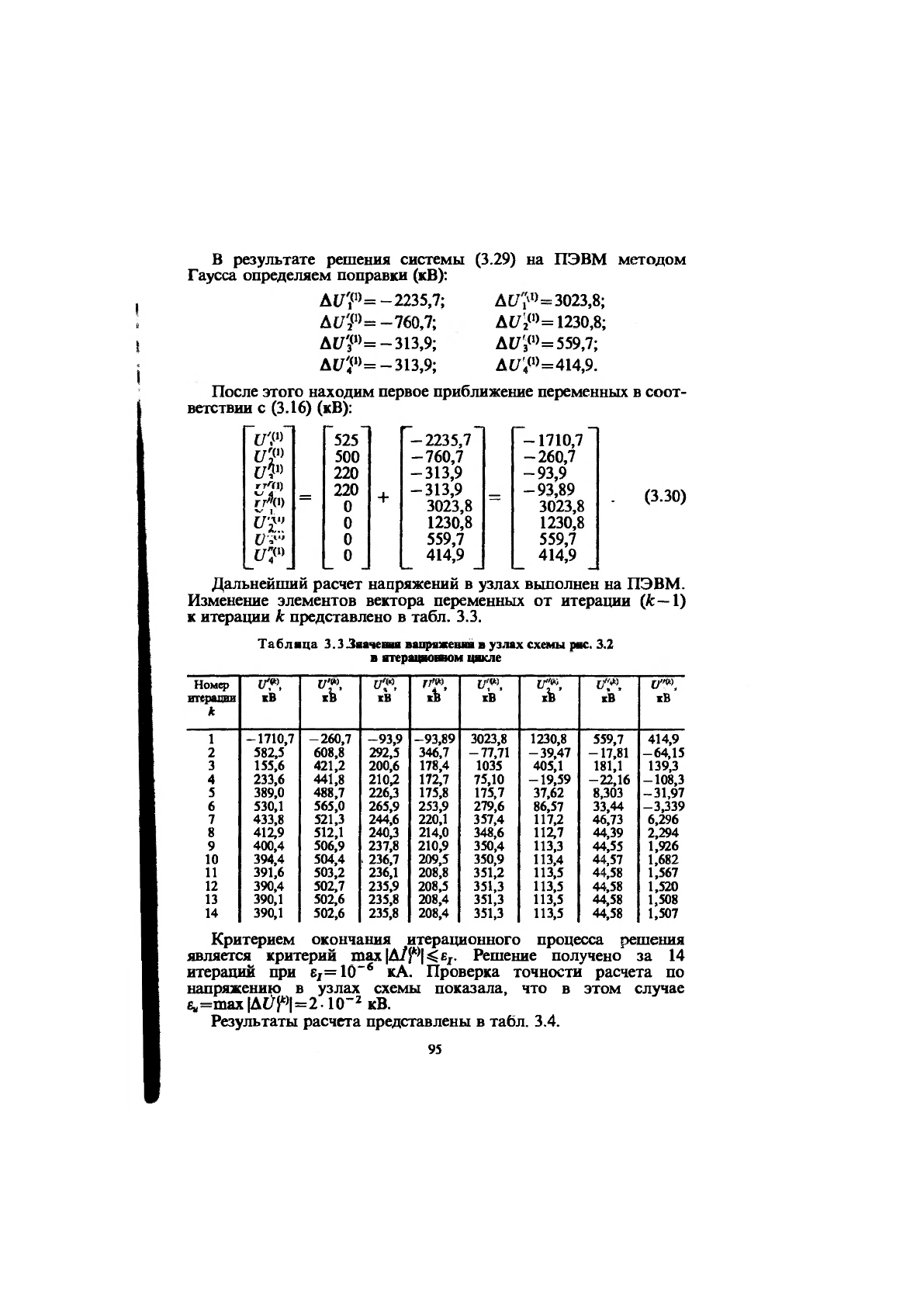
в результате решения системы (3.29) на ПЭВМ методом

Гаусса определяем поправки (кВ):

-2235,7;

А[7;<'>=-313,9;

А[/;<«=-313,9;

3023,8;

АС/2<'>= 1230,8;

А[/з<>)=559,7;

Af/4<»)=414,9.

После этого находим первое приближение переменных в соот-

ветствии с (3.16) (кВ):

и'Р

иГ

и¥

М.)

ит

525

-2235,7

-1710,7

500

-760,7 -260,7

220

-313,9

-93,9

220

-313,9

3023,8

—

-93,89

3023,8

1230,8 1230,8

0 559,7

559,7

0 414,9

414,9

(3.30)

Дальнейший расчет напряжений в узлах выполнен на ПЭВМ.

Изменение элементов вектора переменных от итерации (Л:—1)

к итерации к представлено в табл. 3.3.

Таблица З.ЗЗяачешя вапрвжешш в узлах схемы рис. 3.2

в ятерациопом цикле

HoMq>

жВ

ufK

кВ

хВ А кВ

V'l',

хВ

кВ

l/m

жВ

1 -1710,7 -260,7 -93,9

-93,89

3023,8 1230,8

559,7 414,9

582,5

608,8 292.5

200.6

346,7

-77,71 -39,47 -17,81 -64,15

155,6

421,2

292.5

200.6

178,4

1035

405,1

181,1

139,3

233,6 441,8

210,2

172,7 75,10

-19,59 -22,16

-108,3

389,0

488,7 226,3

175,8

175,7 37,62

86,57

8,303 -31,97

530,1

565,0

265,9

253,9

279,6

37,62

86,57

33,44 -3,339

7 433,8

521,3

244,6 220,1 357,4 117,2 46,73 6,296

412,9

512,1 240,3

214,0

348,6 112,7 44,39 2,294

400,4 506,9 237,8 210,9

350,4 113,3

44,55

1,926

394,4 504,4

236,7

209,5

350,9

113,4 44,57

1,682

391,6

503,2

236,1 208,8

351,2 113,5 44,58 1,567

12 390,4 502.1

235,9

208,5

351,3 113,5 44,58 1,520

390,1

502,6

235,8

208,4

351,3 113,5 44,58

1,508

14 390,1 502,6

235,8

208,4

351,3 113,5 44,58 1,507

Критерием окончания итерационного процесса решения

является критерий шax|A/P|^E^. Решение получено за 14

итераций при Е,=

10~®

КА. Проверка точности расчета по

напряжению в узлах схемы показала, что в этом случае

e«=max|AL/f|=2.10-2KB.

Результаты расчета представлены в табл. 3.4.

Таблица 3.4. Напряжопш • узлах схемы рве. 3.2

пря r*4ifinF¥ узлового ураваеааа в форме бялааса токов

в осях U' и и" методом Ньютова

Номф

К К

Ui.

узла!

iB KB кВ эл. град

390,1 351,3 525 42,01

502,6

113,5 515,2 12,73

235,8 44,58 240,0 10,71

208,4 1,507 208,4 0,41

Задача 3.9.

Записать узловое уравнение в форме баланса мощ-

ностей (3.2) применительно к схеме рис. 3.2 при представлении

комплексных величин:

1. В прямоугольной системе координат (U', (7").

2. В полярной форме (S,

СО-

Решение. Узловое уравнение в форме баланса мощностей

(3.2), записанное для i-ro узла, имеет вид

У (3.31)

где i=

..., 4.

1. Запись комплексного уравнения (3.31) в виде уравнений с дейст-

вительными коэффициентами при представлении комплексных

величин в прямоугольной системе координат (U\ U").

Обозначив комплексные величины

Y=g-jb; 0=U'+jU"; Sy=Py+jQy,

получим уравнение (3.31) в виде

=Pyi-jQyi-(U',-jUb(gi6-jbfs) и,.

Разделив в этом уравнении действительные и мнимые части,

имеем для любого 1-го узла пару уравнений с действительными

коэффициентами:

guim^+iub^+u'» t igijUj+b,u'j)-u7t {byU'j-gyU';)=

= (3.32)

где 1=

2. Запись комплексного уравнения (3.31) в виде уравнений с дейст-

вительными коэффициентами при представлении комплексных

величин в полярной системе координат (5, U).

Обозначаем комплексные величины

C=Uicos5+jan5);

Sy=Py+jQy;

Y=y (sin a—jcos a),

где a=90a

Подставляем комплексные величины в уравнение (3.31), запи-

санное для

1-го

узла, с учетом того, что недиагональные элементы

матрицы Y — это взятые с обратным знаком проводимости со-

ответствующих ветвей:

Yy= -Yi.j=yfi{-sinay+jcosay);

и I

(cos Si—jsin

Si) у a (sin Oj,—у cos

a,;) •

Ui (cos у sin S^+

+ C/j(cos^i—ysin^j) Y, yy(—siaay+jcosaiy)Uj(cosSj+jsinSj)=

J'lJ^i

= Pyt-JQyi-UiicosSi-jsinSdyiei-siaais+jcosae) U^.

Разделив в этом уравнении действительные и мнимые части,

получаем для любого i-ro узла пару уравнений с действитель-

ными коэффициентами:

U^yusinou+U, Ujyysin(Si-Sj-aij)=Py,-UiU6yi6sin{S,-aK);

Ubuco&au-Ui Y, UjyyCOsiSi-Sj-ay)=Qyi+UiU0KCOs(S,-aK),

(3.33)

где i=l, ..., 4.

Задана 3.10. Записать выражения элементов матрицы Якоби,

вектора небалансов мощностей и итерационную формулу метода

Ньютона применительно к расчету напряжений в узлах схемы

рис. 3.2 решением узлового уравнения в форме баланса мощ-

ностей (3.32) в осях U', и" при задании генераторных узлов

в форме: l)Pr-Qr,

Решенне. Если уравнения узловых напряжений в ^рме

баланса мощностей записаны в осях U', U" [выражения (3-32)],

то небалансы активной и реактивной мощности в I-M узле

имеют вид

4-265

Y. (M,u'j+byu"j)-ur'z (byUj-

J-IJ14

J-tJ^i

J-Uf4 J-iMi

(3.34)

где 1= 1,4.

1. Если во всех узлах схемы заданы активная и реактивная

мощности (все узлы типа Р,—

QR),

то матрица Якоби может быть

представлена в виде _

aw,"

вх

dV BV

вщ a^

SV BV

(3.35)

Матрицы-блоки в (3.35) — это квадратные матрицы четвер-

того порядка, элементы которых определяются следующим об-

разом:

BWp,

BW,

BU'

BIVp

BU'

BWq

BU'

'bWQ

BU"

r к

BWp,

BWq,

BW,

BUl'

(3.36)

(3.37)

(3.38)

(3.39)

где i.j=l, 2, 3, 4.

Элементы матриц-блоков (3.36) и (3.37) с учетом выражения

небаланса активной мощности Wp в (3.34) имеют вид

dWp

—=2guU',+ I

(gyU'j+byU'j'i+g^sUe,

(3.63)

dWpi 4

dU'l

dWp

du';

(3.41)

Элементы матриц-блоков (3.38) и (3.39) с учетом выражения

небаланса реактивной мощности

(3.34) имеют вид

dWg. 4

BWq,

(3.42)

dW,

Bu';

BWq,

(3.43)

где 1.7=1, 4.

Таким образом, итерационная формула метода Ньютона

(3.1S) при решении узлового уравнения в форме баланса мощ-

ностей в осях и', и" при задании генераторных узлов в форме

Pt—Qt имеет вид

aw,"

ЗУ}'

8V'

ffWa

dWa

_dV'

3U'_

(3.44)

В качестве критерия окончания итерационного процесса реше-

ния системы нелш1ейных уравнений (3.32) методом Ньютона

использут max|iSi*'—i!S'}*"''|=max|A^J*'|<e, с последующим кон-

тролем по критерию шах lAl^i'^I^E..

2. Если в каком-либо узле т заданы активная мощность

Руя и модуль напряжения (узел типа Р,—С/Д то в системе

узловых уравнений (3.32) вместо уравнения баланса по реактив-

ной мощности для этого узла должно бьпъ записано уршнение

(3.63)