Эськов В.Д., Каталевская А.В., Сипайлов А.Г. Теоретические основы электротехники. Часть 1
Подождите немного. Документ загружается.

91
7. ЦЕПИ С ИСТОЧНИКАМИ НЕСИНУСОИДАЛЬНЫХ
ПЕРИОДИЧЕСКИХ ТОКОВ И НАПРЯЖЕНИЙ
Если в цепи оказываются нелинейные элементы, то и при синусои-
дальном воздействии их реакция будет несинусоидальной с тем же пе-
риодом. В ряде областей науки и техники (автоматика, радиотехника,
телевидение и др.) просто необходимо использование несинусоидаль-
ных периодических сигналов для работы применяемых там устройств.
Поэтому нужно уметь рассчитывать подобные режимы работы
.
Расчет включает в себя три этапа.
1.
Разложение несинусоидальных ЭДС или токов источников в
ряд Фурье.
2. Применение принципа наложения и расчет постоянных и гар-
монических составляющих искомых токов и напряжений.
3. Определение мгновенных или действующих значений иско-
мых величин.
Рассмотрим подробнее каждый из этапов.
7.1. Разложение несинусоидальных периодических
функций в ряд Фурье
Из курса математики известна формула разложения в ряд Фурье
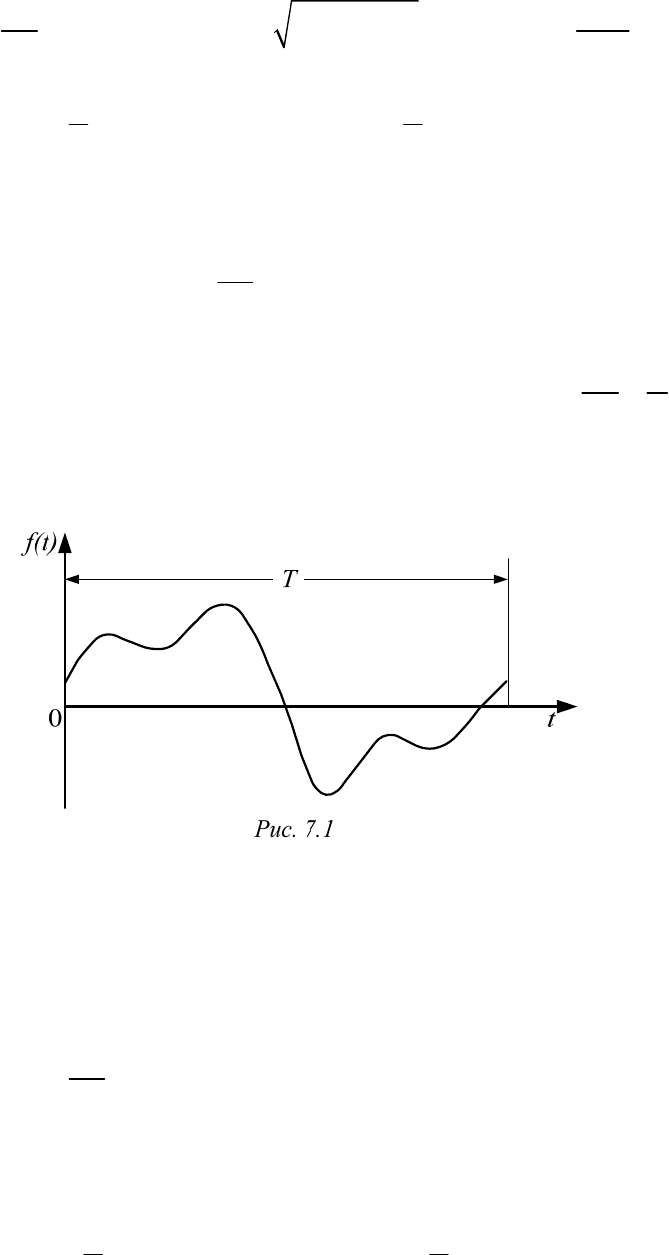
функции времени f(t) с периодом Т (рис. 7.1):
0
1
sin cos ,
km
km
k
f
tA B ktС kt
0
0
21
где ;();
T
A
ftdt
TT
0
2
()cos( ) .
T
km
С ft k tdt
T
В теоретической электротехнике принято использовать иную фор-
му записи:
0
1
sin ,
km k
ft A A kt
0
2
()sin( ) ;
T
km
B
ft k tdt
T
92
22
00
11
причем ()sin( ) ; ()cos
km km
BfkdCfkd
и для сокращения записи введено обозначение
.t
Здесь
0
A
постоянная составляющая,
11
sin
m
A
первая (основ-
ная) гармоника, ее период
2
T
равен периоду самой функции. Все осталь-
ные гармоники называются высшими. Так,
sin( )
km k
Ak
гармоническая
составляющая k-го порядка, (k-я гармоника), чей период
2
.
k
T
T
kk
Каж-
дой гармонике может быть сопоставлена ее комплексная амплитуда:
j.
k
j
km km km km
AAe B C
В реальных условиях приходится иметь дело не с аналитическими
функциями, а с осциллограммами токов и напряжений. В этом случае
применяется приближенное разложение кривых в ряд Фурье с конеч-
ным числом членов, коэффициенты которых определяются по извест-
ным ординатам функций, соответствующим равноотстоящим точкам на
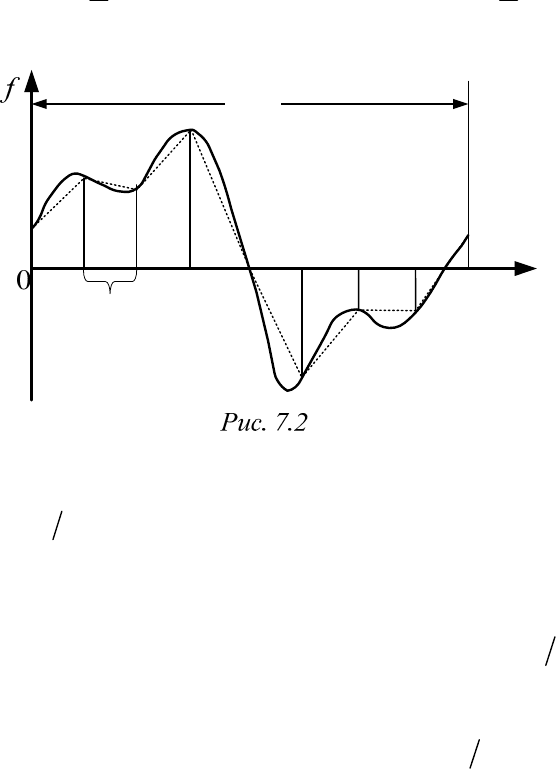
оси абсцисс (рис. 7.2).
Здесь
2
n
интервал между соседними точками деления, чис-
ло которых n (обычно четное).
Приближенное вычисление интегралов (например, по методу тра-
пеций) приводит к следующим формулам:
11
22
()sin( ); ()cos( );
nn
km s s km s s
ss
BfkCfk
nn
2
22
0
0
1
где ( ) ; ; arctg ,
2
km
km km km k
km
C
AfdABC
B
93
0
1
1
(),где 2.
n
ss
s
s
Af s
nn
t
2
При этом можно определить лишь n неизвестных коэффициентов,
поэтому разложение в ряд Фурье может иметь постоянную составляю-
щую и не более
2n
гармоник:
/2
0
1
() sin( ).
n
km k
k
fA Ak
При четном n последняя гармоника (с номером
2)n
содержит
лишь косинусную составляющую, чья амплитуда определяется по фор-
муле с вдвое меньшим коэффициентом перед суммой, чем остальные.
При нечетном – верхний предел суммы равен
(1)2.n
7.2. Частные случаи разложения
Функция, симметричная относительно оси абсцисс,
1,3,5...
( ) ( ) sin( )
km k
k
ff Ak
содержит только нечетные гармоники (рис. 7.3).
Функция, симметричная относительно оси ординат (четная),
0
() ( ) cos( )
km
f
fACk
содержит только косинусные составляющие (без начальных фаз). При-
мер на рис. 7.4.
Функция, симметричная относительно начала координат (нечетная),
содержит только синусные составляющие (без начальных фаз). Пример
на рис. 7.5. Эти свойства функций легко доказываются при анализе фор-
() ( ) sin( )
km
f
fBk

94
мул разложения в ряд Фурье с учетом их особенностей. Разумеется, что
для определения коэффициентов разложения в этих случаях достаточно
учесть равноотстоящие ординаты функций на одной половине периода.
2
7.3. Действующие и средние значения
несинусоидальных величин
Пусть известно разложение некоторого тока в ряд Фурье:
00
sin( ).
kkm k
iIiII k
Найдем его действующее (среднеквадратичное) значение
2
2
0
1
() .
2
I
id
Подставив
()i
в формулу для I и раскрыв скобки в выражении
квадрата суммы, легко убедимся, что интегралы от всех слагаемых, со-
держащих произведения разных гармоник, обращаются в нуль. Дей-
ствительно,
22sin sin
cos cos ,
kn k n
kn kn
ii k n
kn kn
поэтому интеграл от такого произведения за период 2
есть интеграл от
гармонических функций за целое число периодов
()и (),kn kn
который равен нулю. В свою очередь,
2
22
22 2 2
00
00
11
, а
222
km
kk
I
I
dI id I
квадрат действующего значения k-й гармоники. Поэтому
Действующее значение не зависит от начальных фаз гармоник. Его
можно измерить приборами электромагнитной и электродинамической
систем (а действующее значение напряжения – еще и электростатиче-
скими вольтметрами).
2
222
00
.
2
km
k
I
II I I
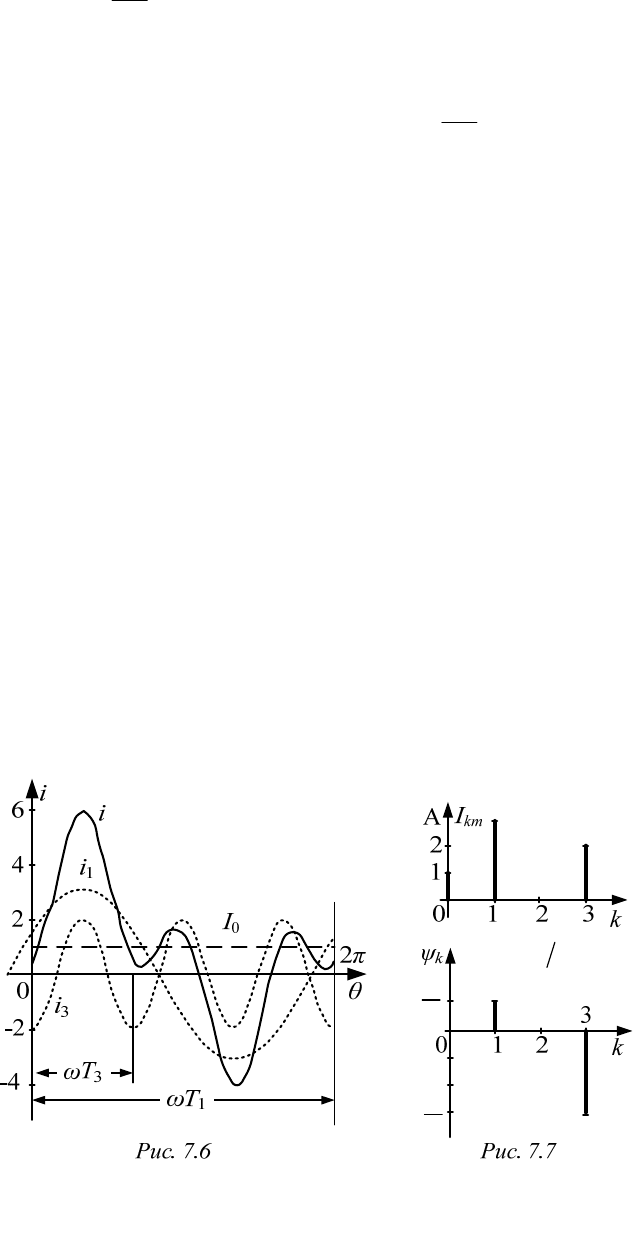
95
Среднее за период значение тока равно постоянной составляющей
в разложении
2
0
0
1
()
2
I
id
и может быть измерено приборами маг-
нитоэлектрической системы.
Среднее по модулю значение тока
2
CP
0
1
|( )|
2
I
id
измеряется
магнитоэлектрическими приборами с выпрямителем.
7.4. Волновые диаграммы и частотные спектры
При построении гармонических составляющих в функции времени
(или
t
) следует иметь в виду, что период k-й гармоники в k раз
меньше периода основной. Во столько же раз уменьшится на графике и
отрезок, соответствующий ее начальной фазе
.
k
Суммируя ординаты
постоянной и гармонических составляющих при одной абсциссе, полу-
чим значение исходной несинусоидальной функции в данный момент
времени. В качестве примера на рис. 7.6 построена функция
1 3sin / 6 2sin 3 / 2 A,i
и ее составляющие.
Совокупность комплексных амплитуд
km
A
всех гармоник данной
функции можно рассматривать как ее дискретный спектр. На графике
он может быть представлен в виде линейчатых амплитудно- и фазоча-
стотных спектров, которые показывают зависимость амплитуд гармо-
ник
km
A
их начальных фаз
k
от номеров гармоник или их частот k
.
t
1
k
2
6
На рис. 7.7 построены спектры функции, волновая диаграмма кото-
рой показана на рис. 7.6.
96
7.5. Коэффициенты, характеризующие форму
несинусоидальных кривых
Наиболее часто употребляются следующие коэффициенты:
коэффициент амплитуды
А
,k
равный отношению наибольшего
значения функции к ее действующему значению,
макс
А
;
F
k
F
коэффициент формы
,k
равный отношению действующего зна-
чения функции к среднему по модулю,
СР
;
F
k
F
коэффициент искажения
И
,k
равный отношению действующего
значения высших гармоник к действующему значению самой функции,
Г
И
;
F
k
F
коэффициент гармоник
Г
,k
равный отношению действующего
значения высших гармоник к действующему значению основной,
Г
Г
1
.
F
k
F
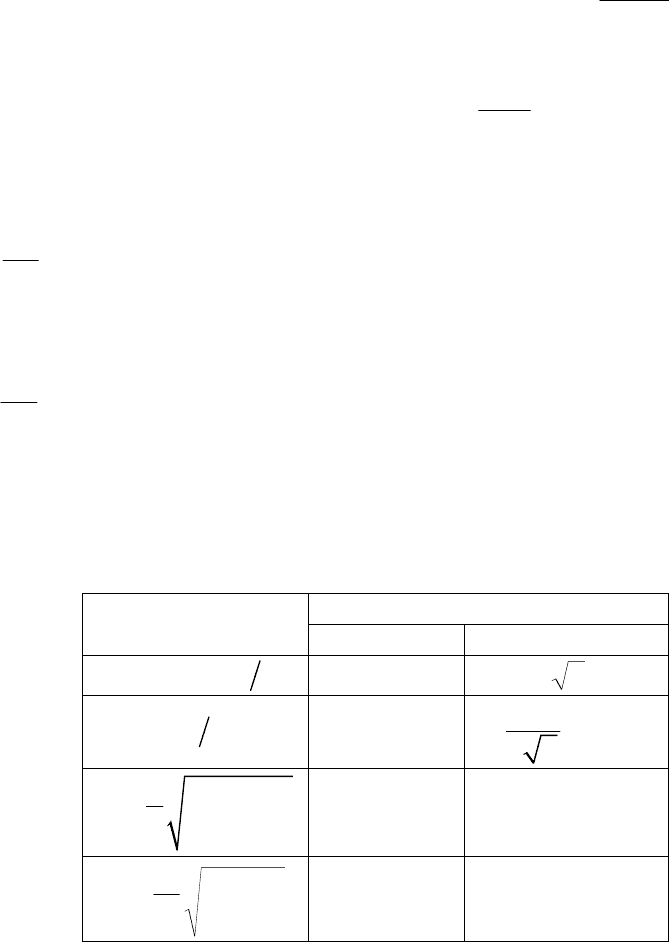
В табл. 7.1 приведены значения этих коэффициентов для постоян-
ного и синусоидального токов.
Таблица 7.1
В
промышленной сети напряжение несколько отличается от сину-
соидального. В стандарте вводят понятие практически синусоидального
напряжения, у которого коэффициент искажения не должен превы-
шать 5 %.
Коэффициент
(формула)
Ток
постоянный синусоидальный
АМАКС
kI I
1
2
СР
kII
1
1,11
22
2
И
2,3...
1
k
k
kI
I
0 0
...3,2
2
1
Г
1
k
k
I
I
k
– 0
97
7.6. Мощность в цепи несинусоидального тока
Пусть ток и напряжение на входе пассивного двухполюсника неси-
нусоидальны:
00
,.
kk
iI i uU u
Тогда мгновенная мощность
00
()( ).
kk
p
ui I i U u
Очевидно,
0
,
k
p
Pp
где
000
,PUI
k
k
k
iup
, за счет наличия
в левой части неравенства произведений величин с разными индексами.
Активная мощность – это среднее значение мгновенной мощности
за период основной гармоники:
2
0
1
2
Ppd
.
Подставляя сюда
pui
и перемножая суммы почленно, легко
убедимся, что интегралы от произведений, содержащих разные гармо-
ники тока и напряжения, обращаются в нуль (как интегралы от гармо-
нических функций за целое число периодов). Остаются слагаемые вида
22
00 00 0
00
11
и cos .
22
kk k k k k
UId UI P uid P UI
Поэтому
2
000
cos ,
kkkknn
PP P UI UI IR
где k – номер гармоники, а n – номер сопротивления. Так что активная
мощность в цепи с источниками несинусоидальных токов и напряжений
равна сумме активных мощностей отдельных гармоник.
По аналогии может быть записана и формула для вычисления реак-
тивной мощности:
sin ,
kkkk
QQ UI
причем понятно, что
0
Q
существовать не может.
Полная мощность S по определению является произведением
действующих значений тока и напряжения:
2222
00
.
kk
SUI U U I I
Очевидно,
222
.SPQ
Коэффициент мощности
Э
cos .PS
Если исследователя интересует лишь энергетическая сторона
процесса, а не гармонический состав тока и напряжения, то реальные
несинусоидальные кривые заменяются эквивалентными синусоидами с
тем же периодом T, теми же действующими значениями тока I и
напряжения U и таким углом сдвига фаз
Э
arccos ,
P
UI
который
обеспечил бы ту же самую активную мощность Р.
98
7.7. Расчет цепей с источниками периодических
несинусоидальных токов и напряжений
Пусть известно разложение в ряд Фурье ЭДС и задающих токов источ-
ников, иными словами, первый этап расчета выполнен. Обычно ряд ограни-
чивают несколькими гармониками, максимальными по амплитуде. В этом
случае каждую из ЭДС можно рассматривать как последовательное соеди-
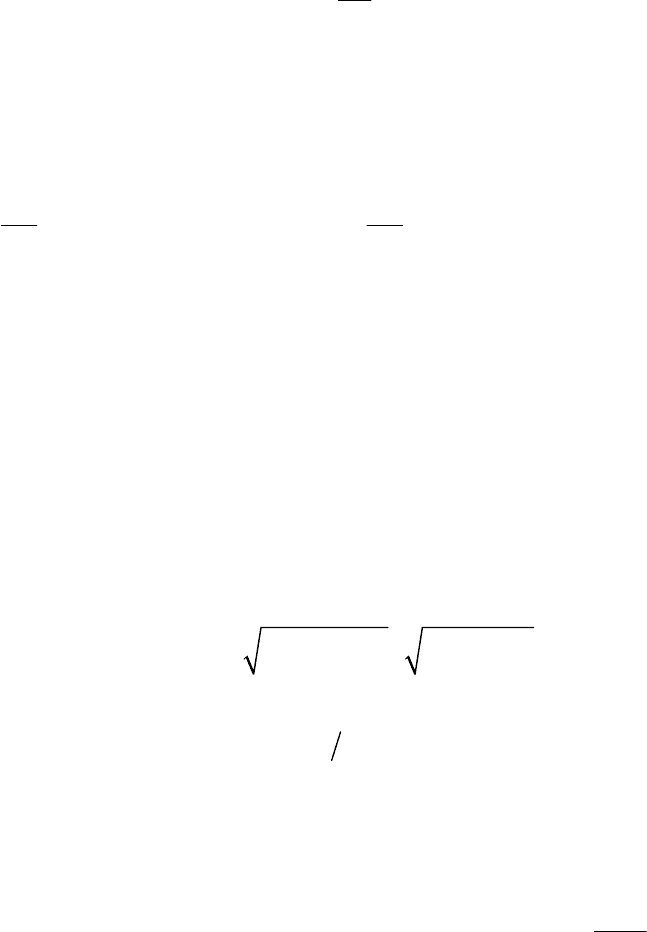
нение нескольких источников напряжения разной частоты (рис. 7.8, а).
А каждый задающий ток можно
представить на схеме в виде параллельного
соединения нескольких источников тока различной частоты (рис. 7.8, б).
Затем на втором этапе применяется принцип наложения (цепь ли-
нейная) и определяются постоянная и гармонические составляющие ис-
комой величины. Разумеется, в подсхеме для постоянной составляющей
индуктивность заменяется закороткой, а конденсатор отключается (раз-
рыв ветви). Расчет гармонических
составляющих ведется комплексным
методом. При этом в комплексную схему для k-й гармоники вместо ин-
дуктивности L включается комплексное сопротивление j
kL, а вместо
емкости C – комплексное сопротивление (j
kC)
–1
.
На третьем этапе мгновенные составляющие искомой величины
суммируются для нахождения ее мгновенного значения или вычисляет-
ся ее действующее значение (в зависимости от условия задачи).
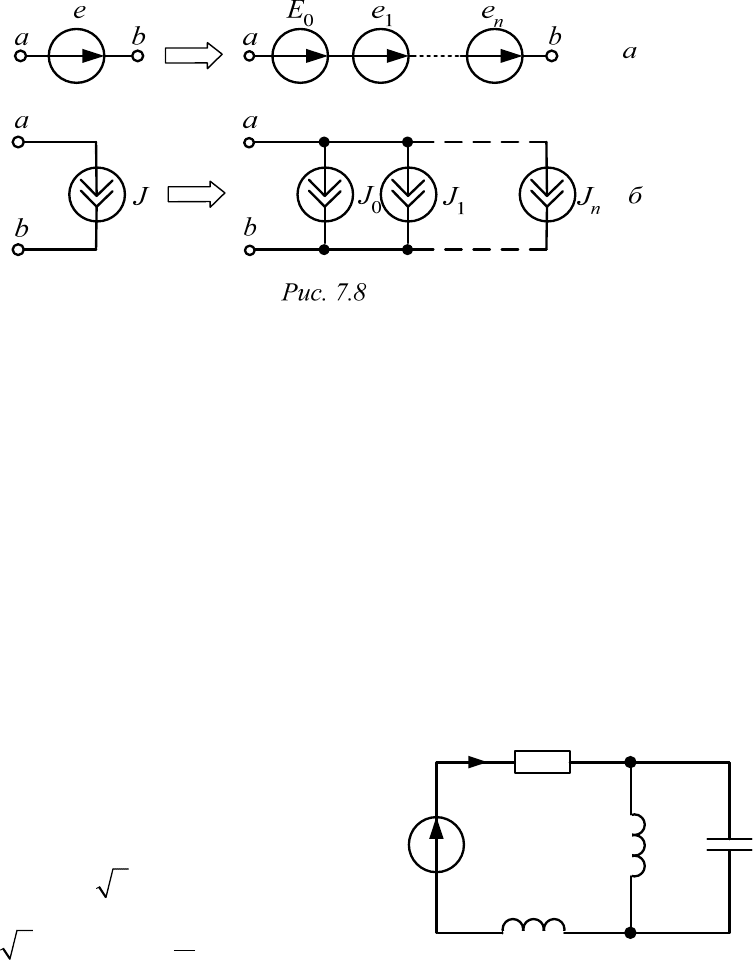
Пример 7.1 (рис.7.9)
0
:
30 Ом;10мГн;
80 мГн; 140 мкФ;
( ) 30 72 2 sin(300 )
54 2 sin 900 В.
2
Дано
RL
L С
et t
t
Рис. 7.9
e(t)
R
L
C
L
0
i(t)
99
Найти: i, P, S.
Решение
Расчет ведем методом наложения.
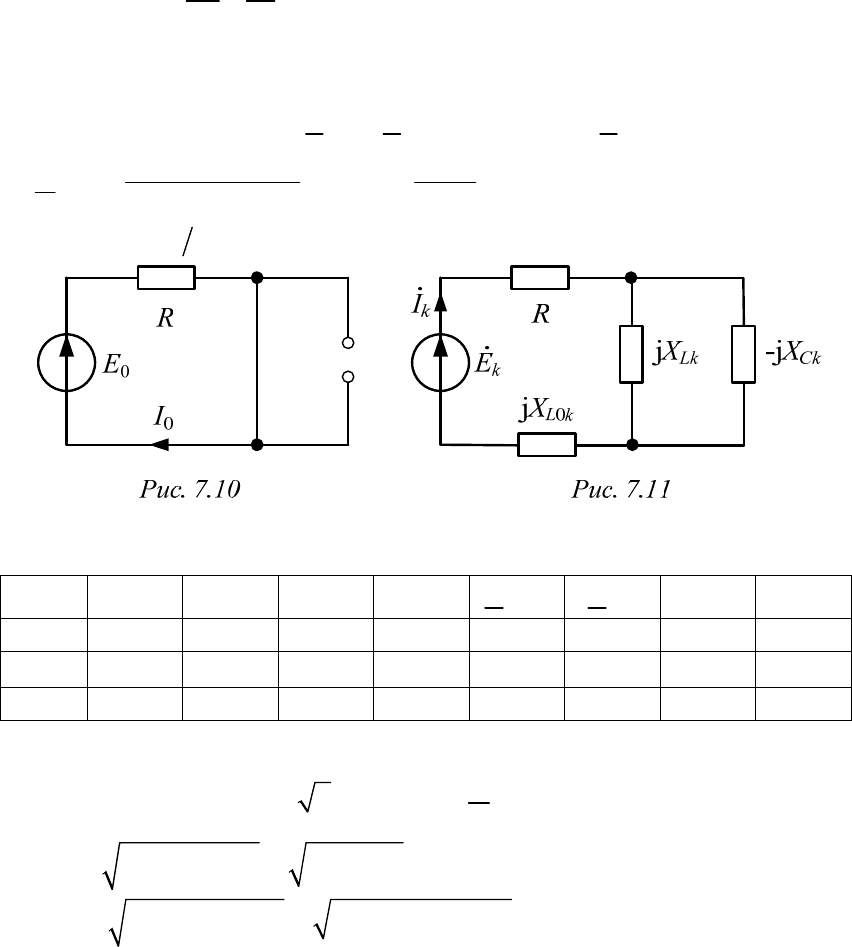
В схеме для постоянной составляющей (рис. 7.10) индуктивности
замкнуты накоротко, а конденсатор отключен. Тогда
2
0
00000
30
1 А;30Вт.
30
E
IPUIIR
R
Гармонические составляющие тока (комплексная схема замещения
для k-й гармоники показана на рис. 7.11) рассчитываются по формулам:
0
Э
/; j ;
э
kk Lk
kk LCk
IEZ Z RX Z
0
0
j(j)
1
;; ;,
jj
Lk Ck
LCk
Ck L k Lk
Lk Ck
XX
Z
Х XkLXkL
XX kC
где
300рад с.
Результаты расчета сведены в табл. 7.2.
Таблица 7.2
k
k
E
0Lk
X
Lk
X
Ck
X
L
Ck
Z
Эk
Z
k
I
k
P
В Ом Ом Ом Ом Ом А Вт
1 72 3 24 24
0 0
3 j54 9 72 8 -j9 30 j1,8 97,2
Таким образом,
013
1 1,8 2 sin(900 ) A;
2
ii i i t
222 2 2
01 3
11,8 2,06A;IIII
222 2 2 2
01 3
30 72 54 95 B;E EEE
22
2,06 30 127,2 Вт.PIR
Нетрудно увидеть, что
013
30 97, 2 127,2 Вт.PP P P
95 2,06 196 В A.SEI
100
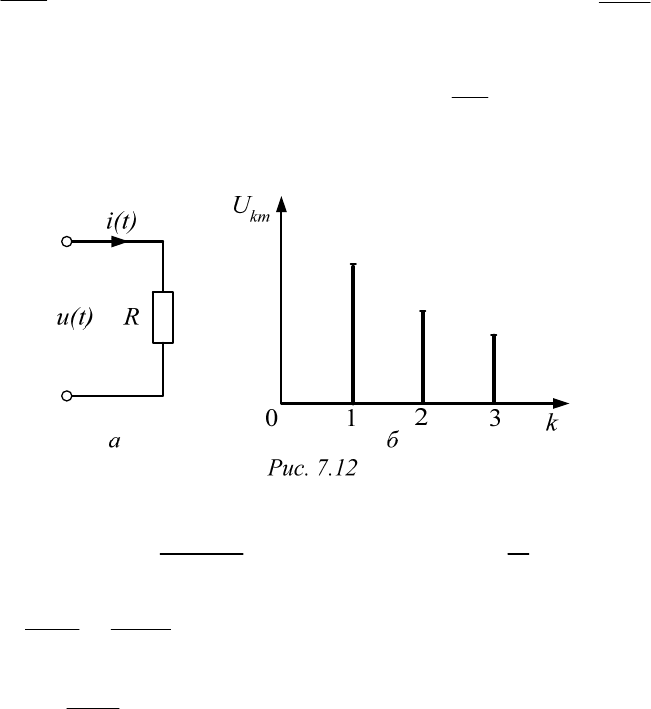
7.8. Влияние характера цепи на форму кривых токов и напряжений
Пусть несинусоидальное напряжение
() sin( )
km k
ut U k
приложено к активному сопротивлению R (рис. 7.12, а). Наличие посто-
янной составляющей
0
U
не изменяет форму кривой, а лишь смещает
эту кривую вверх или вниз относительно оси абсцисс.
Тогда в этом сопротивлении протекает ток
()
() sin( ),
km k
ut
it I k
R
где по закону Ома
.
R
U
I
km
km
Очевидно, кривые i(t) и u(t) подобны. Если же масштаб тока связать
с масштабом напряжения соотношением
,
R
m
m
u
i
то графики ампли-
тудно-частотных спектров тока и напряжения будут совершенно одина-
ковы (рис. 7.12, б).
Если то же самое напряжение подать на индуктивность L
(рис. 7.13, а), то
()
() sin ,
2
km k
utdt
it I k
L
где
;
1L
km
Lk
km
km
kX
U
X
U
I
1
;
Lk L
XkLkX
1
.
L
XL
Если
,
1L
u
i
X
m
m
то при равенстве отрезков, изображающих
1m
U
и
1m
I
на графиках амплитудно-частотных спектров, отрезок
2m
I
(рис. 7.13, б) будет вдвое короче отрезка
2m
U
(рис. 7.12, б), а
3m
I
втрое
короче
3m
U
. Поэтому кривая тока в катушке i(t) окажется больше по-
хожей на синусоиду, чем кривая u(t). Говорят, что индуктивность сгла-
живает кривую тока по сравнению с кривой напряжения. Заметим, что
по катушке может протекать постоянный ток
0
I
, если в остальной части
цепи есть источники этого тока.
Подключим, наконец, к тому же источнику напряжения конденса-
тор С (рис. 7.14, а). Тогда ток в нем
