Эськов В.Д., Каталевская А.В., Сипайлов А.Г. Теоретические основы электротехники. Часть 1

Подождите немного. Документ загружается.

Округленные значения напряжений на входе цепи и на каждом из

индуктивно связанных элементов равны:

● при согласном включении

(20Bдел.; 0,5 A дел.)



139 B; 82 B; 58 B;

ab ad db

UU U U U U  

● при встречном включении

(10Bдел.; 0,25 A дел.)



50 B; 28 B; 32 B.UU U 



Интересно, что в последнем случае напряжение на второй катушке

отстает от тока (так называемый емкостный эффект). Это возможно,

если собственная индуктивность одной из катушек меньше взаимной

индуктивности (в данном примере

).LML

Разумеется, от общего напряжения ток отстает.

5.3. Параллельное соединение

индуктивно связанных элементов

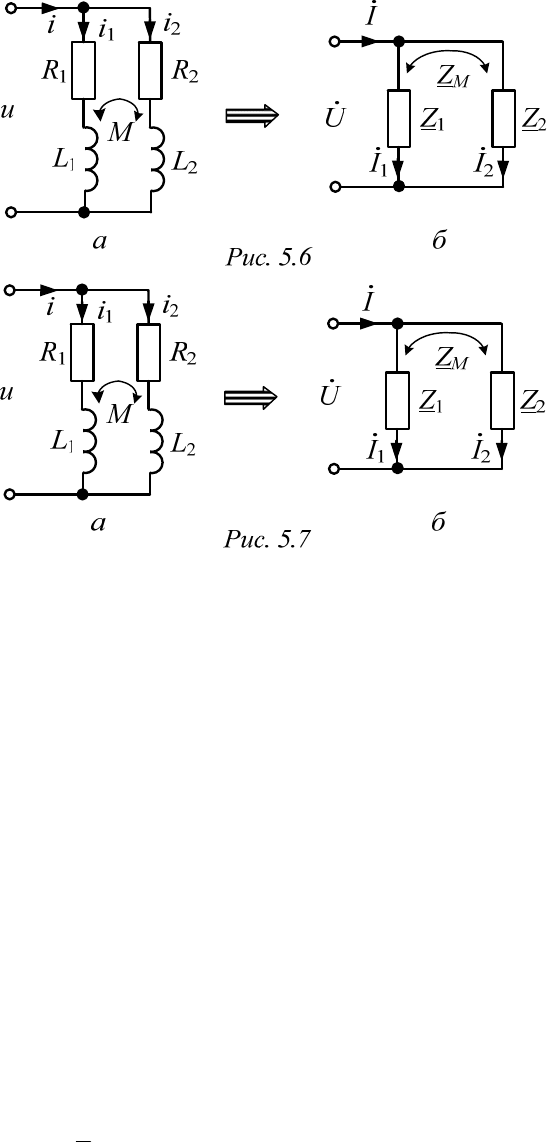
Найдем параметры эквивалентной комплексной схемы замещения

для двух параллельно соединенных катушек при их согласном и встреч-

ном включении (рис. 5.6 и 5.7 соответственно).

По законам Кирхгофа

12 1 2 2 1

;; ,

II I UIZ IZ UIZ IZ    

       

где знак «плюс» соответствует согласному включению, знак «минус» –

встречному,

XRZ 



XRZ





Отсюда легко

найти эквивалентное сопротивление

()

ZZ Z

IZZ Z









Знак «минус» в знаменателе соответствует согласному включению,

«плюс» – встречному. Таким образом, и при параллельном соединении

эквивалентное сопротивление за счет индуктивной связи увеличивается

при согласном включении, уменьшается – при встречном.



5.4. Расчет сложных цепей

с индуктивно связанными элементами

Законы Кирхгофа справедливы и в этих цепях, поэтому порядок

расчета методом уравнений Кирхгофа не отличается, в принципе, от

рассмотренного выше. Нужно только при составлении уравнений по

второму закону учесть наряду с напряжениями самоиндукции и напря-

жения взаимной индукции, применяя правило знаков (см. п. 5.1).

Введение в расчет контурных токов автоматически удовлетворяет

первому закону Кирхгофа, а при составлении уравнений по второму за-

кону действует вышеупомянутое правило знаков. Поэтому порядок рас-

чета методом контурных токов сохраняется, но наличие индуктивной

связи с учетом вышеупомянутого правила вносит две особенности в со-

ставление уравнений с контурными токами.

1. Если один контурный ток протекает по обоим индуктивно

связанным

элементам, то в собственное сопротивление этого контура

нужно добавить

со знаком «плюс», если ток ориентирован оди-

наково по отношению к их одноименным зажимам, и со знаком «ми-

нус», если ориентация различна.

2. Если два контурных тока протекают по двум индуктивно

связанным элементам (каждый в своем), то в общее сопротивление

этих контуров нужно добавить

со знаком «плюс», если токи ори-

ентированы одинаково по отношению к одноименным зажимам своих

элементов, и со знаком «минус», если по-разному.

Разность потенциалов на зажимах каждой из двух ветвей, в кото-

рых имеются индуктивно связанные элементы, выражается через токи

обеих ветвей. Поэтому в общем случае нельзя достаточно

просто выра-

зить эти токи через потенциалы соответствующих узлов. Следователь-

но, метод узловых потенциалов в канонической форме неприменим.

Мы рассматриваем линейные цепи с индуктивной связью, поэтому

метод наложения применим без ограничений (фактически сами поня-

тия индуктивности и взаимной индуктивности введены в соответствии с

принципом наложения). Следует, однако, учесть, что формулы для

эк-

вивалентных преобразований существенно усложняются и их комбина-

ция с методом наложения теряет перспективу применения в расчетах.

Метод эквивалентного генератора, очевидно, применим лишь в

том случае, когда нет индуктивной связи между выделенной ветвью и

одной из ветвей остальной части цепи, которая рассматривается как ак-

тивный двухполюсник.

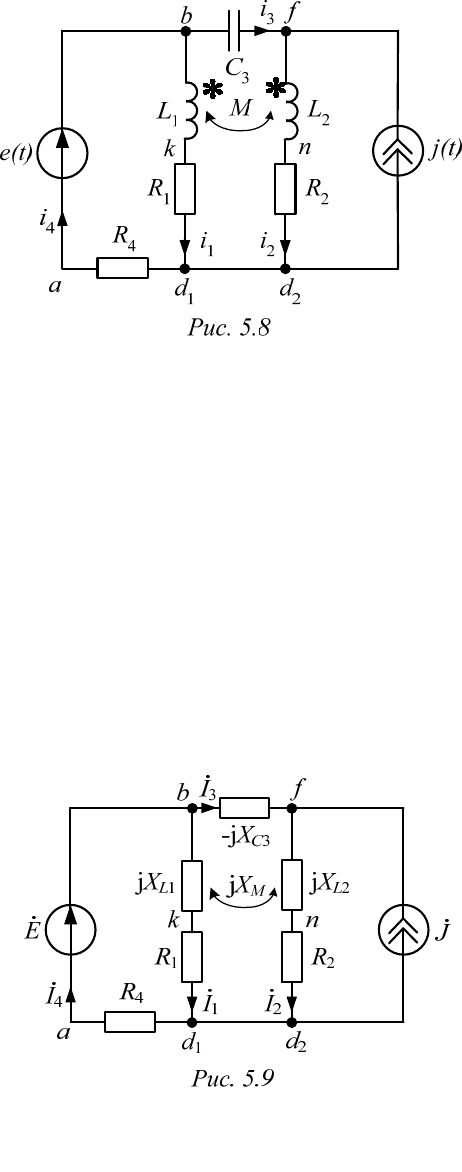
Пример 5.2 (схема на рис. 5.8)

: ( ) 186,6 2 sin( ) B; 123 Ом;

Дано et t R







50 Ом;RR

() 2sin( ) A;jt t





86,6 Ом;



2 200 Ом.

XX

Записать независимые уравнения по законам Кирхгофа (для мгно-

венных и комплексных значений токов и напряжений), рассчитать то-

ки в ветвях, составить баланс мощностей, построить векторную диа-

грамму.

Решение

Составляем уравнения второго закона Кирхгофа для двух незави-

симых контуров (среднего и левого), обходя их по часовой стрелке.

dbfd:

12 21

11 1 3 2 2 2

di di di di

Ri L M idt L M R i

dt dt C dt dt

      



;

daba:

).(

144

teiR

LiR 

Заметим, что согласно правилу знаков напряжения само- и взаимо-

индукции каждого из элементов имеют одинаковые знаки (токи ориен-

тированы одинаково по отношению к одноименным зажимам).

По первому закону Кирхгофа для двух верхних узлов имеем:

143

 iii

; f:

.0)(





tjii

Итого четыре уравнения с четырьмя неизвестными токами.

Для комплексной схемы (рис. 5.9) те же уравнения принимают вид:

111 2 32 22 1

111 244

341

(j)j j (j)j 0;

(j)j ;

LMC L M

RXIXI XI R XI XI

RXIXIRIE

III

IIJ



      

















  







Подстановка числовых значений коэффициентов дает:

123

124

341

( 123 j100) (50 j13,4) j86,6 0;

(123 j200) j100 50 j186,6;

III





 





















Решение этой системы позволяет найти комплексные токи:

Напряжение на зажимах источника тока

Комплексная, активная и реактивная мощности источников:

И 4

€

j186,6 (1 j1,73) ( 200 j100)( 1) (523 j86,6) ВА;

SEIUJ       



 

ИИ ИИ

Re 523 Вт;Im 86,6вар.PS QS 



Активная и реактивная мощности потребителей:



MCLL

QXIXIXIQ 2

1П

22 2

1 200 2 86,6 1,73 86,6 2( 100) 86,6 вар.      

Таким образом, баланс активных и реактивных мощностей вы-

полняется:

ИП И П

;.PP QQ

Примечание. Входящее в выражение реактивной мощности потре-

бителя слагаемое





 )argcos(arg22

IIXIIQ

212100cos(0 120) 200 вар   



представляет собой реактивную мощность, связанную с явлением вза-

имной индукции (о ней речь ниже).

Построение векторной диаграммы начинается с построения осей

комплексной плоскости (рис. 5.10) и выбора масштабов напряжения и

тока:

100 B дел.; 1 A дел.

mm

Затем строим лучевую диаграмму токов, проводя соответствующие

токам векторы из начала координат. Штриховыми линиями показаны

параллелограммы (в данном случае прямоугольники), иллюстрирующие

выполнение первого закона Кирхгофа. Для построения топографиче-

ской диаграммы напряжений подсчитаем комплексные потенциалы уз-

лов (в том числе устранимых). Узлов



нет на схеме. На диаграм-

ме они разделяют векторы напряжений само- и взаимоиндукции каждо-

го из элементов.

Пусть







Тогда

(50 j86,6) B;









( 50 j100) B; ( j ) ( 200 j100) B;

ba f b C

EIX

  

        



  

j120

j90 j60

1A; 1j 1,732 A;

j 1, 73 1, 73 A; 1 j 1, 73 2 A.

IIe

IeI e



 







222 1

(j )j

URXIXI  



j153,5

(50 j86,6) (-1+j1,73)+j100 1=-200+j100=223,6e B.  



22 22 22

П 1122 44

1 123 2 50 2 50 523 Вт;PIRIRIR 

22 22

( 50 j86,6) B; j 200 B;

nd f n L

RI XI

  



  



  

111

j ( 200 j100) B; 123 B;

ff M kd

XI IR

 



  



 

11 2

j (123 j200) B; j ( 50 j100) B.

bk L bb M

XI XI

 



    



 

Естественно, значения потенциалов узлов f и b, вычисленные раз-

личными способами, совпадают.



Теперь наносим точки a, b,



, d, f, , k, на комплексную плос-

кость и соединяем векторами так, чтобы они указывали своими стрел-

ками точки предполагаемого более высокого потенциала и чтобы их

взаимное положение на диаграмме соответствовало взаимному распо-

ложению элементов в схеме. Напряжения само- и взаимоиндукции по-

казаны пунктиром. Нетрудно видеть, что второй закон Кирхгофа также

выполняется.

5.5. Передача энергии между индуктивно

связанными элементами

Индуктивно связанные элементы имеют общее магнитное по-

ле, через которое и происходит передача энергии от одного эле-

мента к другому. Покажем это на примере схемы, изображенной на

рис. 5.11, в которой токи ориентированы одинаково по отношению

к одноименным зажимам элементов. Уравнения второго закона

Кирхгофа имеют вид:



111 2

222 1

jj;

jj,

UXIXI





 



где

11 2 2

e; e .II I I









Комплексные, активные и реактивные мощности элементов:

111 11 21 11 1

€

jj j j,

LM LMM

SUI X I X II Q P Q    



  

где

1211212

€

Re j sin( ),

MM M

PXIIXII











1211212

€

Im j cos( ).

QXIIII











222 2 12 22 2

€€

jj j j,

MLMM

SUI X I X II Q P Q    





где

21221121

€

Re j sin( ) .

MM M

PXIIXII P











21212211

€

Im j cos( ) .

MMM

Q X II II Q Q











Равенство

PP

говорит о передаче энергии от второго эле-

мента к первому, если





 

(при этом

P 

потребление

энергии,

P 

высвобождение энергии). Вместе же они могут

только накапливать энергию и возвращать ее источнику:

PP

Что касается реактивной мощности, то за счет наличия индуктивной

связи

LL M

QQ Q Q 

Очевидно, если изменить направление одного из токов, то изменят-

ся знаки активных и реактивных мощностей, связанных с явлением вза-

имной индукции.

Поэтому в общем случае

12 1 2

cos( ),

QXII





 

где знак

«плюс» соответствует одинаковой ориентации токов по отношению к

одноименным зажимам катушек, «минус» – противоположной. Добавку

нужно учитывать в реактивной мощности потребителей при со-

ставлении баланса мощностей, что и было сделано в примере 5.2. Пере-

дачу энергии между индуктивно связанными элементами позволяет ре-

ализовать трансформатор.

5.6. Эквивалентная замена индуктивно связанных элементов

(«развязка» индуктивной связи)

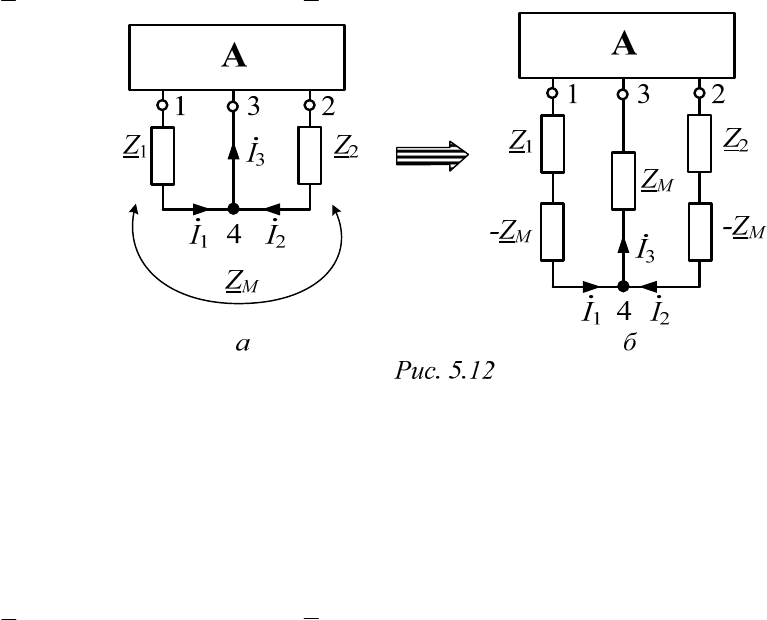
Рассмотрим схему, где от общего узла, к которому подключены

две ветви с индуктивно связанными элементами, отходит еще только

одна ветвь (рис. 5.12, а). По законам Кирхгофа

123 13 11 2 23 22 1

;j j;j j.

MLM

IIU XI XIU X I XI  

       

Отсюда

13 1 1 3 23 2 2 3

j( ) j ; j( ) j .

MM LM M

U XXIXIU X XIXI  

 

Легко увидеть, что последние формулы описывают и состояние

схемы рис. 5.12, б (без индуктивной связи), следовательно, эти схемы

эквивалентны. Обратим внимание, что изменение направления одного

из токов (например,



) не приводит к изменению параметров эквива-

лентной схемы. Меняется лишь знак перед



во всех уравнениях.

Правило развязки в данном случае можно сформулировать так:

если индуктивно связанные элементы подключены к общему узлу

одноименными зажимами, то в эквивалентной схеме без индуктивной

связи последовательно с каждым из них включается сопротивление



, а в третью ветвь





Аналогично доказывается переход от схемы рис. 5.13, а с индук-

тивной связью к схеме рис. 5.13, б без нее.

Правило развязки на этот случай:

если индуктивно связанные элементы подключены к общему узлу

разноименными зажимами, то в эквивалентной схеме без индуктивной

связи последовательно с каждым из них включается сопротивление



, а в третью ветвь .





Напоминаем, что способ включения катушек (согласное или

встречное) на результат развязки не влияет!

Если от общего узла, кроме ветвей с индуктивной связью, отходит

две или большее количество ветвей, то, прежде чем производить развяз-

ку, схему следует так перерисовать, чтобы привести к одному из выше-

рассмотренных случаев.

Например, перечертив часть схемы

рис. 5.9 вблизи узла d, расщеп-

ленного на

(рис. 5.14, а), так, как показано на рис. 5.14, б, мо-

жем заменить ее эквивалентной (рис. 5.14, в). А уже эквивалентную

схему без индуктивной связи в дальнейшем можно рассчитать и мето-

дом узловых потенциалов, и методом эквивалентного генератора, и ме-

тодом преобразований.









5.7. Двухобмоточный трансформатор в линейном режиме

Трансформатор представляет собой устройство, предназначенное

для преобразования электрической энергии одного напряжения и тока в

энергию другого тока и напряжения. Эта энергия передается из одной

части цепи в другую за счет явления взаимной индукции.

Обычно трансформатор состоит из двух или нескольких обмоток.

Чтобы увеличить коэффициент связи, обмотки помещают на ферромаг-

нитный сердечник

. Если сердечник ненасыщен, то его вебер-амперная

характеристика линейна. Для работы в схемах с высокочастотными ис-

точниками используются трансформаторы без ферромагнитного сер-

дечника (так называемые воздушные трансформаторы – тоже линейные

устройства).

Рассмотрим двухобмоточный трансформатор в линейном режиме.

Одна из его обмоток, называемая первичной (индекс 1), подключается к

источнику, другая – вторичная обмотка (индекс 2) –

подключается к при-

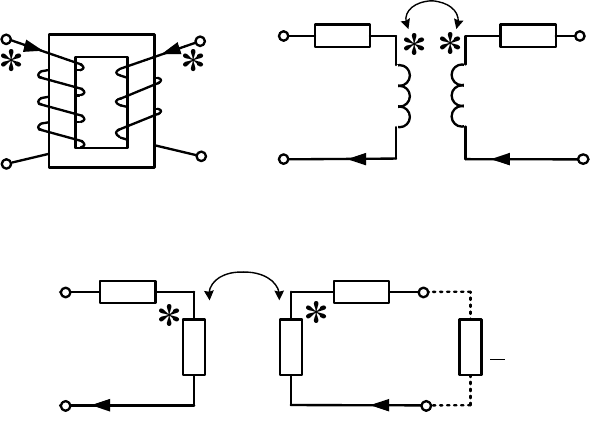
емнику. Обмотки можно подключить и наоборот. На рис. 5.15 показаны

его принципиальная схема (а) и схема замещения (б), а на рис. 5.16 –

комплексная схема замещения трансформатора с индуктивной связью.

а б

Рис. 5.15

Рис. 5.16

Если в режиме холостого хода напряжение на зажимах вторичной

обмотки больше напряжения на входе трансформатора, то он называет-

ся повышающим, в противном случае – понижающим. Фактически каж-

дый трансформатор в зависимости от способа включения может слу-

жить как повышающим, так и понижающим. Отношение напряжения на

зажимах обмотки высшего напряжения к напряжению

на зажимах об-

мотки низшего напряжения в режиме холостого хода трансформатора

принято называть коэффициентом трансформации: