Ензельт Ольга. Уроки математики в 5 класі. Конспекти уроків
Подождите немного. Документ загружается.


220
4)
1010,6 326
978 3,1 (год)
326
326
0
–
–
— час проти течії;
5) 2,6 + 3,1 = 5,7 (
год).
Відповідь. Човен пропливе увесь шлях за 5,7 годин.
№963 (5–9).
Учні складають план розв’язання кожного рівняння.
III. Підсумки уроку. Пояснення домашнього завдання.
№№958 (2), 970, 964 (4–6).
УРОК 109. РОЗВ’ЯЗУВАННЯ ТЕКСТОВИХ ЗАДАЧ
Мета. Повторити алгоритм розв’язування задач на знаходження дробу від числа та
поширити цей алгоритм на випадок, якщо дріб десятковий; формувати навич-
ки розв’язування задач на застосування зазначеного алгоритму.
Тип уроку. Урок засвоєння нових знань.
Хід уроку
I. Перевірка домашнього завдання.
№958 (2).
Учні називають послідовність виконання дій та результат кожної дії.
№970.
Учитель задає запитання, а учні відповідають на них.
1.
Яку відстань проскакав перший вершник до зустрічі?
2.
Яку відстань проскакав другий вершник?
3.
Як знайти швидкість другого вершника?
№964.
Учні повідомляють план розв’язування рівняння та його корінь.
II. Актуалізація опорних знань.
1. На що вказує знаменник дробу? чисельник дробу?
2. Розв’яжіть усно задачі:
1) Скільки градусів становить:
а)
1
2
прямого кута;
221
б)
1
10
прямого кута;
в)
1
30
розгорнутого кута?
2) Учні зібрали 16 кг насіння лісових дерев,
1
4
яких становили жолуді.
Скільки жолудів зібрали учні?
III. Сприймання і засвоєння навчального матеріалу.
№949.
1) Як записати 0,1 у вигляді звичайного дробу?
2)
На що вказує знаменник дробу?
3)
Скільки гривень заплатив Василько за книжку?
12
грн
.
?
0,1 =
1
10
.
12 : 10 = 1,2 (грн.) — припадає на
1
10
частину;
Відповідь. Василько заплатив за книжку 1,2 грн.
IV. Закріплення вивченого матеріалу.
№951.
1) Як записати 0,6 у вигляді звичайного дробу?
2)
На що вказує знаменник дробу?
0,6 =
6
10
.
180
с
.
?
180 : 10 ⋅ 6 = 108 (
с.).
Відповідь. Петрик прочитав 108 сторінок.

222
№982.
І — ?, 0,4 від
ІІ — ?, 0,35 від решти
ІІІ —
1234
грн
.
1) 0,4 =
4
10
; 1234 : 10 ⋅ 4 = 493,6 (грн.) — за I місяць;
2) 1234 – 493,6 = 740,4 (
грн.) — решта;
3) 0,35 =
35
100
; 740,4 : 100 ⋅ 35 = 259,14 (грн.) — за II місяць.
Відповідь. За другий місяць було витрачено 259,14 гривень.
№963 (10–12).
№979.
V. Підсумки уроку. Пояснення домашнього завдання.
№№950, 952, 983.
УРОК 110. РОЗВ’ЯЗУВАННЯ ТЕКСТОВИХ ЗАДАЧ
Мета. Повторити алгоритм розв’язування задач на знаходження числа за його дро-
бом та поширити цей алгоритм на випадок, якщо дріб десятковий; формувати
навички розв’язування задач на застосування зазначеного алгоритму.
Тип уроку. Урок засвоєння нових знань.
Хід уроку
I. Перевірка домашнього завдання.
Учні усно по черзі повідомляють хід розв’язування задач, решта звіря-
ють відповіді у своїх зошитах.
II. Актуалізація опорних знань.
Розв’яжіть усно задачі:
1. У класі є 5 відмінників, що становить
1
6
всіх учнів класу. Скільки учнів
у класі?
2. Морквою засіяли 35 га, що становить
5
8
усієї площі поля. Визначте
площу всього поля.
223
III. Сприймання і засвоєння навчального матеріалу.
№953.
1) Як записати 0,1 у вигляді звичайного дробу?
2)
Скільки кілометрів припадає на десяту частину маршруту?
3)
Яка довжина всього маршруту?
0,1 =
1
10
.
2,7
?
2,7 ⋅ 10 = 27 (
км).
Відповідь. Довжина маршруту становить 27 км.
IV. Закріплення вивченого матеріалу.
№955.
1) Як записати 0,6 у вигляді звичайного дробу?
2)
Скільки дерев припадає на одну десяту частину?
3)
Скільки дерев росте в парку?
0,6 =
6
10
;
48 : 6 ⋅ 10 = 80 (
д.).
Відповідь. Усього в парку росте 80 дерев.
№984.
1) Як записати 0,36 у вигляді звичайного дробу?
0,36 =
36
100
.
2)
Скільки припадає на одну соту частину суми?
2,88 36
288 0,08
0
–
3)
Чому дорівнює сума?
0,08 ⋅ 100 = 8.
4)
Як знайти другий доданок?
8 – 2,88 = 5,12.
Відповідь. Другий доданок дорівнює 5,12.

224
№986.
1) Знайдемо 0,68 числа 50.
0,68 =
68
100
;
50 : 100 ⋅ 68 = 34.
2)
Знайдемо число 0,85 якого дорівнює 34.
0,85 =
85
100
;
34 : 85 ⋅ 100 = 40.
Відповідь. 40 — шукане число.
№989.
Якщо хлопчик прочитав 0,35, а потім ще 0,1 книжки, то всього він про-
читав 0,35 + 0,1 = 0,45 книжки. Половина книжки — це
1
2
, або 0,5 книжки,
тобто 0,45 книжки менше від 0,5 книжки на 0,5 – 0,45 = 0,05, що становить
15
сторінок.
Отже, 0,05 =
5
100
книжки становить 15 сторінок, а вся книжка —
15 : 5 ⋅ 100 = 300
сторінок.
Відповідь. 300 сторінок.
V. Підсумки уроку. Пояснення домашнього завдання.
№№954, 956, 987.
УРОК 111. РОЗВ’ЯЗУВАННЯ ТЕКСТОВИХ ЗАДАЧ
Мета. Закріпити навички розв’язування задач і вправ на множення та ділення десят-
кових дробів; розвивати активність і увагу учнів.
Тип уроку. Урок узагальнення і систематизації знань.
Хід уроку
I. Перевірка домашнього завдання.
Учитель завчасно записує на дошці правильні відповіді до домашнього
завдання. Кожен учень звіряє їх. Якщо виникають запитання, то вчитель від-
повідає на них.
225
II. Формування умінь і навичок.
Розв’язування задач і вправ. Колективна робота
Додатково:
№1.
Селянська спілка «Поділля» має 120 га поля. Картоплею засаджено
0,4
поля, а решту — засіяно пшеницею. Скільки гектарів засаджено картоп-
лею і скільки гектарів засіяно пшеницею?
картопля пшениця
120
1) 120 : 10 ⋅ 4 = 48 (
га) — засаджено картоплею;
2) 120 – 48 = 72 (
га) — засіяно пшеницею.
Відповідь. 48 га, 72 га.
№2.
У трьох гаражах є 360 машин. У першому гаражі — 120 машин, у дру-
гому — 0,9 тієї кількості, що в першому, а решта — в третьому. Скільки ав-
томашин в другому і третьому гаражах окремо?
1) 120 : 10 ⋅ 9 = 108 (
м.) — машин у другому гаражі;
2) 360 – (120 + 108) = 132 (
м.) — машин у третьому гаражі.
Відповідь. 108 м; 132 м.
№3.
Довжина поля прямокутної форми дорівнює 1,6 км, а ширина становить
0,25
довжини. Скільки потрібно насіння, щоб засіяти це поле, якщо на 1 га
висівають 1,6 ц насіння?
1) 1,6 : 100 ⋅ 25 = 0,4 (
км) — ширина поля;
2) 1,6 ⋅ 0,4 = 0,64 (
км
2
) — площа поля;
0,64
км
2
= 640000 м
2
= 64 га;
3) 64 ⋅ 1,6 = 102,4 (
ц) — насіння.
Відповідь. 102, 4 ц насіння.
№4.
Фермер засіяв горохом поле прямокутної форми. Довжина поля дорів-
нює 1,25 км, а ширина становить 0,28 довжини. Скільки центнерів гороху зі-
брав фермер з цього поля, якщо з кожного гектара він збирав по 25 ц?
1) 1,25 : 100 ⋅ 28 = 0,35 (
км) — ширина поля;
2) 1,25 ⋅ 0,35 = 0,4375 (
км
2
) — площа поля;
0,4375
км
2
= 437500 м
2
= 43,75 га;

226
3) 43,75 ⋅ 25 = 1093,75 (ц) — гороху.
Відповідь. 1093,75 ц гороху.
№5.
Риба при в’яленні втрачає 0,48 своєї початкової маси. Скільки потрібно
свіжої риби, щоб мати 115,7 т в’яленої?
Маса риби після в’ялення становить 1 – 0,48 = 0,52 частин від маси сві-
жої риби. Оскільки 0,52 становить 115,7, то 0,01 становить 115,7 : 52 = 2,225.
2,225 ⋅ 100 = 222,5 (
т).
Відповідь. Потрібно 222,5 т риби.
№6.
Буряки при переробці їх на цукор втрачають 0,85 своєї початкової маси.
Скільки потрібно взяти буряків, щоб мати 360 кг цукру?
Маса цукру становить 1 – 0,85 = 0,15 частин початкової маси буряків.
360 : 15 ⋅ 100 = 2400 (
кг).
Відповідь. 2400 кг буряків.
III. Підсумки уроку. Пояснення домашнього завдання.
№№985, 1098.
УРОК 112. СЕРЕДНЄ АРИФМЕТИЧНЕ. СЕРЕДНІ ВЕЛИЧИНИ
Мета. Формувати вміння знаходити середнє арифметичне і розв’язувати вправи на
застосування цього поняття.
Тип уроку. Урок засвоєння нових знань.
Хід уроку
I. Актуалізація опорних знань.
1. Подвойте суму 1,4 + 18,7 + 6,3 + 3,6.
2. Знайдіть четверту частину різниці 5,2 – 2,5.
3. Знайдіть п’яту частину добутку 1,8 ⋅ 1,5.
II. Мотивація навчання.
Ми часто чуємо слово «середній». Середня заробітна плата у промисло-
вості, середньодобова температура, середній урожай з 1 га, середній надій
молока на одну корову. З’ясуємо його зміст.
III. Сприймання і засвоєння навчального матеріалу.
Задача 1. Шкільна бригада за перший день прополола 4,2 а буряків, а за
другий день — 3,9 а, а за третій — 4,5 а. Визначте середній виробіток брига-
ди за день.

227
1) Знайдемо, яку площу прополола шкільна бригада за три дні.
4,2 + 3,9 + 4,5 = 12,6 (
а).
2)
Середній виробіток показує, скільки гектарів прополола бригада за
1
день, якщо вважати, що кожного дня вона прополювала однакову площу.
12,6 : 3 = 4,2 (
а).
Задача 2. Туристи за першу годину пройшли 2,6 км, за другу — 3,3 км,
а за третю — 2,5 км. З якою сталою швидкістю потрібно було б їм іти, щоб
подолати всю відстань за такий же час.
v
с
=
2,6 3,3 2,5
3
++
=
8,4
3
= 8,4 : 3 = 2,8 (км/год).
Для розв’язання задачі ми знайшли суму 3-х доданків і поділили їх на 3
(
кількість доданків).
Середнім арифметичним кількох чисел називають частку від ділення
суми цих чисел на кількість доданків.
IV. Закріплення вивченого матеріалу.
№997.
Учні розв’язують, коментуючи правило знаходження середнього ариф-
метичного.
№998.
№1003.
Для розв’язування цієї задачі учні складають рівняння:
7,8
2
x
+
= 7,2;
7,8 +
x = 7,2 ⋅ 2;
7,8 +
x = 14,4;
x = 14,4 – 7,8;
x = 6,6.
Відповідь. 6,6.
№1005.
Для розв’язування цієї задачі учні складають рівняння.
Нехай одне число x, тоді друге — 4x. Середнє арифметичне цих чисел
дорівнює
4
2
xx
+
, що за умовою задачі дорівнює 10.
4
2
xx
+
= 10;
x + 4x = 20;
5
x = 20;
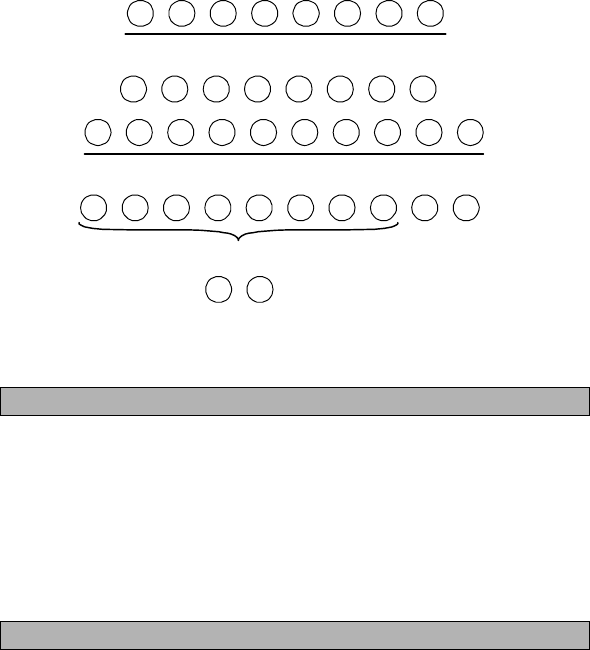
228
x = 4.
Отже, перше число дорівнює 4, а друге 4 ⋅ 4 = 16.
№1007.
Для розуміння розв’язку цієї задачі запишемо схему.
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8
8
= 7
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8
= 56
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
10
= 8
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
56
= 80
9 + 10
= 80 – 56 = 24
За кожну з двох останніх задач Дмитрик має отримати 24 : 2 = 12 балів.
№1015 (1).
V. Підсумки уроку. Пояснення домашнього завдання.
§5, п. 33, №№1000, 1004, 1015 (2).
УРОК 113. СЕРЕДНЄ АРИФМЕТИЧНЕ. СЕРЕДНІ ВЕЛИЧИНИ
Мета. Закріпити знання про середнє арифметичне чисел; формувати поняття серед-
ньої величини (швидкості, ціни) та вміння розв’язувати відповідні задачі.
Тип уроку. Урок формування умінь і навичок.
Хід уроку
I. Актуалізація опорних знань.
Завдання завчасно записані на дошці.
1. Знайдіть середнє арифметичне чисел:
а) 8,1 і 8,3; б) 1,2; 1,3 і 1,4; в) 0,4; 0,6; 0,7 і 1,5.
2. Розв’яжіть рівняння:
а) 2,7 + a = 5,3; б) 1,64c + 1,36c = 4,8;
в) b – 0,4 = 3,6; г) 8d – 0,8d = 720.

229
II. Формування умінь і навичок.
На попередньому уроці ми розглянули приклади так знаних «середніх
значень» (середня температура повітря за місяць, середня кількість опадів,
середня заробітна плата).
Також ми розглянули особливий випадок середніх величин, середнє
арифметичне кількох чисел.
Чи можна застосувати поняття середнього арифметичного для знахо-
дження середніх величин? Розглянемо приклад 1 (підручник, п. 33).
Ми знаємо, що взагалі v =
S
t
, де v — швидкість руху, S — шлях, t —
час руху, тому для знаходження шуканої швидкості знайдемо увесь шлях, по-
тім загальний час руху і поділимо знайдене значення шляху на загальний час.
1) 54 ⋅ 4 + 60 ⋅ 2 = 216 + 120 = 336 (
км) — увесь шлях;
2) 4 + 2 = 6 (
год) — загальний час руху;
3) 336 : 6 = 56 (
км/год) — середня швидкість руху.
Чи можна було розв’язати задачу, знайшовши середнє арифметичне
значень швидкостей?
Перевіримо:
54 60 114
57
22
+
==
.
Отримали іншу відповідь. Отже, серед-
нє арифметичне швидкостей на різних ділянках шляху не є значенням серед-
ньої швидкості руху.
Отже, щоб знайти середню швидкість руху, потрібно весь пройдений
шлях поділити на загальний час руху.
Розглянемо приклад 2 (п. 33) за підручником.
У цій задачі йдеться про середнє значення ціни. Зрозуміло, що середня
ціна покупки дорівнює вартості покупки, поділеній на кількість одиниць то-
вару (штук, кілограмів), тому, щоб знайти вартість покупки, потрібно серед-
ню ціну помножити на кількість кілограмів усього купленого печива.
1) 2,4 + 3,2 = 5,6 (
кг) — загальна маса печива;
2) 14 ⋅ 5,6 = 78,4 (
грн.) — загальна вартість покупки;
3) 10,2 ⋅ 2,4 = 24,48 (
грн.) — коштує печиво першого виду;
4) 78,4 – 24,48 = 53,92 (
грн.) — коштувало печиво другого виду;
5) 53,92 : 3,2 = 16,85 (
грн.) — ціна 1 кг печива другого виду.
Перевірмо, чи можна було б отримати цю відповідь, використавши по-
няття середнє арифметичне: якщо x (грн.) ціна печива другого виду, то сере-
днє арифметичне ціни:
10,2
14
2
x+
= ;
10,2 +
x = 28;
x = 28 – 10,2 = 17,8.
