Емельянов В.Ю. Методы моделирования стохастических систем управления

Подождите немного. Документ загружается.

143

ская характеристика такого звена будет иметь вид (u)=F

-1

(u). В зависимо-

сти от вида (u) безынерционная нелинейность может изменить корреляци-

онную функцию преобразуемого сигнала.

В свою очередь, формирующий фильтр, представляющий собой линей-

ное динамическое звено, видоизменяет не только спектральную плотность и

корреляционную функцию, но и закон распределения формируемого сигна-

ла. При достаточно высоком порядке знаменателя передаточной функции

формирующий фильтр нормализует закон распределения преобразуемого

сигнала. Для компенсации такого побочного эффекта обычно рекомендуется

на первом этапе обеспечить заданные корреляционные свойства модели-

руемого процесса с помощью формирующего фильтра или скользящего

суммирования, после чего, вычислив математическое ожидание m

и сред-

неквадратическое отклонение 

полученного процесса, выполнить допол-

нительное нелинейное преобразование сигнала вида

   

 













dveuФu

. (4.51)

Считается, что после этого в соответствии с (3.25) будет восстановлен

исходный равномерный в интервале [0; 1] закон распределения значений

процесса. Затем можно проводить формирование заданного закона распре-

деления.

Однако при практической реализации генератора случайного процесса

указанные теоретические результаты, как правило, не подтверждаются. Это

связано, во-первых, с невысоким качеством стандартных генераторов равно-

мерно распределенных случайных чисел, используемых в распространенных

программных средствах, применяемых при реализации моделей на ЦВМ. Во-

вторых, все теоретические результаты, на которых основан метод статистиче-

ского моделирования, при конечных объемах выборок, получаемых на прак-

тике, имеют заведомо ограниченную достоверность.

Вследствие этого закон распределения псевдослучайной последователь-

ности

 ,...,,

, получаемой со стандартного генератора, в большей или

меньшей степени отличается от равномерного, а корреляционная функция

получаемого на его основе "белого шума" - отличается от -функции. Кроме

того, взаимное влияние рассмотренных этапов преобразования пр оцесса

оказывается более существенным и в общем случае непредсказуемым.

Таким образом, точное воспроизведение заданных характеристик слу-

чайного процесса является сложной задачей, требующей выполнения не-

144

скольких этапов преобразований, контроля получаемых результатов после

каждого этапа на основе вычисления оценок (3.11)-(3.12), восстановления

законов распределения и применения критериев согласия, а также немалой

изобретательности. Большое число полезных практический рекомендаций

содержится в монографии [47].

4.10. Пример статистической имитационной модели системы

со случайными параметрами при действии случайной помехи

Рассмотрим модель системы, описанной в подразд. 3.8, учитывая до-

полнительно воздействие на канал измерения угловой координаты цели шу-

мовой помехи. Примем, что эффект воздействия помехи сводится к появле-

нию случайной ошибки измерения угла наклона линии визирования:



= 

+ (t) для состояния x



= 

эцо

+ (t) для состояния x



= 

лц

+ (t) для состояния x

Случайный стационарный процесс (t) имеет нормальный закон рас-

пределения с математическим ожиданием m



и дисперсией D



и корреляци-

онную функцию:



()=D



-||

При реализации статистической имитационной модели на ЦВМ нео бхо-

димо будет формировать значения (t) на каждом шаге интегрирования

дифференциальных уравнений модели.

Будем использовать стандартный генератор случайных чисел, распреде-

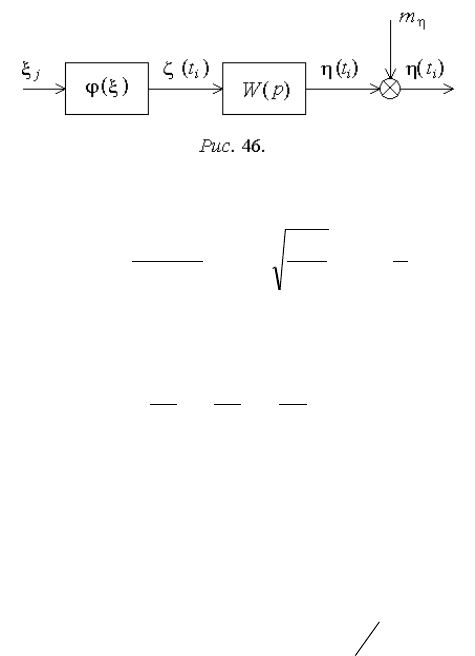
ленных в интервале [0; 1] по равномерному закону. Процедура формир ова-

ния реализаций процесса (t) схематично показана на рис. 46, где () -

преобразование равномерно распределенной последовательности псевдо-

случайных чисел в реализацию белого шума со стандартизованным нор-

мальным распределением:

 





j

145

в результате чего получаем: m



=0, D



=1; W(p) - передаточная функция

формирующего фильтра

 

1+pT

pW 







где h - шаг интегрирования модели.

Формирующий фильтр реализуем добавлением в систему уравнений

(3.27) дополнительного уравнения





Tdt

d 1

которое должно интегрироваться совместно с остальными уравнениями

модели, и начального условия (0)=m



. Значения  для каждого шага интег-

рирования формируются путем 12-кратного обращения к генератору слу-

чайных чисел и использования преобразования ().

Отметим, что вычислительная трудоемкость модели существенно повы-

сится по сравнению с рассмотренным выше ее вариантом. Теперь для полу-

чения каждой реализации моделируемого процесса, помимо дополнитель-

ных арифметических операций потребуется еще

T12

обращений к генера-

тору случайных чисел (T - продолжительность моделируемого процесса).

Кроме того, для такой модели оказывается недопустимым использование

итерационных методов интегрирования с автоматическим выбором шага.

5. СПОСОБЫ СНИЖЕНИЯ ТРУДОЕМКОСТИ

СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ

5.1. Основные методы уменьшения дисперсии оценки

146

Как видно из представленных в подразд. 3.3 соотношений, уменьшение

дисперсии используемой при статистическом моделировании оценки иско-

мой характеристики позволит пропорционально снизить количество опытов,

необходимых для получения результата с заданной точностью.

Рассмотрим наиболее известные методы уменьшения дисперсии оцен-

ки на примере задачи определения математического ожидания некоторого

показателя качества динамической системы со случайными параметрами.

Модель динамической системы задается в виде системы уравнений

    

VttXtX

,,



, i=1,2,...,n, (5.1)

где X(t)=(X

(t),X

(t),…,X

(t)) - вектор переменных состояния системы;

V=(V

,…,V

) - вектор случайных параметров. Качество системы харак-

теризуется мгновенным значением переменной состояния X

в момент вре-

мени t

. Таким образом, задача сводится к оценке математического ожида-

ния m

=M[X

(t,V)].

При использовании стандартной схемы статистического моделирования

оценка m

для заданной m-мерной ПРВ вектора случайных параметров f

(V)

определяется по формуле (3.2), а необходимое для обеспечения заданной

точности количество опытов - по формуле (3.19).

5.1.1. Метод выделения главной части

Решение системы (5.1) X

(t,V), которое, возможно, не может быть най-

дено аналитически, заменяют приближенным выражением Y(t,V), удобным

для аналитических преобразований. Например:

     



 



kjjk

VVtbVtatatY

1 11

),( V

или для единственного случайного параметра

       

VtaVtataVtY  

где a

(t),b

(t) - некоторые функции времени.

Вводится новая переменная состояния Z(t,V)=X

(t,V)-Y(t,V) и в сис-

теме уравнений (5.1) выполняется замена переменной X

на Z путем подста-

новки:

         



 



kjjk

VVtbVtatatZtX

1 11

,, VV

147

         



 





kjjk

VVtbVtatatZtX

1 11

,, VV

или

         

VtaVtataVtZVtX  

101

         

VtaVtataVtZVtX



 

101

Оценка искомого математического ожидания определяется в виде:

=M[Y(t

,V)]+M[Z(t

,V)],

где первое слагаемое может быть найдено аналитически:

 

 

   





dvdvftYtYM ...,,

111

VVV 

G - область возможных значений вектора V, а второе слагаемое определяется

по методу статистического моделирования на основе многократного реше-

ния полученной новой системы уравнений до момента времени t





tZM

)],([ V

 

tZz



, V

(i)

- i-я реализация вектора случай-

ных параметров, N - количество решений системы уравнений для различных

(i)

При удачном выборе функции Y(t,V) дисперсия случайной величины

Z(t

,V) может оказаться существенно меньше, чем дисперсия X

,V), что

и приведет к сокращению требуемого количества опытов.

Пример. Рассмотрим достаточно простой пример, все необходимые

расчеты для которого могут быть выполнены точно на основе аналитич еских

решений. Пусть требуется определить математическое ожидание выходного

сигнала X апериодического звена 1-го порядка через 1с после подачи на вход

сигнала 1(t). Коэффициент передачи звена k=4. Постоянная времени и на-

чальное значение выходного сигнала - случайные:

T 

, X(0)=V

. Па-

раметр V

распределен по равномерному закону в интервале [0; 1] , пара-

метр V

- по равномерному закону в интервале [1; 2] , V

и V

статистиче-

ски независимы. Допустимая абсолютная погрешность результата 

доп

0,01.

148

Искомое математическое ожидание m

=M[X(1)], дисперсия D[X(1)] и

необходимое количество опытов могут быть оценены на основе статистиче-

ского моделировани или определены аналитически.

Сначала получим точное решение задачи. Изменение сигнала X во вре-

мени описывается дифференциальным уравнением

kXXT 



. (5.2)

Решение (5.2) имеет вид:

   

kekVtX





Для t=1 с учетом статистической независимости параметров V

и V

получим:

 

   







kdvekdvedvvkekMeMVMm

vvVV

222

1111

   

419,241415,1

 



eekkee

 

 

 

 





















111

VVV

eMVkMeMVMkekVMXM

 

   

0954,6

111

2 



 keMkeMVkMeMk

VVV

 

 

 

 

2438,0

1 

mXMXD 1

С учетом известной D[X(1)] по (3.19) оценим количество опытов, необ-

ходимое для оценки m

методом статистического моделирования с погреш-

ностью, не превышающей 

доп

(при доверительной вероятности 0,997):

 

 

21942







доп

треб

При решении этой же задачи методом статистического моделирования

на основе итерационного алгоритма (с. 65) получены следующие оценки

(БЭЙСИК, IBM PC, объем начальной серии опытов n

=500):

416,2



 

 

2391,01 



 

21517





треб

В процессе решения фактически выполнено

 

21906

N

опытов.

Применим теперь к этой задаче метод выделения главной части. При-

ближенное решение уравнения (5.2) выберем в виде

Y(t,V)=(V

-k)(1-V

t)+k. (5.3)

Его математическое ожидание при t=1 легко вычисляется аналитически:

149

M[Y(1)]=(M[V

] - k)(1-M[V

] )+k = (1,5-4)(1-0,5)+4=2,750.

Выполним в уравнении (5.2) замену переменной:

X=Z+V

+kV

t-V

211

VVkVZX 



Получим новое уравнение

 

tkVVZZT 



, аналитическое реше-

ние которого имеет вид:

       

kVtVkVekVtZ





2122

Для t=1 интегрированием аналитического решения получим:

M[Z(1)] = - 0,331, D[Z(1)] = 0,0796,

 

7164



треб

Таким образом, представляется возможным для рассматриваемой за-

дачи путем выделения главной части в виде (5.3) сократить трудоемкость

статистического моделирования в

 

7164

21942



треб

раза.

При контрольном статистическом моделировании на основе исполь-

зованного выше алгоритма получены следующие оценки:

323,0)]1([ 



427,2



0792,0)]1([ 



 

7125





треб

В процессе решения фактически выполнено

 

7143

N

опыта. На

практике трудоемкость моделирования сокращена в

 

07,3

7143

21906



раза.

Выберем другой вариант приближенного решения уравнения (5.2)

   

kVtY 















Для него получим:

M[Y(1)]=2,125,

211

tVVtkV

VZX 

211

VVkV

ZX 



 

tkV

ZZT







150

   

 

kVtV

ekVtZ





 



На основе аналитического решения для t=1: M[Z(1)]=0,294,

D[Z(1)]=0,0124,

 

1113



треб

- и ожидаемый выигрыш в количестве опытов

1113

21942



раз.

При контрольном статистическом моделировании здесь были получены

следующие оценки:

298,0)]1([ 



423,2



0116,)]1([ 0



 

1045





треб

, фактическое количество опытов

 

1046

N

и выигрыш в

трудоемкости в

9,20

1046

21906



раза.

5.1.2. Метод существенной выборки

Преобразуем общее соотношение для определения математического

ожидания m

=M[X

,V)] по генеральной совокупности следующим об-

разом:

   

 

   





dvdvpf

dvdvftXm ...

...,

111

VV 

   





dvdvftY ...,

VV

. (5.4)

Из соотношения (5.4) следует, что искомое математическое ожидание

совпадает с математическим ожиданием новой функции

 



, для которой вектор случайных параметров V имеет

плотность распределения вероятностей

 

VVV pff

)()(



. Это матема-

тическое ожидание может быть определено на основе статистического моде-

лирования:

 

 

 









tYMm

. (5.5)

Причем при удачном выборе функции p(V) дисперсия оценки (5.5) может

оказаться существенно ниже, чем дисперсия оценки m

по (3.2).

151

Функция p может иметь в качестве аргументов только часть случайных

параметров задачи. В любом случае она должна удовлетворять условию:

   

1...





dvdvpf VV

. (5.6)

Для достижения наибольшего эффекта функцию p(V) следует выбирать

приблизительно пропорциональной X

,V)f

(V) [17].

Пример. Выберем для рассмотренного выше примера функцию p в виде

   

 















1или0при

10при

5,24

Vpp

(5.7)

Из условия (5.6) найдем коэффициент a:

 

153

5,24







 e

dvea

 





Задача оценки m

сводится к оценке математического ожидания новой

случайной функции

   

 

5,242

153

),,1()1(

VVYY







где X(1) - решение уравнения (5.2) при t=1, параметр V

должен иметь рас-

пределение (5.7), а параметр V

- исходное распределение, равномерное в

интервале [1; 2].

Точное значение дисперсии функции Y(1) может быть найдено сле-

дующим образом:

 

 

 

 

 

 

 

 

1111

mYMYMYMYD 

 

 

  

 

 





 



5,242

1 dvdv

kekv

. (5.8)

Значение интеграла (5.8) может быть получено только численным ин-

тегрированием и составляет

8968,5)]1([

YM

. В результате D[Y(1)]=0,0452,

требуемое количество опытов для оценки M[Y(1)] на основе статистического

моделирования с заданной точностью

 

4071



треб

и ожидаемый выигрыш

в трудоемкости - в

4,5

4071

21942



раза. Отметим, что закон распределения

(5.7) не поддается воспроизведению по методу обратных функций. Следова-

тельно, генератор для случайного параметра V

придется строить, например,

152

по методу Неймана, и в результате выигрыш в общей трудоемкости решения

задачи окажется несколько ниже.

При контрольном статистическом моделировании с использованием ге-

нератора, построенного по методу Неймана, здесь были получены следую-

щие оценки:

419,2)]1([ 



YMm

0433,0)]1([ 



 

3895





треб

фактическое количество опытов

 

4849

N

при 6194 обращениях к генера-

тору случайных чисел и выигрыш в трудоемкости в 4,2 раза.

Для сравнения отметим, что при выборе

 



















,илипри

,при

)()(

Vpp V

аналогичном успешно использованному выше выбору главной части, полу-

чим D[Y(1)]=0,8932, и рассмотренный метод дает значительный отрицатель-

ный эффект.

5.1.3. Метод расслоенной выборки (выборка по группам)

В соответствии с данным методом область G возможных значений слу-

чайного вектора разбивается на K непересекающихся областей G

GGGG 



. Метод предполагает проведение статистического

моделирования для каждой из областей G

с использованием для вектора

случайных параметров плотностей распределения вероятностей

 

V 

, (5.9)

где p

- вероятность попадания случайного вектора V в область G

 





dvdvfp

...

V

Если для области G

выполним N

опытов, получим оценку математи-

ческого ожидания искомого показателя для данной области:

   

 









Результирующая оценка



должна рассматриваться как дискретная

случайная величина, значения которой

 



наблюдаются с вероятностями

. Тогда результирующая оценка определяется усреднением: