Емельянов В.Ю. Методы моделирования стохастических систем управления
Подождите немного. Документ загружается.


93
рода необходимо, помимо основной, ввести противоречащую ей альтерна-
тивную (конкурирующую) параметрическую гипотезу G, например: >
0
,
<
0
или
0
. Тогда вероятность ошибки второго рода определяется
следующим образом: P(W
д
G). Здесь, в отличие от (3.31), закон
распределения W определяется при условии выполнения гипотезы G. Веро-
ятность недопущения ошибки второго рода 1-называется мощностью
статистического критерия.
В общем случае выбирать статистический критерий для конкретной за-
дачи и строить запретную область следует таким образом, чтобы обеспечить
максимум вероятности Однако на практике в большинстве случаев здесь
применяют готовые рецепты. Тогда заданное значение или используется
для определения необходимого объема выборки.
Пример: проверка гипотезы о значении математического ожидания
случайной величины с нормальным законом распределения и известной
дисперсией.
Основная гипотеза H: m
x
=.
Конкурирующая гипотеза G: m
x
.
Статистический критерий:
x
x
m
n
W
, (3.32)
где n - объем выборки;
x
- известное среднеквадратическое отклонение; m
*
x
- оценка математического ожидания, определяемая на основе (3.2). Закон
распределения W нормальный, причем
W
=1, а
x
x
W
m
n
m
. При
выполнении гипотезы H получим m
W
=0 (стандартизованный нормальный
закон).
Допустимая область для критерия W строится в виде интервала
[w
л
;w
п
], причем при заданном уровне значимости условие (3.31) примет
вид:
P(W<w
л
H)+P(W>w
п
H)=.
Для однозначного определения границ интервала принимается допо л-
нительное условие: P(W<w
л
H)=P(W>w
п
H)=0,5. Тогда с учетом
m
W
=0 допустимая область будет иметь вид [-w
0,5
;w
0,5
]. Значение w
0,5
может быть найдено по таблицам нормального закона распределения*. Те-
перь по имеющейся выборке находят оценку математического ожидания и
-------------------
Рекомендуется самостоятельно рассмотреть числовые примеры, выбрав зна-
чения =1-P
д
в соответствии с табл. 7, и сравнить получаемые значения w
0,5
и
д
.
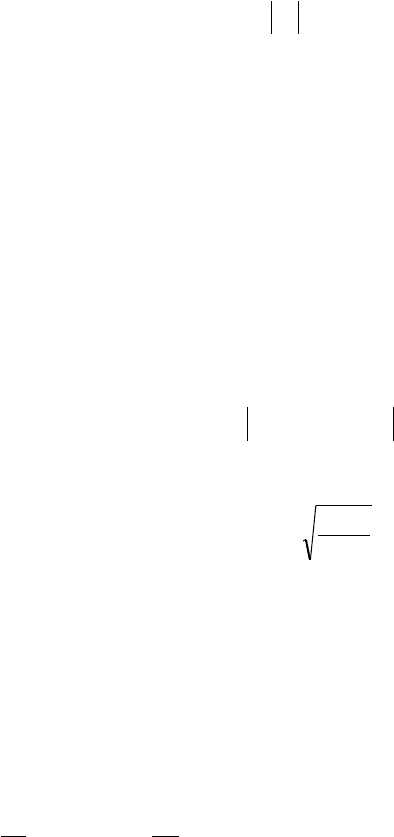
94
определяют по (3.32) расчетное значение статистического критерия w
*
. Ос-
новная гипотеза принимается при выполнении условия
5,0
ww
и откло-
няется в противном случае.
Рекомендации по определению необходимого объема выборки при за-
данной вероятности ошибок второго рода приводятся, например, в [12]. Там
же содержится большой набор статистических критериев для проверки дру-
гих вариантов параметрических гипотез.
Задача проверки однородности случайных выборок возникает, когда в
распоряжении исследователя имеются результаты двух или более самостоя-
тельных статистических экспериментов и желательна их совместная обработ-
ка. В таком случае необходима проверка гипотезы о принадлежности имею-
щихся выборок к одной и той же генеральной совокупности. Для пр оверки
таких гипотез применяются критерии однородности Смирнова-Колмогорова,
Вилкоксона и др.
Критерий однородности Смирнова-Колмогорова по своей форме ана-
логичен критерию согласия Колмогорова. При проверке гипотезы об одно-
родности двух случайных выборок x
1
,x
2
,…,x
n
и y
1
,y
2
,…,y
m
в качестве меры
расхождения рассматривается величина
xFxF
mynx
x
nm
,,,
max
, где
F
x,
*
n
и F
y,
*
m
- статистические функции распределения, определенные соответ-
ственно по первой и второй выборкам. Далее используется закон распреде-
ления Колмогорова (табл. 10) для случайной величины
nm
mn
.
3.8. Пример статистической имитационной модели системы со случайными
параметрами
Рассмотрим модель процесса самонаведения в вертикальной плоскости
летательного аппарата (ЛА) с радиолокационным координатором на неко-
торый объект (цель), в условиях однократного воздействия помехи типа лож-
ной цели. Целью моделирования является оценка точности системы.
Движение ЛА (в наиболее упрощенном виде) описывается линеаризо-
ванной системой дифференциальных уравнений [14]:
KK
dt
d
,
z
dt
d
,
95
в
NMLL
dt
d
z
z
,
в
рпрп
рп
в
TT
k
d
1
dt
,
v
dt
dy
ла
,
yц
ц
v
dt
dy
,
vv
dt
dD
xц
. (3.33)
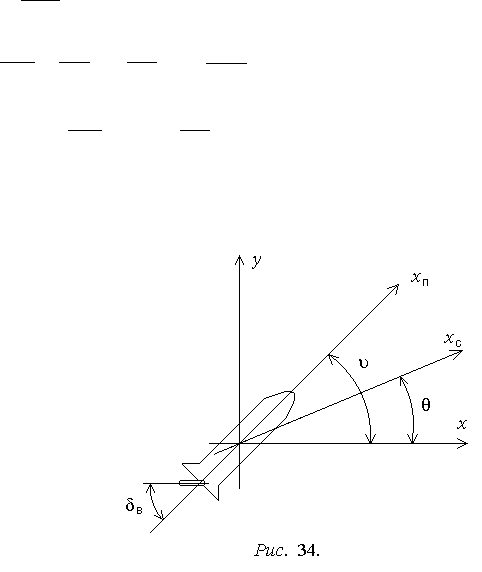
В уравнениях (3.33) использованы следующие обозначения переменных
состояния модели (рис. 34, 35): - угол наклона траектории ЛА; - угол
тангажа ЛА;
z
- скорость
изменения угла тангажа ЛА;
в
- угол отклонения рулей
высоты ЛА; y
ла
- высота ЛА;
y
ц
- высота цели; D - горизон-
тальная проекция дальности
"ЛА - цель".
Постоянные коэффици-
енты и параметры модели:
K,L,M,N - аэродинамиче-
ские коэффициенты; T
рп
,k
рп
-
постоянная времени и коэф-
фициент передачи рулевого
привода; v - скорость ЛА;
v
цx
,v
цy
- горизонтальная и
вертикальная проекции скорости цели.
Сигнал управления ЛА формируется в виде =
ст
+
сн
, где
ст
=i
1
i
2
z
- сигнал стабилизации; i
1
,i
2
- коэффициенты передачи автопилота;
сн
=-
k
сн
(
к
) - сигнал самонаведения по методу погони; k
сн
- коэффициент са-
монаведения;
к
- измеренный координатором угол наклона линии визиро-
вания цели.
Будем учитывать только детерминированные ошибки измерения, обу-
словленные наличием ложной цели.
При отсутствии ложной цели угол наклона линии визирования цели из-
меряется точно:
96
D
yy
лац
цк
.
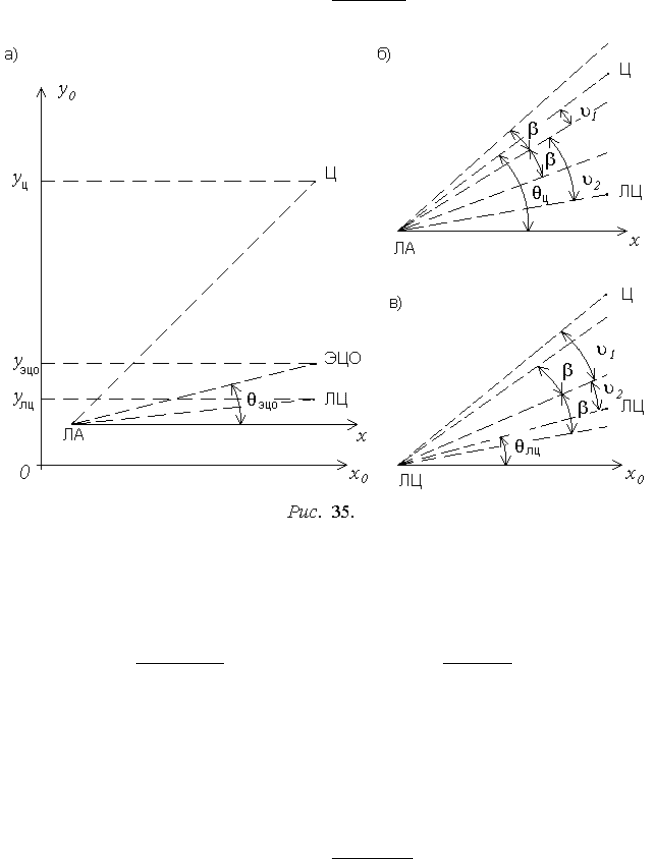
При наличии ложной цели, если в пределах диаграммы направленности
антенны координатора находятся обе цели (рис. 35,а), координатор на основе
суммарного сигнала измеряет угловое положение некоторого эффективного
центра отражения (ЭЦО):
D
yy
лаэцо
эцок
,
лцц
ц
лццлцэцо
ss
s
yyyy
, y
лц
=const,
где s
ц
и s
лц
- интенсивности радиолокационного сигнала соответственно
истинной и ложной целей.
После выхода за пределы диаграммы направленности одной из целей
(разрешения целей) координатор измеряет соответственно угловое положе-
ние истинной цели (рис. 35,б)
к
=
ц
или ложной цели (рис. 35,в):
D
yy
лалц
лцк
.
97
Для построения модели процесса наведения с учетом действия рас-
сматриваемой помехи дополним уравнения (3.33) моделью смены дискрет-
ных состояний системы управления, выделив их по признаку различия сигна-
ла управления .
Множество состояний будет иметь вид X=(x
1
,x
2
,x
3
,x
4
),
где x
1
- наведение на истинную цель:
сн
=-k
сн
(
ц
);
x
2
- наведение на ЭЦО:
сн
=-k
сн
(
эцо
);
x
3
- наведение на ложную цель:
сн
=-k
сн
(
лц
);
x
4
- отсутствие сигнала самонаведения (координатор работает в режиме
поиска цели):
сн
=0.
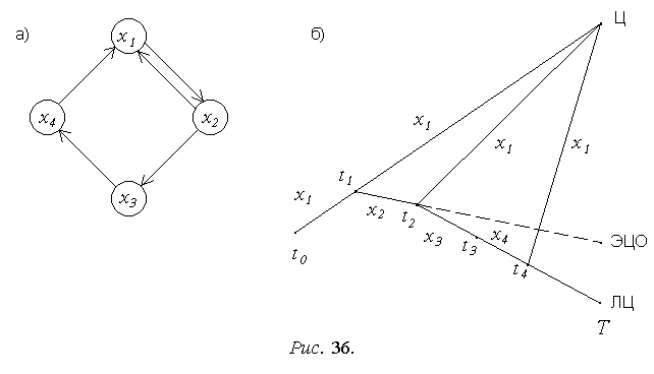
Логика смены состояний описывается графом на рис. 36,а и для случая
однократного появления ложной цели иллюстрируется схемой на рис. 36,б.
На рис. 36,б отмечены моменты времени: t
0
- начала моделируемого
процесса наведения, t
1
- появления ложной цели, t
2
- разрешения целей, t
3
-
селекции ложной цели и переключения координатора в режим поиска цели,
t
4
- повторного захвата на сопровождение истинной цели, T - окончания про-
цесса наведения.
Таким образом, на интервале времени [t
0
;T] могут иметь место сле-
дующие последовательности состояний, или фаз движения системы:
u
1
: x
1
;
u
2
:
121
xxx
;
98
u
3
:
321
xxx
;
u
4
:
4321
xxxx
;
u
5
:
14321
xxxxx
.
Переход из x
1
в x
2
возможен только в момент времени t
1
и происходит с
вероятностью p
12
. Момент t
2
и соответствующий ему переход определяются
изменением текущих координат моделируемых объектов. Интервалы време-
ни
t
3
-t
2
и
t
4
-t
3
- непрерывные случайные величины, распределен-
ные по экспоненциальному закону.
Таким образом, построенная модель реализует схему ДРС (подразд. 2.2).
Отметим также, что система (3.33) после подстановки в правую часть четвер-
того уравнения выражений для оказывается нестационарной.
Точность системы характеризуется величиной конечной ошибки :
=(T)=y
ц
(T)-y
ла
(T), (3.34)
где T определяется из условия D(T)=0.
Все параметры модели, включая начальные условия, можно разбить на
четыре группы:
1. Детерминированные (фиксированные) параметры, характеризующие
элементы системы управления ЛА: K, L, M, N, T
рп
, k
рп
, v, i
1
, i
2
, k
сн
, s
ц
, .
2. Связанный параметр, определяемый в процессе моделирования:
t
2
-t
1
.
3. Случайные параметры, характеристики распределения которых о п-
ределяются предшествующими процессами в системе: t
0
, начальные условия
0
,
0
,
z0
,
в0
, y
ла0
, D
0
, для уравнений (3.33), интервалы
и
. В эту
группу включим также дискретный параметр с двумя возможными значе-
ниями (0 при отсутствии перехода в x
2
в момент t
1
и 1 при наличии такого
перехода).
4. Неопределенные параметры, характеризующие исследуемые условия
применения системы: y
ц0
, v
цx
, v
цy
, y
лц
, s
лц
, t
1
.
Таким образом, модель является стохастической, и для показателя каче-
ства (3.34) могут быть определены только средние характеристики.
Ограничимся оценкой математического ожидания конечной ошибки
системы.
В условиях случайности и неопределенности ряда параметров в общем
случае могут быть получены условные оценки m
, соответствующие кон-
кретным значениям неопределенных параметров и конкретным законам

99
распределения случайных параметров модели. Рассматриваемая модель
нестационарной ДРС допускает только имитационное моделирование.
Пусть для моделируемой ситуации заданы:
- фиксированные значения y
ц0
, v
цx
, v
цy
, y
лц
, s
лц
, t
1
;
- законы распределения случайных параметров, которые считаются ста-
тистически независимыми:
;0
,
1
max00min00
max00min0
min0max0
0
DDDD
DDD
DD
Df
илипри
при
;00
,0
3
33
3
33
при
приe
f
;00
,0
4
44
4
44
при
приe
f
P(=1)=p
12
, P(=0)=1-p
12
;
- для остальных случайных параметров фиксированные значения.
Процедура статистического имитационного моделирования и оценки
m
для заданной ситуации будет выглядеть следующим образом.
Должны быть получены n реализаций процесса наведения, начиная с t
0
,
путем численного интегрирования на ЦВМ модели (3.33) с учетом смены
дискретных состояний системы (серия опытов объемом n).
Перед каждым i-м опытом с помощью стандартного генератора слу-
чайных чисел , распределенных по равномерному закону в интервале [0;1],
"разыгрываются" значения случайных параметров модели:
(D
0
)
i
=D
0min
+(D
0max
- D
0min
)
4i-3
,
24
3
3
1ln
1
i
i
,
14
4
4
1ln
1
i
i
,
,124
124
0
,1
p
p
i
i
i
при
при
и рассчитывается значение
xц
vv
D
T
i
i
0
.
100
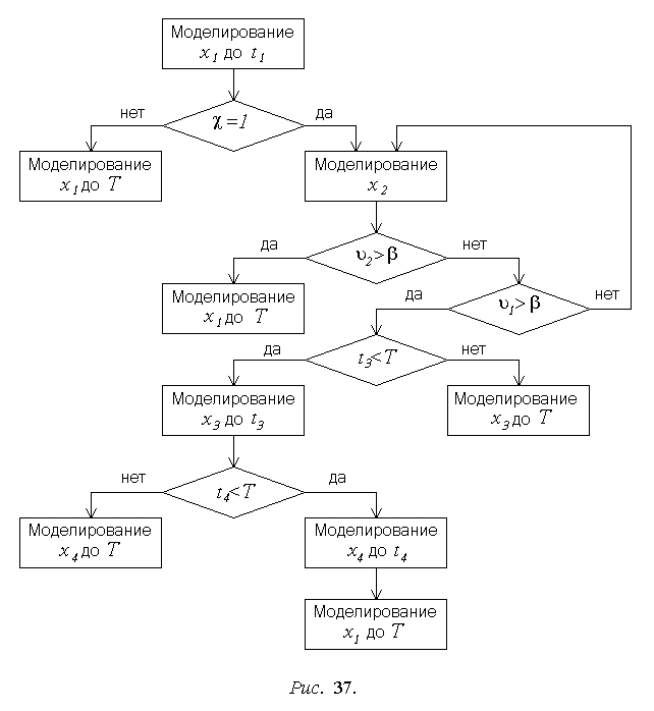
Укрупненная блок-схема получения i-й реализации процесса наведения
представлена на рис. 37. В процессе моделирования определяется (t
2
)
i
, как
момент, когда в первый раз окажется выполнено одно из условий:
1
> или
2
> (рис. 35,б,в), - и определяется дальнейшее развитие процесса: переход
12
xx
при
2
> или переход
32
xx
при
1
>. После определения (t
2
)
i
раcсчитываются (t
3
)
i
=(t
2
)
i
+(
3
)
i
и (t
4
)
i
=(t
3
)
i
+(
4
)
i
. В качестве результата i-
го опыта регистрируется
i
= y
ц
(T
i
) - y
ла
(T
i
)

101
Оценка математического ожидания конечной ошибки системы опреде-
ляется как
.
1
1
n
i
i
n
m
Необходимое количество опытов n определяется с учетом требуемой
точности результата по (3.19) или на основе соответствующего итерационно-
го алгоритма.
Отметим в заключение две особенности реализации такой модели мето-
дом статистического моделирования:
- необходимое количество опытов (имитируемых реализаций процесса
наведения) не зависит от количества учитываемых случайных параметров
модели;
- если требуется оценить показатель качества системы для различных си-
туаций, отличающихся исходными данными (разные фиксированные значе-
ния параметров или законы распределения), рассмотренная процедура в
полном объеме, включая серию опытов, должна быть повторена для каждого
варианта исходных данных.
3.9. Моделирование случайных векторов
Принятое в рассмотренном выше примере допущение о статистической
независимости случайных параметров модели позволило обеспечить исполь-
зование для каждого из них самостоятельного генератора случайных чисел. В
общем случае приходится иметь дело с совокупностью статистически зави-
симых случайных параметров. Тогда возникает задача моделирования систе-
мы случайных величин, или случайного вектора.
Случайным вектором (системой случайных величин, многомерной
случайной величиной) называется упорядоченный набор случайных величин
X=(X
1
,X
2
,…,X
n
). Составляющие случайного вектора (случайные координа-
ты) X
1
,X
2
,…,X
n
являются одномерными случайными величинами.
Рассмотрим основные характеристики случайных векторов [20], исполь-
зуемые при моделировании. Ограничимся случаем, когда координаты явля-
ются непрерывными случайными величинами.
Функция распределения вероятностей случайного вектора X представ-
ляет собой n-мерную функцию совместного распределения его координат:
F
x
(x
1
,x
2
,…x
n
)=P(X
1
<x
1
,X
2
<x
2
,…,X
n
<x
n
). (3.35)
Аналогичный смысл имеет плотность распределения:
102
n
nx
n
nx
xxx
xxxF
xxxf
...
,...,,
,...,,
21
21
21
. (3.36)
Для некоторой подсистемы m<n координат вектора X
1
,X
2
,…,X
m
по
(3.35), (3.36) могут быть определены маргинальные ФРВ и ПРВ, например:
,...,,,,
212112
xxFxxF
x
;
nnx
dxdxxxxf
xx
xxF
xxf
321
21
2112
2
2112
,...,,
,
,
. (3.37)
При m=1 получим безусловные ФРВ и ПРВ случайной координаты.
Кроме того, рассматриваются условные ПРВ одной или нескольких слу-
чайных координат, связанные с (3.36), (3.37) следующим образом:
nn
nx
n
xxf
xxxf
xxxf
,...,
,...,,
,...,
2...2
21
21
, (3.38)
nmnm
nx
nmm
xxf
xxxf
xxxxf
,...,
,...,,
,...,,...,
1...1
21
11
. (3.39)
Особое практическое значение имеют вектор математических ожиданий
координат случайного вектора
n
xxxx
mmmm ,...,,
21
, где
nnxix
dxdxdxxxxfxm
i
2121
,...,,
, i=1,2,...n, (3.40)
и матрица корреляционных моментов связи, называемая чаще просто мат-
рицей моментов:
nnnn
n
n
ijx
K
21
22221
11211
. (3.41)
Диагональные элементы матрицы (3.41) представляют собой дисперсии
случайных координат:
nnxxixixii
dxdxdxxxxfmxmXMD
iii
2121
22
,...,,
,
i=1,2,...,n.
Остальные элементы - корреляционные моменты связи случайных коорди-
нат, или ковариации:
