Емельянов В.Ю. Методы моделирования стохастических систем управления

Подождите немного. Документ загружается.

123

Передаточная функция линейной части

 

)(





Tpp

Задающее воздействие изменяется по закону g=vt. На входе действует

случайная помеха F(t) в виде белого шума с нормальным законом распреде-

ления, нулевым математическим ожиданием и спектральной плотностью S

Требуется определить математическое ожидание и среднеквадратическое

отклонение сигнала ошибки в установившемся процессе.

Выделим детерминированную и случайную составляющие сигнала

ошибки:

       

tXtmtYtgtX



 )(

. С учетом характера входных

сигналов и в соответствии с принципом суперпозиции составляющие сигнала

ошибки в линеаризованной системе будут определяться следующим обра-

зом:

(t)= x

gуст

   

tYtX





Для расчета детерминированной составляющей сигнала ошибки после

линеаризации используется структурная схема (рис. 43,а), а для расчета цен-

трированной случайной составляющей - структурная схема (рис. 43,б), где

),(

00 xx

k 

















   







 

















































,σ

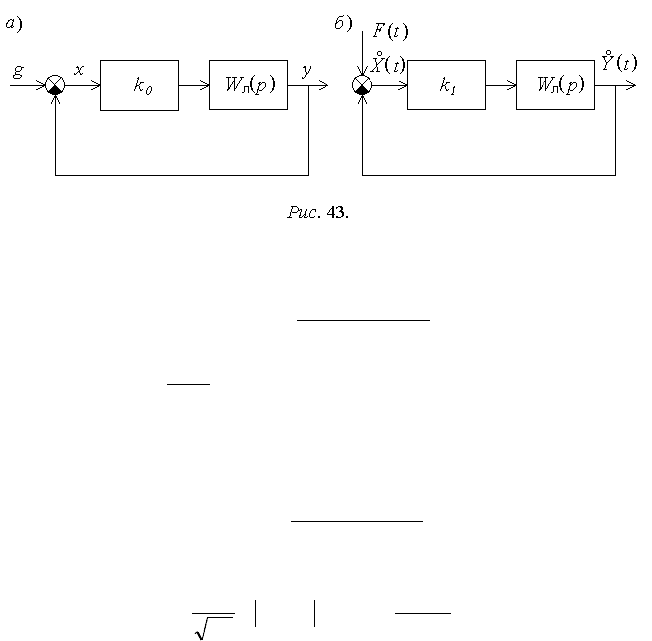
124

При расчете детерминированной составляющей передаточная функция

замкнутой системы по ошибке имеет вид:

kkpTp

pTp

pФ

)(







В результате:

 



Среднеквадратическое отклонение сигнала ошибки определяется через

дисперсию выходного сигнала и основную передаточную функцию замкну-

той системы, которая в рассматриваемом примере примет вид:

 

kkpTp





В результате:

 

Skk

dSjD

‘













, σ

При заданных k

, T и c для расчета характеристик ошибки необходимо

решить систему нелинейных алгебраических уравнений:

=σ

,σ

например, методом последовательных приближений.

125

4.5. Определение характеристик нестационарных случайных

процессов методом весовых функций

Область применения рассмотренного спектрального метода ограничена

анализом установившихся случайных процессов в стационарных системах

при стационарных воздействиях. Одним из возможных методов опр еделения

характеристик нестационарных случайных процессов в системах управления

является метод весовых функций.

Если известна весовая функция системы w(t,τ), то выходной сигнал Y(t)

при заданном входном сигнале G(t) и нулевых начальных условиях определя-

ется следующим соотношением (интегралом свертки) [3]:

     





dGtwtY

, (4.23)

справедливым как для детерминированных процессов, так и для реализаций

случайных процессов в системе.

Усреднив левую и правую части соотношения (4.23) по множеству реа-

лизаций, получим соотношение для определения математического ожидания

выходного сигнала:

     





dmtwtm

, (4.24)

где m

(τ) – математическое ожидание нестационарного входного сигнала.

Аналогично может быть определена корреляционная функция:

       





1 2

0 0

2121

'',',,,

t t

ddKtwtwttK

, (4.25)

где K

(τ, τ’) – корреляционная функция нестационарного входного сигнала.

При t

= t

из (4.25) получается соотношение для дисперсии:

         





t t

gyy

ddKtwtwttKtD

0 0

'',',,,

. (4.26)

Особый практический интерес представляет определение характеристик

переходного процесса в стационарной системе при стационарном входном

сигнале. Такой процесс является нестационарным, и для него, как частного

случая, из (4.23)-(4.26) вытекают следующие соотношения:

126

         





dtGwdGtwtY

   





dwmtm

       





1 2

0 0

1221

'' ',

t t

ddttKwwttK

         





t t

gyy

ddKwwttKtD

0 0

''',

где w(τ) – весовая функция стационарной системы; m

=const –

математическое ожидание стационарного входного сигнала; K

(τ – τ’) –

корреляционная функция стационарного входного сигнала.

Пример. Определим математическое ожидание и дисперсию выходного

сигнала апериодического звена первого порядка при входном сигнале в виде

белого шума: K

(τ) = G

δ(τ), с m

= const при нулевых начальных услови-

ях:

   







   

tekm

ekmde

mtm



























   













t t

ddGee

0 0

Учитывая свойство δ-функции

     









udu '''

для дисперсии получим:

   

dGe























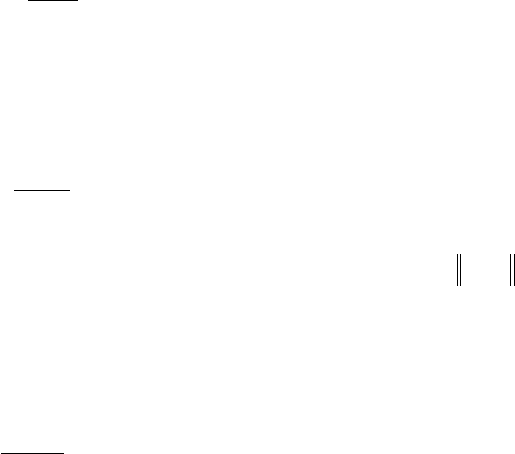
127

Рассмотренный пример относится к числу простейших. Вычисления,

очевидно, усложнятся, если рассматривать систему более высокого порядка

или определять корреляционную функцию. Для нестационарной системы

аналитические решения достаточно сложно получить даже для простейших

случаев.

4.6. Моделирование нестационарных случайных процессов в

линейных системах методом динамики средних

Рассмотрим линейную нестационарную систему, описываемую урав-

нениями:

 

       

tutbtxta

tdx

kik





1

, i=1,2,...,n, (4.27)

где a

(t), b

(t) – известные функции времени; x

(t) – фазовые переменные;

(t) – входные сигналы. Аналогичная система уравнений будет справедлива

для случайного процесса, вызванного действием на систему случайных вход-

ных сигналов. Ограничимся случаем, когда входные сигналы – коррелиро-

ванные (статистически зависимые) белые шумы:

 

       

tUtbtXta

tdX

kik







i=1,2,...,n, (4.28)

где X

(t) – случайные фазовые переменные; U

(t) – белые шумы с матема-

тическими ожиданиями

 

и матрицей интенсивностей (4.13):

 

,tG

i=1,2,...,n, j=1,2, ...,n.

Система (4.28) позволяет определять отдельные реализации случайного

процесса в системе, описываемого вектором фазовых переменных

X(t)=(X

(t),X

(t),…,X

(t)). Усреднив уравнения (4.28) по множеству реали-

заций, получим систему уравнений для математических ожиданий:

 

       

tmtbtmta

tdm

xik







i=1,2,...,n. (4.29)

Решением системы (4.29) при заданных начальных условиях

 

i=1,2,...,n, могут быть определены законы изменения во времени математи-

ческих ожиданий всех фазовых переменных системы.

Как было указано выше, для получения полного представления о про-

цессе в системе желательно получить матрицу корреляционных функций

(4.10). В связи со сложностью такой задачи обычно ограничиваются опр еде-

128

лением дисперсий фазовых переменных. В рамках метода динамики средних

это удается сделать на основе системы уравнений для корреляционных мо-

ментов фазовых переменных

     













 tXtXMt

jiij



образующих матрицу (4.12).

Вычитая уравнения (4.29) из соответствующих уравнений (4.28), получа-

ем систему уравнений для центрированных случайных составляющих фазо-

вых переменных и входных сигналов:

 

       

tUtbtXta

tXd











i=1,2,...,n. (4.30)

Найдем теперь производные корреляционных моментов, используя ли-

нейность операций дифференцирования и усреднения:

 

   































tXd

XMX

tXd







i=1,2,...,n; j=1,2,...,n. (4.31)

Подставим в (4.31) выражения для производных центрированных состав-

ляющих (4.30):

 

           























tXtUtbtXtXtaM



           





















tXtUtbtXtXtaM



       

 

           

































tXtUMtbtXtUMtbttatta

kijkkjik



Для случая, когда входные сигналы U

(t) – белые шумы – справедливы

следующие соотношения [32]:

       

tGtbtXtUM

ijjji

















       

tGtbtXtUM

jiiij

















В итоге с учетом симметричности матрицы интенсивностей G

(t)=G

(t)

получим:

 

       

 

     

tGtbtbttatta

ijji

kijkkjik







1

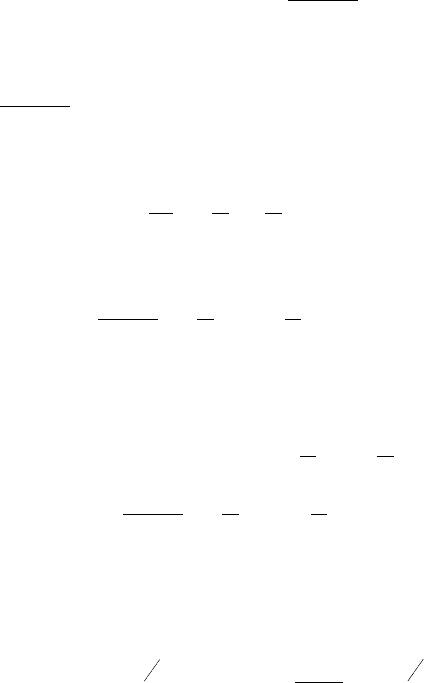
129

i=1,2,...,n; j=1,2,...,n. (4.32)

Для системы n порядка матрица моментов содержит n

элементов, ко-

торые могут быть определены решением n

уравнений (4.32) при заданных

начальных условиях 

(0), i=1,2,...,n; j=1,2,...,n. Но благодаря симметрич-

ности матрицы моментов количества независимых переменных 

и незави-

симых уравнений в (4.32) оказываются равны

)1( nn

Необходимо отметить, что даже если требуется определить только дис-

персии одной или нескольких фазовых переменных, необходимо совместно

решать все

)1( nn

уравнений (4.32).

Пример 1. Апериодическое звено 1-го порядка описывается дифферен-

циальным уравнением

Tdt



В соответствии с (4.29) уравнение для математических ожиданий им еет

идентичный вид:

 

   

Tdt

tdm



Получим уравнение для дисперсии, учитывая единственную фазовую

переменную X

= X и единственный входной сигнал в форме белого шума

= U с интенсивностью G(t):

n = 1,

   

ttD



a 

b 

 

   

Tdt

tdD



При заданных m

(t), G(t) и начальных условиях m

(0), D

(0) интегриро-

ванием полученных уравнений определяются m

(t) и D

(t). В частности, при

(0)=D

(0)=0, m

(t)=m

=const и G(t)=G

=const получим решение анали-

тически:

   

tekmtm

















   

















что совпадает с результатами, полученными для аналогичного примера м е-

тодом весовых функций.

130

Пример 2. Система 2-го порядка описывается уравнением

 

     

tubtyta

tdy

tyd

021



Требуется определить математическое ожидание и дисперсию выходно-

го сигнала при действии на входе белого шума с характеристиками m

(t), и

G(t).

Введем фазовые переменные x

= y,

x 

и перейдем к системе

уравнений в нормальной форме:

11212111

ubxaxa



22222121

ubxaxa



где a

=0, a

=1,

 

a 

 

a 

=0,

 

b 

=0,

=u(t).

В соответствии с (4.29) получим систему уравнений для определения

математических ожиданий фазовых переменных:

121

11211 uxx

mbmama



221

22221 uxx

mbmama



или с учетом условий задачи:



uxx



. (4.33)

Составим теперь уравнения для корреляционных моментов:

12112211211111111

Gbaaaa





12212122221211211211

Gbbaaaa





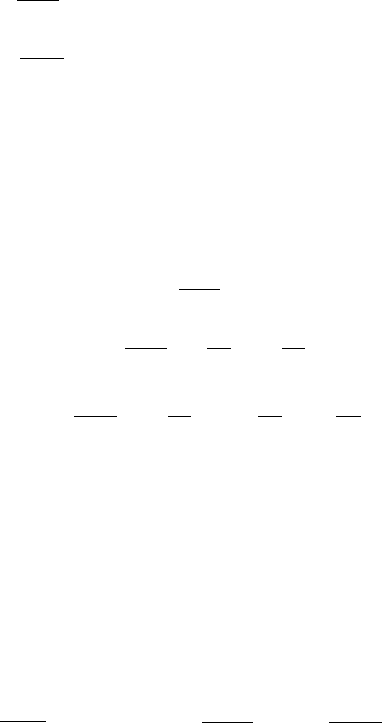
131

21122212212212111121

Gbbaaaa





22222222212211221

Gbaaaa





где

11 yx

DD 

– дисперсии фазовых переменных,



=

– корреляционные моменты связи фазовых переменных,

=0, G

=G(t). Отметим совпадение правых частей 2-го и 3-го

уравнений. Учитывая это обстоятельство, равенство 

и 

и условия зада-

чи, получим в итоге:





2221

221





(4.34)

222

22 G





Для определения законов изменения математического ожидания и дис-

персии выходного сигнала системы необходимо решить системы уравне-

ний (4.33) и (4.34) при заданных начальных значениях

mm 



, 

и 

, законах изменения параметров системы и входного сигнала

каким-либо численным методом.

Достаточно простое аналитическое решение может быть получено

только в стационарном случае для установившегося процесса. Тогда в (4.33)

и (4.34) производные можно положить равными нулю, и результат находится

решением систем линейных алгебраических уравнений:



2112



4.7. Моделирование нестационарных случайных процессов в

нелинейных системах методом динамики средних

Уравнения метода динамики средних получены на основе линейной м о-

дели системы в виде (4.27). Тем не менее этот метод в аналогичной форме

132

может быть применен и к нелинейной системе в сочетании с методом стати-

стической линеаризации. Для этого модель нелинейной системы должна

быть представлена в канонической форме:

 

          

,,...,,,

tUtbtXtXtXt

tdX

iini



i=1,2,...,n, (4.35)

где 

– нелинейные функции; X

– фазовые переменные системы; U

–

входные сигналы – белые шумы с математическими ожиданиями

 

матрицей интенсивностей (4.13). При такой форме модели входными сигна-

лами нелинейностей являются фазовые переменные системы, которые будем

рассматривать в виде сумм математических ожиданий и центрированных

случайных составляющих:

     

tXtmtX





После статистической линеаризации содержащихся в уравнениях (4.35) n

нелинейностей модель примет вид

 

     

tUtbtXk

tdX

jiji







i=1,2,...,n, (4.36)

где















– средние статистические характеристики нелиней-

ностей,















ijij

tkk

– коэффициенты усиления нелинейностей по

случайным составляющим входных сигналов,

 

xxxx

mmm ,...,,

m

–

вектор математических ожиданий фазовых переменных;



– мат-

рица корреляционных моментов связи фазовых переменных вида (4.12).

Коэффициенты статистической линеаризации 

и k

определяются

для каждой нелинейности 

на основе (4.22) или других полученных в под-

разд. 4.3 соотношений.

После усреднения уравнений (4.36) по множеству реализаций получим

систему уравнений для определения математических ожиданий фазовых

переменных:

 

   

,,,

tmtbt

tdm

uixi



i=1,2,...,n. (4.37)