Емельянов В.Ю. Методы моделирования стохастических систем управления

Подождите немного. Документ загружается.

133

После вычитания уравнений (4.37) из соответствующих уравнений (4.36)

получим систему уравнений для центрированных случайных составляющих

фазовых переменных:

 

     

,,,

tUtbtXtk

tXd

xij











i=1,2,...,n. (4.38)

Теперь, выполнив преобразования, аналогичные примененным к сис-

теме (4.30), получим систему уравнений для корреляционных моментов свя-

зи фазовых переменных:

 

     

,,,,,

tGtbtbttkttk

ijji

lixjlljxil









i=1,2,...n; j=1,2,...n. (4.39)

Полученные системы уравнений (4.37) и (4.39) справедливы как для ста-

ционарных, так и для нестационарных систем и формально аналогичны

уравнениям динамики средних линейной системы (4.29), (4.32). Но здесь ко-

эффициенты уравнений 

и k

, в отличие от a

, зависят от текущих значе-

ний решений уравнений. То есть, в строгом смысле, уравнения (4.37) и (4.39)

являются нелинейными. Поэтому для их решения даже в простейших случаях

требуется применение численных методов. При этом на каждом шаге интег-

рирования необходимо определять новые значения коэфф ициентов 

и k

путем решения систем нелинейных уравнений для определения коэффициен-

тов статистической линеаризации с учетом текущих значений

и θ

4.8. Построение моделей случайных процессов в дискретных системах

Для описания случайных процессов в дискретных системах используют-

ся те же характеристики, как и для непрерывных систем, но здесь вместо не-

прерывного времени они рассматриваются как функции дискретного аргу-

мента n. Ограничимся рассмотрением одномерного случайного процесса.

Математическое ожидание случайного процесса рассматривается в

форме m

(n)=MX(n), если процесс наблюдают в дискретные моменты

времени t=nT

- шаг дискретизации времени, n - целое число), или

(n,)==MX(n,), если процесс наблюдают в смещенные моменты вре-

мени t=(n+)T

( - смещение, 01).

Корреляционная функция определяется в форме

134

               

 

1111

, nmnXnmnXMnXnXMnnK

xxx



















или соответственно

(n,,n

,

)=M[(X(n,)-m

(n,))( X(n

,

)- m

,

))].

Значение корреляционной функции при n=n

и =

дает дисперсию

случайного процесса:

(n,n)=D

(n), К

(n,,n,)=D

(n,).

Для стационарного процесса m

(n,)=m

=const, K

(n,,n

,

)=K

-n).

Аналогичные замены аргументов выполняются для функций ПРВ и

ФРВ, а также для всех средних характеристик многомерных случайных про-

цессов.

Все рассмотренные методы построения моделей случайных процессов

применимы и для дискретных систем с некоторыми отличиями, обусловлен-

ными особенностями их описания:

- вместо дифференциальных уравнений используются разностные;

- вместо преобразования Лапласа используется z-преобразование и да-

лее для применения частотных и спектральных методов - w-преобразование,

переход к псевдочастоте и так далее.

Рассмотрим особенности построения моделей случайных процессов в

дискретных системах на примере метода весовых функций.

Весовая функция нестационарной дискретной системы определяется в

виде w(n,,k), где n,k - целые числа,  - смещение (01). Для стационар-

ной системы: w(n-k,) или w(n,), считая формально k=0.

При заданном входном сигнале G(n) и известной весовой функции вы-

ходной сигнал дискретной системы определяется конечной суммой:

     







kGknwnY

,,,

, (4.40)

являющейся аналогом интеграла свертки (4.23) для непрерывной системы.

Здесь G и Y - реализации случайных процессов.

Усреднив (4.40) по множеству реализаций, получим формулу для опре-

деления математического ожидания выходного сигнала:

     







kmknwnm

,,,

. (4.41)

Для корреляционной функции также имеет место соотношение, анало-

гичное (4.25),

135

       



 



lkKlnwknwnnK

0 0

1111

,,,,,,,,

(4.42)

или для дисперсии

       



 



lkKlnwknwnD

0 0

,,,,,,

. (4.43)

Если входной сигнал представляет собой белый шум K

(k,l)=G



, где



=(k-l) - единичная импульсная функция, вторая сумма в соотношении

(4.43) сокращается до одного слагаемого:

   

knwGGlnw

,,,,







и в результате

   







knwGnD

.,,,

(4.44)

Для стационарной системы и несмещенных моментов времени соо тно-

шения (4.40)-(4.44) принимают вид

         







knGkwkGknwnY

         







knmkwkmknwnm

       



 



lkKlnwknwnnK

0 0

       



 



lkKlnwknwnD

0 0

     







kwGknwGnD

(4.45)

4.9. Методы моделирования случайных процессов с заданными характери-

стиками

Применение рассмотренных выше методов математического модели-

рования случайных процессов в системах управления связано с рядом огр а-

ничений. Построение аналитических моделей возможно только в простейших

136

случаях, а наиболее универсальный из рассмотренных метод динамики сред-

них требует численного интегрирования. Порядок модели, построенной по

методу динамики средних, в несколько раз превышает порядок моделируе-

мой системы, а входные воздействия могут учитываться только в форме бе-

лых шумов. Поэтому для достаточно сложных задач неизбежно использова-

ние статистического имитационного моделирования, несмотря на высокую

его трудоемкость. Кроме того, статистическое имитационное моделирование

применяется для проверки точности и достоверности результатов, получен-

ных другими методами, требующими более жестких допущений о характери-

стиках моделируемых процессов.

При статистическом имитационном моделировании на основе матема-

тических, полунатурных и других моделей возникает задача имитации

внешних воздействий на систему, имеющих форму случайных процессов с

определенными характеристиками. Эта задача решается путем построения

генераторов случайных процессов.

Рассмотрим задачу имитации одномерного случайного процесса X(t).

Получаемые реализации должны подчиняться закону распределения с задан-

ной ПРВ f(x) и иметь заданную корреляционную функцию K

(). Генератор

случайного процесса с заданными характеристиками обычно строится на

основе генератора белого шума.

При математическом моделировании используются стандартные гене-

раторы псевдослучайных чисел с равномерным или нормальным законом

распределения. Такие генераторы обычно обеспечивают получение после-

довательностей чисел с достаточно низкой взаимной зависимостью. Если

рассматривать такую последовательность 

,

,…,

как последова-

тельность значений процесса (t), зарегистрированных в моменты времени

<<t

с постоянным шагом t: (t

)=

, (t

)=

, 

(t

)=

, (t

)=

, t

i+1

+t, будет получена модель дискретного белого

шума. При t0 перейдем к модели непрерывного белого шума. При ис-

пользовании ЦВМ шаг t всегда конечен. Поэтому его величину приходится

учитывать при расчете параметров цифровых моделей непрерывных случай-

ных процессов.

Для получения случайного процесса с названными выше характеристи-

ками из белого шума с равномерным или нормальным законом распределе-

ния необходимо обеспечить: заданный закон распределения - эта задача ре-

шается рассмотренными выше методами безынерционных нелинейных пре-

137

образований; заданные корреляционные свойства - эта задача решается ме-

тодами формирующего фильтра, скользящего суммирования и др.

4.9.1. Метод формирующего фильтра

Метод формирующего фильтра основан на использовании закономер-

ностей преобразования линейным динамическим звеном спектральной

плотности случайного сигнала, описываемых соотношением (4.15). Если на

вход динамического звена поступает белый шум со спектральной плотно-

стью S



()=S

, спектральная плотность выходного сигнала X(t) будет опре-

деляться через частотную передаточную функцию звена W(j) следующим

образом:

()=|W(j)|

Формирующим фильтром называется динамическое звено, обеспечи-

вающее требуемые корреляционные свойства выходного сигнала.

Модель случайного процесса с заданной корреляционной функцией

() можно построить на основе формирующего фильтра, используя в

качестве его входного сигнала белый шум. Необходимая передаточная функ-

ция формирующего фильтра определяется из соотношения

 





, (4.46)

где

   









 deKS

Пример. Задана корреляционная функция моделируемого процесса

()=D

-| |

Определим его спектральную плотность:

 

   





















deDdeDdeeDS

 

 

 

 

























jdeD

138

   





























xxx

Пусть имеется генератор белого шума (t) с постоянной интенсивно-

стью, или дисперсией, G

. Определим его спектральную плотность:



()=G

(),

   

GeGdeGS















Теперь найдем передаточную функцию формирующего фильтра:

 























откуда

 

1+Tj





или

 

1+pT

pW 

, где



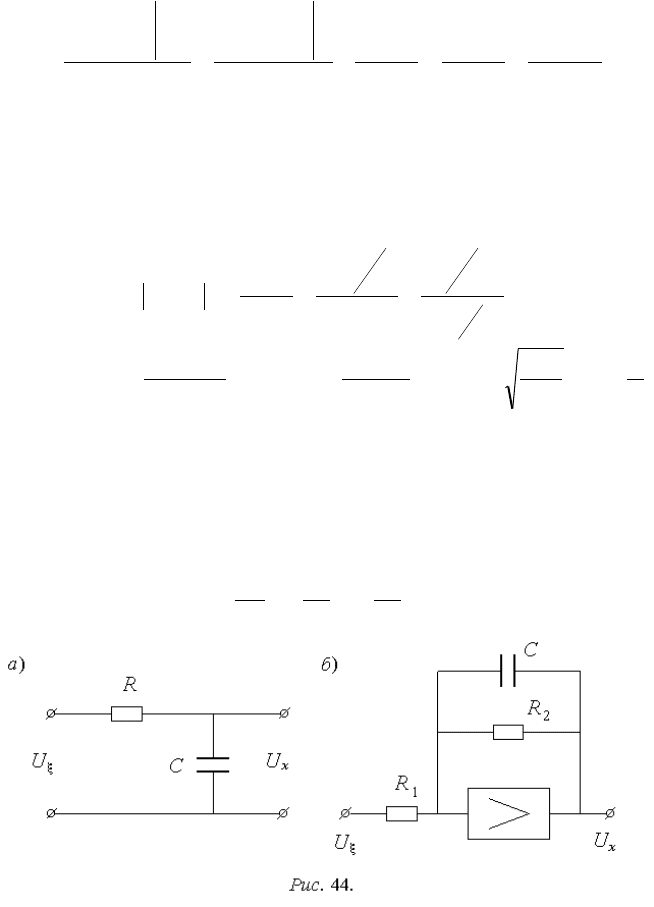
Такой формирующий фильтр может быть физически реализован, на-

пример, в виде четырехполюсника (рис. 44, а) или на операционном усилите-

ле (рис. 44, б). Для четырехполюсника k

=1, T

=RC; для операционного

усилителя k

, T

C. В математической модели, построенной на

основе D-схемы, такой формирующий фильтр может быть представлен

дифференциальным уравнением:



Tdt

dX 1

139

При реализации на ЦВМ математической модели непрерывной системы

в форме (4.27) или (4.35) и использовании методов пошагового интегрирова-

ния дифференциальных уравнений фактически применяется аппроксимация

непрерывного случайного процесса дискретным. Такой дискретный процесс

имеет период дискретизации, равный шагу интегрирования h, и сохраняет

свое значение в течение периода. Определим корреляционную функцию и

спектральную плотность дискретного случайного процесса, аппроксими-

рующего непрерывный белый шум с интенсивностью G



()=G

1()-G

1(-h),

     

 



















deGdehGS

 

hGhj

111 













Поэтому, если в качестве источника белого шума используется генера-

тор случайных чисел с некоторым законом распределения, характеризуемым

дисперсией D



, в соотношении (4.46) в качестве спектральной плотности

входного сигнала для формирующего фильтра следует брать значение



h. Например, при использовании стандартного генератора псевдослу-

чайных чисел с равномерным законом распределения в интервале [0; 1] сле-

дует брать S

=h/12.

Отметим, что область использования формирующих фильтров не о гра-

ничивается статистическим имитационным моделированием. Так получен-

ные выше основные соотношения метода динамики средних могут использо-

ваться только в предположении, что входные сигналы системы являются бе-

лыми шумами. Если необходимо учесть входной сигнал в виде случайного

процесса с заданной корреляционной функцией, следует добавить в исход-

ную систему уравнений (4.27) или (4.35) соответствующее уравнение форми-

рующего фильтра.

4.9.2. Метод скользящего суммирования

Метод формирующего фильтра удается использовать, только если за-

данная корреляционная функция моделируемого случайного процесса по-

зволяет получить передаточную функцию фильтра рассмотренным выше

способом. Во многих случаях заданный вид корреляционной функции не

140

позволяет это сделать. Тогда приходится видоизменять заданную корреляци-

онную функцию или использовать иные методы.

Метод скользящего суммирования свободен от указанного ограниче-

ния. Он применяется при цифровом моделировании дискретных или слу-

чайных непрерывных процессов и может рассматриваться как модификация

метода формирующего фильтра.

Рассмотрим сначала более простой случай, когда вид заданной корре-

ляционной функции позволяет подобрать передаточную функцию форм и-

рующего фильтра. Тогда на основе обратного преобразования Лапласа оп-

ределяется весовая функция фильтра w(t)=L

-1

[W(p)]. Метод основан на

использовании интеграла свертки

     





dtwtX

где X(t) - реализация выходного сигнала - случайного сигнала с заданной

корреляционной функцией; (t) - реализация случайного входного сигнала

(белого шума).

При цифровом моделировании интеграл свертки реализуется в виде

суммы, что эквивалентно приближенному интегрированию по методу пря-

моугольников:

     











knk

hwhkhnhkhwnx

, (4.47)

t=nh, w

=w(kh), 

n-k

=[(n-k)h].

Для моделирования случайного дискретного процесса непосредственно

используется дискретная форма интеграла свертки:

     







knkwnx

. (4.48)

Иногда удобнее использовать соотношения, эквивалентные (4.47)-(4.48):

 









kkn

hwnx

, w

n-k

=w[(n-k)h], 

=(kh), (4.49)

     







kknwnx

. (4.50)

Поясним вычислительную процедуру метода скользящего суммирова-

ния с помощью временной диаграммы (рис.45). Для вычисления значения

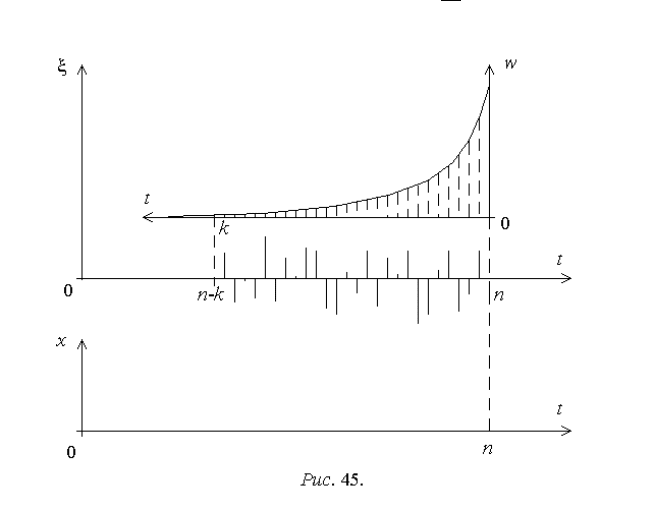
141

процесса на n-м шаге x(n) суммируются произведения совпадающих по

вертикали значений  и w.

Для вычисления следующего значения x(n+1) верхний график сдвига-

ется вправо на один шаг и так далее. При практической реализации метода

количество слагаемых "скользящей" суммы принимается постоянным. Для

точного воспроизведения заданной корреляционной функции оно должно

соответствовать интервалу затухания t

весовой функции до (35)% от ее

максимального значения, например, в (4.47)

 









knk

hwnx

nn 

В зависимости от соотношения t

и h может потребоваться до 100 и бо-

лее слагаемых. Поэтому вычислительная трудоемкость метода скользящего

суммирования, как правило, оказывается значительно выше трудоемкости

метода формирующего фильтра.

Этот недостаток вполне компенсируется возможностью воспроизведе-

ния произвольной формы корреляционных функций. Для рассмотренного

выше примера воспроизведения корреляционной функции вида

142

()=D

-| |

весовая функция формирующего фильтра имеет вид

 

























 e

T+Tj

Можно показать, что и в общем случае для корреляционной функции

произвольной формы, удовлетворяющей условию |K()|<<, может быть

формально получена функция w(), позволяющая получать на основе инте-

грала свертки реализации процесса X(t) с такой корреляционной функцией,

даже если соответствующий формирующий фильтр в форме динам ического

звена физически не реализуем. Если при этом в качестве (t) используется

белый шум, то получаемая w() будет совпадать с K() с точностью до

масштабного коэффициента. Поэтому для формирования с помощью метода

скользящего суммирования случайного процесса с заданной корреляцион-

ной функцией K

() произвольного вида можно порекомендовать использо-

вать K

() непосредственно в качестве весовой функции в соотношениях

(4.47)-(4.50) с последующим масштабированием получаемых значений слу-

чайного процесса с учетом соответствия обеспечиваемой корреляцио нной

функции заданной. Здесь можно ограничиться сравнением получаемой вы-

борочной дисперсии D

и значения K

(0). Если оказывается, что

 

sKD





, следует уменьшить центрированную составляющую полу-

чаемого процесса в

раз (пропорционально отношению среднеквадрати-

ческих отклонений).

4.9.3. Особенности практической реализации генераторов случайных пр о-

цессов

Как следует из вышеизложенного, процедура формирования случайно-

го процесса с заданными характеристиками должна предусматривать два

последовательных этапа преобразования исходного процесса в форме белого

шума: формирование заданного закона распределения и обеспечение задан-

ных корреляционных свойств. Проанализируем взаимное влияние этих пр е-

образований.

Преобразование закона распределения одним из рассмотренных выше

методов можно рассматривать как преобразование сигнала нелинейным

безынерционным звеном. Например, для метода обратных функций статиче-