Емельянов В.Ю. Методы моделирования стохастических систем управления
Подождите немного. Документ загружается.


113
где m
g
(t) - детерминированная составляющая, или математическое ожидание
входного сигнала;
)(tG
- центрированная случайная составляющая входного
сигнала (случайный процесс с нулевым математическим ожиданием).
Модель преобразования детерминированной составляющей строится на
основе стандартного аппарата передаточных функций:
L[m
y
(t)] = Φ(p)L[m
g
(t)],
где L[m
g
(t)], L[m
y
(t)] - изображения по Лапласу детерминированных состав-
ляющих соответственно входного и выходного сигналов; Φ(p) - передаточная
функция звена или системы.
Выходной сигнал в установившемся процессе может быть определен по
теореме о конечном значении:
tmLpptmm
g
p
y
t
y
0
lim)(lim
уст
(4.14)
Например, при m
g
(t)=const для асимптотически устойчивой системы
из (4.14) получим: m
y
=Φ(0)m
g
=const.
Модель преобразования центрированной случайной составляющей
строится для спектральных плотностей
S
y
(ω)=|Φ(jω)|
2
S
g
(ω), (4.15)
где спектральная плотность входного сигнала определяется по его корреля-
ционной функции
.
deKS
j
gg
По полученной спектральной плотности выходного сигнала находят его
дисперсию:
,
2
1
dSD
yy
(4.16)
Интеграл вида (4.16) обычно удается привести к форме:
d
jgjg
jh
I
nn
n
n
2
1
,
где h
n
(jω)=b
1
(jω)
2n-2
+b
2
(jω)
2n-4
+...+b
n
, g
n
(jω)=a
0
(jω)
n
+a
1
(jω)
n-1
+...+a
n
.
Тогда:

114
n
n
n
n
a
I
0
1
)(
2
'
1
,
где ∆
n
- n-й определитель Гурвица для многочлена g
n
(p) [3], а ∆
'
n
получается
из ∆
n
заменой 1-й строки коэффициентами многочлена h
n
. Например, при
n=4
420
31
420
31
4
0
00
0
00
aaa
aa
aaa
aa
,
420
31
420
4321
4
0
00
0
'
aaa
aa
aaa
bbbb
.
Для системы с несколькими случайными входными сигналами ограни-
чимся случаем, когда они не коррелированы между собой.
Тогда математическое ожидание и дисперсия выходного сигнала опре-
деляются на основе принципа суперпозиции:
mLppm t
k
G
y
k
G
K
k
p
y
)(
1
0
lim
,
dSjΦD
K
k
k
G
y
k
G
y
1
2
)()(
2
1
, (4.17)
где
tm
k
G
и
k
G
S
- математическое ожидание и спектральная плотность
k-го входного сигнала (задающего или возмущающего воздействия);
tGtmtG
k
k
Gk
;
p
y
k
G
- передаточная функция системы от k-го
входа к выходу.
Таким образом, выходной сигнал определяется в форме
tYtmtY
y
, причем центрированная случайная составляющая опи-
сывается дисперсией D
y
.
Аналогичный подход используется при нахождении ошибки системы.
Она определяется в форме:
tXtmtX
x
. Пусть на систему действу-
ют детерминированное задающее воздействие g(t) и несколько некоррели-
рованных случайных возмущений
tFtmtF
k
k
fk
, k=1,2,…,K.
Тогда математическое ожидание ошибки определяется в виде суммы:
115
K
k
k
yfg
K
k
k
xfgyx
mxmxg - mm
11
устуст
,
где
tgLppx
x
p
g
0
lim
уст
,
tmLppm
k
k
k
f
y
F
p
yf
0
lim
, Φ
x
(p) - пе-
редаточная функция системы по ошибке от задающего воздействия,
p
y
k
F
- передаточная функция системы по k-му возмущающему воздействию,
k=1,2,...,K.
Дисперсия ошибки совпадает с дисперсией выходного сигнала, опре-
деляемой в соответствии с (4.17). Примеры использования рассмотренного
метода широко представлены в литературе [32, 33].
4.3. Статистическая линеаризация нелинейной стационарной
системы
Если моделируемая система включает в себя хотя бы одно нелинейное
звено, задача анализа протекающих в ней процессов существенно усложня-
ется. Для нелинейных систем не выполняется принцип суперпозиции. Нели-
нейное звено вносит существенные искажения в закон распределения преоб-
разуемого сигнала. Тем не менее возможность использования достаточно
простых методов анализа случайных процессов, разработанных для линейных
систем, удается здесь обеспечить на основе статистической линеаризации
системы.
Статистической линеаризацией называется построение линейной моде-
ли нелинейного звена системы управления с учетом характеристик преобра-
зования случайного сигнала линейной частью системы.
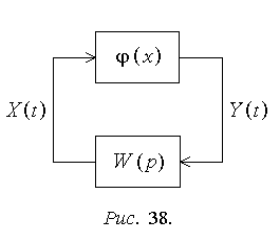
Методы статистической линеаризации основаны на допущении о нали-
чии у линейной части системы свойства фильтра. Благодаря этому, сигнал на
входе нелинейного звена, то есть на
выходе линейной части (рис. 38),
рассматривается в форме
tXtmtX
x
, причем для
описания центрированной состав-
ляющей ограничиваются дисперсией
D
x
или среднеквадратическим от-
клонением σ
x
. При нескольких вход-
ных сигналах для каждого использу-
116
ется аналогичное представление, а для описания совокупности центрирован-
ных составляющих - матрица моментов (4.12).
Статистическая линеаризация проводится для стационарных процессов
или для фиксированных значений m
x
и σ
x
нестационарного случайного про-
цесса, соответствующих некоторо-
му рассматриваемому моменту
времени.
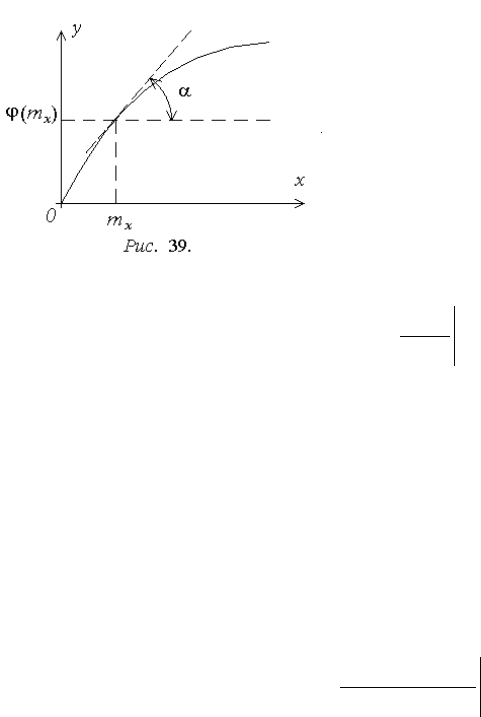
Если статическая характери-
стика нелинейного звена (x) одно-
значна и дифференцируема по
крайней мере для отрезка [m
x
-3σ
x
;
m
x
+3σ
x
] и
x
достаточно мала,
выполняется прямая линеаризация
нелинейности в окрестности m
x
(рис. 39). В этом случае сигнал на
выходе нелинейного звена рассмат-
ривается в форме:
XmmY
xx
'
,
tg
mx
x
x
m
x
x
'
, (4.18)
где (m
x
) и '(m
x
) - коэффициенты линеаризованной модели нелинейного
звена, нелинейно зависящие от m
x
; - угол наклона касательной к функции
(x) в точке m
x
. Получаемая приближенная зависимость (4.18) оказывается
линейной относительно центрированной составляющей входного сигнала
X
, что равноценно замене исходной нелинейной статической характери-
стики звена касательной в точке, соответствующей m
x
.
Для нелинейного звена с несколькими входами статическая характери-
стика приводится к виду (x
1
,x
2
,…,x
n
). При выполнении для всех входных
сигналов x
i
указанных выше условий прямая линеаризация осуществляется в
следующей форме:
n
i
i
x
i
n
xxx
X
mx
x
xxx
mmmY
n
1
21
,...,,
),...,,(
21
,
i
xi
XmX
i
, i=1,2,...,n,
где условие x=m
x
выполняется для всех аргументов функции .
117
Таким образом, принцип линеаризации стохастических нелинейных сис-
тем аналогичен принципу линеаризации детерминированных систем. Но
здесь линеаризация производится не в окрестности состояния равновесия, а в
окрестности средних значений (математических ожиданий) входных сигналов.
Если нелинейность является неоднозначной или имеет разрывы 1-го или
2-го рода в пределах отрезка [m
x
-3σ
x
; m
x
+3σ
x
], применяется статистическая
линеаризация, состоящая в приближенной замене нелинейной характеристи-
ки звена эквивалентной в вероятностном смысле линеаризованной зависи-
мостью между входными и выходной переменными.
Рассмотрим сначала звено с одним входом и статической характеристи-
кой (x). В зависимости от вида статической характеристики возможны раз-
личные варианты получаемой линеаризованной зависимости.
Для однозначной нелинейности общего вида:
XkY
10
.
Для однозначной нечетной относительно входного сигнала нелинейно-
сти (-x)=- (x) коэффициент
0
выражают через математическое ожи-
дание входного сигнала:
0
= k
0
m
x
.
Для неоднозначной нелинейности линеаризованную зависимость полу-
чают в форме:
2
2
1
10
XkXkY
, где X
1
=X,
dt
dX
X
2
.
Коэффициент
0
называется средней статистической характеристикой
нелинейности; коэффициент k
0
- статистическим коэффициентом усиления
по математическому ожиданию; коэффициенты k
1
и k
2
- статистическими
коэффициентами усиления по случайным составляющим входных сигналов.
Значения коэффициентов статистической линеаризации определяют на
основе критериев вероятностной эквивалентности. Обычно используют два
критерия.
Первый критерий состоит в равенстве математических ожиданий и дис-
персий сигналов на выходе статистически линеаризованного и исходного
нелинейного звеньев. Для однозначной исходной нелинейности имеем:
dxxfxm
y
,
2
22
yyy
mdxxfxdxxfmxD
,
где f(x) - ПРВ сигнала X на входе нелинейного звена.

118
Математическое ожидание выходного сигнала линеаризованного звена
M[Y] равно
0
(или k
0
m
x
для нечетной нелинейности), а его дисперсия D[Y]
связана с дисперсией и среднеквадратическим отклонением входного сигнала
в соответствии с (4.15):
.][
22
1
2
1 xx
kDkYD
В результате получим:
dxxfx
0
или
dxxfx
m
k
x
1
0
, (4.19)
2
1
2
0
2
1
1
dxxfxk
x
. (4.20)
Знак в формуле (4.20) соответствует знаку производной
x
в точке,
соответствующей m
x
.
Второй критерий состоит в минимизации среднего квадрата ошибки ап-
проксимации выходного сигнала нелинейного звена выходным сигналом
линеаризованного звена:
min
10
2
2
10
2
,
kXkxM
.
Раскроем скобки в выражении для
2
и применим к нему первое необ-
ходимое условие экстремума по
0
и k
1
:
XkXkxxXkxM
1010
2
2
1
2
0
2
2
222
0
10
2
1
2
0
2
22
XxMkmDkxM
yx
,
022
0
0
2
y
m
,
02 2
1
1
2
XxMDk
k
x
.
Решение полученных уравнений дает выражения для определения
0
и
k
1
, доставляющих минимум
2
:

119
dxxfxm
y0
,
dxxfmxx
D
XxM
D
k
x
xx
11
1
. (4.21)
Отметим, что для
0
(и соответственно k
0
) оба критерия дают одинако-
вую расчетную формулу (4.19). Для k
1
получены различные расчетные
формулы. Поскольку оба критерия считаются равноценными, обычно реко-
мендуют вычислять k
1
как среднее арифметическое:
2
2
1
1
1
1
kk
k
,
где
1
1
k
- значение, получаемое на основе первого критерия по (4.20);
2
1
k
-
значение, получаемое на основе второго критерия по (4.21).
Для нелинейного звена с несколькими входами линеаризация произво-
дится в форме:
n
i
i
i
XkY
1
0
.
Здесь обычно ограничиваются использованием критерия минимума
среднего квадрата ошибки, дающего наиболее простые расчетные соотно-
шения:
min,...,,,,...,,
210
2
2
1
021
2
n
n
i
i
in
kkkXkxxxM
.
Повторим выполненную ранее процедуру:
n
i
i
i
n
i
n
j
n
i
i
i
j
j
i
i
XkXkXkXkM
11 1 1
00
2
0
22
222
n
i
n
i
i
iy
n
j
ji
ji
XMkmXXMkkM
1 1
0
1
2
0
2
22
,
022
0
0
2
y
m
,
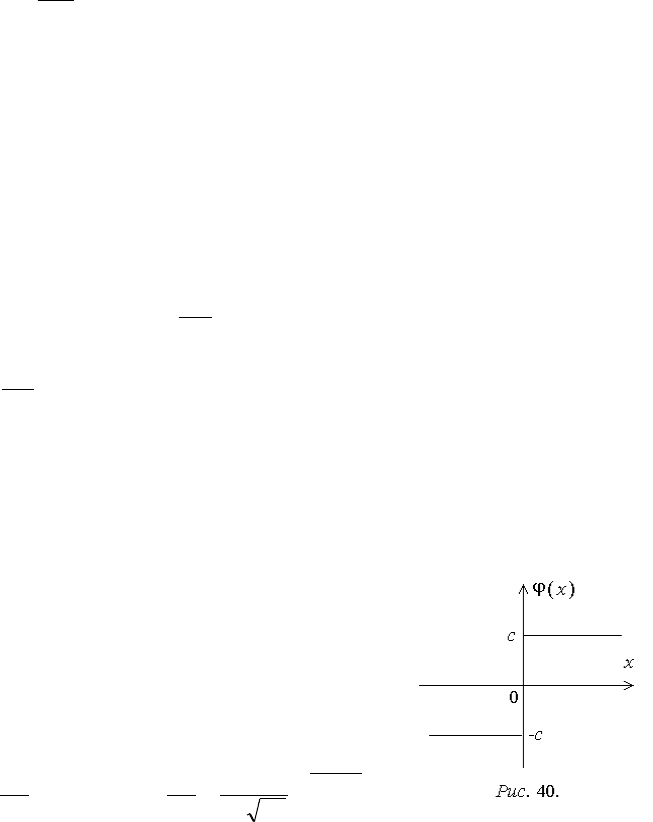
120
0,...,,22
21
1
2
i
n
n
j
ijj
i
XxxxMk
k
, i=1,2,...,n, (4.22)
где
ji
ij
XXM
- корреляционные моменты связи входных сигналов.
В результате средняя статистическая характеристика нелинейности оп-
ределяется как математическое ожидание сигнала на выходе звена:
0
= m
y
=M[(x
1
,x
2
,…,x
n
)],
а коэффициенты усиления по случайным составляющим входных сигналов
k
i
- из системы уравнений (4.22).
В частном случае при взаимно независимых входных сигналах звена (
ij
= 0 при i≠j) из (4.22) получаем:
i
n
x
i
XxxxM
D
k
i
,...,.
1
21
nnnxin
x
dxdxxfxfmxxxx
D
i
i
......,...,,...
1
11121
, i=1,2,...,n,
где D
xi
=
ii
.
Все полученные расчетные соотношения для определения коэффициен-
тов статистической линеаризации предусматривают использование ПРВ сиг-
налов на входе линеаризуемого звена. В силу допущения о наличии у линей-
ной части системы свойства фильтра, обычно используется ПРВ нормально-
го закона распределения. Рассмотрим некоторые
примеры.
Пример 1. Нелинейное звено (рис. 40) с иде-
альной релейной характеристикой (x)=csignx.
Линеаризация выполняется в форме
XkmkY
x 10
. Для определения k
0
применим
формулу (4.19):
dxe
xc
m
dxxfx
m
k
x
x
mx
x
xx
2
2
2
0
2
11 sign

121
0
2
2
2
1
2
dxe
m
c
x
x
mx
x
x
0
2
2
2
1
dxe
x
x
mx
x
x
x
x
x
m
u
m
u
x
duedue
m
c
22
22
2
,
где
x
x
mx
u
- стандартизованная нормальная величина. И далее:
0
2
0
2
0
2
0
2
0
2222
2
x
x
x
x
m
uu
m
uu
x
duedueduedue
m
c
k
x
x
xx
x
x
x
x
m
m
c
mm
m
c 2
5,05,0
,
где Ф(u) - интеграл вероятностей, рассмотренный в разд. 3.
Аналогично на основе (4.20), (4.21) можно получить:
2
1
2
2
1
22
0
2
2
1
1
41
2
1
2
2
x
x
x
x
mx
x
x
m
c
mkdxe
c
k
x
x
,
0
2
0
2
2
2
1
2
2
2
2
22
1
dxe
mxc
dxe
mxc
k
x
x
x
x
mx
x
x
mx
x
x
x
2
2
2
2
2
2
22
0
2
2
2
2
0
2
2
2
2
2
x
x
x
x
x
x
m
x
mx
x
x
mx
x
e
c
e
c
mx
de
c
.
Пример 2. Нелинейное звено имеет релейную характеристику с гистере-
зисом (рис. 41). Неоднозначную зависимость можно формально зам енить
однозначной:
,0иилипри
,0иилипри
),(
211
211
21
xbxbxc
xbс
xx
bx x
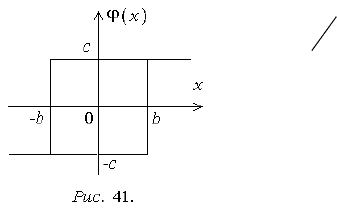
122
если рассматривать два входных сигнала: X
1
=X и
dt
dX
X
2
и использовать форму
2
2
1
10
XkXkY
.
Формулы для расчета коэффициентов ста-
тистической линеаризации типовых нелинейных
звеньев приводятся в справочных разделах [2, 32,
33].
Отметим в итоге, что коэффициенты стати-
стической линеаризации оказываются функциями
статистических характеристик входных сигналов нелинейного звена. Для
звена с одним входом
0
, k
0
и k
1
зависят от m
x
и σ
x
. Для звена с нескольки-
ми входами
0
и n коэффициентов k
i
зависят от вектора математических
ожиданий входных сигналов и матрицы моментов (4.12).
4.4. Расчет установившегося случайного процесса в нелинейной
стационарной системе
Замена нелинейного звена линеаризованной моделью позволяет ис-
пользовать принцип суперпозиции - провести раздельный анализ преобразо-
вания системой детерминированных и случайных составляющих входных
сигналов. Особенность применения принципа суперпозиции на основе ста-
тистической линеаризации состоит в том, что для случайных составляющих
нелинейное звено заменяется безынерционным звеном с коэффициентом
k
1
, а для детерминированных - безынерционным звеном с коэффициентом
k
0
(при нечетной нелинейности) или постоянным сигналом
0
.
Определяемые по (4.19)-(4.22) коэффициенты статистической линеари-
зации оказываются функциями моментов распределения сигналов на входе
нелинейности, которые, в свою очередь, вычисляются через передаточные
функции системы, включающей в себя линеаризованное звено, то есть зави-
сят от коэффициентов статистической линеаризации. Вследствие этого расчет
стационарного процесса в статистически линеаризованной системе сводится
к решению системы нелинейных алгебраических уравнений, требующему
применения численных методов.
Рассмотрим пример такого расчета для системы, структурная схема ко-
торой приведена на рис. 42, статическая характеристика нелинейного звена -
на рис. 40.
