Емельянов В.Ю. Методы моделирования стохастических систем управления

Подождите немного. Документ загружается.































3.6.2. Непараметрические методы восстановления закона распределения

Классические непараметрические методы восстановления закона рас-

пределения по случайной выборке x

,…,x

позволяют получить аппрок-

симации ПРВ или ФРВ кусочно-постоянными функциями.

Для аппроксимации ПРВ обычно используются статистические ряды

или гистограммы.

При построении статистического ряда выборка разбивается на разря-

ды:

j+1

], x

min

, x

j+1

+x, j=1,2,...,m; x

m+1

max

Количество разрядов m обычно выбирается в соответствии с условиями:

2015



при

500n

30m

при n>500.

Длина разряда постоянна:

minmax





. Разность x

max

-x

min

называ-

ется размахом выборки. Все попавшие в j-й разряд значения x далее счита-

ются одинаковыми и равными среднему значению для данного разряда v

Статистический ряд составляется в форме табл. 8.

Таблица 8

Статистический ряд

Номер

разряда

Границы разря-

да

Среднее зна-

чение

Число на-

блюдений

в разряде

Частота

разряда



…



j+1

…



m+1

Средние значения для разрядов определяются как средние арифметиче-

ские границ:

 

1





. Частоты разрядов - как отношения количест-

ва элементов выборки, попавших в данный разряд к общему объему выбор-

ки:





По статистическому ряду могут быть найдены оценки математического

ожидания и дисперсии случайной величины x:













jjx

vpvn

   













xjj

xjjx

mvpmvn

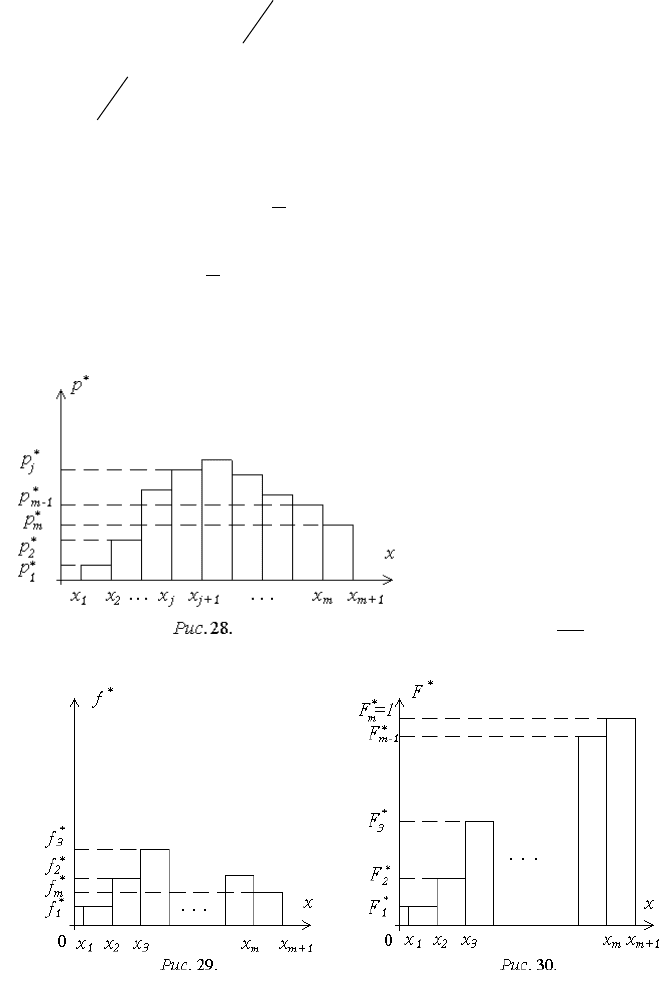
Гистограмма представляет собой графическую интерпретацию стати-

стического ряда (рис. 28).

На основе гистограммы

могут быть получены

аппроксимации ФРВ (рис.

29) или ПРВ (рис. 30). Ор-

динаты F

(x) и f

(x)

определяются по форму-

лам:















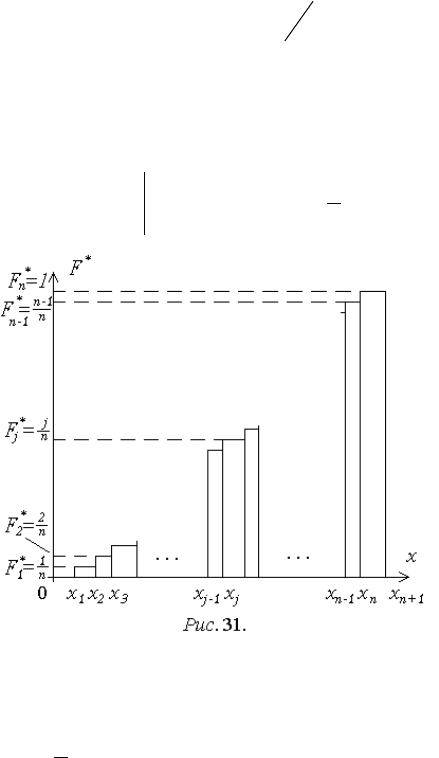
Более точной аппроксимацией выборочной ФРВ является статистиче-

ская функция распределения F

(x), определяемая как частота наблюдения

реализаций x

, не превышающих x:

 





, где n

- количество значе-

ний



Для ее построения вся выборка сортируется в порядке возрастания x:

xxxx  

. Теперь отношения порядковых номеров j к объ-

ему выборки n дают значение F

(x) для интервалов [x

j+1

] (рис. 31):

 

xxx











Менее наглядна, но более удобна для алгоритмической реализации иная

форма вычисления статистической функции распределения, не требующая

предварительной сортировки выборки:

   









, u

=x-x

 













.01

,00

при

Получаемые на основе рассмотренных методов оценки ПРВ и ФРВ на-

глядны и просты в реализации, но не обладают свойством достаточности.

В последнее время разработаны более эффективные оценки ПРВ, яв-

ляющиеся обобщениями "окошечной" оценки Розенблатта. Оценка Розенб-

латта имеет вид:

   













 













.10

,15,0

при

Величина 2h называется шириной окна. В общем случае она выбирается

в зависимости от объема выборки: h=h(n)>0, причем

 

0lim 



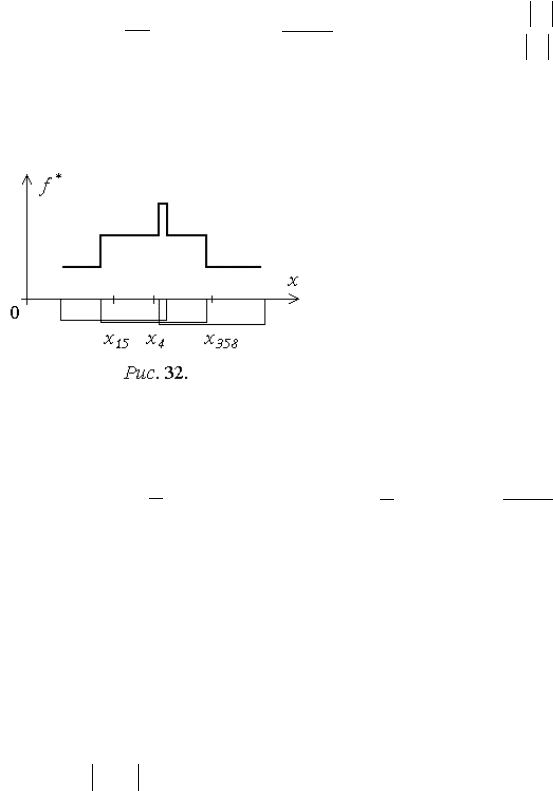
Принцип построения "око-

шечной" оценки состоит в том, что

с каждым выборочным значением

совмещается окно шириной 2h

(рис. 32). Значение оценки ПРВ для

любой точки пропорционально

количеству окон, накрывающих эту

точку.

Более общими и обладающи-

ми свойством достаточности явля-

ются ядерные оценки ПРВ вида

   









inn

xxK

   

iin

xxK

, 





Функция K

(x,x

) называется функцией ядра, h=h(n)>0 - коэффици-

ентом вклада. В отличие от оценки Розенблатта, здесь K(u) отличается от

нуля при любом u. Она имеет максимум при u=0 (x=x

), является четной

относительно u и монотонно убывает при удалении u от нуля. Благодаря

такому выбору функции ядра, для любой точки x обеспечивается определе-

ние оценки ПРВ с учетом степени удаленности от x каждого значения x

содержащегося в выборке.

Требования к K(u) и h(n):

 

uK

max

 

1







duuK

 

0lim 



uuK

 

0lim 



 





nnh

lim

Для конкретной задачи функция ядра и коэффициент вклада выбирают-

ся с учетом статистических характеристик обрабатываемой выборки [46].

Примеры функций ядра и коэффициентов вклада:

 

euK







 







 

euK





 





 nnh

где 

- оценка среднеквадратического отклонения.

3.7. Критерии согласия теоретического и выборочного законов

распределения

Восстановленный одним из рассмотренных способов выборочный за-

кон распределения нестабилен. После проведения дополнительной серии

опытов или повторения всего эксперимента в аналогичных условиях будет

получена другая случайная выборка, и все оценки могут измениться. Кроме

того, табличная или графическая форма закона распределения неудобны для

дальнейшего использования.

Поэтому обычно подбирают некоторый теоретический закон распреде-

ления вероятностей (аналитическое выражение для ПРВ или ФРВ), достаточ-

но близкий к выборочному, чтобы можно было рассматривать его как ап-

проксимацию истинного закона распределения исследуемой случайной

величины. Затем проверяют соответствие теоретического закона истинному

на основе критерия согласия теоретического и выборочного законов распре-

деления (проверка статистической гипотезы).

В соответствии с основными теоретическими положениями метода ста-

тистического моделирования по выборке конечного объема невозможно

оценить статистические характеристики случайной величины или процесса с

полной достоверностью. Поэтому вывод о согласии или несогласии теорети-

ческого и выборочного законов можно сделать только с некоторой вероят-

ностью. При этом следует учитывать две возможные причины обнаруженно-

го несогласия:

- неверный подбор теоретического закона;

- недостаточный объем выборки.

Процедура проверки статистической гипотезы с помощью критерия со-

гласия состоит в следующем:

- вычисляется значение некоторой меры расхождения подобранного

теоретического и выборочного законов распределения;

- оценивается вероятность того, что при данном числе опытов n и при

правильном подборе теоретического закона эта мера могла бы принять зна-

чение, большее или равное полученному.

Величина этой вероятности и является критерием согласия. Таким обра-

зом, критерий согласия - это вероятность того, что на основе выборки рас-

сматриваемого объема могло бы быть получено худшее соответствие теоре-

тического и выборочного законов.

Малая величина полученного критерия согласия свидетельствует о том,

что скорее всего теоретический закон распределения подобран неверно (ста-

тистическая гипотеза отвергается). При достаточно большой величине крите-

рия согласия нет оснований отвергать подобранный теоретический закон

(статистическая гипотеза принимается).

3.7.1. Критерий согласия Пирсона

Критерий согласия Пирсона, или критерий 

, наиболее удобен для

проверки соответствия теоретического закона распределения выборочному,

полученному в форме статистического ряда или гистограммы.

В качестве меры расхождения теоретического и выборочного законов

распределения используется величина

 

















npn

где n - объем выборки; m - количество разрядов; n

- число наблюдений в

разряде; p

- частота разряда; p

- вероятность попадания в j-й разряд

 

1



xxx

случайной величины x, распределенной по подобранному

теоретическому закону.

Вероятность

 

PP 

является функцией 



и числа степеней

свободы распределения 

: r=m-s-1, где s - количество параметров теоре-

тического закона, оценивавшихся по выборке. Например, для нормального

закона в общем случае s=2, а если m

или 

было заранее известно, s=1.

Аналитические зависимости для закона распределения 

известны, но на

практике удобнее пользоваться таблицами (при

50n

табл. 9).

Таблица 9

Распределение 

P=0,2

P=0,1

P=0,05

P=0,01

P=0,2

P=0,1

P=0,05

P=0,01

1,6

2,7

3,8

6,6

20,5

23,5

26,3

32,0

3,2

4,6

6,0

9,2

21,6

24,8

27,6

33,4

4,6

6,3

7,8

11,3

22,8

26,0

28,9

34,8

6,0

7,8

9,5

13,3

23,9

27,2

30,1

36,2

7,3

9,2

11,1

15,1

25,0

28,4

31,4

37,6

8,6

10,6

12,6

16,8

26,2

29,6

32,7

38,9

9,8

12,0

14,1

18,5

27,3

30,8

33,9

40,3

11,0

13,4

15,5

20,1

28,4

32,0

35,2

41,6

12,2

14,7

16,9

21,7

29,6

33,2

36,4

43,0

13,4

16,0

18,3

23,2

30,7

34,4

37,4

44,3

14,6

17,3

19,7

24,7

31,8

35,6

38,9

45,6

15,8

18,5

21,0

26,2

32,9

36,7

40,1

47,0

17,0

19,8

22,4

27,7

34,0

37,9

41,3

48,3

18,2

21,1

23,7

29,1

35,1

39,1

42,6

49,6

19,3

22,3

25,0

30,6

36,3

40,3

43,8

50,9

Вследствие случайности выборки при любом 



существует риск не-

обоснованно отвергнуть или принять то или иное теоретическое распределе-

ние. Жестких условий, безошибочно разграничивающих области согласия и

несогласия теоретического распределения с выборочным, сформулировать

невозможно. Поэтому правило принятия решения на основе критерия Пир-

сона имеет определенную степень гибкости, учитывающую риск получения

ошибки:

1. Определяется значение 



и в строке таблицы распределения 

, со-

ответствующей рассматриваемому r, находятся ближайшие к полученному





значения.

2. В верхней строке таблицы находится соответствующее значение P или

определяется диапазон, которому принадлежит значение P.

В зависимости от значения P принимается одно из возможных решений:

- при

01,0P

считается, что согласия между теоретическим и выбо-

рочным распределениями нет; теоретический закон отвергается и должен

быть заменен другим, подлежащим аналогичной проверке;

- при

1,0P

считается, что теоретическое распределение согласуется с

выборочным, то есть подобрано верно;

- при 0,01<P<0,1 считается, что согласие между теоретическим и вы-

борочным распределениями не обеспечивается скорее всего вследствие

недостаточного объема выборки; рекомендуется увеличить объем выборки

и повторить проверку в надежде на смещение значения P в другой интервал.

4. Если при 0,01<P<0,1 увеличение объема выборки невозможно или

не дает ожидаемого эффекта, с несколько большим риском принимается, что

границей областей согласия и несогласия теоретического и выборочного

законов является P=0,05.

3.7.2. Критерий согласия Колмогорова

Критерий согласия Колмогорова наиболее удобен в том случае когда по

случайной выборке восстановлена статистическая функция распределения

(x). В качестве меры расхождения здесь рассматривается максимум абсо-

лютной величины разности теоретической и выборочной (статистической)

ФРВ:

   

xFxF



 max

где F(x) - теоретическая ФРВ.

Критерием согласия является вероятность того, что случайная величина

n

при данном объеме выборки n и правильном выборе теоретиче-

ского закона могла бы принять значение, не меньшее



 



















PnP

. (3.30)

При

50n

вероятности (3.30) рассчитываются в соответствии с зако-

ном распределения Колмогорова. Наиболее важные для практики их значе-

ния представлены в табл. 10.

Таблица 10

Распределение Колмогорова



1,0

1,1

1,2

1,3

1,4

1,5

1,6

1,7

1,8

1,9

0,270

0,178

0,112

0,068

0,040

0,022

0,012

0,006

0,003

0,002

Если теоретический закон распределения подобран, порядок примене-

ния критерия Колмогорова аналогичен рассмотренному выше для критерия

Пирсона.

Однако чаще всего критерий Колмогорова применяют непосредственно

для подбора теоретического закона распределения, задавшись некоторым

критическим значением P=

(уровнем значимости), опре-

деляющим границу области

согласия теоретического и

выборочного законов (допус-

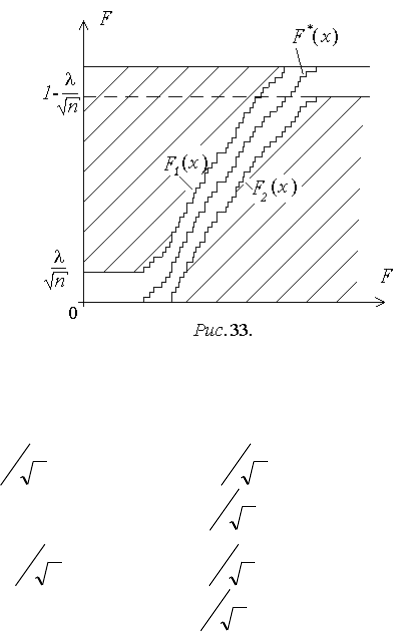
тимой области). В этом случае

для выбранного значения  по

табл. 10 находят соответст-

вующее значение  и на осно-

ве графика F

(x) строят допус-

тимую область (рис. 33). Огра-

ничивающие ее кривые F

(x)

и F

(x) определяются сле-

дующими соотношениями:

 

   

 





























,11

при

 

   

 





























при

Любой теоретический закон распределения, график ФРВ которого не

выходит за пределы области между кривыми F

(x) и F

(x), то есть при лю-

бом значении x удовлетворяющий неравенству

     

xFxFxF



, счита-

ется согласующимся с результатами эксперимента. Обычно используют

значения 0,1 и соответственно 1,22.

3.7.3. Другие задачи проверки статистических гип отез, виды критериев и

их характеристики

Рассмотренная выше задача проверки соответствия теоретического и

выборочного законов распределения относится только к одному из видов

задач проверки статистических гипотез [5, 20, 35, 43, 46]. Рассмотрим еще два

часто встречающихся на практике вида подобных задач.

Задача статистической проверки параметрической гипотезы возникает,

когда известен закон распределения исследуемой случайной величины F(x),

но неизвестен один из его параметров . Основная (нулевая) параметриче-

ская гипотеза, обозначаемая как H, состоит в утверждении, что данный па-

раметр имеет определенное значение: 

По случайной выборке x

,…,x

находят несмещенную состоятель-

ную оценку 

параметра и устанавливают, значимо или незначимо (до-

пустимо) различие между 

и 

. Для проверки используют статистиче-

ский критерий W - соответствующим образом подобранную случайную

величину, зависящую от 

. Закон распределения W определяют исходя из

условия, что элементы выборки являются независимыми случайными вели-

чинами, законы распределения которых совпадают с F(x) при 

, то есть

из условия выполнения гипотезы H.

Выбирают значение уровня значимости  (обычно, в пределах от 0,01 до

0,05), и интервал возможных значений W разбивают на две области - допус-

тимую 

и критическую 

в соответствии с условием

P(W

H)=. (3.31)

Находят расчетное значение статистического критерия w

=W(

), соот-

ветствующее используемой выборке. Гипотеза H принимается, если



, и отвергается в противоположном случае.

Как уже отмечалось выше, из-за ограниченного объема случайной вы-

борки при использовании статистических критериев всегда имеет место риск

получения неверных выводов. Возможны два варианта ошибки:

- отвергается правильная гипотеза (ошибка первого рода);

- принимается неправильная гипотеза (ошибка второго рода).

Как видно из (3.31), уровень значимости  представляет собой вероят-

ность ошибки первого рода. Для определения вероятности ошибки второго