Эддоус М., Стэнсфилд Р. Методы принятия решений

Подождите немного. Документ загружается.

Поэтому

Гл.

Вероятностные распределения

68^

е"^'^

Р(2 неполадки в день) = —'—rj = 0,1171.

О Пример 2.9. В компании, сдающей на прокат две машины, каждодневный

спрос на автомобили подчиняется распределению Пуассона и в среднем составляет

1,3 машины в день. Предположим, машины используются в равной степени.

Какова вероятность, что в любой из дней:

1) ни на одну машину не будет заказов;

2) одна из машин совершенно точно будет арендована, а другая — то ли

будет, то ли нет;

3) на обе поступят заказы.

Решение.

Число заказов на машину в день — это дискретная величина. Вероятность г

заказов такова:

Р(г)=^"^^^ . г = 0,1,2.3,...

Р(нет заказов на машины) = Р(спрос за день равен 0):

Р<г = 0)

-bi^^—

0,2725

Р(ни один автомобиль не заказан) = Р(спрос на одну из машин

или 1, а

на другую

—

Р(г = 0) + Р(г = 1)

Р(другая машина арендована) =

0,2725

+ ^'^^^

i = 0,4497.

Примечание: Р(другая машина арендована)°=1/2, так как машины используются

в равной степени.

Р(обе машины арендованы) = Р(спрос в день ^ 2) =

= 1- P(rS 2)*

= 1- {P(r = 0)+P(r=l)}=r

= 1- 0,6268=0,3732.

2.42.

Математическое озювдание

дисперсия распределения Пуассона

Математическое ожидание (или среднее число "успехов" на каком-то интервале)

может быть определено по данным конкретной ситуации. Если найдено математи-

ческое ожидание, то и дисперсия известна, так как одно из свойств распределения

вероятностей Пуассона состоит в следующем:

Ч. 1. Принятие решений в условиях

недостатка

информации

Математическое ожидание = Дисперсия.

Отсюда стандартное отклонение числа "успехов" на интервале равно:

Стандартное отклонение = VДисперсия =

Математическое ожидание .

Это свойство полезно в тех случаях, когда имеются данные о случайной

величине и требуется узнать, применимо или нет распределение Пуассона.

2.5. РАСПРЕДЕЛЕНИЕ ПУАССОНА КАК АППРОКСИМАЦИЯ

БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ

При определенных обстоятельствах распределение Пуассона может быть исполь-

зовано как замена биномиального распределения. Как, например, в примере 2.6 ,

где расчеты могут отнять много времени при использовании биномиального рас-

пределения. Если же условия позволяют, то расчеты можно произвести, восполь-

зовавшись распределением Пуассона. Тогда гораздо легче мы получим почти тот

же результат. Аппроксимация биномиального распределения Пуассона дает хоро-

шие результаты, если имеются:

Большое количество опытов; т.е. п

—

большое, предпочтительно п i. 30;

Малая вероятность "успеха" в каждом опыте; т.е. р — маленькое,

предпочтительно р ^ 0,10;

Предполагаемое количество "успехов" меньше пяти; т.е. пр ^ 5.

В этих обстоятельствах распределение Пуассона со средним m=pn вполне

может бьпь использовано вместо биномиального распределения. Чем больше п и

меньше р, тем точнее результат. В § 2.8 мы рассмотрим пример, как поступать с

биномиальными расчетами при большом р. В этом случае для замены может быть

использовано нормальное распределение.

О Пример 2.10. Производители карманных калькуляторов знают из опыта

работы, что 1% произведенных и проданных калькуляторов имеют дефекты и их

должны заменить по гарантии. Большая аудиторская фирма купила 500 кальку-

ляторов. Какова вероятность, что пять или больше калькуляторов нужно будет

заменить?

Решение.

Ситуация прекрасно укладывается в рамки биномиального распределения:

п =

500,

р =

0,01,

q =

0,99,

пр

Так как п — большое, р — маленькое, а пр — меньше или равно пяти, то в

качестве замены биномиального распределения может быть использовано распре-

деление Пуассона.

а) Расчеты с использованием биномиального распределения, вероятности г

дефектов в выборке дали следующие результаты:

Р(г)

^С,хО,01'х0.99*"-''; г=0. 1,2 500;

Гл.

2. Вероятностные распределения 55

Р (г г 5) =

- Р (г S 5) =

- (Р (г = 0) + Р

(г

= t) + Р (г

2) + Р(г = 3) + Р

(г

= 4)|;

P(0) = 0.01<'x0.99»•x^g^^ = 0,99»» =0,00657;

Р (1) = 0,01'

0,99^*

^^^ = 0,01

0,99** х 500 = 0,03318;

Р (2) = 0,01^

0,99**'

^ = 0,01^

0,99**' х ^^^^ = 0.08363;

Р (3) = 0.01'

0.99*'" к -Ш- = 0,01'

0.99*»' х 500

»<

499 х 498 ^ ^

^^^^З;"

43/1 J1 3x2x1

Р (4) = 0,01* х 0,99**'

^^ = 0.01* х 0.99**' х 500x499x498x497 ^

4Эо1 41 4x3x2x1

Всего 0,43961.

Отсюда

Р(г г 5) = 1 - {0,43961} =

О,

56039

(до пяти знаков после запятой),

Вероятность, что придется заменять 5 или больше калькуляторов,равна

0,560

(до трех знаков после запятой).

б) Расчеты с использованием распределения Пуассона:

m = пр = 500 х 0,01 = 5.

Вероятность г бракованных изделий в выборке приблизительно равна:

Р(г) = ^, г = 0, 1,2,3, ....

Отсюда

Р (г ^ 5) =

- |Р

(г

= 0) + Р

(г =

1) + Р (г » 2) + Р

(г

- 3) + Р (г = 4)

Р (0) = с"' =0,00674;

Р (1) = е~* х 5' - Р (0)

5 = 0,03369;

Р (2)

е"'

Ij-

- Р

(1) X

I =

0,08422;

^ 5' 5

P(3)»e-'x|i^ = P(2)x| =0,14037;

S6 Ч. 1. Принятие решений в условиях

недостатка информации

Р (4) = е"^

Р (3)

7 = 0,17547;

41 4

Всего: 0,44049.

Отсюда

Р(г г 5) =

- 0,44049 = 0,55951

(до пяти знаков после запятой).

Вероятность, что 5 или больше калькуляторов придется заменить, равна

0,560

(до трех знаков после запятой). С такой точностью результат совпадает с тем, что

мы получили в пункте (а), используя биномиальное распределение.

2.6. РАСПРЕДЕЛЕНИЕ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ

ВЕЛИЧИНЫ

2.6.1.

Непрерывная случайная величина и плотность ее Еюроятности

В предыдущих параграфах этой главы мы рассмотрели вероятностное распределе-

ние дискретной случайной величины. Остальные разделы посвящены равномерно-

му и нормальному распределению непрерывных случайных величин. Если в ходе

эксперимента все значения случайной величины оказываются на определенном

замкнутом участке и могут принимать в нем любые значения, то значит мы имеем

дело с непрерывной случайной величиной. Непрерывная случайная величина

имеет специфику в распределении вероятностей.

Например, если измерить объемы производимых заводом пластмассовых буты-

лок для сока, которые должны быть равны 200 мл, то полученные цифры

окажутся на каком-то определенном интервале, допустим, от 190 до 210 мл. В

данном случае непрерывная случайная величина будет иметь неограниченное

множество значений в этих пределах. Получим функцию распределения вероят-

ностей для непрерывной случайной величины. Предположим, мы имеем непрерыв-

ную случайную величину X, которая принимает значение х в интервале Х) и

Х2

для которого функция вероятности является непрерывной, то функция распреде-

ления непрерывной случайной величины равна f(x), Xj < х < Х2.

График функции распределения непрерывной сл)^айной величины представ-

ляет собой кривую, в отличие от линейной диаграммы для распределения дискрет-

ной случайной величины.

О Пример 2.11.

а) Функция распределения:

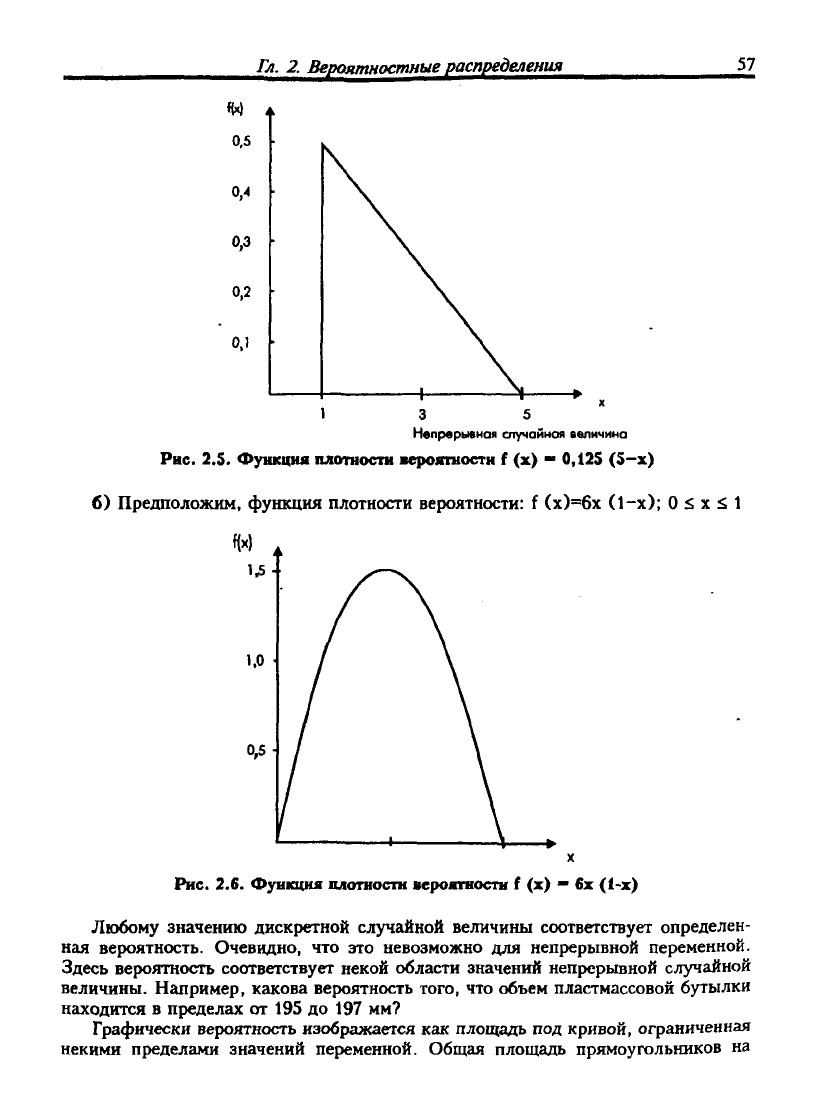
f (х) = 0,125 (5-х) для 1<х<5.

График распределения вероятностей для заданной функции будет иметь вид

(рис.

2.5.):

Гл.

Вероятностные распределения

3 5

Непрерывная случайная авличина

Рис.

2.S. Функция плотности вероятности f (х) •• 0,12S (S-x)

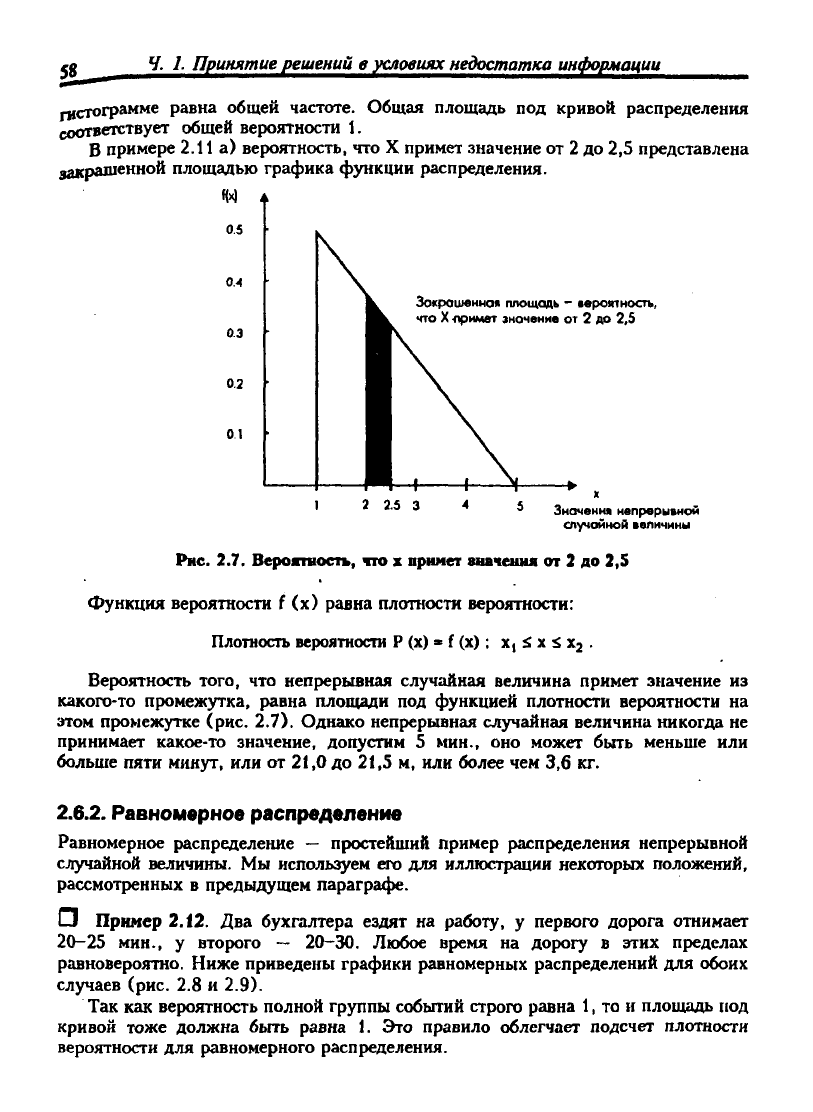
б) Предположим, функция плотности вероятности: f (х)=6х (1-х);

S х 5 1

Рис.

2.6. Функция алотностн вероятности f (х) - 6х (1-х)

Любому значению дискретной случайной величины соответствует определен-

ная вероятность. Очевидно, что это невозможно для непрерывной переменной.

Здесь вероятность соответствует некой области значений непрерывной случайной

величины. Например, какова верюятность того, что объем пластмассовой бутылки

находится в пределах от 195 до 197 мм?

Графически верюятность изобр)ажается как площадь под кривой, ограниченная

некими пределами значений переменной. Общая площадь прямоугольников на

58_

Ч. 1. Принятие решений в условиях недостатка информации

хястограмме равна общей частоте. Общая площадь под кривой распределения

соответствует общей вероятности 1.

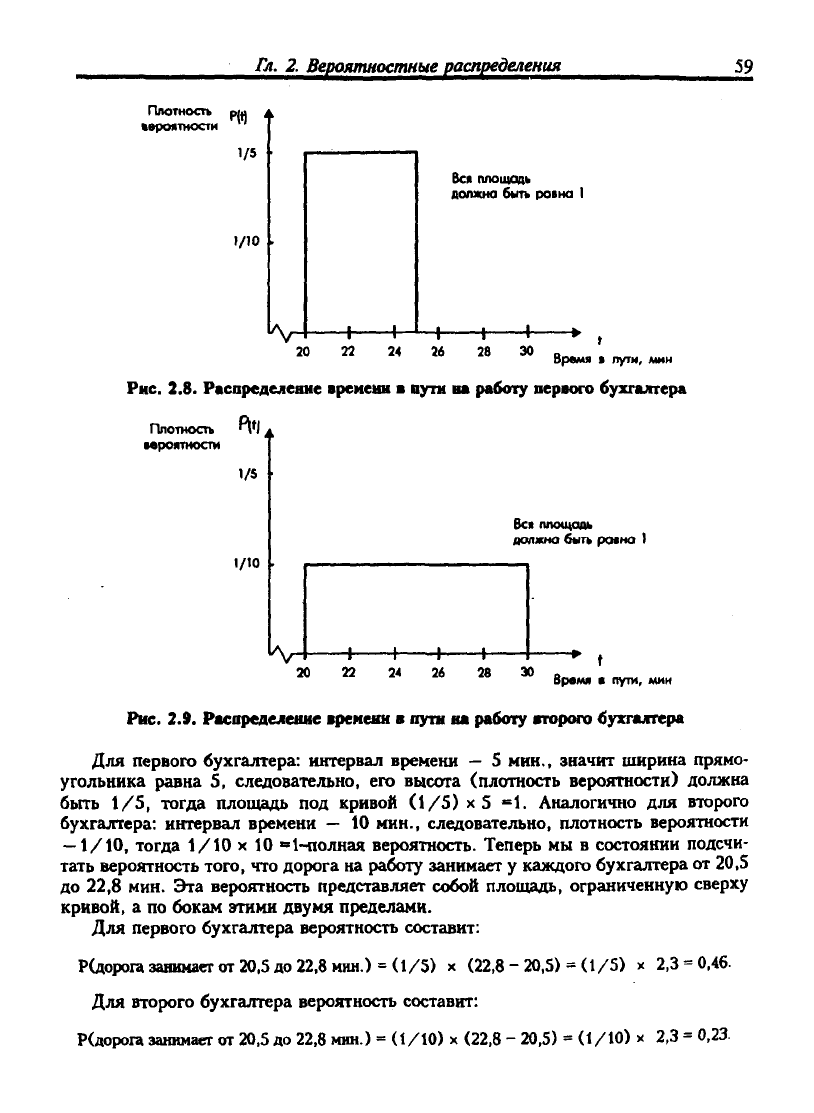
В примере 2.11 а) вероятность, что X примет значение от 2 до 2,5 представлена

закрашенной площадью графика функции распределения.

4x1

0.5

ол

0.3

0.2

Зокрошвмная площадь - •ероятностъ,

что X -примет зноченив от 2 до 2,5

Значения непрврыямой

случайной яеличины

Рис. 2.7. Вероятность, что х примет «начения от 2 до 2,5

Функция вероятности f (х) равна плотности вероятности:

Плотность вероятности Р (х)» f (х) ;

й х i

Х2

•

Вероятность того, что непрерывная случайная величина примет значение из

какого-то промежутка, равна площади под функцией плотности вероятности на

этом промежутке (рис. 2.7). Однако непрерывная случайная величина никогда не

принимает какое-то значение, допустим 5 мин., оно может быть меньше или

больше пяти минут, или от 21,0 до 21,5 м, или более чем 3,6 кг.

2.6.2.

Равномерное распределение

Равномерное распределение — простейший пример распределения непрерывной

случайной величины. Мы исполь^ем его для иллюстрации некоторых положений,

рассмотренных в предыдущем параграфе.

LJ Пример 2.12. Два бухгалтера ездят на работу, у первого дорога отнимает

20-25 мин., у второго — 20-30. Любое время на дорогу в этих пределах

равновероятно. Ниже приведены графики равномерных распределений для обоих

случаев (рис. 2.8 и 2.9).

Так как вероятность полной группы событий строго равна 1, то и площадь иод

кривой тоже должна бьггь равна 1. Это правило облегчает подсчет плотности

вероятности для равномерного распределения.

Гл.

Вероятностные распределения

Плотность

квроятиости

1/5

•

1/10

Вся площопь

должна 6wTk ровна

Время

•

пути,

мин

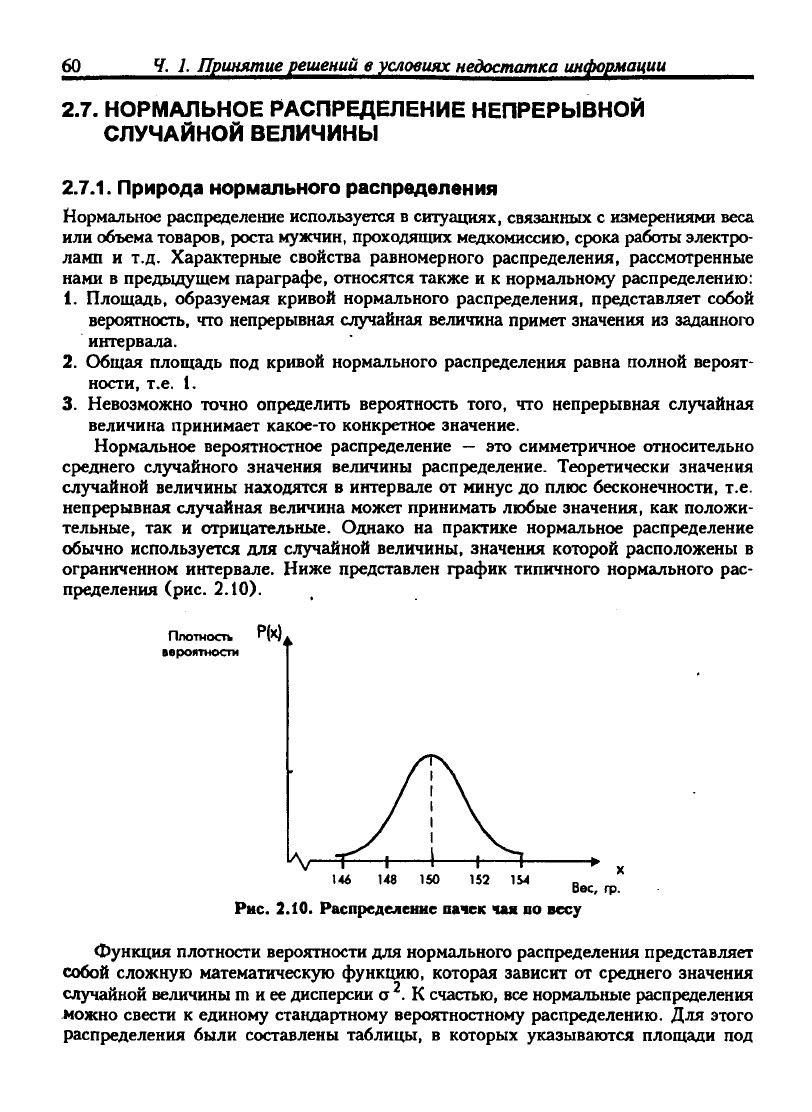
Рис. 2.8. Распределение вреиенн в пути вв работу первого бухгалтера

Плотность

мроятиости

1/S

Вся ппо«цадь

должна быть раяно I

I/IO

Время

лути,

мни

Рис. 2.9. Рвспредедение времени в пути на работу второго бухгалтера

Для первого бухгалтера: интервал времени —

мин., значит ширина прямо-

угольника равна

следовательно,

его

высота (плотность вероятности) должна

бьггь

1/5,

тогда площадь

под

кривой

(1/5) х 5 =1.

Аналогично

для

второго

бухгалтера: интервал времени —

мин., следовательно, плотность вероятности

—

1/10, тогда

1/10

=1-полная вероятность. Теперь мы

состоянии подсчи-

тать вероятность того, что дорога на работу занимает

каждого бухгалтера от 20.5

до 22,8 мин. Эта вероятность представляет собой площадь, ограниченную сверху

кривой,

по бокам этими двумя пределами.

Для первого бухгалтера вероятность составит:

РСчорога занимает от 20.5 до 22,8 мин.) = (1/5)

(22.8

20,5)

(1/5)

2,3 = 0,46.

Для второго бухгалтера вероятность составит:

Р(дорога занимает от 20.5 до 22.8 мин.)

(1/10)

(22,8

20,5)

(1/10)

2,3 = 0,23.

60 Ч. 1. Принятие

решений

в условиях

недостатка информации

2.7.

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ НЕПРЕРЫВНОЙ

СЛУЧАЙНОЙ ВЕЛИЧИНЫ

2.7.1.

Природа нормального распределения

Нормальное распределение используется в ситуациях, связанных с измерениями веса

или объема товаров, роста мужчин, проходящих медкомиссию, срока работы электро-

ламп и т.д. Характерные свойства равномерного распределения, рассмотренные

нами в предыдущем параграфе, относятся также и к нормальному распределению:

Площадь, образуемая кривой нормального распределения, представляет собой

вероятность, что непрерывная случайная величина примет значения из заданного

интервала.

Общая площадь под кривой нормального распределения равна полной вероят-

ности, т.е. 1.

Невозможно точно определить вероятность того, что непрерывная случайная

величина принимает какое-то конкретное значение.

Нормальное вероятностное распределение — это симметричное относительно

среднего случайного значения величины распределение. Теоретически значения

случайной величины находятся в интервале от минус до плюс бесконечности, т.е.

непрерывная случайная величина может принимать любые значения, как положи-

тельные, так и отрицательные. Однако на практике нормальное распределение

обычно используется для случайной величины, значения которой расположены в

ограниченном интервале. Ниже представлен график типичного нормального рас-

пределения (рис. 2.10).

Плотность

вероятностм

\и 148 150 152 154 о "*

Вес, ф.

Рис.

2.10. Распределение пачек чая по весу

Функция плотности вероятности для нормального распределения представляет

собой сложную математическую функцию, которая зависит от среднего значения

случайной величины m и ее дисперсии а . К счастью, все нормальные распр)еделения

можно свести к единому стандартному вероятностному распределению. Для этого

распределения были составлены таблицы, в которых указываются площади под

Гл.

Вероятностные распределения

кривой для различных значений непрерывной случайной величины и по которым

мы можем определить ту вероятность, которая нам требуется.

В стандартном нормальном распределении среднее значение случайной вели-

чины равно

О,

дисперсия равна

и, следовательно, стандартное отклонение равно 1.

Замена нормального распределения стандартным распределением означает то, что

значения случайной величины (минуты, грам»п>1, сантиметры и т.д.) выражены

стандартным отклонением среднего значения случайной величины. После замены

реальных цифр единицами стандартного отклонения (z) требуемые вероятности

могут быть найдены по таблице.

Существует несколько вариантов таблиц нормального распределения. Все они

дают один и тот же результат, только несколько различными путями. В Приложе-

нии 2 представлены таблицы вероятностей случайной величины, значения которой

на

стандартных отклонений выше среднего.

2.7.2.

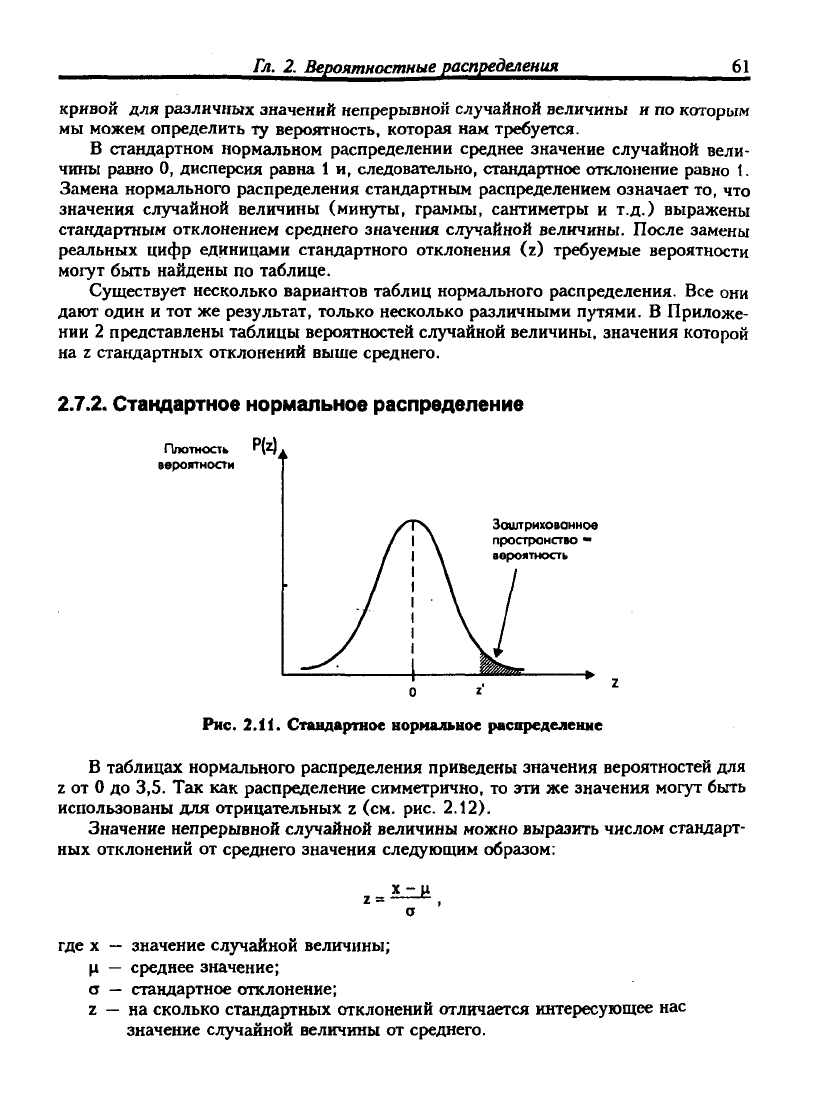
Стандартное нормальное распределение

Р(4л

Плотность

вероятности

Заштрихованное

простронство ~

вероятность

Рис.

2.11. Стандартное нормальное распределение

В таблицах нормального распределения приведены значения вероятностей для

от

до 3,5. Так как распределение симметрично, то эти же значения могут быть

использованы для отрицательных z (см. рис. 2.12).

Значение непрерывной случайной величины можно выразить числом стандарт-

ных отклонений от среднего значения следующим образом:

где

X —

значение случайной величины;

—

среднее значение;

—

стандартное отклонение;

—

на сколько стандартных отклонений отличается интересующее нас

значение случайной величины от среднего.

Ч. 1.

Принятие решений

условиях недостатка информации

Плотность

P(z)

•ероятности

Заштрихованное лростронспо •

вероятность

•г О f

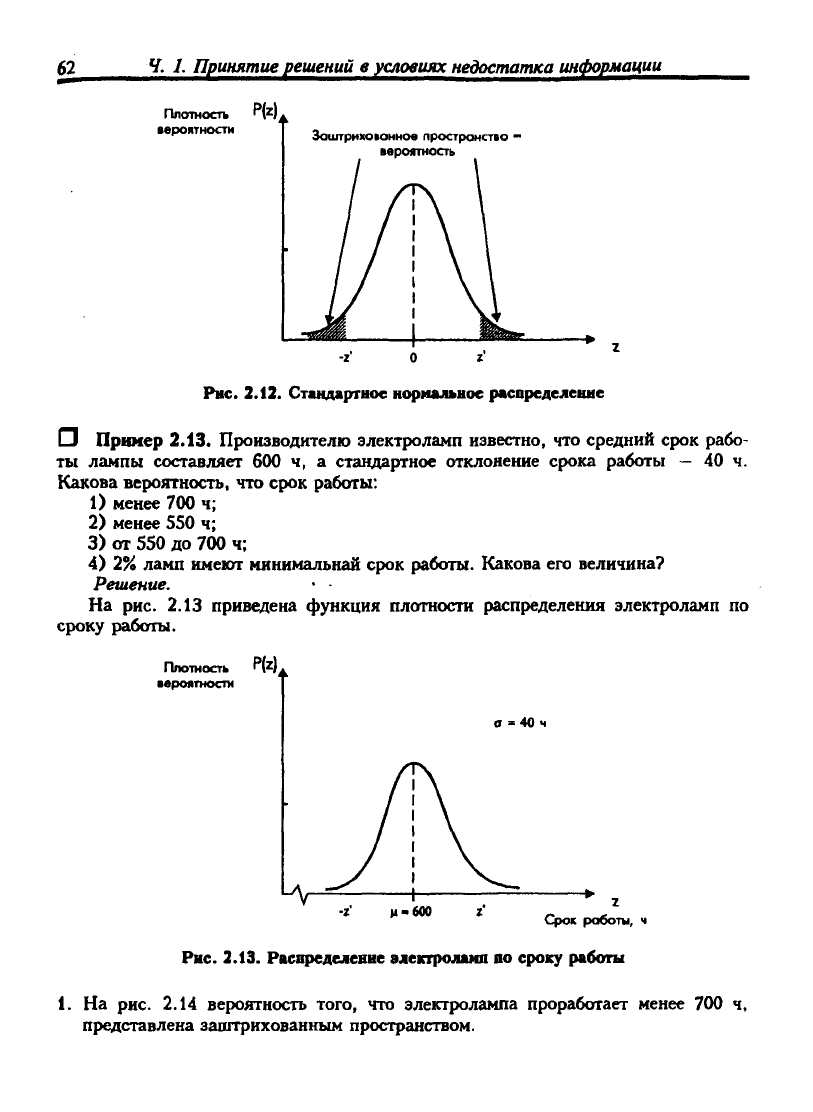
Рис. 2.12. Стандартное нормальное распределение

Ы Пример 2.13. Производителю электроламп известно, что средний срок рабо-

ты лампы составляет 600 ч, а стандартное отклонение срока работы — 40 ч.

Какова вероятность, что срок работы:

1) менее 700 ч;

2) менее 550 ч;

3) от 550 до 700 ч;

ламп имеют минимальнай срок работы. Какова его величина?

Решение.

На рис. 2.13 приведена функция плотности распределения электроламп по

сроку работы.

Плотность

•ароятностм

М-600

Срок работы, ч

Рис. 2.13. Распределение алектролаип по сроку работы

На рис. 2.14 вероятность того, что электролампа проработает менее 700 ч,

представлена заштрихованным пространством.