Эддоус М., Стэнсфилд Р. Методы принятия решений

Подождите немного. Документ загружается.

Гл.

2. Вероятностные распределения 43

Среднее значение, основанное на вероятностном распределении, называется

обычно математическим ожиданием (при условии многократного проведения

эксперимента). Математическое ожидание дискретной случайной величины обо-

значается Е(г) или ц.

Так как ]^ Р (г) = 1, то математическое ожидание имеет вид:

E(r) = X;rP(r).

Вариация вероятностного распределения может быть измерена при помощи

среднего квадратического отклонения или дисперсии дискретной случайной

величины:

Дисперсия =

(Стандартное отклонение)

А так как J] Р (г) = 1:

o2-2;i^P(r)-{E(r))2.

Пример 2.3. Бросаем монету три раза и регистрируем число «решек».

Возможные исходы:

{ррр,

рро, pop, орр, роо, оро, оор, ооо}

Дискретная случайная величина

—

количество «решек», ее возможные значения:

г =

или 1 или 2 или 3 .

Вероятностное распределение, основанное на значениях возможных исходов,

следующее (табл. 2.5):

Таблица 2.S. Распределение аероялюстей «решек»'

Число

4решек*;

Р(г)

t 2 3

1/8 3/8 3/8

1/8

Математическое ожидание «решек»:

(г) = 21 г Р

(г)

(О X

1/8) +

(1 X

3/8) + (2

3/8) + (3

1/8) = 12/8

1,5.

Дисперсия «решек»:

о^

2]г^

Р (г) - (Е

(г))^

(О

х1/8 +

1 X

3/8 + 4

3/В + 9

1/8) -

1,5^

3,0 - 2,25 » 0,75.

Стандартное отклонение числа «решек»

а - V^J5 - 0,87.

Ч. 1. Принятие решений в условиях

недостатка

информации

2.3.

БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

2.3.1.

Что такое биномиальное распределение

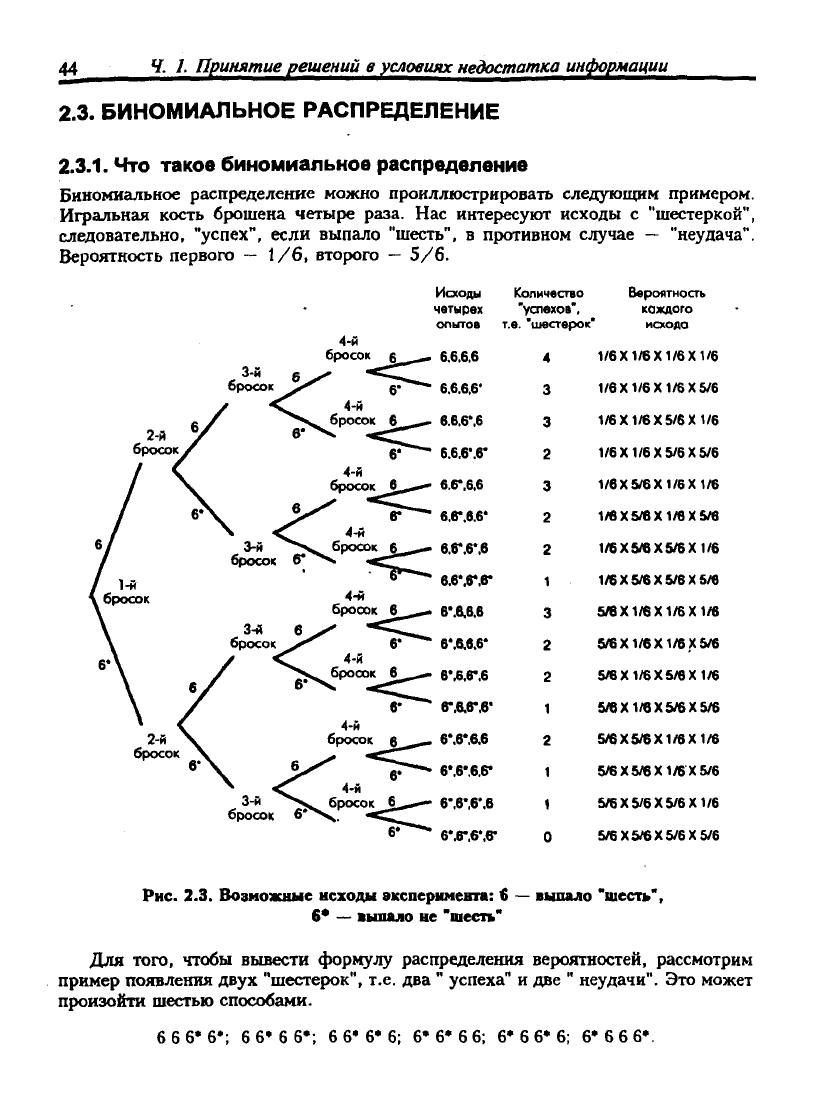
Биномиальное распределение можно проиллюстрировать следующим примером.

Игральная кость брошена четыре раза. Нас интересуют исходы с "шестеркой",

следовательно, "успех", если выпало "шесть", в противном случае — "неудача".

Вероятность первого

—

1/6, второго

—

5/6.

Количество

'успехов",

т.е.

"шестерок"

Вероятность

каждого

исходе

1/6X1/6X1/6X1/6

1/6X1/6X1/6X5/6

1/6X1/6X5/6X1/6

1/6X1/6X5/6X5/6

1/6X5/6X1/6X1/6

1/6X5/6X1/6X5/6

1/6X54X5/6X1/6

1/6X5/6X5/6X5/6

5/6X1/6X1/6X1/6

5/6X1/6X1/6X5/6

5/6X1/6X5/6X1/6

5/6X1/8X5/6X5/6

S/6XS/6X1/6X1/6

5/6X5/6X1/6X5/6

5/6X5/6X5/6X1/6

5/6X5/6X5/6X5/6

Рис.

2.3. Возможные исходы эксперимента: 6

—

выпало "шесть",

—

выпало не 'шесть'

Для того, чтобы вывести формулу распределения вероятностей, рассмотрим

пример появления двух "шестерок", т.е. два " успеха" и две " неудачи". Это может

произойти шестью способами.

6 6

6*; 6 6» 6 б»; 6

6* 6; 6* 6* 6

6* 6

6; 6* 6 6 6».

Гл.

Вероятностные распределения

Вероятности этих исходов равны:

б''б''бЧ

6 6 •

Отсюда вероятность появления двух "шестерок"

— 1

х1—

% (количество возможнглх способов получения

двух'шестерок'

при

четырех бросках)

Р( две

'шестерки'

при четырех бросках)

=гг! х-^ х6

= -

\Ъ) \Ъ) 1296 •

Для иллюстрации вероятностей остальных исходов воспользуемся схемой;

nz-n- " ^ л f^'f f^)* 4 625

Р (О шестерок при четырех бросках) = д '*R Х1 =

в) [6) 1296 •

пп-

" А •» r^V fsf .. 500

Р (1 шестерка при четырех бросках) = ^

Гс ^ *

Т^ос !

nz-o"

" < ч flf fsf с 150

Р (2 шестерки при четырех бросках) =\-^\ х ^ х 6 =

.;.„•.

;

(о) (о) 1хУо

Р (3 "шестерки" при четырех бросках) =\-^\ х

о'

if Г5У . 20

х4 =

1296 '

riV rsf 1

Р (4 "шестерки" при четырех бросках) = т х|

[6) [6) 1296 •

тт '296 ,

Полная вероятность = .„-ц. = 1.

I2in)

Отсюда можно вывести формулу, описывающую вероятность появления "шес-

терки" при четырех бросках:

riY rsf""

Р (г "шестерок" при четырех бросках) = гт х гё ^ (число опытов с г

I о1

1оI

"шестерками").

46 Ч. 1. Принятие решений в условиях

недостатка

информации

Из главы 1 известно, что число "успехов" г при четырех попытках представ-

ляет собой число комбинаций г элементов из четырех элементов, т.е.:

4^ 41

' г! (4 -

г)!

Отсюда:

Р (г "шестерок" при четырех бросках) =

д 1

х г?! х *^г

•

Важные характеристики этого биномиального эксперимента:

Все четыре опьгга абсолютно идентичны.

Результаты опыта друг от друга не зависят.

Для каждого опыта возможны два исхода: 6 и не 6

—

"успех" и "неудача".

Для каждого опыта вероятность "успеха" одинакова

—

1/6.

Эти характеристики являются необходимым условием биномиального распре-

деления. Теперь от конкретного эксперимента перейти к общей формуле.

2.3.2.

Биномиальное распределение

В любом эксперименте, где для п идентичных, независимых опытов с двумя

возможными исходами ("успех" и "неудача") вероятность "успеха" одна и та же,

вероятность г "успехов" в о опытах равна:

Р (г) = (вероятность г "успехов") х (вероятность (п-г) "неудач") х

(число способов, которыми

это

может быть сделано)

^<'>»Й1^'''''""

г = 0,1.2....„,

где р

—

вероятность "успеха" в очередном опыте;

q — вероятность "неудачи" р + q = 1-

О Пример 2.4. Вероятность поломки одного из пяти работающих независимо

друг от друга станков равна 0,2. Если происходит поломка, станок до конца дня не

работает. Какова вероятность, что 0,1,2, 3, 4, 5 станков сломаются в течение дня?

Решение.

В данном случае присутствуют все условия биномиального распределения:

Пять станков представляют собой пять идентичных опытов.

Станки работают независимо друг от друга.

Возможны два исхода для каждого из станков

—

или он ломается или нет.

Вероятность поломки одинакова

—

0,2.

Следовательно, вероятность бесперебойной работы равна 0,8, отсюда вероят-

ность г поломок в течение дня:

Р (г) =

^С,

(0,2)' (0,8)5 -г J ^ о 1 5.

Гл.

2. Вероятностные распределения

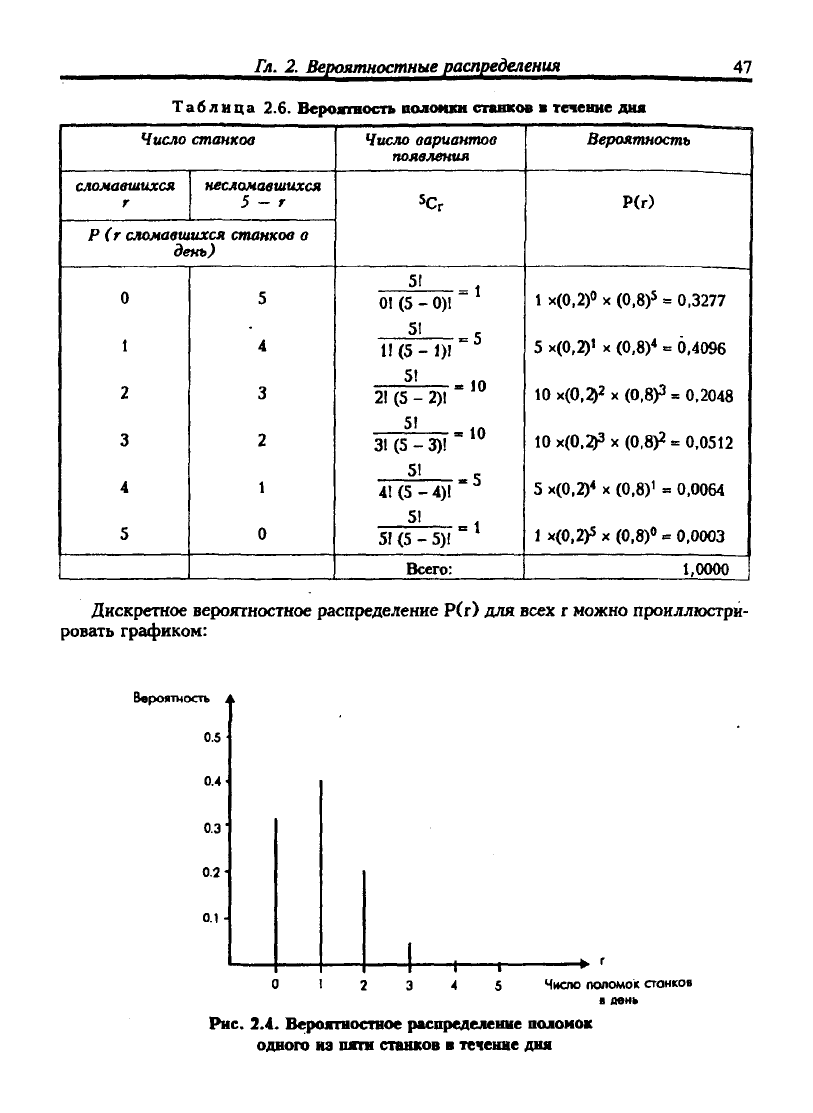
Таблица 2.6. Вероятность полоикн станков в течение дня

Число станков

Число вариантов

появления

Вероятность

сломавшихся

несломавшихся

5 - г

5Сг

Р(г)

Р (г

сломавшихся станков

день)

01(5-

11(5-

21(5-

31(5-

41(5-

0)1

1)1

2)1

3)!

4)1

(5 - 5)1

1 х(0,2)<>

(0,8)5 = 0,3277

5 х(0,2)'

(0,8)* =

6.4096

10 х(0,У

(О.ЗЯ = 0,2048

10 х(0.2)3

(0,8)2 = 0,0512

5 х(0,2)<

(0,8)' = 0,0064

1 х(0.2)5

(0,8)» = 0,0003

Всего:

1,0000

Дискретное вероятностное распределение Р(г) для всех г можно проиллюстри-

ровать графиком:

Вароятмость i,

0.5

0.4

•

0.3

0.2

0.1

-• '

Число поломок станков

в венк

Рнс. 2.4. Вероятностное распределение поломок

одного из пяти станков в течение дня

Ч. 1.

Принятие решений

условиях

недостатка

информации

2.3.3. Математическое ожидание и стандартное отклонение для

биномиального распределения

Для любой дискретной случайной величины математическое ожидание составляет:

E(r)-j;rP(r),

Может быть показано,

что для

случайной величины

биномиальным распределе-

нием вероятностей:

Е(г)-Х'Р«

пр-

где

—

число опытов;

—

вероятность успеха

каждом

из них;

(г) —

биномиальная вероятность.

Аналогично стандартное отклонение

для

дискретной случайной величины равно:

o-V2;r2p(r)-(XrP(r)7.

Для случайной величины

биномиальным распределением вероятностей:

- ^/Х

г^

(г)

- (^ г Р {t)f -

- р) =

ViTTq

•

Следовательно, диспертия равна

от = Vn р q , где q

— вероятность "неудачи"

в любом

из

опытов.

Эти характеристики биномиального распределения расчитаны

примере

2.S.

О Пример

2.5. По

данньш примера

2.4

найдем математическое ожидание сло-

мавшихся

за

день станков

стандартное отклонение.

Для

расчетов используем

сначала общую формулу

для Е(г) и о, а

потом формулу

для

биномиального

распределения.

Таблица

2.7.

Вероятность поломки

станков

•

день

Число сломавшихся

за день станков

Всего

Вероятность

поломки

Р(г)

0,4096

0,2048

0,0512

0,0064

0,0003

1,0000

тР(т)

0,4096

0,1536

0,0256

0,0015

0,9999

г^Р(г)

0,4096

0,8192

0,4608

0,1024

0,0075

1,7995

Примечание. Значения вероятностей округлены

до

четырех знаков после запятой,

что

приводит

небольшим Погрешностям,

именно: итоговые значения должны быть равны

1,0000 и 1,8000

соотвегственно.

Гл.

Вероятностные распределения

По общей формуле ожидаемое количество поломок в день:

E(r) = X'PW' E(r)-1.0,

по формуле биномиального распределения:

Е(г)-=пр

5х0,2= 1,0 ,

т.е.

ожидаемое количество поломок

—

один станок в день. Стандартное отклонение

по общей формуле:

a = V£r2p(r)-(X;rP(r))2 ,

отсюда

о = Vl.8- 1,0^

0.8944

(до четырех знаков после запятой).

По формуле биномиального распределения:

о = Vnpq -

V5 X

0,2 х 0,8 = 0.8944

(до четырех знаков после запятой),

дисперсия:

npq

5x 0,2

0,8

0,8 .

Иногда нужно знать долю "успехов" в общем количестве опытов. Исходя из

формулы математического ожидания, получим:

Е (доля " успехов" в п опытах)

—^ = р .

Формула стандартного отклонения доли "успехов" имеет следующий вид:

о (доля "успехов")

—^-^

л/Е-^ .

•' п п

Отсюда в примере 2.5, предполагаемая доля поломок станков в день:

^-i=«.^=-

а стандартное отклонение:

г=>Щ|^

0,179

(до трех знаков после запятой).

so Ч. 1. Принятие решений в условиях недостатка информации

Дисперсия доли поломок в день:

„2„М|М.о.032.

О Пример 2.6. Компания производит пружины, 10% из которых оказываются

бракованными. Сто пружин отобраны для контроля качества. Требуется найти

ожидаемое количество бракованных пружин и стандартное отклонение бракован-

ных в отобранных образцах, а также вероятность того, что в выборке по меньшей

мере 15 бракованных пружин.

Решение.

Используем биномиальное распределение, так как:

Имеются 100 идентичных опытов.

Опыты независимы, так как пружины отбираются наугад.

Для каждого опыта возможны два исхода: пружина может бьггь с

дефектом и без оного.

Вероятность, что любая из пружин имеет дефект, равна 0,1. Поскольку

выборка делается из массовой партии, доля бракованных пружин сильно

измениться не может.

Ожидаемое количество пружин с дефектом:

Е (г) = пр = 100

0,1= 10 пружин в выборке.

Стандартное отклонение брака: а = Vnpq :

о =

VlOO X

0,1

0,9 = 3 пружины в выборке.

Вероятность того, что имеется г бракованных образцов в выборке:

Р (г бракованных образцов из 100 едениц) = ""С^ (0,1/

(0,9)"*°

;

г =

О,

1, 2, ..., 100.

Р(г i 15) = Р(15) +

Р{16)

+ ... + Р(100) =

- Р(0) + Р(1) + ... + Р(14) .

Расчеты в данном случае займут много времени и места, поэтому методы

приблизительного вычисления вероятности будут рассмотрены в § 2.5 и 2.8.

2.4. РАСПРЕДЕЛЕНИЕ ПУАССОНА

2.4.1.

Что такое распределение Пуассона

Например, регистрируется количество дорожных происшествий за неделю на опреде-

ленном участке дороги. Это число представляет собой случайную величину, которая

может принимать значения: О, 1,2, 3, ... (верхнего предела нет). Число дорожных

происшествий может быть каким угодно большим. Если рассмотреть какой-либо

короткий временной промежуток в течение недели, скажем минуту, то происшествие

либо произойдет на его протяжении, либо

нет.

Вероятность дорожного происшествия

в течение отдельно взятой минуты очень мала, и примерно такая же она для всех минут.

Га.

2. Вероятностные распределения 51

Распределение вероятностей числа происшествий описывается формулой:

Р(г происшествий

неяелю) = j— , г =

О,

1, 2, 3, ...,

где m — среднее количество происшествий за неделю на определенном

участке дороги;

е — константа, равная 2,718...

Характерные особенности данных, для которых наилучшим образом подходит

распределение Пуассона, следующие:

Каждый малый интервал времени может рассматриваты:я как опыт,

результатом которого является одно из двух: либо прюисшествие

("успех"), либо его отсутствие ("неудача"). Интервалы столь малы, что

может быть только один "успех" в одном интервале, вероятность которого

мала и неизменна.

Число "успехов" в одном большом интервале не зависит от их числа в

другом, т.е. "успехи" беспорядочно разбросаны по временным промежуткам.

Среднее число "успехов" постоянно на протяжении всего времени.

Распределение вероятностей Пуассона может быть использовано не только при

работе со случайными величинами на временных интервалах, но и при учете

дефектов дорожного покрытия на километр пути или опечаток на страницу текста.

Общая формула распределения верюятностей Пуассона:

„г -т

• Р (г "успехов" на заданном интервале) = —j— , г = О, 1, 2, 3, ...,

где m — среднее число "успехов" на единицу.

В таблицах распределения вероятностей Пуассона значения Р(г) табулирова-

ны для определенных значений ш и г.

О Пример 2.7. В среднем на телефонной станции заказывают три телефонных

разговора в течение пяти минут. Какова вероятность, что будет заказано О, 1,2, 3,

4 или больше четырех разговорюв в течение пяти минут?

Решение.

Применим распределение вероятностей Пуассона, так как:

Существует неограниченное количество опытов, т.е. маленьких отрезков

времени, когда может появиться заказ на телефонный разговор, вероят-

ность чего мала и постоянна.

Считается, что спрос на телефонные разговоры беспорядочно распределен

во времени.

Считается, что среднее число телефонных разговоров в любом 5-минут-

ном отрезке времени одинаково.

В этом примере среднее число заказов равно 3 за 5 минут. Отсюда, распреде-

ление Пуассона:

Р (г заказов за 5 минут) = —;— , г =

О,

1, 2, 3, 4, ...,

52 Ч. 1. Принятие решений в условиях

недостатка информации

3° е~^

Р (О заказов за 5 минут) = Р (0) =

j х 0,0498

0,0498 ;

З'

е~^ 3

Р (1 заказа за 5 минут) = Р (1)

—тр

у х Р (0)

3 х 0,0498 = 0,1494 ;

Р (2 заказа за 5 минут) = Р (2)

^-^

| х Р (1)

| х 0,1494 = 0,2240 ;

Р (3 заказа за 5 минут) = Р (3)

| х Р (2)

| х 0,2240 = 0,2240 ;

Р (4 заказа за 5 минут) = Р (4)

^-^

•=

I " Р (3)

| х 0,2240 » 0,1680 ;

41 4 4

Р (более 4 заказов за 5 минут) = {Р(5) + Р(6) + Р(7) + Р(8) + ...} =

- {Р(0) + Р(1) + Р(2) + Р(3) + Р(4)}

{0.0498

0,1494

0,2240

0,1680}

0,8152

0,1848.

При распределении вероятностей Пуассона, зная среднее число "успехов" на

5-минутном промежутке (например т, как в примере 2.7 ), для того чтобы узнать

г среднее число "успехов" за один час, нужно просто умножить m на 12. В

примере 2.7 среднее число заказов в час составит: 3 х 12 = 36. Аналогично, если

требуется определить среднее-число заказов в минуту: m = 3/5 = 0,6.

О Пример 2.8. В среднем за пять дней рабочей недели на автоматической линии

происходят 3,4 неполадок. Какова вероятность двух неполадок в каждый день работы?

Решение.

Можно применить распределение Пуассона:

Существует неограниченное количество опытов, т.е. малых промеж)ггков

времени, в течение каждого из них может произойти или не произойти

неполадка на автоматической линии. Вероятность этого для каждого

промежутка времени мала и постоянна.

Предполагается, что неполадки беспорядочно расположены во времени.

Предполагается, что срюднее число неполадок в течение любых пяти дней

постоянно.

Среднее число неполадок равно 3, 4 за пять дней. Отсюда число неполадок в день:

3,4

, --0,68

Следовательно,

68'

е"*'^

Р(г неполадок в день) =

—

; , г =

О,

1, 2, 3, ...