Дыхта В.А. Динамические системы в экономике. Введение в анализ одномерных моделей
Подождите немного. Документ загружается.


λ ∈ (1; 2] x ∈ (x
∗
;
1
2
)
lim
p→∞
f
p
λ
(x) = x
∗
.
λ ∈ (3, 1 +
√
6).
x
t+1
= x
2
t
+c
x
∗
1
, x
∗
2
c x
∗
1
x
∗
2
c
0
c > c
0
Q
λ
(x) = 1 − λx
2
λ ∈ (0, 2]
x
t+1
= x
t
+
1
π
sin(2πx
t
)
x
t+1
= 0, 5 sin(πx
t
)
x
t+1
= 2x
t
exp(−x
t
)
x
t+1
=
½
3, 2x
t
, 0 ≤ x
t
≤ 1,
0, 5x
t
, x
t
> 1.
Q
Dt
= 2 − P
t
,
Q
St
= P
1
2
t−1

x
t+1
= 3x
t
− 3x
2
t
− υ
t
, t = 0, 1, 2, . . . ,
υ
t
υ
t
≡
7
48
υ
t
≡
1
3
υ
t
= cx
t
,
c > 0
N
t+1
− N
t
N
t
= r −
b
w
t
, t = 0, 1, 2, . . . ,
N
t
t w
t
r, b > 0
r
w
t
= Y
t
/N
t
Y
t
= N
α
t
, 0 < α < 1
N
t+1
= N
t
(1 + r − bN
1−α
t
).
f(N)

N =
·
1 + r
b(2 − α)
¸
1
1−α
.
N
∗
= r/b
N
∗
r(1 − α) < 2.
r
α
r

F (t, y, y
0
)
0
= 0, (3.1)
t y = y(t)
y
0
= y
0
(t) = dy/dt F
t y y
0
t
y + t
2
− 1 = 0, y(t + 3) − y(t + 1) = 0, y
µ
t
t
2
+ 1
¶
− t
2
= 0

y y(t) = 1 − t
2
t
y = ϕ(t)
y
0
= ϕ
0
(t)
F (t, ϕ(t), ϕ
0
(t)) = 0. (3.2)
y = ϕ(t) I = (a, b)
a = −∞ b = +∞
ϕ(t) I
t ∈ I
I ϕ(t)
ϕ(t)
I
y = ϕ(t) =
sin t
t
ty
0
+ y = cos t
I
1
= (−∞, 0) I
2
= (0, +∞)
ϕ(t)
y
0
= ϕ
0
(t) =
t cos t − sin t
t
2
(t 6= 0).
y y
0
t
t cos t − sin t
t
2
+
sin t
t
= cos t (t 6= 0),
F
t y y
0
(t, ϕ(t), ϕ
0
(t)) ∈ D D
F

2
y y
0
ϕ ϕ
0
ϕ(t)
y(t)
y
0
− y
2
= 0, y
0
= y
2
, (3.3)
y(t) =
1
C − t
= (C − t)
−1
, (3.4)
C
t 6=
C I
1
= (−∞, C) I
2
= (C, +∞)
y
0
(t) =
1
(C − t)
2
= y
2
(t).
y(t)
C
I
1
I
2
I
1
I
2
t = C C
y(t) ≡ 0
C
t → C
C
y = y
0
t = t
0
, y(t
0
) = y
0
.
t
0
y
0

y
0
= y
2
, y(0) = y
0
(t
0
= 0, y
0
6= 0)
y(t) =
y
0
1 − y
0
t
.
y
0
> 0 t < 1/y
0
y(t) → +∞ t → 1/y
0
y
Ax = b
y = Φ(t, C)
C
Φ
C
y
0
− ay = 0, y
0
= ay (3.5)
y = Φ(t, C) = Ce
at
; (3.6)
(t
0
, y
0
)
y = ϕ(t) = y
0
e
a(t−t
0
)
(3.7)
C = y
0
e
−t
0

I
1
I
2
y ≡ y
∗
= 0
(y
0
)
2
− 4y = 0 (3.8)
y = Φ(t, C) = (t + C)
2
y ≡ y
∗
= 0
C
(t, y)
t y = ϕ(t)
(t
0
, y
0
) (t, y)
F
(t, y)
C
(t, y)
(t
0
, y
0
)
y > 0
(−∞, C) (C, +∞)
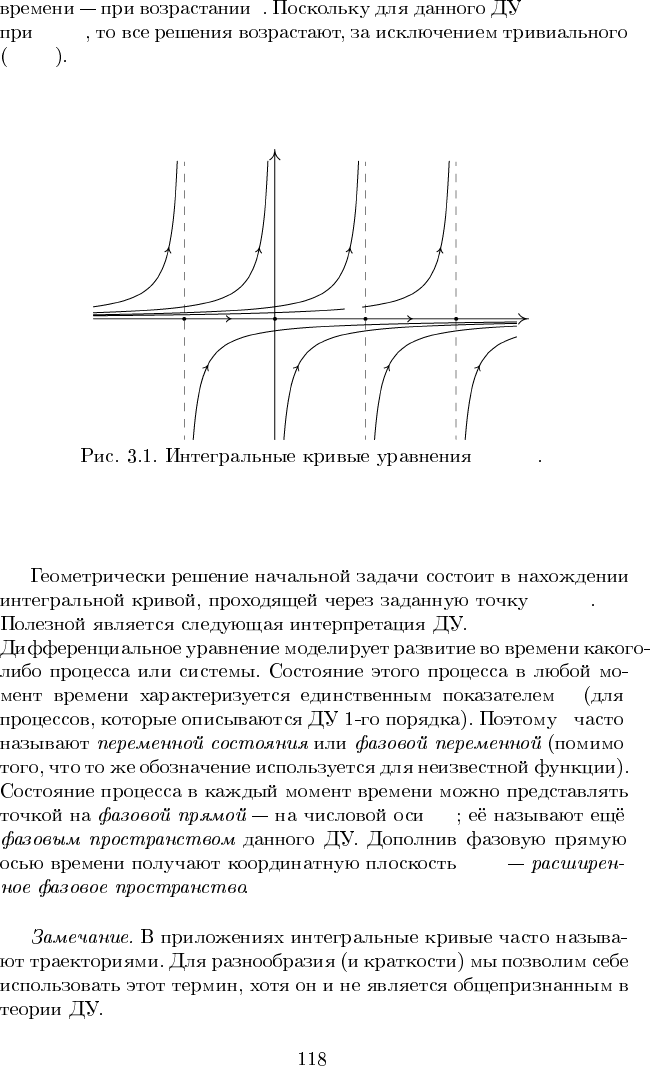
t y
0
= y
2
> 0
y 6= 0
y ≡ 0
t
y
C
y
0
= y
2
(t
0
, y
0
)
y
y
Oy
(t, y)

y
0
y
0
= f(t, y), (3.9)
f(t, y)
y
t+1
= y
t
+ f(t, y).
f(t, y)
(t, y)
(t, y)
k f(t, y)
f(t, y)
t
y
D
D
y
0
t y
y
0
t y
