Dunajski M. Solitons, Instantons, and Twistors
Подождите немного. Документ загружается.


186 8: Symmetry reductions and the integrable chiral model
we shall fill in the details in [179] and describe this compactification and its
corresponding compactified space-time
M = RP
3
.
Let us first notice that the non-compact mini-twistor space Z = TCP
1
is bi-
holomorphic to the quadratic cone in CP
3
minus the vertex. Indeed, let [Z
0
:
Z
1
: Z
2
: Z
3
] be homogeneous coordinates in CP
3
, and let T be a cone
(Z
1
)
2
+(Z
2
)
2
+(Z
3
)
2
=0.
The map from the mini-twistor space TCP
1
to the cone is given by
(λ, µ) → [−2µ, 1 − λ
2
, −2λ, −i(1 + λ
2
)] in the patch λ = 0 and
(
˜
λ, ˜µ) → [2 ˜µ,
˜
λ
2
− 1, 2
˜
λ, i(1 +
˜
λ
2
)] in the patch
˜
λ =0,
where on the overlap
˜
λ =
1
λ
and ˜µ =
µ
λ
2
.
In the patch of CP
3
where Z
0
= 0 the cone T is
(z
1
)
2
+(z
2
)
2
+(z
3
)
2
=0, (8.2.81)
where z
i
= Z
i
/Z
0
are inhomogeneous coordinates on CP
3
. Now consider a
plane P ⊂ CP
3
which omits the vertex [1 : 0:0:0].Planes in CP
3
are of the
form P
α
Z
α
= 0, so we need P
0
= 0, and thus the plane is
1+z
1
x
1
+ z
2
x
2
+ z
3
x
3
=0, (8.2.82)
where x
i
= P
i
/P
0
. Those planes correspond to points in complexified
Minkowski space M
C
= C
3
, that is,
P ↔ p =(x
1
, x
2
, x
3
) ∈ M
C
.
The real planes (with P
α
real) are parameterized by points in the real
Minkowski space M = R
2,1
.
The conic sections in T corresponding to points in M
C
are given by the locus
of (8.2.81) and (8.2.82). Two planes P, P
intersect in a line, which intersects
a cone in two points Z, Z
and all conics (8.2.82) through Z, Z
correspond to
geodesics in M
C
joining p and p
. In the special case if the planes touch on the
cone the geodesic is null (Figure 8.2). Now consider a compactification of M
C
by including the planes through the vertex, that is, allowing P
0
= 0. The space
M
C
of such real planes has homogeneous coordinates
[P
0
: P
1
: P
2
: P
3
]
so
M
C
= CP
3
. The ‘added planes’ are of the form 0 + P
1
Z
1
+ P
2
Z
2
+ P
3
Z
3
=0,
and are parameterized by [P
1
: P
2
: P
3
] which is
ˆ
J = CP
2
. Therefore
M
C
= C
3
∪ CP
2
.
8.2 Integrable chiral model 187
Geodesic
Null geodesic
T
Z
Z
Z
'
Z
P
P
'
Z
'
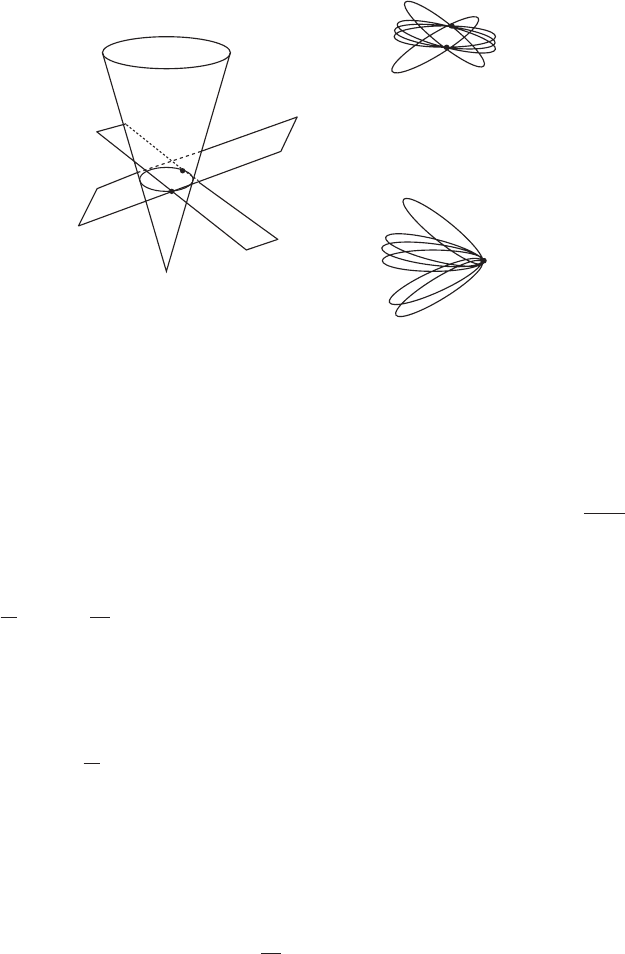
Figure 8.2 A geodesic joining two points in the complexified Minkowski space corresponds to all conic
sections intersecting at two points. The null geodesics arise as a limiting case
These additional planes intersect the cone in the generator lines which pass
through the vertex. To construct the compactified mini-twistor space
¯
T blow
up the vertex and replace it by a line L
∞
= CP
1
(Figure 8.3). The resulting
compact complex two-fold is called the Hirzebruch surface and denoted
O(2)
to stress that each fibre of O(2) → CP
1
has been compactified. The lines in
¯
T
corresponding to points on
ˆ
J intersect L
∞
. From our discussion it is clear that
there is a one-to-one correspondence between the following geometric objects
in T,
O(2), and M:
1. A generator λ of a cone T ⊂ CP
3
2. A pencil of planes through that generator
3. One-parameter family of null planes in the space time with the same normal
π
A
π
B
, where λ = π
0
/π
1
4. A fibre λ of O(2) → CP
1
After the blow-up all the CP
1
–worth of generators become disjoint, and cor-
respond to points on L
∞
, therefore a point on L
∞
corresponds, via (2), to a
line
l
λ
∈
ˆ
J = CP
2
⊂ CP
3
(we recall that
ˆ
J is the infinity of M
C
corresponding to the vertex J of the
cone). This is however not a one-to-one correspondence. The planes through
the vertex are not disjoint after the blow-up.
There is a unique plane through any two generators λ
1
and λ
2
of the cone.
This plane corresponds to the intersection point L
12
of two lines l
λ
1
and l
λ
2

188 8: Symmetry reductions and the integrable chiral model
L
L
Ó
L
Ó
Blow up
CP
1
T
T = O(2)
L
Î
L
Î
Figure 8.3 Blow-up of the vertex of the cone. Planes thorough the vertex correspond to points at
infinity in
M
in
ˆ
J . Any point in
ˆ
J corresponds to two or one fibres in that way, as any
generator also corresponds to a point, because it determines a unique tangent
plane to a cone.
Any finite point p ∈
M
C
= CP
3
∗
corresponds to a section L
p
of O(2) which
intersects the line L
12
at two points (respectively, one point for a point in
ˆ
J ). The set of all sections of
O(2) through these two points is a geodesic
(respectively, a null geodesic) joining p to L
12
. This geodesic is compactified to
a projective line in the space-time by inclusion of L
12
.
All these structures are compatible with the real structure corresponding to
real planes in CP
3
. Thus the compactified Minkowski space is
M = R
3
∪ RP
2
.
8.2.5.4 Initial value problem
Let ! be a non-null plane in the complexified Minkowski space C
3
.Toany
such plane we can associate an involution σ
!
: Z → Z defined as follows.
Given a null plane Z in C
3
we define σ
!
(Z) to be a null plane such that the
pair of planes (Z,σ
!
(Z)) intersect ! in the same line. Take ! to be a space-
like plane t = 0 with a normal vector t = t
AB
∂
AB
. Then the involution σ acts on
homogeneous coordinates on the twistor space by
σ (ω, π
A
)=(−ω, t
A
B
π
B
),

8.2 Integrable chiral model 189
or, in the inhomogeneous form,
σ (µ, λ)=
−
µ
λ
2
, −
1
λ
.
The fixed points of this involution have λ = ±i. The σ -invariant sections of
TCP
1
→ CP
1
correspond to points in the t = 0 plane in Minkowski space.
The involution σ commutes with the real structure
τ :(ω, π
A
)=(ω, π
A
).
These two involutions fix a real space-like plane in R
2,1
.
Now consider the compactified picture. The space-like plane t = 0 intersects
ˆ
J in CP
1
∞
. Any point on L
∞
corresponds to a point on CP
1
∞
.Toseeit
consider the generator λ of the cone, and draw the unique plane through λ
and (the generator corresponding to) −1/λ. These two generators are swapped
by the involution τ , and so the point corresponding to this plane belongs to
CP
1
∞
. However this is not a bijection, as any point in CP
1
∞
corresponds to
two generators, and so two points of L
∞
(the special case is λ = ±i).
Exercises
1. Show that the generators of the conformal group are given by (8.1.1).
2. Use the zero-curvature representation (3.3.12) to show that the NLS equa-
tion is a symmetry reduction of ASDYM.
[Hint: Proceed by analogy with the calculation leading to KdV Lax pair
(8.1.3).]
3. Find the energy functional corresponding to the Lagrangian (8.2.10) and
show that the energy density vanishes on solutions to (8.2.8).
4. Use the Bäcklund relations (8.2.39) to obtain the two-soliton solution
(8.2.25) starting from the one-soliton (8.2.23).
5. Verify that the WZW action (8.2.41) gives rise to the integrable chiral
equation (8.2.13).
6. Show that a conformal Killing vector K = K
AA
∂
AA
on the complexified
four-dimensional Minkowski space maps α-planes to α-planes and gives
rise to a holomorphic vector field on the corresponding twistor space given
by
K = K
AA
π
A
∂
∂ω
A
+ φ
A
B
π
B
∂
∂π
A
for some φ
A
B
which should be determined.
190 8: Symmetry reductions and the integrable chiral model
Describe the infinitesimal conformal group action on the space of SD two-
forms in terms of φ
A
B
.
7. Assume that K in the previous question is a non-null translation so that
φ
A
B
= 0. Obtain the mini-twistor space TCP
1
as a quotient of the twistor
space PT = CP
3
− CP
1
by K. Conversely, show that PT is a holomorphic
bundle over TCP
1
and determine the transition functions for this bundle.

9
Gravitational instantons
Gravitational instantons are solutions to the four-dimensional Einstein equa-
tions in Riemannian signature which give complete metrics and asymptotically
‘look-like’ flat space, in a sense to be made precise in the remainder of this
chapter. Gravitational instantons cannot usually be analytically continued to
Lorentzian signature. They are nevertheless physically relevant as they can
allow a semi-classical description of the as-yet-unknown theory of quantum
gravity. Our discussion in this chapter assumes familiarity with basic general
relativity, but we shall summarize the standard definitions in Section 9.2.
9.1 Examples of gravitational instantons
r
Example. Euclidean Schwarzchild solution. Our first example will be an
analytic continuation of a well-known solution describing a static black hole.
Replacing t by iτ in the Schwarzchild metric gives the following Riemannian
metric:
g =
1 −
2m
r
−1
dr
2
+
1 −
2m
r
dτ
2
+ r
2
(dθ
2
+sin
2
θdφ
2
). (9.1.1)
The metric g is an analytic continuation of a Ricci-flat metric, therefore g
itself is Ricci-flat and there is no need to verify the Einstein equations.
The Schwarzchild metric in the Lorentzian signature is singular at r =0,
but in the Riemannian setting this singularity can be removed by considering
the range 2m ≤ r < ∞. The apparent singularity at r =2m can also be
avoided at the price of allowing τ to be periodic. To see this define
ρ =4m
1 −
2m
r
.

192 9: Gravitational instantons
Expanding the metric near ρ = 0, which corresponds to r =2m, gives
dr ∼ (ρ/4m)dρ and
g ∼ dρ
2
+
ρ
2
16m
2
dτ
2
+4m
2
(dθ
2
+sin
2
θdφ
2
).
If τ is taken to be periodic with a period of 8πm then the term dρ
2
+
ρ
2
16m
2
dτ
2
describes the flat metric on R
2
and the four-dimensional metric g is regular.
For the next two examples we need to introduce left-invariant one-forms σ
i
, i =
1, 2, 3, on the group manifold SU(2) such that
dσ
1
+ σ
2
∧ σ
3
=0, dσ
2
+ σ
3
∧ σ
1
=0, and dσ
3
+ σ
1
∧ σ
2
=0.
(9.1.2)
These one-forms can be represented in terms of Euler angles by
σ
1
+ iσ
2
= e
−iψ
(dθ + i sin θdφ) and σ
3
= dψ + cos θ dφ,
where to cover SU(2) = S
3
we require the ranges
0 ≤ θ ≤ π, 0 ≤ φ ≤ 2π, and 0 ≤ ψ ≤ 4π.
In terms of the left-invariant one-forms the flat metric on R
4
is given by
g
flat
= dρ
2
+
1
4
ρ
2
*
σ
2
1
+ σ
2
2
+ σ
2
3
+
,
where ρ ≥ 0.
The following two examples do not arise as analytic continuations of
Lorentzian solutions. Their Riemann tensor is ASD which makes them anal-
ogous to the ASD instantons in YM theory studied in Section 6.4. We shall
postpone the discussion of the ASD condition to the next section and here only
give the expressions for the metrics. We shall demonstrate that the expressions
give rise to regular metrics but leave the verification of the Ricci-flat condition
to Section 9.4 where a convenient formalism is developed.
r
Example. Eguchi–Hanson metric. The Eguchi–Hanson metric [60, 61] is
given by
g =
1 −
a
4
r
4
−1
dr
2
+
1
4
r
2
1 −
a
4
r
4
σ
2
3
+
1
4
r
2
*
σ
2
1
+ σ
2
2
+
. (9.1.3)
The apparent singularity at r = a is removed by allowing
r > a, 0 ≤ ψ ≤ 2π, 0 ≤ φ ≤ 2π, and 0 ≤ θ ≤ π.

9.1 Examples of gravitational instantons 193
To see that the metric is complete set ρ
2
= r
2
%
1 − (a/r)
4
&
. Expanding the
metric near r = a and fixing (θ,φ) gives
g ∼
1
4
*
dρ
2
+ ρ
2
dψ
2
+
.
In the standard spherical polar coordinates ψ has a period 4π on SU(2). In
our case the period of ψ is 2π to achieve regularity. Therefore the surfaces
of constant r are real projective planes defined by identifying the antipodal
points on the sphere, RP
3
= S
3
/Z
2
. At large values of r the metric looks like
R
4
/Z
2
rather than Euclidean space. The Eguchi–Hanson metric is an example
of the asymptotically locally euclidean (ALE) manifold.
The Eguchi–Hanson example motivates the following definition:
Definition 9.1.1 A complete regular four-dimensional Riemannian manifold
(M, g) which solves the Einstein equations (possibly with cosmological con-
stant) is called ALE if it approaches R
4
/ at infinity, where is a discrete
subgroup of SO(4).
If contains only the identity then asymptotically g is Euclidean and Ricci-flat.
The positive action theorem [183] implies that any such g is a flat metric on R
4
.
The Eguchi–Hanson metric corresponds to generated by a single reflection.
The following example also has ASD Riemann tensor, but its asymptotic
behaviour is rather different from that of the Eguchi–Hanson metric.
r
Example. Taub-NUT gravitational instanton. Consider the metric [77]
g =
1
4
r + m
r − m
dr
2
+ m
2
r − m
r + m
σ
2
3
+
1
4
(r
2
− m
2
)
*
σ
2
1
+ σ
2
2
+
. (9.1.4)
At r = m the three-sphere of constant r collapses to a point – an example of a
NUT singularity (see below). The change of variables r = m + ρ
2
/(2m) gives
near r = m
g ∼ dρ
2
+
ρ
2
4
*
σ
2
1
+ σ
2
2
+ σ
2
3
+
,
where we set r + m ∼ 2m in all numerators. Thus the metric extends
smoothly over this point, and therefore is defined on the whole of R
4
. This
metric is not ALE as the coefficient of σ
2
3
approaches a constant as r →∞
while the coefficient of (σ
2
1
+ σ
2
2
) grows like r
2
. Thus the circle generated
by σ
3
separates from the three-sphere at large distances. The infinity has
a topology of the S
1
bundle over S
2
. Examining the transition functions
shows that this is in fact the one-monopole bundle considered in Section
6.2.1. This kind of behaviour is referred to as asymptotic local flatness. It
implies flatness in the three-dimensional sense. The fourth (imaginary time)
dimension is periodic.

194 9: Gravitational instantons
Definition 9.1.2 A complete regular four-dimensional Riemannian manifold
(M, g) which solves the Einstein equations (possibly with cosmological con-
stant) is called ALF (asymptotically locally flat) if it approaches S
1
bundle
over S
2
at infinity.
The case when the asymptotic bundle is globally S
1
× S
2
corresponds to
asymptotically flat metrics. The Euclidean Schwarzchild solution (9.1.1) is one
example. The ALE and ALF manifolds belong to the class of gravitational
instantons because their curvature is concentrated in a finite region of a
space-time.
We shall end this section by discussing the removable singularities of the
metrics (9.1.3) and (9.1.4) in a more general context. Consider a general metric
of the form
g = dr
2
+ a
1
(r)σ
2
1
+ a
2
(r)σ
2
2
+ a
3
(r)σ
2
3
.
This metric is regular if the functions a
i
(r) are regular and non-vanishing. It
can however be regular even if some of the functions vanish, as the apparent
singularity may result from choosing a singular coordinate system. Following
Gibbons and Hawking [72] we consider two types of removable singularities
at r =0.
r
The metric has a removable NUT singularity if
a
1
(r)
2
= a
2
(r)
2
= a
3
(r)
2
=
r
2
4
+ O(r
3
)
near r = 0. This singularity may be removed by using the Cartesian coordi-
nate system near the origin. The singularity r = m in the Taub-NUT metric
(9.1.4) is an example of a NUT singularity.
r
The metric has a bolt singularity if
a
1
(r)
2
= a
2
(r)
2
= const and a
3
(r)
2
= n
2
r
2
, where n ∈ Z
up to the higher order terms in r near r = 0. Let us set the constant to one
without the loss of generality. Thus near the bolt singularity the metric is of
the form
g ∼ dr
2
+
n
2
r
2
4
(dψ + cos θ dφ)
2
+
1
4
(dθ
2
+sin
2
θdφ
2
)
up to the higher order terms. This can be made regular if ψ is a periodic
coordinate with the adjusted range
0 ≤ ψ ≤
4π
n
as then the singularity for fixed values of (θ,φ) just arises from using
the plane polar coordinates (r,ψ) and can be removed by using Cartesian

9.2 Anti-self-duality in Riemannian geometry 195
coordinates on R
2
. Thus at the bolt singularity r = 0 the three-dimensional
orbits of the SU(2) action collapse to a two-sphere S
2
with constant radius.
The r = a singularity in the Eguchi–Hanson metric (9.1.3) is an example of a
bolt.
9.2 Anti-self-duality in Riemannian geometry
Let (M, g)beann-dimensional Riemannian manifold. Thus there exists a non-
degenerate symmetric tensor g
µν
= g
µν
(x)onM giving rise to a line element
g = g
µν
dx
µ
⊗ dx
ν
,µ,ν=1,...,n.
A linear connection ∇ on M is a map sending a pair of vector fields (X, Y)on
M to a vector field ∇
X
Y such that for any vector fields X, Y, Z and any function
f on M we have
r
∇
X
( fY)= f ∇
X
Y + X( f )Y
r
∇
X
( f )=X( f )
r
∇
X
(Y + Z)=∇
X
(Y)+∇
X
(Z)
r
∇
X+ fY
Z = ∇
X
Z + f ∇
Y
Z
If ∂
µ
= ∂/∂x
µ
is a coordinate basis for vector fields we can define the Christoffel
symbols by
∇
∂
µ
∂
ν
=
λ
νµ
∂
λ
.
Moreover we define ∇
µ
:= ∇
∂
µ
. The Levi-Civita connection ∇ is the unique
connection on TM that is torsion-free, that is,
[∇
µ
, ∇
ν
] f =0
for any function f on M, and preserves the metric, that is, ∇
µ
g
νλ
= 0. From
now on we shall assume that ∇ is the Levi-Civita connection.
Expanding the expressions ∇
X
V where X = X
µ
∂
µ
and V = V
µ
∂
µ
using the
properties of ∇ we find that the covariant derivative of a vector V
µ
and a form
V
µ
are given by
∇
µ
V
ν
= ∂
µ
V
ν
+
ν
µλ
V
λ
and ∇
µ
V
ν
= ∂
µ
V
ν
−
λ
µν
V
λ
,
respectively, where the Christoffel symbols
λ
µν
of the Levi-Civita connection
are uniquely determined by the metric
γ
µν
=
1
2
g
γδ
∂g
µδ
∂x
ν
+
∂g
νδ
∂x
µ
−
∂g
µν
∂x
δ
. (9.2.5)
