Dunajski M. Solitons, Instantons, and Twistors
Подождите немного. Документ загружается.


156 8: Symmetry reductions and the integrable chiral model
There exists a different positive functional associated to (8.2.8). To see it,
note that the equations (8.2.8) arise as the integrability conditions for an
overdetermined system of linear Lax equations:
L
0
= 0 and L
1
=0, where L
0
= D
y
+ D
t
− λ(D
x
+ ) and
L
1
= D
x
− − λ(D
t
− D
y
), (8.2.11)
which is the reduction of the ASDYM Lax pair (7.1.6). The extended solution
is a GL(n, C)-valued function of x
µ
and a complex parameter λ ∈ CP
1
,
which satisfies the unitary reality condition
(x
µ
, λ)
∗
(x
µ
,λ)=1. (8.2.12)
The matrix is also subject to gauge transformation −→ g. The inte-
grability conditions for (8.2.11) imply the existence of a gauge A
t
= A
y
and
A
x
= −, and a matrix J : R
3
−→ U(n) such that
A
t
= A
y
=
1
2
J
−1
(J
t
+ J
y
) and A
x
= − =
1
2
J
−1
J
x
,
where J
µ
= ∂
µ
J . With this gauge choice the equations (8.2.8) become
(J
−1
J
t
)
t
− (J
−1
J
x
)
x
− (J
−1
J
y
)
y
− [J
−1
J
t
, J
−1
J
y
]=0. (8.2.13)
A positive-definite conserved energy functional can now be introduced by
E =
R
2
Edxdy, (8.2.14)
where the energy density is given by
E = −
1
2
Tr
%
(J
−1
J
t
)
2
+(J
−1
J
x
)
2
+(J
−1
J
y
)
2
&
. (8.2.15)
This came at the price of losing the full Lorentz invariance since the commuta-
tor term fixes a space-like direction. If we rewrite (8.2.13) as
(η
µν
+ V
α
ε
αµν
)∂
µ
(J
−1
∂
ν
J )=0
then the fixed direction is given by
1
a space-like vector V = ∂/∂x. This breaks
the symmetry to SO(1, 1). In general the finiteness of E is ensured by imposing
the boundary condition (valid for all t)
J = J
0
+ J
1
(ϕ)r
−1
+ O(r
−2
)asr −→ ∞, x + iy = re
iϕ
(8.2.16)
1
Manakov and Zakharov [110] studied a closely related system of equations where the unit
vector V was taken to be time-like. The resulting equations do not appear to have a positive-
definite energy functional, and no static solutions can exist globally on R
2
.

8.2 Integrable chiral model 157
where J
0
is a constant matrix, and so for a fixed value of t the matrix J extends
to a map from S
2
(the conformal compactification of R
2
)toU(n).
The equation (8.2.13) is known as the Ward model or the integrable chiral
model [173, 176, 177]. The ordinary chiral model in (2+1) dimensions
η
µν
∂
µ
(J
−1
∂
ν
J )=0
has V = 0. It is fully Lorentz–invariant, but it lacks integrability, and explicit
time-dependent solutions (other than trivial Lorentz boosts of static solutions)
cannot be constructed. In the remainder of this chapter we shall study the
solutions and properties of (8.2.13).
We shall finish this section by presenting another gauge choice leading to
a different potential formulation of (8.2.8). Choose the familiar gauge A
y
=
A
t
, A
x
= −. The vanishing of the term proportional to λ in the compatibility
conditions (8.2.11) implies the existence of K : R
2,1
−→ u(n) such that
A
y
= A
t
=
1
2
K
x
and A
x
= − =
1
2
(K
t
− K
y
),
where K
µ
= ∂
µ
K. The zeroth-order term in the compatibility conditions now
yields
K
tt
− K
xx
− K
yy
+[K
x
, K
t
− K
y
]=0. (8.2.17)
The relation between K ∈ u(n) and J ∈ U(n)is
K
x
= J
−1
(J
t
+ J
y
) and K
t
− K
y
= J
−1
J
x
,
and exhibits a duality between the two formulations: the compatibility condi-
tion K
xt
− K
xy
= K
tx
− K
yx
yields the field equation (8.2.13). The K-equation
(8.2.17) admits a Lagrangian formulation with the Lagrangian density
−Tr
1
2
*
(K
t
)
2
− (K
x
)
2
− (K
y
)
2
+
−
1
3
K[K
x
, K
t
− K
y
]
.
The Lagrangian formulation of (8.2.13) is more complicated – we shall present
it in Section 8.2.2.
8.2.1 Soliton solutions
One method [173] of constructing explicit solutions is based on the associated
linear problem (8.2.11). Let (x
µ
,λ) be the fundamental matrix solution to
the Lax pair (8.2.11) and let u =(t + y)/2,v =(t − y)/2. Then
A
u
− λ(A
x
+ )=(−∂
u
+ λ∂
x
)
−1
and
A
x
− − λ A
v
=(−∂
x
+ λ∂
v
)
−1
, (8.2.18)

158 8: Symmetry reductions and the integrable chiral model
and in the gauge leading to (8.2.13) we have A
v
= A
x
+ = 0. Thus in this
gauge given a solution to the linear system (8.2.11) one can construct a
solution to (8.2.13) by
J (x
µ
)=
−1
(x
µ
,λ = 0) (8.2.19)
and all solutions to (8.2.13) arise from some . This can be an effective method
of finding solutions (also known as the ‘Riemann problem with zeros’), if we
know (x
µ
,λ) in the first place. One class of solutions can be obtained by
assuming that
= 1 +
m
k=1
N
k
(x, y, t)
λ − µ
k
, where µ
k
= const. (8.2.20)
Let us restrict to the case where G = SU(2). The unitarity condition (8.2.12)
implies rank N
k
= 1. Thus (N
k
)
αβ
= n
k
α
m
k
β
. Demanding that the RHS of (8.2.18)
is independent of λ (like the LHS) yields N
k
= N
k
(ω
k
), where
ω
k
= uµ
2
k
+ xµ
k
+ v.
It also follows that
n
k
α
= −
m
l=1
(
−1
)
kl
m
l
α
where the m × m matrix is given by
kl
=
2
α=1
(µ
k
− µ
l
)
−1
m
α
k
m
α
l
.
We can use the homogeneity of the extended solution in m
k
α
to rescale m
k
α
and
set m
k
α
=(1, f
k
(ω
k
)). Finally, dividing by the square root of its determinant
to achieve det = 1 yields
(J
−1
)
αβ
= χ
−1/2
δ
αβ
+
k,l
µ
−1
k
(
−1
)
kl
m
α
l
m
k
β
, where χ =
m
,
k=1
µ
k
µ
k
.
(8.2.21)
The soliton solutions correspond to rational functions f
k
(ω
k
).
r
Example. The solution (8.2.21) with m = 1 and µ
1
= µ = |µ|e
iφ
is given by
J
1
=
1
1+| f |
2
e
iφ
+ e
−iφ
| f |
2
2i sin φ f
2i sin φ
fe
−iφ
+ e
iφ
| f |
2
, (8.2.22)
where f = f (uµ
2
+ xµ + v) is a holomorphic, rational function.

8.2 Integrable chiral model 159
To obtain the static solution put µ = i which gives
J =
i
1+| f |
2
1 −|f |
2
2 f
2
f | f |
2
− 1
, (8.2.23)
where the holomorphic function f is rational in z = x + iy and f (z) −→ 1as
|z|−→∞. All such maps are classified by integer winding numbers N with
values in π
2
(S
2
)=Z. This integer is precisely the degree of f : for a given N,
f is of the form
f (z)=
p(z)
r(z)
=
(z − p
1
) ···(z − p
N
)
(z − r
1
) ···(z −r
N
)
. (8.2.24)
The N static lumps are positioned at ( p
1
,..., p
N
), as the maxima of E
occur at these points. For µ = ±i there is time dependence, and m > 1 corre-
sponds to m solitons moving with different velocities which however do not
scatter.
Allowing to have poles of order higher than one gives solutions which
exhibit soliton scattering. Explicit time-dependent solutions corresponding to
scattering can be obtained by choosing µ
1
= i + ε, µ
2
= i − ε in (8.2.20) with
m = 2 and taking the limit ε → 0. This yields [178]
J
2
=
1 −
2q
1
∗
⊗ q
1
||q
1
||
2
1 −
2q
2
∗
⊗ q
2
||q
2
||
2
, (8.2.25)
where
q
1
=(1, f ), q
2
=(1+| f |
2
)(1, f ) − 2i(tf
+ h)( f , −1), (8.2.26)
and f and h are rational functions of z = x + iy. In [178] 90
◦
scattering is illus-
trated by choosing f = z and h = z
2
. The positions of the solitons correspond
to the maxima of the energy density which in this case is given by
E =
128
3x
2
+3y
2
− 10tx
2
+10ty
2
+ t
2
x
2
+ t
2
y
2
− 4t
2
− 3x
4
− 6x
2
y
2
− 3y
4
+1
*
4t
2
+8tx
2
− 8ty
2
+5x
4
+10x
2
y
2
+5y
4
+1+2x
2
+2y
2
+
2
.
The following series of plots of this energy density demonstrates soliton scat-
tering. Two solitons approach along the x-axis, collide by forming a ring, and
finally move away scattered by 90
◦
along the y-axis.
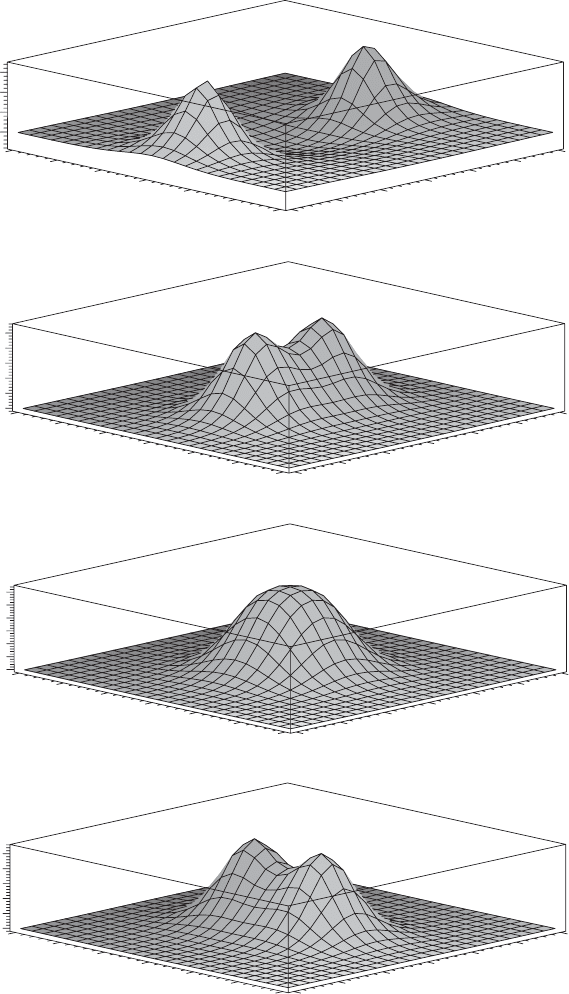
160 8: Symmetry reductions and the integrable chiral model
Two-soliton scattering. Energy density at times t = −1, −0.2, 0, 0.2, and 1.
t = – 1
–1.5
–1
–0.5
0
0.5
1
1.5
x
–1.5
–1
–0.5
0
0.5
1
1.5
y
0
20
40
60
t = – 0.2
–1.5
–1
–0.5
0
0.5
1
1.5
x
–1.5
–1
–0.5
0
0.5
1
1.5
y
0
20
40
60
80
100
t = 0
–1.5
–1
–0.5
0
0.5
1
1.5
x
–1.5
–1
–0.5
0
0.5
1
1.5
y
0
20
40
60
80
100
120
t = 0.2
–1.5
–1
–0.5
0
0.5
1
1.5
x
–1.5
–1
–0.5
0
0.5
1
1.5
y
0
20
40
60
80
100
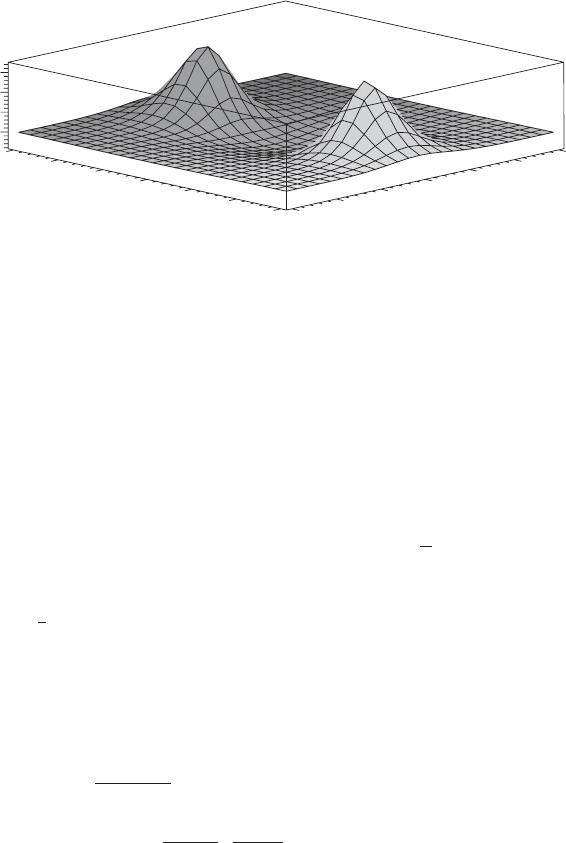
8.2 Integrable chiral model 161
t = 1
–1.5
–1
–0.5
0
0.5
1
1.5
x
–1.5
–1
–0.5
0
0.5
1
1.5
y
0
20
40
60
More complicated examples were considered in [35, 86].
8.2.1.1 ‘Trivial-scattering’ boundary condition
The last example fits into a class of time-dependent solutions which depend
on finite number of parameters. This finiteness of the energy alone does not
pick this finite-dimensional family and one needs stronger boundary conditions
which we shall now describe.
Let us restrict from R
2,1
× CP
1
to the space-like plane t = 0. We shall also
restrict the spectral parameter to lie in the real equator S
1
⊂ CP
1
parameter-
ized by θ:
(t, x, y,λ) −→ ψ(0, x, y,θ):=(x, y, −cot
θ
2
), (8.2.27)
where now ψ : R
2
× S
1
−→ U(n) and we made the change of variable for real
λ = −cot (
θ
2
). Note that ψ satisfies
(u
µ
D
µ
− )ψ =0, (8.2.28)
where the operator annihilating ψ is the spatial part of the Lax pair (8.2.11),
given by
λL
0
+ L
1
1+λ
2
= u
µ
D
µ
− , where
u =
0,
1 − λ
2
1+λ
2
,
2λ
1+λ
2
=(0, −cos θ,−sin θ)
is a unit vector tangent to the t = 0 plane.
Definition 8.2.1 The matrix J satisfies the ‘trivial-scattering’ boundary condi-
tion [4, 179] if
ψ(x, y,θ) −→ ψ
0
(θ) as r −→ ∞, (8.2.29)
where ψ
0
(θ) is a U(n)-valued function on S
1
.
162 8: Symmetry reductions and the integrable chiral model
We shall now demonstrate that if J satisfies the trivial-scattering boundary
condition then ψ extends to a map from S
3
to U(n). First note that (8.2.29)
implies the existence of the limit of ψ at spatial infinity for all values of θ, while
the finite-energy boundary condition (8.2.16) only implies the limit at θ = π.
Thus the condition (8.2.29) extends the domain of ψ to S
2
× S
1
. However
(8.2.29) is also a sufficient condition for ψ to extend to the suspension SS
2
= S
3
of S
2
. This can be seen as follows. The domain S
2
× S
1
can be considered as
S
2
× [0, 1] with {0} and {1} identified. The suspension S X of a manifold X is
the quotient space [21]
SX= ([0, 1] × X)/(({0}×X) ∪ ({1}×X)).
This definition is compatible with spheres in the sense that SS
d
= S
d+1
.
Now the only condition ψ needs to fulfil for the suspension is an equivalence
relation between all the points in S
2
×{0}, since such relation for S
2
×{1} will
follow from the identification of {0} and {1}. This equivalence can be achieved
by choosing a gauge
ψ(x, y, 0) = 1. (8.2.30)
Therefore ψ extends to a map from SS
2
= S
3
to U(n) if it satisfies the zero-
scattering boundary condition. In addition, after fixing the gauge (8.2.30),
there is still some residual freedom in ψ given by
ψ −→ ψ K, (8.2.31)
where K = K(x, y,θ) ∈ U(n) is annihilated by u
µ
∂
µ
. Setting K =[ψ
0
(θ)]
−1
results in
ψ({∞},θ)=1. (8.2.32)
The gauge (8.2.32) picks a base point {x
0
= ∞} ∈ S
2
, and this implies that the
trivial-scattering condition is also sufficient for ψ to extend to the reduced
suspension of S
2
, given by
S
red
S
2
= ([0, 1] × S
2
)/(({0}×S
2
) ∪ ({1}×S
2
) ∪ ([0, 1] ×{x
0
})).
This is also homeomorphic to S
3
. The idea of (reduced) suspension is illus-
trated in (Figure 8.1).
Now let us justify the term ‘trivial scattering’ in (8.2.29). Consider equation
(8.2.28) and restrict it to a line (x(σ ), y(σ )) = (x
0
− σ cos θ, y
0
− σ sin θ),σ ∈
R on the t = 0 plane. The equation (8.2.28) becomes an ODE describing the
propagation of
ψ = ψ(x
0
− σ cos θ, y
0
− σ sin θ,θ)

8.2 Integrable chiral model 163
S
3
S
2
{1}
{0}
S
2
x [0, 1]
Figure 8.1 Suspension and reduced suspension
along the oriented line through (x
0
, y
0
)inR
2
. We can choose a gauge such that
lim
σ →−∞
ψ = 1,
and define the scattering matrix S : TS
1
→ U(n) on the space of oriented lines
in R
2
as
S = lim
σ →∞
ψ. (8.2.33)
The trivial-scattering condition (8.2.29) then implies this matrix is trivial,
S = 1. (8.2.34)
As we have explained, the boundary conditions (8.2.16) and (8.2.29) imply
that for each value of θ the function ψ extends to the one-point compact-
ification S
2
of R
2
. The straight lines on the plane are then replaced by the
great circles, and in this context the trivial-scattering condition implies that
the differential operator u
µ
D
µ
− has trivial monodromy along the compact-
ification S
1
= R ∪{∞}of a straight line parameterized by σ .
8.2.1.2 Time-dependent unitons
A general class of solutions to (8.2.13) which satisfy the trivial-scattering
boundary condition (8.2.29) is given by the so-called time-dependent unitons
J (x, y, t)=M
1
M
2
···M
m
, (8.2.35)
where the unitary matrices M
k
, k =1,...,m, are given by
M
k
= i
1 −
1 −
µ
¯µ
R
k
and R
k
≡
q
∗
k
⊗ q
k
||q
k
||
2
. (8.2.36)
Here µ ∈ C\R is a non-real constant and q
k
=(1, f
k1
,..., f
k(N−1)
) ∈ C
N
, with
k =1,...,m, are vectors whose components f
kj
= f
kj
(x
µ
) ∈ C are smooth

164 8: Symmetry reductions and the integrable chiral model
functions which tend to a constant at spatial infinity.
2
The terminology ‘trivial
scattering’ is rather confusing as solitons described by (8.2.35) do physically
scatter in R
2
if m > 1.
If m = 1 then q
1
is holomorphic and rational in
ω = µx +
1
2
µ
2
(t + y)+
1
2
(t − y)
and J is a generalization of (8.2.22) to the case n > 2. If m > 1 q
1
is still holo-
morphic and rational in ω, but q
2
, q
3
,... are not holomorphic. For m > 1the
Bäcklund transformations [35, 87] can be used to determine the q’s recursively
as we will show next.
The extended solutions corresponding to the uniton solutions (8.2.35)
factorize into the m-uniton factors
= G
m
G
m−1
··· G
1
, where
G
k
= −i
1 −
µ − µ
λ − µ
R
k
∈ GL(n, C) and R
k
=
q
∗
k
⊗ q
k
||q
k
||
2
. (8.2.37)
The exact form of q
k
’s is determined from the Lax pair (8.2.11) by demanding
that the expressions
[∂
x
− λ(∂
t
− ∂
y
)]
−1
and [(∂
t
+ ∂
y
) − λ∂
x
]
−1
(8.2.38)
are independent of λ.
Proposition 8.2.2 [35, 87] Let J : R
2,1
→ U(n) be a solution to the integrable
chiral model (8.2.13), and let
M = i
1 −
1 −
µ
¯µ
R
and R ≡
q
∗
⊗ q
||q||
2
.
Then
J = J M is another solution to (8.2.13) if the Grasmannian projector R
satisfies a pair of first-order Bäcklund relations
RL
0
|
λ=µ
(1 − R)=0 and RL
1
|
λ=µ
(1 − R)=0, (8.2.39)
where L
0
|
λ=µ
and L
1
|
λ=µ
are the Lax operators (8.2.11) evaluated at λ = µ.
Proof Let be an extended solution to the Lax pair (8.2.11) corresponding
to J which satisfies (8.2.13). Set
= G = −i
1 −
µ − µ
λ − µ
R
, so that
J =
−1
|
λ=0
= JM. (8.2.40)
2
The matrix R
k
is a Hermitian projection satisfying (R
k
)
2
= R
k
, and the corresponding M
k
is a
Grassmanian embedding of CP
n−1
into U(n). A more general class of unitons can be obtained from
the complex Grassmanian embeddings of Gr(K, n) into the unitary group. For µ pure imaginary, a
complex K-plane V ⊂ C
n
corresponds to a unitary transformation i(π
V
− π
V
⊥
), where π
V
denotes
the Hermitian orthogonal projection onto V. The formula (8.2.36) with µ = i corresponds to K =
1 where Gr(1, n)=CP
n−1
. See Appendix A for discussion of Grassmanians and their homotopy.

8.2 Integrable chiral model 165
The matrix
will be an extended solution if expressions (8.2.38) with
replaced by
are independent of λ. Set δ
0
= ∂
u
− λ∂
x
and consider the relation
(δ
0
)
−1
=(δ
0
G) G
−1
− GA
0
G
−1
where A
0
= J
−1
∂
u
J . The unitarity condition (8.2.12) holds as G(λ)G
∗
(λ)=1.
We use it to find G
−1
and equate the residue of the above expression at λ = µ
to zero. This gives
(δ
0
R)(1 − R) − RA
0
(1 − R)=0.
The identity R(1 − R) = 0 gives (δ
0
R)(1 − R)=−Rδ
0
(1 − R) and finally
R(∂
u
− µ∂
x
+ J
−1
J
u
)(1 − R)=0
which is the first relation in (8.2.39). The second relation arises in the same
way with δ
0
replaced by δ
1
= ∂
x
− λ∂
v
and A
0
replaced by A
1
= J
−1
∂
x
J . The
overdetermined Bäcklund relations (8.2.39) are compatible as J is a solution
to (8.2.13).
8.2.2 Lagrangian formulation
The Lagrangian formulation of (8.2.13) contains the Wess–Zumino–Witten
(WZW) term [19, 87]. This involves an extended field
ˆ
J defined in the interior
of a cylinder which has the 2+1 Minkowski space-time as one of its boundary
components
ˆ
J : R
2+1
× [0, 1] −→ U(n)
such that
ˆ
J (x
µ
, 0) is a constant group element, which we take to be the identity
1 ∈ U(n), and
ˆ
J (x
µ
, 1) = J (x
µ
).
The equation (8.2.13) can be derived as a stationarity condition for the
action functional
S = S
C
+ S
M
,
S
C
= −
1
2
[t
1
,t
2
]×R
2
Tr
(
J ∧∗J
)
, (8.2.41)
S
M
=
1
3
[t
1
,t
2
]×R
2
×[0,1]
Tr
ˆ
J ∧
ˆ
J ∧
ˆ
J ∧ V
.
Here ∗ is a Hodge star of η
µν
and
J = J
−1
J
µ
dx
µ
and
ˆ
J =
ˆ
J
−1
ˆ
J
p
dx
p
, where p =0, 1, 2, 3 ≡ t, x, y,ρ,
are u(n)-valued one-forms on R
2,1
and R
2,1
× [0, 1], respectively and V = 1 dx
is a constant one-form on R
2,1
× [0, 1]. We make the assumption that the
