Dunajski M. Solitons, Instantons, and Twistors

Подождите немного. Документ загружается.

126 6: Gauge ﬁeld theory

Thus the QM tunnelling between two minima q

and q

of V separated by an

energy barrier is governed by a classical gradient-ﬂow motion with a reversed

potential.

A far-reaching extrapolation of this example is that solutions of classical

equations of motion with a reversed potential (or equivalently in imagi-

nary time) are relevant in quantum ﬁeld theory. In particular the reversed

gradient-ﬂow trajectories approximate the QM tunnelling between topologi-

cally inequivalent classical vacua.

Consider the YM equation over a ‘space-time’ R

× R, with its Euclidean

metric. Let Y = R

, and let t be a local coordinate on R. The ASDYM equations

(6.4.23) can be considered as an evolution equation for a one-parameter family

of connections A(t)onY. Let A = A

dt + A. In a gauge where A

= 0 we have

∂ A

∂t

and the ASD equations (6.4.23) become

∂ A

∂t

ijk

dA(t)

= ∗

F[A(t)], (6.4.32)

where F[A(t)] is the curvature of a one-parameter family of connections A(t)

on Y, and ∗

is the Hodge operator on Y related to the Hodge operator on R

by ∗

(dt ∧ φ)=∗

φ for any one-form φ on Y. These equations can be further

rewritten in a gradient-ﬂow form

δW[A]

δA

where

W[A]=



Tr(A ∧ dA +

A ∧ A ∧ A)

is the Chern–Simons functional in three dimensions.

Now consider the Lorentzian YM equations in the temporal gauge. These

equations can be formally regarded as the motion of a particle in an

inﬁnite-dimensional space of connections on Y because the Lorentzian YM

Lagrangian is





A||

− V[A]



dt,

6.4 Yang–Mills equations and instantons 127

where the potential V[A] is given by the magnetic part of the YM curvature,

that is,

A||







x and

V[A]=



Tr(F

x =





δW

δA

δW

δA



x =

)

δW

δA

)

The analogy with classical mechanics is achieved by making the following

formal replacements:

−→ space of connections on Y

|q|

= q

−→ ||A||



Tr(A

∇−→

δA

The Euclidean YM equations correspond to a motion with a reversed poten-

tial and the gradient lines (6.4.32) of W[A] are the YM instantons – ﬁnite

action solutions to the Euclidean YM equations. The YM quantum ﬁeld theory

can be regarded as a QM on the space of connections on Y, and the QM

tunnelling takes place between different ﬂat connections on Y.

Exercises

1. Derive the Yang–Mills–Higgs equations of motion (6.3.12) from the

Lagrangian (6.3.10).

2. Show that in SU(2) Yang–Mills–Higgs theory the general solution to the

equation D

 = 0 with |

| =1is

= −ε

abc

∂



+ k



for some k

, and calculate the gauge ﬁeld corresponding to this potential.

What can you deduce about the solution of the equation D

 =0?

[Hint: Write  = ||

 and use the covariant Leibniz rule].

3. The Higgs ﬁeld

 at inﬁnity deﬁnes a map from S

to S

. In polar coordi-

nates the asymptotic magnetic ﬁeld has non-zero components:

θφ

= ε

abc

∂



∂



By writing

 = (sin ν cos µ, sin ν sin µ, cos ν),

where ν = ν(θ,φ) and µ = µ(θ,φ) show that the magnetic charge satisﬁes

g =



θφ

dθ dφ =4π deg (

).

128 6: Gauge ﬁeld theory

4. Make the ansatz



= h(r)

and A

= −ε

aij

[1 − k(r)]

and show that the Bogomolny equations for the non-abelian magnetic

monopole reduce to



= r

−2

(1 − k

) and k



= −kh.

Use the change of variables H = h + r

−1

and K = k/r to ﬁnd the one-

monopole solution (6.3.19).

5. Derive the pure SU(2) YM theory on R

from the action. Let A

(x)bea

solution to these equations. Show that



(x)=cA

(cx) is also a solution

and that it has the same action.

6. Show that any two-form F in four dimensions satisﬁes F ∧ F = ∗F ∧∗F .

7. Let A be a one-form gauge potential with values in su(2), and let F be its

curvature. Verify that Tr(A), Tr( A ∧ A), Tr( A ∧ A ∧ A ∧ A), and Tr(F )all

vanish.

8. Show that the harmonic function ρ = r

−2

in the ansatz (6.4.26) gives a pure

gauge potential and implies F =0.

The ansatz (6.4.26) with the harmonic function ρ =1+r

−2

determines a

one-instanton solution. Use the explicit integration to ﬁnd the second Chern

number of the corresponding bundle.

9. Consider the map g : S

→ SU(2) deﬁned by

g(x

, x

)=x

1+i(x

+ x

where σ

are Pauli matrices and x

+ x

= 1 and ﬁnd its degree. By

calculating Tr{[(dg) g

−1

]

} at the point on S

where x

= 1, or otherwise

deduce that the formula

deg(g)=

24π



(dg) g

−1

(

is correctly normalized.

Integrability of ASDYM

and twistor theory

The ASDYM equations played an important role in the last chapter because

of their connection with the YM instantons. In this chapter we shall explore

the integrability of these equations using the twistor methods. The twistor

transform described in Section 7.2 is a far reaching generalization of the inverse

scattering transform studied in Chapter 2. All local solutions to the ASDYM

equations will be parameterized by certain holomorphic vector bundles over a

three-dimensional complex manifold called the twistor space. Some solutions

to ASDYM can be written down explicitly as the equations can be reduced to

a linear problem. The class (6.4.26) is one example. While one cannot hope

to write the most general solution in terms of ‘known’ functions, the twistor

methods will allow to reduce the problem to a number of algebraic operations

like the Riemann–Hilbert factorization.

We shall start by introducing the Lax pair for the ASDYM equations, as it

plays a pivotal role in the twistor correspondence.

7.1 Lax pair

In this chapter we shall consider complex solutions to the ASDYM equations

on the complexiﬁed Minkowski space. Once the integrability of ASDYM is

understood in this setting, the reality conditions can be imposed.

Consider the complexiﬁed Minkowski space M

= C

with coordinates

w, z, ˜w,

z, and the metric

=2(dzd

z − dwd ˜w). (7.1.1)

The signature of the metric in C

is not well deﬁned, as it can be changed by a

complex coordinate transformation.

Let x

, x

∈ R. There are three different reality conditions one can

impose on M

which lead to R

p,q

, that is real ﬂat metrics of signature ( p, q)

with p + q =4onR

130 7: Integrability of ASDYM and twistor theory

Euclidean slice

z =

+ ix

√

z =

z,w= −

+ ix

√

, and ˜w = −

Lorentzian slice

z =

+ x

√

z =

− x

√

,w= −

+ ix

√

, and ˜w =

In the context of integrable systems it is also interesting to consider the neutral

reality conditions resulting in a real metric in (2, 2) signature. There are two

inequivalent ways to do it:

Neutral slice (a). Take z,

z,w, and ˜w ∈ R.

Neutral slice (b)

z =

+ ix

√

z =

z,w= −

+ ix

√

, and ˜w =

Choose the orientation given by the volume form

vol = dw ∧ d ˜w ∧ dz ∧ d

The two-forms

= dw ∧ dz,ω

= dw ∧ d ˜w − dz ∧ d

z, and ω

= d

z ∧ d ˜w (7.1.2)

span the space of SD two-forms. We write D

= ∂

+ A

, etc. The ASD condi-

tion (6.4.23) becomes F ∧ ω

=0,or

=0, F

w ˜w

− F

, and F

˜w

=0. (7.1.3)

The ASDYM equations arise as the compatibility condition for an overde-

termined linear system. This is an important concept which underlies the

integrability of the ASDYM (and other equations). Let us motivate it with

an example which is essentially the zero-curvature representation (3.3.10)

presented in a gauge-theoretic context.

Example. Let A

, A

be gl(2, R)-valued functions on R

which depend on

(x, y). Assume that we want to ﬁnd a two-component vector v depending on

(x, y) which satisﬁes

v := ∂

v + A

v = 0 and D

v := ∂

v + A

v =0. (7.1.4)

This is an overdetermined system as there are twice as many equations

as unknowns (the general discussion of overdetermined systems and their

solutions is given in Appendix C). The compatibility conditions com-

ing from the Frobenius theorem (Theorem C.2.5) can be obtained by

7.1 Lax pair 131

cross-differentiating

∂

v − ∂

∂

v = −∂

v)+∂

v)=(∂

− ∂

+[A

, A

])v =0

as the partial derivatives commute. Therefore the linear system (7.1.4) is

consistent iff the nonlinear equation

∂

− ∂

+[A

, A

] = 0 (7.1.5)

holds. This is just the ﬂatness F = 0 of the connection A = A

dx + A

dy,

and we could have obtained this result directly by commuting the covariant

derivatives

:= [D

, D

]=0

in (7.1.4). Let us assume that F

= 0, and let g be a fundamental matrix

solution to (7.1.4), that is, a matrix whose columns are two linearly inde-

pendent vectors satisfying (7.1.4). Then multiplying (7.1.4) by g

−1

yields the

general solution to (7.1.5)

= −(∂

g)g

−1

and A

= −(∂

g)g

−1

and A = −(dg)g

−1

is a pure gauge. Using the Jacobi identity we could show

that the calculation yields the same result (7.1.5) if solutions of (7.1.4) are in

the adjoint representation.

In Section 3.3 we have seen that many non-linear integrable equations admit a

zero-curvature representation analogous to (7.1.4). To make the whole picture

non-trivial one needs to introduce a parameter into the picture. In the case of

ASDYM equations one proceeds as follows: Consider the pair of operators

L = D

− λD

and M = D

˜w

− λD

(7.1.6)

which commute for every value of the complex spectral parameter λ ∈ CP

a consequence of ASDYM

[L, M]=F

z ˜w

− λ(F

w ˜w

− F

)+λ

=0.

Therefore the ASDYM equations arise as the compatibility condition for an

overdetermined linear system

L = 0 and M =0,

where  = (w, z, ˜w,

z,λ) is the fundamental (matrix) solution. A pair of

differential operators like (7.1.6) is called a Lax pair. Another terminology

used in Section 3.3 and due to Zaharov and Shabat is the ‘zero-curvature

representation’. This encapsulates the geometric content of (7.1.6) but is not

appropriate if L, M are operators of higher order. The existence of a Lax pair

132 7: Integrability of ASDYM and twistor theory

with a spectral parameter seems to be the key, if not the deﬁning property of

integrable non-linear PDEs.

The representation (7.1.6) can be an effective method of ﬁnding solutions if

we know (x

,λ) in the ﬁrst place. This is because the linear system

−(∂

 − λ∂

)

−1

= A

− λA

and −(∂

˜w

 − λ∂

)

−1

= A

˜w

− λA

(7.1.7)

allows to read off the components of A from the LHS. An example of this

procedure will be given in Section 8.2.1.

7.1.1 Geometric interpretation

The vectors

l = ∂

− λ∂

and m = ∂

˜w

− λ∂

(7.1.8)

span a totally null plane in M

for each value of λ in the sense that

η(l, m)=η(l, l)=η(m, m)=0

where η is the metric. There are two types of totally null planes. The classiﬁ-

cation is based on a two-form

ω = vol(l, m,...,...),

where l and m are the spanning vectors. This form must be SD or ASD in

the sense of (6.1.5) which follows from contracting ε

µναβ

with ω

µν

= l

[µ

ν]

More precisely, ∗ω is also annihilated by l, m and so is proportional to ω.

The proportionality constant must be an eigenvalue of the Hodge operator

regarded as a linear map on 

), that is, ±1. Therefore each null plane is

SD or ASD. If l and m are given by (7.1.8) then

ω(λ)=ω

+ λω

+ λ

(7.1.9)

is a linear combination of the three SD two-forms (7.1.2). The Lax pair (7.1.6)

can be expressed as

L = l + l

A and M = m + m A.

The Lax characterization of the ASDYM condition can now be summarized in

the following result.

Proposition 7.1.1 The ASDYM condition [L, M]=0on a one-form A : C

→

g ⊗ 

is equivalent to the vanishing of the YM curvature F = dA+ A ∧ Aon

each null SD two-plane.

7.2 Twistor correspondence 133

Proof This follows from the fact that [L, M] = 0 is equivalent to F (l, m)=0,

F ∧ ω(λ)=0.



This observation suggests the closer study of the space of all SD null

two-planes in the complexiﬁed Minkowski space, and underlies the twistor

approach to the ASDYM equations. We shall study this subject in the next

section.

7.2 Twistor correspondence

7.2.1 History and motivation

Twistor methods appear in various part of this book purely as a tool in solving

non-linear DEs. The original motivation behind twistor theory was rather

different and this section serves as a historical introduction to the subject. It

does not contain detailed proofs and readers interested in the applications of

twistor theory to ASDYM and other equations may skip this section at the ﬁrst

reading and go directly to Section 7.2.2.

Twistor theory was created by Roger Penrose [129] in 1967. The original

motivation was to unify general relativity and quantum mechanics in a non-

local theory based on complex numbers. Twistor theory is based on projective

geometry and as such has its roots in the nineteenth century Klein correspon-

dence. It can also be traced back to other areas of mathematics. One such

area is a subject now known as integral geometry and can be exempliﬁed by

following construction.

7.2.1.1 John transform

Let f : R

−→ R be a smooth function with suitable decay conditions at ∞

and let L ⊂ R

be an oriented line. Deﬁne a function on the space of oriented

lines in R

by v(L):=



f or

v(w, z, ˜w,

z)=



∞

−∞

f (w + s

z, z + s ˜w, s)ds (7.2.10)

where the real numbers (w, z, ˜w,

z) parameterize the four-dimensional space

M of oriented lines in R

. (Note that this parameterization misses out the

lines parallel to the plane x

= const. The whole construction can be done

invariantly without choosing any parameterization, but here we choose the

explicit approach for clarity.) The space of oriented lines is four-dimensional,

134 7: Integrability of ASDYM and twistor theory

and 4 > 3 so expect one condition on v. Differentiating under the integral sign

yields the wave equation in the neutral signature:

∂

∂w∂ ˜w

−

∂

∂z∂

=0,

and John has shown [92] that all smooth solutions to this equation arise from

some function on R

. This is a feature of twistor theory: an unconstrained

function on twistor space (which in this case is identiﬁed with R

) yields a

solution to a differential equation on space-time (in this case locally R

with a

metric of (2, 2) signature):

7.2.1.2 Penrose transform

In 1969 Penrose gave a formula for solutions to wave equation in Minkowski

space [130]:

v(x, y,ζ,t)=

2πi



⊂CP

f (−(x + iy)+λ(t − ζ ), (t + ζ )+λ(−x + iy),λ)dλ.

(7.2.11)

Here  ⊂ CP

is a closed contour and the function f is holomorphic on CP

except some number of poles. Differentiating the RHS veriﬁes that

∂

∂t

−

∂

∂x

−

∂

∂y

−

∂

∂ζ

=0.

Despite the superﬁcial similarities the Penrose formula is mathematically much

more sophisticated than John’s formula (7.2.10). One could modify a contour

and add a holomorphic function inside the contour to f without changing

the solution v. The proper description uses sheaf cohomology which considers

equivalence classes of functions and contours.

7.2.1.3 Twistor programme

Penrose’s formula (7.2.11) gives real solutions to the wave equation in

Minkowski space from holomorphic functions of three arguments. According

to the twistor philosophy this appearance of complex numbers should be

understood at a fundamental, rather than technical, level. In quantum physics

the complex numbers are regarded as fundamental: the complex wave function

is an element of a complex Hilbert space. In twistor theory Penrose aimed to

bring the classical physics at the equal footing, where the complex numbers

play a role from the start. This already takes place in special relativity, where

the complex numbers appear on the celestial sphere visible to an observer on a

night sky. This is a t = const section of observer’s past null cone.

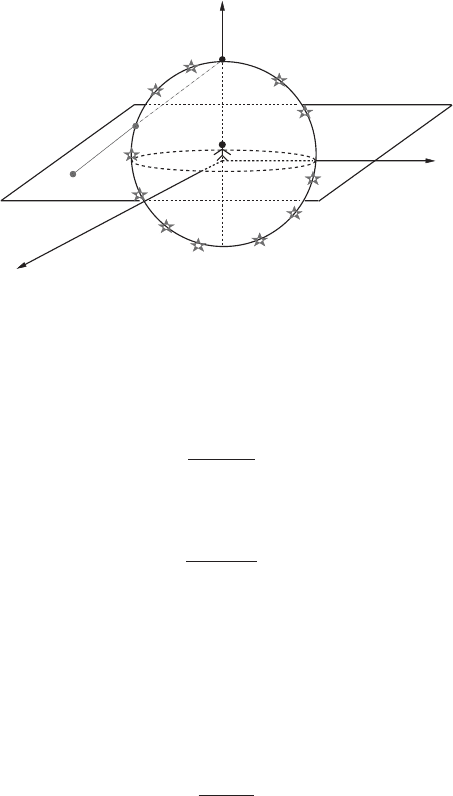
7.2 Twistor correspondence 135

N ⫽ (0, 0, 1)

Stereographic projection from the

celestial s

here

)

⫹ (u

)

⫹ (u

)

⫽1

The two-dimensional sphere is the simplest example of a non-trivial complex

manifold (see Appendix B for more details). Stereographic projection from the

north pole (0, 0, 1) gives a complex coordinate

λ =

+ iu

1 − u

Projecting from the south pole (0, 0, −1) gives another coordinate

λ =

− iu

1+u

On the overlap

λ =1/λ. Thus the transition function is holomorphic and

this makes S

into a complex manifold CP

(Riemann sphere). The double-

covering SL(2, C)

2:1

−→ SO(3, 1) can be understood in this context. If world-

lines of two observers travelling with relative constant velocity intersect at a

point in space-time, the celestial spheres these observers see are related by a

Möbius transformation

λ →

αλ + β

γλ+ δ

where the unit-determinant matrix



αβ

γδ



∈ SL(2, C)

corresponds to the Lorentz transformation relating the two observers.

The celestial sphere is a past light cone of an observer O which consist of

light rays through an event O at a given moment. In the twistor approach

the light rays are regarded as more fundamental than events in space-time.

The ﬁve-dimensional space of light rays PN in the Minkowski space is a