Dunajski M. Solitons, Instantons, and Twistors
Подождите немного. Документ загружается.

96 5: Lagrangian formalism and field theory
5.3.1 Topology and Bogomolny equations
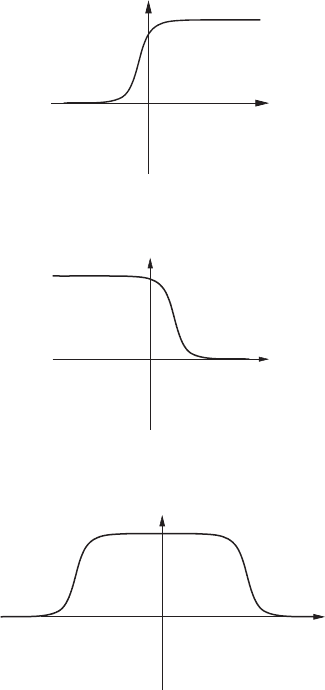
All finite energy field configurations approach vacuum at ±∞. Asymptotic
values cannot change (Figures 5.2–5.4). Topological conserved currents are
properties of a finite energy continuous field. For (5.2.13) with D = 1 topolog-
ical conserved quantities are
φ
−
= lim
x→−∞
φ and φ
+
= lim
x→∞
φ.
If φ
+
= φ
−
then the field φ(x) can be continuously deformed into the zero-
energy vacuum φ = φ
+
. If on the other hand φ
+
= φ
−
then φ cannot be continu-
ously deformed into a vacuum, which is the reason for topological stability of
kinks.
x
Figure 5.2 Kink, N =1
x
Figure 5.3 Anti-kink, N = −1
x
Figure 5.4 Kink–anti-kink pair, N =0
5.3 Scalar kinks 97
The associated conserved current
N = φ
+
− φ
−
=
R
φ
x
dx
is an integral of a total derivative which depends only on boundary conditions.
It is conserved because we insisted on the finiteness of the energy. Note that
the field equations have not entered the discussion at this stage. Topological
conserved currents are in this sense different from the Noether currents which
result from continuous symmetries of the Lagrangian.
We shall look for minimal energy configurations. If U ≥ 0 we can always
find W(φ) such that
U(φ)=
1
2
dW(φ)
dφ
2
.
Now
E =
1
2
R
dx(φ
2
t
+ φ
2
x
+ W
2
φ
)=
1
2
R
dx
%
φ
2
t
+(φ
x
± W
φ
)
2
∓ 2φ
x
W
φ
&
=
1
2
R
dx
%
φ
2
t
+(φ
x
± W
φ
)
2
&
∓ [W(φ(∞)] − W[φ(−∞)].
Therefore
E ≥|W [φ(∞)] − W [φ(−∞)]|. (5.3.20)
This is the Bogomolny bound. It depends only on the topological data at ±∞.
Say
φ(∞)=φ
2
>φ(−∞)=φ
1
.
The minimum energy configurations satisfy φ
t
= 0 (the static condition), E =
W(φ
2
) − W(φ
1
) and
dφ
dx
=
dW
dφ
(5.3.21)
which is the Bogomolny equation. Its solutions are kinks (5.3.18).
The field equation (5.3.17) is a second-order PDE, and its special solutions
arise form the first-order ODE (the Bogomolny equation). A time-dependent
solution to (5.3.17) can be found by the Lorentz boost. In general (any dimen-
sion and Lagrangian) the full field equations are usually not integrable, but the
Bogomolny equations are often integrable (and have lower order).
r
Example. U = λ
2
(φ
2
− a
2
)
2
/2 gives W = λ(a
2
φ − φ
3
/3). The Bogomolny
equations (5.3.21) yield
φ
x
= λ(a
2
− φ
2
),

98 5: Lagrangian formalism and field theory
and φ is the static kink solutions (5.3.19) with energy
E = W(a) − W(−a)=
4
3
λa
3
.
This kink is stable as it would take infinite energy to change this solution
into a constant vacuum solution φ = 0. In general kinks minimize the energy
within their topological class. The absolute minimum is of course 0 which
corresponds to φ
1
= φ
2
.
r
Example. U =1− cos βφ. This theory has infinitely many vacua,
φ
n
=
2πn
β
,
parameterized by n ∈ Z, and kinks interpolate between adjacent vacua. The
field equation (5.3.17) is the Sine-Gordon equation.
φ
tt
− φ
xx
+ β sin βφ = 0 (5.3.22)
which is essentially equivalent to (2.1.2) as the parameter β can be set to 1
by scalings of (x, t,φ).
The kink solution with φ(−∞)=0,φ(∞)=2π/β is given by
φ =
4
β
arctan
−1
e
β(x−x
0
)
.
The solution is multivalued and we get all possible kinks depending on which
branch we choose. In this case time-dependent solutions to the full equations
(multi-kinks and solitons) can be constructed using the integrability of the
Sine-Gordon equation. The simplest solution generating technique is the
Bäcklund transformation described in Section 2.1.2.
The Sine-Gordon equation admits time-dependent solutions such that φ
tends to the same limit at ±∞. These so-called breathers have trivial topolog-
ical charge and owe their stability to the complete integrability of (5.3.22),
and the existence of an infinite number of conservation laws preventing
annihilation into radiation. By contrast U = λ
2
(φ
2
− a
2
)
2
/2 does not posses
such solutions, as the corresponding field equations are not integrable.
5.3.2 Higher dimensions and a scaling argument
Can there exist finite-energy static critical points of (5.2.12) in more than
one spatial dimension? In this section we shall examine a scaling argument,
originally due to Derrick [37] and rule out all dimensions higher than 2. In
Section 6.1.1 we shall return to Derrick’s argument in the context of gauge
theory where the spatial dimensions three and four are also allowed.
5.3 Scalar kinks 99
If φ(x) is a static solution to (5.2.13) in D spatial dimensions, then
∇
2
φ =
dU
dφ
,
and φ is a critical point of the energy functional
E(φ)=
R
D
d
D
x
1
2
|∇φ|
2
+ U(φ)
= E
grad
+ E
U
.
Consider a one-parameter family of configurations φ
(c)
(x)=φ
(1)
(cx), where
φ
1
(x) is a static finite-energy solution. Then
E[φ
(c)
]=
1
c
D−2
E
grad
+
1
c
D
E
U
.
Since E(φ
1
) is a minimum of E we have
dE[φ
(c)
]/dc|
c=1
=0
which implies
(D − 2)E
grad
+ DE
U
=0. (5.3.23)
D = 1. Static solutions are possible with E
grad
= E
U
. These are the kinks
(5.3.21).
D = 2. Static solutions are possible with E
U
= 0. This can still lead to non-
linear field theories if the target space is a manifold without a linear
structure, φ : R
2+1
→ . These so-called sigma models will be studied in
Section 5.4.
D = 3. Finite-energy static solutions do not exist. Adding a Skyrme term
|∇φ|
4
to the Lagrangian density allows static solutions via the scaling
argument. See [114] for a complete discussion of the Skyrme model.
Although the D = 1 kinks do not generalize to solitons in D > 1, they can
be trivially lifted to translationally invariant solutions of scalar field theory
(5.2.13) in any dimension. These lifted solutions have infinite energy as a result
of the integration along the (D − 1) spatial directions on which the kinks do
not depend. The energy is however finite per unit volume. This type of solution
is called a domain wall. Finally we note that the Derrick argument breaks down
for time-dependent configurations.
5.3.3 Homotopy in field theory
Any static, smooth field configuration φ : R
D+1
−→ R
N
is topologically trivial,
as it can be transformed to zero by a homotopy (1 − τ )φ (see Appendix A for
discussion of homotopy). Non-trivial field configurations appear if we assume

100 5: Lagrangian formalism and field theory
that the energy density
E =
1
2
∇φ
a
·∇φ
a
+ U(φ
1
,...,φ
N
)
of a static field decays as r −→ ∞. This condition alone does not necessarily
lead to finite energy, but it gives rise to a topological classification. Let M ⊂ R
N
be a submanifold of the target space implicitly defined by
U(φ
1
,...,φ
N
)=U
mi n
,
where U
mi n
is the minimal value of U. At spatial infinity φ = φ
∞
must take its
values in M, or the density E will not vanish. Therefore
φ
∞
: S
D−1
−→ M,
and smooth field configurations are classified by elements of the homotopy
group π
D−1
(M).
Later we will meet other ways of classifying smooth field configurations: In
sigma models U = 0, and φ : R
D+1
−→ . Fields are classified by elements of
π
D
() as any static field with finite E must smoothly extend to the one-point
compactification S
D
of R
D
. In pure gauge theories gauge fields are classified by
Chern numbers which arise from integrating various powers of the field tensor.
This will be discussed in Section 6.4. Finally in gauge theories with Higgs fields,
the Higgs fields at infinity carry all topological information (see Section 6.3.1).
5.4 Sigma model lumps
Sigma models are non-linear in a fundamental way: the target space is not a
linear space. Consider a field φ : R × R
2
−→ S
N−1
, with components φ
a
(x
µ
) ∈
R
N
which satisfy the non-linear relation
N
a=1
φ
a
φ
a
=1. (5.4.24)
The kinetic Lagrangian density
L =
1
2
∂
µ
φ
a
∂
µ
φ
a
gives rise to a non-linear equation. To see this introduce a Lagrange multiplier
λ(x
µ
), and consider the Euler–Lagrange equations of
L
= L − (1/2)λ(x
µ
)(1 −
φ
a
φ
a
).

5.4 Sigma model lumps 101
This yields
φ
a
− λφ
a
=0, where = η
µν
∂
µ
∂
ν
,
and the constraint (5.4.24). Multiplying the relation above by φ
a
, summing
over a, and eliminating λ yield the non-linear field equations
φ
a
− (φ
b
φ
b
)φ
a
=0. (5.4.25)
The Lagrangian and the equation (5.4.25) are invariant with respect to global
O(N) rotations of the field φ. This is an example of a model with an internal
symmetry.
Solving the constraint (5.4.24) yields φ
N
= ±
1 − φ
p
φ
p
, where p, q, r =1,
...,N − 1, and allows us to write the Lagrangian density as
L =
1
2
g
pq
(φ)η
µν
∂
µ
φ
p
∂
ν
φ
q
, (5.4.26)
where
g
pq
= δ
pq
+
φ
p
φ
q
1 −
φ
r
φ
r
is the metric on S
N−1
induced by the Euclidean inner product in R
N
. Lagrange
densities of the form (5.4.26) where η and g are arbitrary metrics on a space
time and a target space, respectively, define more general sigma models. For
example, superstring theory can be viewed as a sigma model where η is a
metric on a ‘string world-sheet’ which is a Riemann surface, and g is a metric
on a 10-dimensional target which plays the role of ‘space time’.
From now on we restrict our attention to (5.4.25) with N = 3. The corre-
sponding model describes the Heisenberg ferromagnet in low temperatures,
when the local magnets line up [66]. The system is characterized by the
direction of the spin vector, that is, a unit vector φ
a
.
We will be interested in time-independent solutions with a finite-energy func-
tional
Ld
2
x. This condition implies that r|∇φ
a
|→0asr →∞, therefore
φ(x
i
) tends to a constant field φ
∞
at spatial infinity, which we choose to be the
north pole (0, 0, 1). This means that the finite-energy static solutions extend
1
to S
2
. This sphere has infinite radius, and is a one-point compactification of
R
2
. The Laplacian in two dimensions is conformally invariant is the sense
that
c
cg
=
g
1
This is not strictly true, as the finiteness of the L
2
norm of ∇φ does not imply that ∇φ −→ 0.
There could exist finite-energy maps which do not extend to S
2
. Sacks and Uhlenbeck [143]
show that this does not happen. Their proof uses the equations of motion and their conformal
invariance.

102 5: Lagrangian formalism and field theory
for two conformally related metrics g and c(x
i
)g. This can be verified from the
definition
g
= |g|
−1/2
∂
i
(|g|
1/2
g
ij
∂
j
).
Therefore the static equations
φ
a
− (φ
b
φ
b
)φ
a
= 0 (5.4.27)
are satisfied on S
2
.
Another consequence of the conformal invariance is that the spatial rescaling
does not change the energy, and can be used to shrink any static solution down
to zero. Therefore the solitons we are just about to describe do not fully deserve
their name, and are called lumps by some authors.
Continuous maps φ : S
2
−→ S
2
are classified by their topological degree (in
this context also called topological charge) given by (A7)
Q = deg φ =
1
8π
S
2
ε
ij
ε
abc
φ
a
∂
i
φ
b
∂
j
φ
c
d
2
x
which partially characterizes static solutions. A field with a given Q cannot be
continuously deformed into a field with different Q. It is now clear why we
have focused on N = 3. The spheres with N > 3 as target spaces would not
lead to non-trivial topological configurations, as the relevant homotopy group
π
2
(S
N−1
) vanishes.
The degree Q carries only global information and fields can have different
energies within one topological sector.
Proposition 5.4.1 The energy
E =
1
2
S
2
∂
i
φ
a
∂
i
φ
a
d
2
x ≥ 4π|Q| (5.4.28)
is bounded from below with equality when the first-order Bogomolny
equations
∂
i
φ
a
= ±ε
ij
ε
abc
φ
b
∂
j
φ
c
(5.4.29)
are satisfied.
Proof 1 Consider the identity
(∂
i
φ
a
± ε
ij
ε
abc
φ
b
∂
j
φ
c
)(∂
i
φ
a
± ε
ij
ε
abc
φ
b
∂
j
φ
c
)d
2
x ≥ 0
and use the relations
ε
ij
ε
ik
= δ
jk
,ε
abc
ε
ade
= δ
bd
δ
ce
− δ
be
δ
cd
, and φ
a
∂
j
φ
a
=0
to deduce (5.4.28) and (5.4.29).

5.4 Sigma model lumps 103
The solutions to the Bogomolny equations (5.4.29) are critical points of the
energy functionals, and so are also solutions to the second-order static-field
equations (5.4.27). It can be shown [166] that all finite-energy solutions to
(5.4.27) are solutions to the Bogomolny equations. In the context of the
Heisenberg ferromagnet the solutions of (5.4.29) are called spin waves. The
degree of φ describes how often the spins aligned along some axis twist around
this axis. More generally, the degree can be interpreted as the number of lumps,
because generically the energy density is concentrated in Q localized regions.
The Bogomolny equations (5.4.29) can be easily solved with the help of
complex numbers. Identify S
2
with a complex projective line CP
1
(the cor-
responding model is sometimes called the CP
1
model, or O(3) model). Let
f : R
2,1
−→ CP
1
be given by
φ
1
+ iφ
2
=
2 f
1+| f |
2
and φ
3
=
| f |
2
− 1
| f |
2
+1
, so that f =
φ
1
+ iφ
2
1 − φ
3
.
(5.4.30)
The Bogomolny equations now imply that f is holomorphic, or anti-
holomorphic in z = x
1
+ ix
2
. The total energy (5.4.28) of static fields in terms
of f is given by
E =
1
4
S
2
df ∧ df
(1 + | f |
2
)
2
and the rational function
f = c
(z − p
1
) ···(z − p
Q
)
(z − r
1
) ···(z −r
Q
)
,
gives finite-energy solutions which saturate the Bogomolny bound with
deg(φ)=Q. This is because only the rational functions give Q-fold coverings
of an extended complex plane with finite Q. The overall factor c can be set to 1
by a global rotation of the field. The space of static solutions is isomorphic to
the space-based rational maps because lim
z→∞
φ = φ
∞
. It is the complement in
C
2Q
of a hypersurface where the enumerator and denominator have common
poles.
Exercises
1. Starting with the Lagrangian of the Sine-Gordon theory
L =
1
2
(φ
2
t
− φ
2
x
) − (1 − cos βφ)

104 5: Lagrangian formalism and field theory
derive the Sine-Gordon equation. Find a kink solution of the Sine-Gordon
theory, and use the Bogomolny bound to find its energy. How many types
of kinks are there?
2. The Sine-Gordon equation is
φ
xx
− φ
tt
=sinφ, where φ = φ(x, t).
Set τ =(x + t)/2,ρ =(x − t)/2 and consider the Bäcklund transformations
∂
ρ
(φ
1
− φ
0
)=2b sin
φ
1
+ φ
0
2
and ∂
τ
(φ
1
+ φ
0
)=2b
−1
sin
φ
1
− φ
0
2
,
where b = const and φ
0
,φ
1
are functions of (τ,ρ). Take φ
0
= 0 and construct
the one-soliton (kink) solution φ
1
.
3. Let φ = φ(x, t) be a scalar field and let U = U(φ) ≥ 0. Define the energy of
solutions to the Euler–Lagrange equations with the Lagrangian density
L =
1
2
φ
2
t
−
1
2
φ
2
x
− U(φ).
Assume that U =(1/2)φ
2
(φ
2
− β
2
)
2
, where β ∈ R. How many static kink
solutions are there? Find a moving kink solution for the model if β =0.
4. The Lagrangian density for a complex scalar field φ on the two-dimensional
Minkowski space R
1,1
is
L =
1
2
|φ
t
|
2
−
1
2
|φ
x
|
2
−
1
2
λ
2
(a
2
−|φ|
2
)
2
, a ∈ R.
Find the field equations, and verify that the real kink φ
0
(x)=a tanh (λax)
is a solution. Now consider a small pure imaginary perturbation φ(x, t)=
φ
0
(x)+iη(x, t) with η real and find the linear equation satisfied by η.
By considering η =sech (αx)e
ωt
show that the kink is unstable.
5. Let φ : R
2,1
→ S
2
. Set
φ
1
+ iφ
2
=
2 f
1+| f |
2
and φ
3
=
| f |
2
− 1
| f |
2
+1
,
and deduce that the Bogomolny equations
∂
i
φ
a
= ±ε
ij
ε
abc
φ
b
∂
j
φ
c
and φ
t
=0
imply that f is holomorphic or anti-holomorphic in z = x
1
+ ix
2
. Find an
expression for the total energy
E =
1
2
∂
j
φ
a
∂
j
φ
a
d
2
x
in terms of f .

6
Gauge field theory
In Chapter 5 we have given examples of Lagrangians invariant under the action
of symmetry groups. These symmetry transformations were identical at every
point of space time. This is referred to as global symmetry in the physics
literature. In this chapter we shall introduce a concept of gauge symmetry,
where the symmetry transformation is allowed to depend on a space-time
point. This is what physicists call local symmetry. This type of symmetry
is already present in Maxwell’s electrodynamics. The kinetic term i
ψγ
µ
∂
µ
ψ
in the Lagrangian involving the matter field (electron) ψ is unchanged if we
replace ψ by e
ieθ
ψ, where e is the electric charge of an electron and γ
µ
are the
Dirac matrices. If θ is a constant, we talk about global symmetry. Gauging, or
localizing, this symmetry comes down to allowing θ = θ(x
µ
). The Lagrangian
is no longer invariant, unless we replace the ordinary derivative ∂/∂x
µ
by a
covariant derivative D
µ
= ∂
µ
− ie A
µ
, where the gauge potential A
µ
transforms
as A
µ
→ A
µ
+ ∂
µ
θ.
The matter Lagrangian is then complemented by adding a gauge term
−(1/4)F
µν
F
µν
where F
µν
= ∂
µ
A
ν
− ∂
ν
A
µ
is the gauge field. The whole
Lagrangian is invariant under the local gauge transformations and the gauge
potential is promoted to a dynamical variable. It corresponds to a gauge boson
which in the case of electrodynamics is identified with a photon. The symmetry
group which has been gauged in this example is U(1). Thus electrodynamics
is a U(1) gauge theory. The abelian nature of U(1) implies that there are no
interactions between the photons.
The breakthrough made by Yang and Mills [188] was to replace U(1) by a
non-abelian Lie group G. In the gauging process one needs to introduce one
gauge boson for each generator of G. The bosons are particles which ‘carry
interactions’ between the matter fields, and the form of the interactions is
dictated by the gauge symmetry. The bosons take values in the Lie algebra of G.
If G = SU(3) there are eight gauge bosons generalizing one photon. They
are called gluons. The matter fields generalizing the electron are called quarks.
The quarks are charged with colour, which generalizes the electric charge. The
quantum SU(3) gauge theory is called quantum chromodynamics (QCD). It is
a theory of strong nuclear interactions.
