Духин А.А. Теория информации

Подождите немного. Документ загружается.

131

§ 1.

ЗАДАЧИ

ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ.

ОСНОВНЫЕ

ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ

столбцов матрицы Н. Наоборот, каждому соотношению

линейной зависимости, включающему d столбцов матрицы

Н, соответствует кодовое слово веса d.

Доказательство. Вектор a = (a

..,a

) является кодовым словом тогда и

только тогда, когда

аН

=0.

(4.15)

Обозначим hf - i -й столбец матрицы Н.

Соотношение (4.1.5) можно переписать в иной форме:

А . (4-1-6)

i=l

Соотношение (4.1.6) линейной зависимости связывает столбцы матрицы Н .

Число столбцов матрицы, которые входят с ненулевыми коэффициентами, рав-

но d - числу ненулевых компонент вектора а. Это число равно весу а:

W(a) = d.

С другой стороны, коэффициенты любого соотношения линейной зависи-

мости, связывающие столбцы матрицы Н, являются компонентами вектора,

который должен принадлежать ортогональному пространству матрицы Н . А

Следствие. Блоковый код, являющийся ортогональным пространством мат-

рицы Н, имеет минимальный вес (и, следовательно, кодовое расстояние), рав-

ный самое меньшее d, тогда и только тогда, когда любая совокупность (d -1)

и меньшего числа столбцов матрицы Н является линейно независимой.

Определение 1.7. Вероятностью ошибки декодирования для дан-

ной схемы декодирования называется вероят-

ность появления кодового слова на вы-

ходе декодера, отличного от передан-

ного в канал связи.

В предположении, что все кодовые слова используются с равной вероят-

ностью:

—гУ]р

{выход декодера

gj / g

- послано}. (4.1.7)

Ч i»i

Для любого канала с независимыми ошибками два кода, отличающиеся

только расположением символов, имеют одну и ту же вероятность ошибки р

132

ГЛАВА

IV. ЛИНЕЙНЫЕ КОДЫ, ИСПРАВЛЯЮЩИЕ

ОШИБКИ

Определение 1.8. Коды, отличающиеся перестановкой столбцов в

порождающей матрице, называются эквива-

лентными.

Если G

~ линейный код с порождающей матрицей G

то код G

эквива-

лентен коду G, тогда и только тогда, когда порождающая матрица G

может

быть получена из матрицы G

{

перестановкой столбцов.

Назовём две порождающие матрицы комбинаторно-эквивалентными, если

одна из другой может быть получена путём элементарных преобразований

строк и перестановкой столбцов.

Определение 1.9. Линейный (n,k)-код G называется система-

тическим, если первые к компонент каждого

кодового слова являются информационными

символами, а последние n-к компоненты -

проверочными символами.

Порождающая матрица G систематического

(п,

к)-кода имеет вид:

Pllv«»Pi,n-k

(4.1.8)

•|Pkl»->Pk,n-k )

Матрица вида (4.1.8) называется приведённой.

Теорема 1.1. Каждый линейный

(п,к)-ко<3

эквивалентен систематичес-

кому коду.

Доказательство. Рассмотрим (п,к)-код с порождающей матрицей G. Про-

ведём следующие преобразования строк G .

Поскольку строки матрицы G линейно независимы, то в i -й строке

найдётся, по меньшей мере, один ненулевой элемент. Пусть первый

отличный от нуля элемент находится в j-м столбце ау*0. Разделим

каждый элемент i -й строки на <Хц. После этого преобразования элемент в

i-й строке и j-м столбце матрицы станет равным 1.

133

§ t. ЗАДАЧИ

ПОМЕХОУСТОЙЧИВОГО

КОДИРОВАНИЯ.

OCHQBI

IUE

ОПРЕДЕЛЕНИЯ

ПОНЯТИЯ

К каждой

1-VL

строке (£Ф\) прибавим i-ю строку, умноженную на

(~а.ц).

В результате в j-м столбце матрицы будут нули, кроме i-й компоненты,

равной единице.

Эти преобразования, совершённые с каждой строкой матрицы G, приводят

к матрице С, содержащей к столбцов, состоящих из (к-1) нуля и одной

единицы. Отметим, что матрицы G и G' являются порождающими матрица-

ми одного кода.

Перестановкой столбцов сгруппируем слева к столбцов, содержащих еди-

ницы так, чтобы они образовывали единичную матрицу (kxk). В результате

получим комбинаторно эквивалентную матрицу G" следующего вида:

G" =(Е

|р)=

Pll>~,Pi,n-k

(4.1.9)

l|Pklv«,Pk,n-k

Пусть a =(ai

..,aj

) - вектор с произвольными компонентами из GF(q).

Составим линейную комбинацию g строк матрицы G", используя в качестве

коэффициентов компоненты ai,...,ak:

g = (a! ,.-.,a

, Y!Y

-k ), (4.1.10)

где Yj =

][]

iPij'

j =

l,...,n-k.

i=l

Следовательно, если G" - порождающая матрица кода G", то g - кодовое

слово. Таким образом, первые к компонент кодового вектора могут быть

произвольно выбранными информационными символами, а каждая из послед-

них n - к компонент представляет собой линейную комбинацию к первых из

них. Построенный код G" является систематическим. А

Если порождающая матрица кода имеет приведённую форму, то одна из

проверочных матриц может быть легко найдена.

Теорема 1.2. Если G - систематический код с порождающей матрицей

|p],

- единичная матрица порядка (kxk), а

Р - матрица порядка (kx(n-k)), то проверочная мат-

рица Н имеет вид:

Н = [-Р

|Е„_

]. <

134

ГЛАВА

IV. ЛИНЕЙНЫЕ КОДЫ, ИСПРАВЛЯЮЩИЕ

ОШИБКИ

Доказательство

теоремы осуществляется непосредственной проверкой. •

Пример

1.3. Для кода, рассмотренного в примере 1.2, в качестве порождаю-

щей матрицы была приведена матрица следующего вида:

100

010

001

iOl

«(E,|P).

В силу теоремы

4.1.2

поверочной матрицей кода будет:

по

101

)

Все введённые определения и понятия будут использованы в последующих

параграфах настоящей главы и в заключительной главе в теоремах кодиро-

вания.

§2

Как следует из лемм 4.1.1 и 4.1.2, способность кода корректировать ошибки

находится в прямой зависимости от величины кодового расстояния - хорошие

корректирующие свойства обеспечиваются большим кодовым расстоянием и

наоборот. Для построения кодов с большим кодовым расстоянием требуется

вводить много проверочных символов, не передающих информацию от источ-

ника к адресату, а выполняющих вспомогательную роль. Наличие большого

числа проверочных символов при фиксированной длине кодового слова умень-

шает число информационных символов, а следовательно, и скорость передачи

информации

Таким образом, хорошие корректирующие свойства кода и высокая скорость

передачи информации - требования противоречивые. Поэтому задача построе-

ния кодов с приемлемыми значениями d и R - задача оптимизации, не имею-

щая единственного решения. Параметры n,k,d, характеризующие код, не мо-

гут принимать произвольных значений. Нетрудно видеть, что:

- среди кодов с одинаковыми параметрами пик лучшим является код, ко-

торый имеет больше кодовое расстояние d,

- среди кодов с одинаковыми параметрами п и d лучшим является код, ко-

торый имеет большее число информационных символов к,

- среди кодов с одинаковыми параметрами к и d лучшим является код, ко-

торый имеет меньшую длину п, а следовательно, и меньшее число прове-

рочных символов.

Между рассмотренными параметрами n,k,d существуют определённые

соотношения, задаваемые границами для кодового расстояния или для скорос-

ти передачи информации. Различают верхние и нижние границы; некоторые

из них будут рассмотрены в настоящем параграфе.

Теорема 2.1 (Верхняя граница Хемминга). Если существует линейный

q-чный код G с длиной блока n,k информационными сим-

волами и

кодовым,

расстоянием d = 2t

+1,

то:

n-k

(4.2.1)

ГРАНИЦЫ ДЛЯ ПАРАМЕТРОВ КОДОВ

136

ГЛАВА

IV.

ЛИНЕЙНЫЕ

КОДЫ,

ИСПРАВЛЯЮЩИЕ

ОШИБКИ

Доказательство. Для каждого geG рассмотрим следующее множество

D(g)cV

(GF(4)):

D(g) = (Г

й(1,Г)

* «,Г € V

(GF(*))}. (4.2.2)

Множество D(g) включает все последовательности ~g\ отличающиеся от

g не более чем в t компонентах. Число таких последовательностей длины п,

входящих в D(g), равно:

<?"1) • (4.2.3)

'№)]= Z

Так как по условию доказываемой теоремы множества D(g), соответствую-

щие различным кодовым словам, не имеют общих элементов, и число их сов-

падает с числом кодовых слов, то:

](?-D^?

i=0

Отсюда следует справедливость теоремы. •

Для двоичного случая (q = 2) соотношение (4.2.1) можно переписать так:

В формуле (4.2.1) равенство достигается в том случае, когда <?

|D(g)| = <?

Геометрически это означает, что непересекающиеся шары, проведённые вок-

руг точек, задаваемых кодовыми словами g

,...,g ь , заполняют всё векторное

пространство V

(GF(?)), и при этом каждый вектор из V

оказывается в од-

ной из сфер.

Определение

2.1.

Коды, для которых выполняется равенство

\(q-l)

, называются совершен-

1=0 <

ными или плотно упакованными.

Тривиальным примером такого кода является код кратных повторений.

Другие примеры будут даны ниже.

137

§ 2. ГРАНИЦЫ ДЛЯ ПАРАМЕТРОВ КОДОВ

Теорема

2.2 (Верхняя граница Плоткина). Если существует q-чный бло-

ковый код длины п с общим числом кодовых слов М и ко-

довым расстоянием d, то:

q(M-l)

(

)

Доказательство.

Оценка (4.2.5) получается в результате оценки сверху

среднего расстояния между кодовыми словами. Пусть

G=(g

Обозначим у

* - m-ю компоненту i -го кодового слова. Для определения

среднего расстояния подсчитаем сумму D всевозможных попарных расстоя-

ний между кодовыми словами:

ММ/

v М М п / ч

D = ZZd(g«;g^)=XZZdfe

)

»^

)

i=l j=l i=l j=l m=l

Меняя порядок суммирования, получаем:

n М М / ч

D-ZSZ

frM

}

(4.2.6)

Обозначим у

число символов, равных i среди компонент

Ут^—^Ут

У«*0>

Ху|„=М,

yj^N + O.

Имеет место:

т 14 / ч ч Ч

i=i j=i i=i

= (y!nv.,y^) (1-Е)

|УтУт

(4.2.7)

i=i j=i

F(y,y),

где 5ц =

0 i = j

[1 i*j

единичная матрица (qxq)

, I - матрица (q x q), состоящая из единиц, E -

138

ГЛАВА

IV.

ЛИНЕЙНЫЕ

КОДЫ, ИСПРАВЛЯЮЩИЕ

ОШИБКИ

Для оценки сверху условного максимума квадратичной формы

F(y,y), за-

висящей

от

неотрицательных целочисленных аргументов, удовлетворяющих

уравнениям связи, найдём методом Лагранжа максимум квадратичной формы

F(x,x),

где xeR

Естественно,

что

max F(y, у) < max F(x,

х).

С использованием индукции

по q

покажем,

что

max F(x,x) =

M^-l)

когда

> 0,

У^х

;

= М .

Если

q = 2, то

F(x,x) = (x„x

\10Дх

= 2x^2,

+х

=М, х

>0, х

>0.

Составим функцию Лагранжа:

Ф(х

;Х) = 2x^

-A,(x

+х

Найдём частные производные:

—

2х

-Х,

9х

Решая систему:

Г2х

-Х = 0,

[2xj -А, = 0,

находим,

что

точка условного максимума

(х^х

) =

щее значение квадратичной формы равно

М М

maxF(x,x) =

Пусть

для q-1

справедливо утверждение:

(4.2.8)

а соответствую-

яцс

F|(x, );(xj

,.»,х„_1

)j= ^ . (4.2.9)

139

- ГРАНИЦЫ ДЛЯ

ПАРАМЕТРОВ

КОДОВ

Покажем справедливость (4.2.8). Составим функцию Лагранжа

ij i=l

и вычислим частные производные:

дФ(х

...,х ;Х) я

S8ijXj-A.=:0,

l<i<

Составим систему уравнений:

+х

+... +

Х0_!

+ x

|xi+ х

+ ... + х^х+

[Х\

+ х

+ ...

„i + =Х.

Складывая уравнения системы, получаем:

1=1

Вычитаем из полученного соотношения i-e уравнение системы:

.Ч. X

-1)Х-

1,...,?.

q-l

Из (4.2.10) и уравнения связи имеем:

М;?1 =

М(9

(4.2.10)

(4.2.11)

<?-!

' ? (

-2-12)

Подставляя (4.2.12) в выражение (4.2.11), получаем координаты стационар-

ной для Ф(х;Х) точки:

М М

Я ' Я j

этой точке значение квадратичной формы F(x,x) равно М

<?-*

Так как рассматриваемая область значений переменных является ограни-

ченной и замкнутой, то экстремум F(x,x) достигается либо на границе, либо

в стационарной точке. На границе области по крайней мере одна из перемен-

ных обращается в нуль. Следовательно, мы оказываемся в условиях индуктив-

ного предположения. При этом:

max

F((X,

,...,x

y,ix

,...,\

_i))=

MJi_J)

140

ГЛАВА IV. ЛИНЕЙНЫЕ К ОДЫ,

ИСПРАВЛЯЮЩИЕ

ОШИБКИ

Следовательно:

Так как число различных пар кодовых слов равно М

- М, то:

Из сравнения левой и правой частей получаем доказательство теоремы. А

Определение 2.2. Коды, для которых нестрогое неравенство

(4.2.5) обращается в равенство, называются

эквидистантными.

Обращение в равенство (4.2.5) означает, что расстояние между двумя лю-

быми кодовыми словами одинаково. Это обстоятельство объясняет введённый

выше термин.

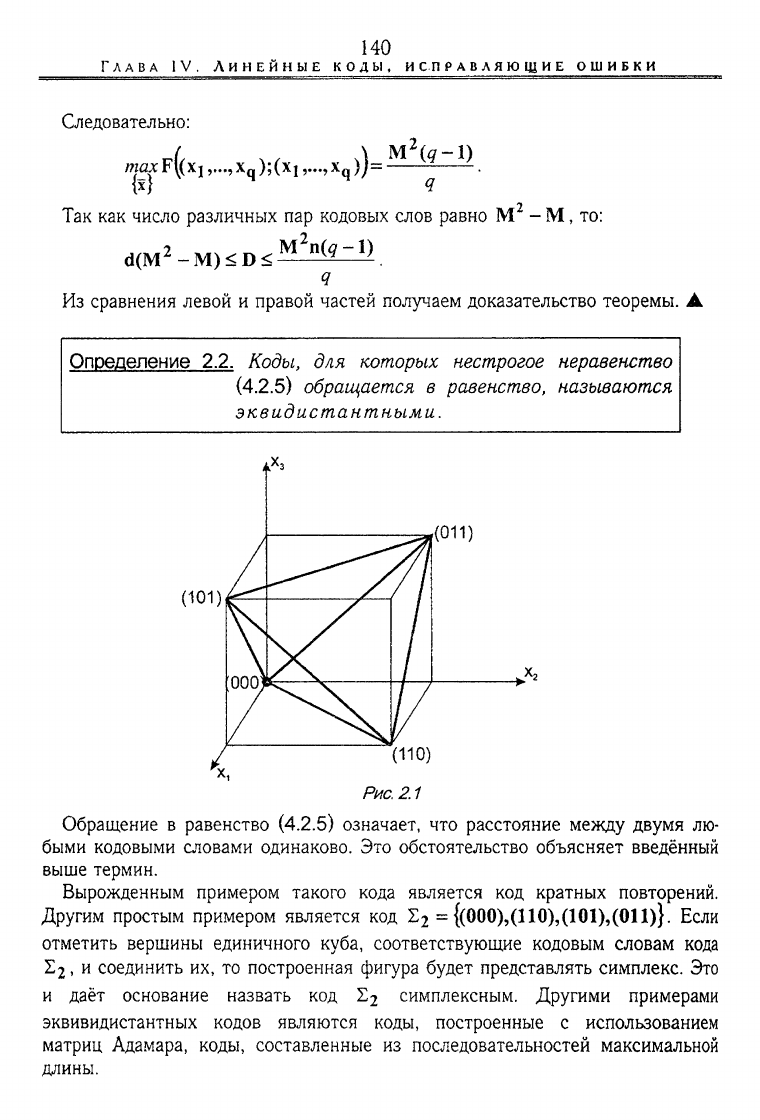
Вырожденным примером такого кода является код кратных повторений.

Другим простым примером является код Z

= {(000)^(110),(101),(011)}. Если

отметить вершины единичного куба, соответствующие кодовым словам кода

соединить их, то построенная фигура будет представлять симплекс. Это

и даёт основание назвать код £

симплексным. Другими примерами

эквивидистантных кодов являются коды, построенные с использованием

матриц Адамара, коды, составленные из последовательностей максимальной

длины.

[(011)

(101)

(110)

Рис.

2.1