Духин А.А. Теория информации

Подождите немного. Документ загружается.

151

Определение

3.4. Вес

смежного класса определим

как вес

мини-

мального

по

весу элемента

данном смежном

классе.

В некоторых случаях

для

линейных кодов

по

полученному вектору

удаётся просто находить минимальный

вес

элемента смежного класса, содер-

жащего

К.

Тогда декодирование можно осуществить

так.

Занумеруем эле-

менты поля

GF(q)

номерами

от 1 до q так,

чтобы нулевой элемент

был

последним:

. .

GF(?)={vi,v

,...,v^«0j.

Пусть получен вектор

h = (х,,...,х

Найдём

вес

смежного класса

+ h.

Затем заменим

на

Найдём веса смежных классов, содержащих полученный вектор

измене-

ной первой компонентой. Пусть

элемент поля, приводящий

макси-

мальному уменьшению веса.

Тогда будем рассматривать

К' = (xj -

,...

сли

уменьшения веса

6 +

не

произошло,

то

будем рассматривать полученный вектор

Проде-

лываем

эту

процедуру последовательно

остальными компонентами.

итоге

будет получен вектор, принадлежащий смежному классу веса

0, то

есть

са-

мому коду G. Предполагается,

что

построенный кодовый вектор передавался

по каналу связи. Предложенная процедура называется последовательным

де-

кодированием.

Приведём

без

доказательства теорему Прейнджа.

Теорема

3.2.

Последовательное декодирование всегда приводит

кодо-

вому вектору. Соответствующий образующий смежного

класса, который равен разности между полученным век-

тором

h и

кодовым вектором, получившимся

резуль-

тате декодирования, имеет минимальный

вес в

своём

классе смежности.

Для реализации метода последовательного декодирования

не

требуется

большого объема памяти.

Рассмотренный здесь основной метод декодирования получает развитие

для

тех

или

иных линейных кодов.

Так,

для

линейного БЧХ-кода

(см. § 8),

исправляющего заданное число

ошибок,

по

полученному вектору определяют синдром, многочлен локаторов

ошибок

и все его

корни, задающие величины искажённых компонент.

§ 3. МЕТОДЫ

ДЕКОДИРОВАНИЯ ЛИНЕЙНЫХ КОДОВ

§4

КОД ХЕММИНГА

Рассмотрим метод построения двоичного кода, исправляющего одну ошибку.

Как следует из § 3, синдром принятого вектора у равен линейной комбина-

ции тех столбцов проверочной матрицы Н, номера которых совпадают с номе-

рами искажённых компонент, а коэффициенты линейной комбинации равны

величинам ошибок. Проверочная матрица Н кода, исправляющего одну ошиб-

ку, должна удовлетворять двум следующим ограничениям. Во-первых, матрица

Н не должна иметь нулевых столбцов. В противном случае ошибка в соот-

ветствующей компоненте не будет влиять на синдром и не будет обнаружена.

Во-вторых, все столбцы матрицы Н должны быть различными. В противном

случае ошибки в соответствующих позициях не будут различаться.

Зададимся числом проверочных символов г = п - к, совпадающим с числом

строк проверочной матрицы Н

Чтобы построить код с максимально возможной скоростью передачи R = ~,

возьмём все допустимые ненулевые двоичные векторы-столбцы из V

(GF(2)).

Для построения матрицы Н

условимся выписывать их в порядке возрас-

тания чисел, двоичные разложения которых совпадают с рассматриваемыми

столбцами. Для г = 3 имеем 2

-1 = 7 допустимых двоичных столбцов, кото-

рые,

согласно договорённости, образуют матрицу Н

следующего вида:

Го о о 1 1 1 Л

0 110 0 11

l 0 1 0 1 0 \j

Используя строение матрицы Н

, покажем индуктивный метод построения

проверочных матриц:

го

1 \\

Го 0 0

1 1

1 0 0 1 1

0 1 0

0 1

0 0 0 1

1 \\

153.

§ 4. Код ХЕММИНГА

0, 0 1

Определение

4.1.

Двоичный код с длиной блока п = 2

-1, прове-

рочной матрицей H

(rxn), образованной всеми

ненулевыми векторами из V

(GF(2)), располо-

женными в порядке возрастания чисел, двоичные

разложения которых совпадают с рассматривае-

мыми столбцами, называется двоичным ко-

дом Хемминга.

Введённый ( п = 2

-1,

к = 2

-1 -г)-код будем обозначать Н

. Рассмот-

рим процедуру декодирования для кодов Хемминга. Пусть произошла ошибка

в i-м символе передаваемого кодового слова g. Подсчитаем синдром полу-

ченного вектора: h = g + , где

(

е. =

0, 0 1 о, о

S(h) = Hh

= H(g + ё^)

= mj = hj.

(

)

Следовательно, если произошла одна ошибка, то синдром S(h) в двоичной

записи указывает номер столбца, в котором произошла ошибка. Соотношение

(4.4.1)

задаёт изящный и очень простой способ декодирования. Из свойств ко-

да исправлять одну ошибку следует, что кодовое расстояние d £ 3. Заметим,

что вектор (1110,...,0) принадлежит Н

, что проверяется умножением на про-

верочную матрицу.

Следовательно, d = 3.

Теорема

4.1.

Код Н

является совершенным.

Доказательство. Так как код Н

исправляет одну ошибку, то множества

D(g) = {£: d(g;g') < 1, g € H

,g' е V

(GF(2))} не пересекаются.

154

ГЛАВА

IV. ЛИНЕЙНЫЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ОШИБКИ

|D(g)|

= n + l = 2

IH,!^

-'.

Число векторов пространства V

, попавших в множества D(g) для

Vg€H

, равно 2

. Это число совпадает с |V

(GF(2))j. Поэтому каждый

вектор длины п находится в одном из таких множеств и, следовательно, код

совершенный. А

Приведём обзор по результатам работ относительно совершенных кодов.

Выше были указаны тривиальный код кратных повторений и код Н

, являю-

щиеся совершенными. Совершенными являются также ^-чные коды, исправ-

ляющие одну ошибку и имеющие длину:

п =

id *2 q - р& (р - простое).

q-l

Это q-чиые коды Хемминга, нелинейные коды Васильева, коды Шенгейма,

двоичный код Голея, исправляющий тройные ошибки и троичный код Голея,

исправляющий двойные ошибки. Известен результат Титвайнена

, заключаю-

щийся в следующем. Если q является степенью простого числа, то не сущест-

вует других q

-чных

совершенных кодов, за исключением перечисленных, ком-

бинаторно эквивалентных им, и тривиальных нелинейных кодов, получающихся

сложением каждого кодового слова указанных выше линейных совершенных

кодов с некоторой фиксированной последовательностью длины п.

Определение4.2.

Двоичным симплексным кодом £

назы-

вают код, двойственный к коду Хемминга Н

По определению двойственного кода порождающая матрица G

кода Н

яв-

ляется проверочной для кода £

, проверочная матрица Н

кода Н

является

порождающей для £

Индуктивный метод построения матрицы Н

позволяет

перечислять все кодовые слова кода Z

Го о о]

1 1

0 1

[1 1 о

A. TetevSinen. "On the

nonexistence

perfect

codes

over

finite

fields".

SIAM

Appt.

Math. 24 (1973),

88-96.

155

§ 4. Код ХЕММИНГА

0 0 0 0 0

0 0'

1 0 0

1 1

1 0 1

0 1 0 1

1 1 0 0 1

1 0

0 0 0 1 1 1 1

1 1

1 0 ! 1 0 1 0

1 1 0 1

0 0 1

Zr-I

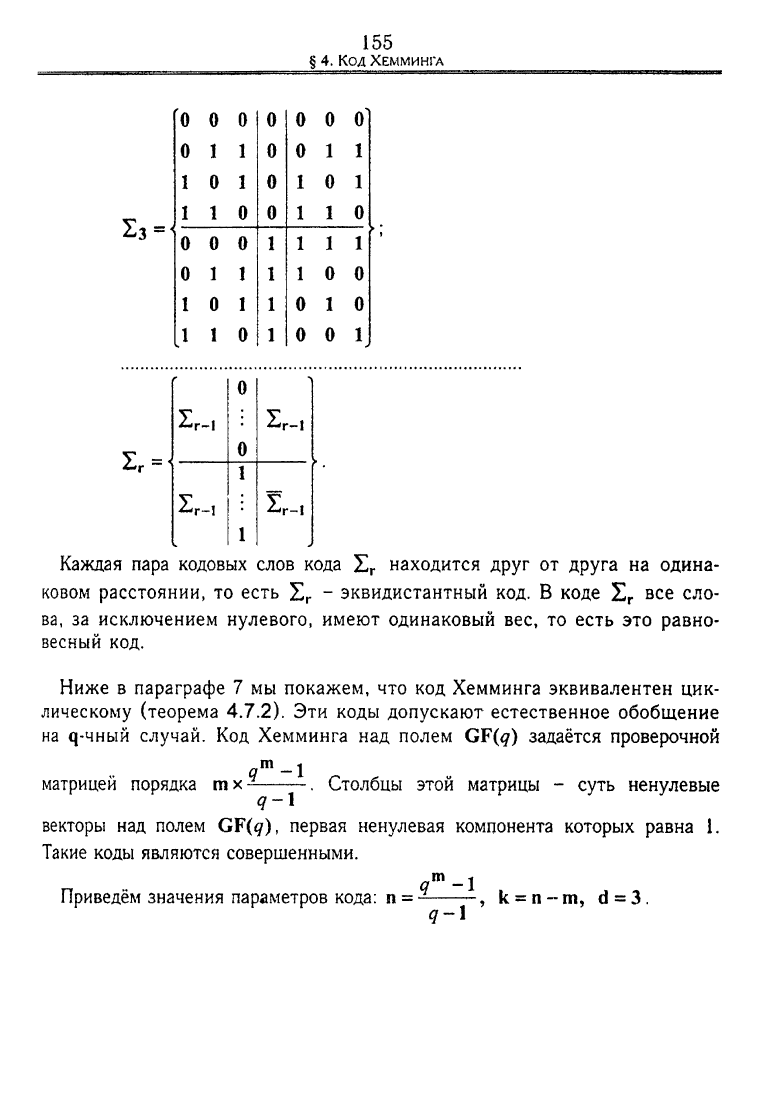
Каждая пара кодовых слов кода Ц

находится друг от друга на одина-

ковом расстоянии, то есть £

- эквидистантный код. В коде £

все сло-

ва, за исключением нулевого, имеют одинаковый вес, то есть это равно-

весный код.

Ниже в параграфе 7 мы покажем, что код Хемминга эквивалентен цик-

лическому (теорема 4.7.2). Эти коды допускают естественное обобщение

на q-чный случай. Код Хемминга над полем GF(q) задаётся проверочной

m _ j

матрицей порядка тх» . Столбцы этой матрицы - суть ненулевые

<7-1

векторы над полем GF(q)

первая ненулевая компонента которых равна 1.

Такие коды являются совершенными.

m _ j

Приведём значения параметров кода: п = , k = n - m, d = 3.

4-1

§5

В этом параграфе будут рассмотрены некоторые методы построения новых

кодов

из

заданных. Предлагаемые методы

ряде случаев позволяют строить

бесконечные серии кодов, коды

большим кодовым расстоянием

или с

большей скоростью передачи.

1°.

Добавление общей проверки

на

четность.

Пусть G

двоичный (п,

к)

код

кодовым расстоянием

d, в

котором

имеются кодовые слова нечётного веса.

Для каждого вектора

g =

(Yiv?Yn)

вычислим

Yn+i^eYi- (4.5.1)

Рассмотрим новый код

{g:(y

,...,Y

n+1

)},

где

Yn+i

опреде-

ляется

(4.5.1).

Если минимальное кодовое расстояние кода

G оп-

ределялось вектором нечётного веса,

то

минимальное кодовое расс-

тояние

кода

будет равно d

+1.

Если код

имеет проверочную

матрицу

((n-k)xn),

то код

G будет иметь следующую провероч-

ную матрицу:

... 1 п

Н = | „ 1 °|.

(4.5.2)

Пример

5.1 (Модифицированный

код

Хемминга). Рассмотрим

код

Хемминга

параметрами

п = 2

-1,

k = 2

-1,

d =

Применяя

этому коду изложенный метод, получим модифи-

цированный код Хемминга

параметрами:

n = 2

, 5 =

Де-

кодирование

для

модифицированного кода Хемминга произво-

дится

по

синдрому

а) Если ошибок при передаче нет,

то s = 0.

б) Если произошла одна ошибка,

то

синдром имеет первую

компоненту

1, а

остальные

компонент задают двоичное

разложение номера искажённой позиции.

МЕТОДЫ ПОСТРОЕНИЯ НОВЫХ КОДОВ

157

§ 5.

МЕТОДЫ

ПОСТРОЕНИЯ НОВЫХ КОДОВ

в) Если произошли две ошибки, то общая проверка на чёт-

ность равна нулю. Некоторые из остальных компонент будут

отличны от нуля - необходима повторная передача.

2°. Выкалывание кодовых координат.

Из всех кодовых векторов одновременно удаляется одна или более

одноименных кодовых координат. Для полученного кода G* при

удалении одной координаты новые параметры будут следующим

образом связаны с параметрами исходного кода

= n-l, k*=k, либо k-1, d*= d, либо d-1.

3°.

Построение кода выбрасыванием слов.

Пусть G содержит векторы чётного и нечётного веса. Слова нечёт-

ного веса образуют класс смежности по множеству векторов чётного

веса. Удалим из G все кодовые векторы нечётного веса. Параметры

нового кода G связаны с параметрами исходного кода так:

n=n, k = k-l, d=d (d>d).

4°.

Пополнение кода путём добавления новых кодовых слов.

Предположим, что вектор ё = (1,..

1) не принадлежит коду

Добавляя к коду G множество G+ё, получаем новый код

со сле-

дующими параметрами:

= n, k

=к + 1, d

= wm{d,n-d'},

где d' - наибольший вес кодовых векторов

5°.

Удлинение кода добавлением информационных символов.

Последовательно из кода

получаем

из

получаем

Параметры построенного кода выражаются через параметры исход-

ного кода следующим образом:

+1, k

= k +1.

6°.

Укорочение кода.

Выбираются все векторы, первая координата которых равна нулю.

Код

составляется из этих векторов после удаления у них первой

координаты:

n' = n-l, k' = k-l, d'>d.

158

ГЛАВА

IV. ЛИНЕЙНЫЕ КОДЫ, ИСПРАВЛЯЮЩИЕ

ОШИБКИ

7°.

Построение кода с помощью прямой суммы.

Параметры кода G следующие:

п = it)

+П2,

k = kj + к

, d = w/«{dj,d

8°. Построение кода с помощью полупрямой суммы.

Лемма 5.1. Кодовое расстояние нового кода выражается формулой:

d = w/w{2d

Доказательство. Пусть а = (uju + v), b = (u'|u' + v') - различные кодовые

слова в G. Если v = v', то

d^b^dCibu'^dj.

Если v*v', то, учитывая неравенство треугольника,

имеем:

d(a,b)=:

= W(u - u') + W(u - u4 v - v') £

W(u - u') + W(v - v') - W(u - u') = W( v - v')

Данная конструкция позволяет строить многочисленные интересные серии

кодов.

Пусть u €G,, veG

, п, = п

n = 2n

Пример 5.2. Рассмотрим в качестве G, двоичный код, составленный из век-

торов чётного веса длины 4, G

- код кратных повторений длины 4 над

GF(2).

Перечислим все векторы кода G:

159

§ 5.

МЕТОДЫ

ПОСТРОЕНИЯ НОВЫХ КОДОВ

0 0 0 0 0 0

1 1

1 1 0 0

1 0 1

1 0

1 0 0 1

0 1

0 1 1 0 0 1 1 0

0 1 0 1 0

0 1

0 1 1 0 0 1 1

1 1 1 1 1

1 1 1 1

1 1 0 0 0 0 1 1

1 0 1 0 0 1 0 1

1 0 0

0 1

0 1 1 0 1 0 0

0 1 0 1 1 0

0 0

1 1 1 0 0

1 1 1 1 0 0 0

Символически список

кодовых векторов можно

записать так:

(

где G] - множество векто-

ров,

сопряжённых коду

Получим код с парамет-

рами:

п = 8,

к = 4,

d = 4.

Рассматривая G в качестве исходного кода

G,,

а в качестве кода

беря код кратных повторений, длины 8, и применяя эту же

конструкцию, получим код с параметрами n=16, к = 5, d = 2

так далее. Полученные коды называются кодами Рида-Малера

первого порядка. Для этих кодов значения параметров следую-

щие:

n = 2

, k = r + l, d = 2

r_1

9°. Произведение кодов.

Пусть G] - систематический (п^к^-код, G

- систематический

(п

,к

)-код. Запишем K = kjk

информационных символов, состав-

ляющих вектор, подлежащий кодированию, в виде матрицы:

А =

*к

к,;

(4.5.3)

Строки матрицы (4.5.3) закодируем кодом

В результате к каж-

дой строке матрицы будет добавлено щ - к

{

проверочных символов,

удовлетворяющих проверочным соотношениям кода

G,:

160

ГЛАВА

IV. ЛИНЕЙНЫЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ОШИБКИ

v>a

lkj

lki+lv-5

tni

(4.5.4)

Далее каждый столбец получившейся матрицы A

Gj t

порядка

xn,, закодируем с помощью линейного систематического

(п

,к

)-кода

4>ixG

,..,,a

1kl

,...,a

lnj

l'"''

9"«?

l'"*'

'"^

ni J

(4.5.5)

Выписывая элементы этой матрицы по строчкам, получим кодовый

вектор, соответствующий исходному информационному вектору.

Проводя эту процедуру для каждого информационного вектора, по-

лучим линейный код

= G

называемый произведением кодов.

Очевидно, что n = n

Лемма

5.2. Минимальное кодовое расстояние кода, построенного по пра-

вилу произведения, выражается формулой: d >

did2.

Доказательство.

Вектор, принадлежащий G и записанный в виде матрицы

(4.5.5),

должен иметь, по крайней мере, dj ненулевых эле-

ментов в каждой строке матрицы

(4.5.5)

и, по крайней ме-

ре,

ненулевых элементов в каждом столбце этой мат-

рицы, если в строке или столбце есть ненулевые элементы.

Следовательно, найдётся вектор, имеющий не менее djd

ненулевых элементов. А

Отметим, что метод получения новых кодов с использованием полупрямой

суммы приведён Плоткиным

M.PIotkirv

Binary codes with specified minimum distances. IEEE Transec. Info. Theory 6 (1960),

pp.

445-450.