Духин А.А. Теория информации

Подождите немного. Документ загружается.

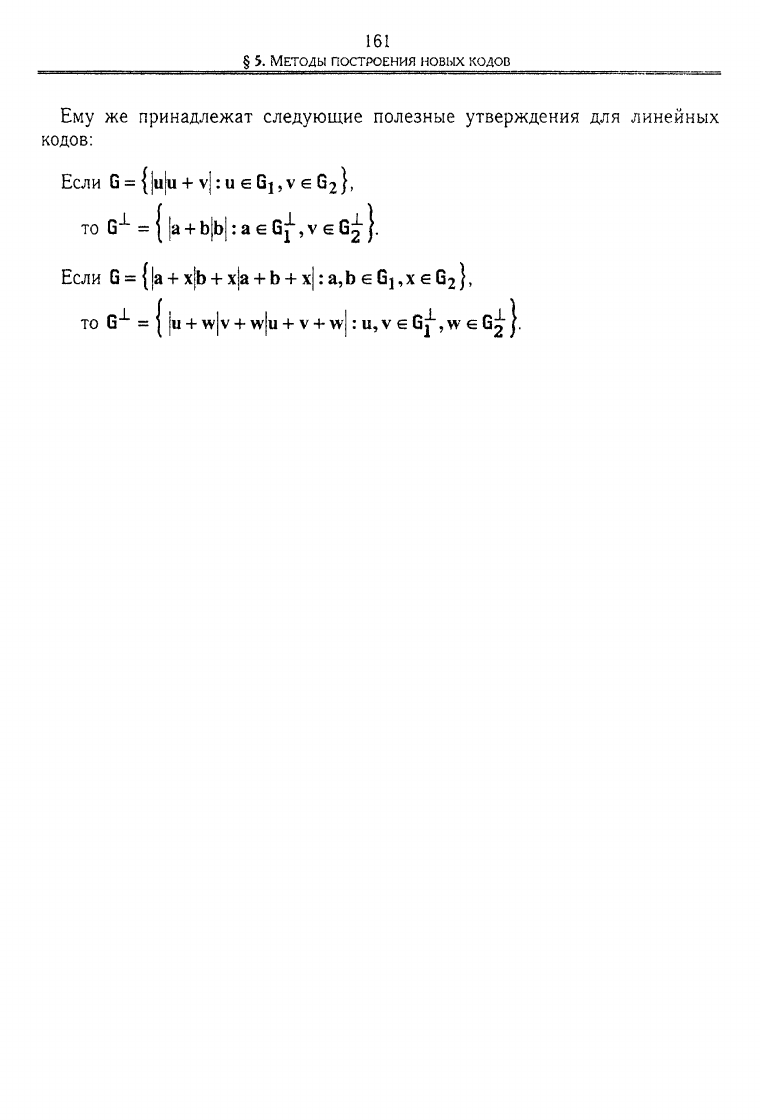
161

§ 5. МЕТОДЫ ПОСТРОЕНИЯ НОВЫХ КОДОВ

Ему же принадлежат следующие полезные утверждения для линейных

кодов:

Если

= {|u|u + v|: u е 6j,

G2},

то G

= {|a + b|b|:aeGjf,veG2 }.

Если G= {|а + x|b + x|a + b + x|:a,b е 6i,x е 62},

то G"

" = j |u + w|v + w|u + v +

w|:u,v€G|",weG2

}•

§6

ТОЖДЕСТВА МАК-УИЛЬЯМС

Рассмотрим (п, к)-код

Обозначим посредством А

{

число таких кодовых

векторов, вес каждого из которых равен i. Числа A

при i =

0,1,...,

п неотрица-

тельные, целые, удовлетворяют соотношениям:

o<Aj<n

2>не|.

Определение 6.1.

Набор (A

..,A

) называется весовым

спектром кода.

Приведём весовые спектры некоторых из рассмотренных выше кодов:

код кратных повторений. А

= А

и А|=0 при i = l,...,n~l;

симплексный код, двойственный к коду Хемминга. Пусть длина кодового

вектора равна n = 2

-1.

Тогда А

= 1, А

_, = 2

-1,

А, = 0 при i * О^"

;

код Рида-Маллера 1-го порядка. Пусть длина кодового вектора равна

n = 2

Тогда А

= А

=1, А

2к

_, =2

-2, А,=0и i

0,2

кЧ

Весовой спектр является важной характеристикой корректирующих

свойств кода. С использованием компонент А

{

могут быть выражены:

вероятность ошибки декодирования, вероятность непринятия решения и т.д.

Нахождение весового спектра связано с подсчётом веса каждого кодового

вектора. При больших мощностях кодов эти задачи могут оказаться трудно

выполнимыми даже для ЭВМ. В некоторых случаях нахождение спектра

кода G можно осуществить, используя известный весовой спектр кода 0

. В

теореме Мак-Уильяме приведены соотношения, позволяющие осуществить

подобный пересчёт.

Приведём без доказательства две леммы, известные из курса алгебры, кото-

рые будут использованы ниже.

163

ТОЖДЕСТВА

МАК-УИЛЬЯМС

Лемма

4.1.

Обозначим U

+ V =

{w;W

= au +

Pv},

где

u е U, v е V, а <х,р -

элементы поля.

Тогда:

dim(U

V) +

dim(l)

+ V) =

dimV

+ dimW.

(4.6,1)

Лемма 4.2. Пусть

ортогональное пространство

для U, V

ортого-

нальное пространство

для V.

Тогда

ПУ

ортогональное

пространство

для

+ V.

Теорема

4.1.

Пусть G

- (п,

к)-код

над

GF(#), G

- (п,

п-к)-код

}

двойст-

венный к G.

{А

,...,А

{В

,...,В

}

- весовые спектры

кодов соответственно. Тогда:

В;Х*

- £ Aj(l -

x)i[l

+ to -

l)x]

(4 6 ?)

i=0

j=0

Доказательство теоремы проведём следующим образом.

В первой части

его

получим

ряд

тождеств, эквивалентных соотношению

(4.6.2).

Во

второй части теоремы докажем справедливость одного

из

тождеств.

Сделаем

ряд

эквивалентных преобразований

соотношением (4.6.2):

ZBjX^^I

I ZAj

i=0

j=0s=0t=0

Чтобы исключить индекс

положим

i = s

+1. Тогда

t = i - s

Заметим,

что

0, когда

s > n, s <

Это

дает возможность расширить

пределы суммирования

внутренних сумм, формально включив

суммы нуле-

вые слагаемые.

. . n j n-j-s

i=0

j=0s=0

i=s

-s

n n

j=0s=0i=0

-s

164

ГЛАВА

IV.

ЛИНЕЙНЫЕ

КОДЫ, ИСПРАВЛЯЮЩИЕ

ОШИБКИ

Изменим порядок суммирования, что возможно для конечных сумм:

-к

Y"-

(-l)*(q-l)

i-s

i=0

i~0 [j=0

s=0v

Приравнивая коэффициенты при одинаковых степенях х, получаем соотно-

шение, эквивалентное (4.6.2):

Bi»r

ZA,E[

Получим третье соотношение. Положим х =

+ у. После подстановки но-

вой переменной у в (4.6.2) имеем:

i В

{

(1 +Y)

= I

AJ(-Y)J[^

+ (

-DYF-J.

I=0

J=0

Сделаем ряд эквивалентных преобразований:

(-l)

(q-l)

(4.6.3)

t \

I=0

M=0V

J=0 K=0V

Чтобы исключить индекс k, положим, что k + j = m. Тогда k = m - j.

n i (i "\ . n n

I=0

M=0

IB,

Y^^IZAJ

J=0m=J

<™-iJ

(-D

-I)

-V~

Расширяя пределы суммирования и изменяя порядок суммирования,

получаем:

n n (i\

ZZB,

=0i=0

M=0 [J=0

m-j

Приравнивая коэффициенты при одинаковых степенях у, получаем:

( i

i=0

N-M-K

IAj

J=0

(-l)Hq

-D

Наконец, полагая x =

+ у) в соотношении (4.6.2), получим:

1в

i=0

(1 +

Y)'

J=0

q-l

l +

n-j

(4.6.4)

Я £

BJ(l

= £

AJY

+ ^r)

J=0

165

ТОЖДЕСТВА

МАК>УИЛЬЯМС

1в,1

'WsVE

i=0 m=0V

/ j=0 k=0V

yk^n-j-k

Чтобы исключить индекс k, положим k + j = m. Тогда получим:

i=0

m=0

(n-i

j=0m=j

-iJ

Расширяя пределы суммирования и изменяя порядок суммирования, полу-

чаем:

« f П-

IB,

m=0

Li=

Замечая, что

вых степенях у, получаем:

n-m-k

IB,

i=0

= 9

n-k-m

приравнивая коэффициенты при одинако-

(4.6.5)

n-m

Перейдём ко второй части теоремы и докажем тождество (4.6.5).

Введём в рассмотрение п-множество N =

(!,2,...,п)

и два его подмножества:

m-множество S = (s

..,s

) и (п-т)-множество T = (t

,.,.

). SUT = N>

Sf)T = 0, l^s

<n, l^tj <n.

Обозначим F

- подпространство, составленное из всех векторов

(GF(g)), компоненты которых с номерами s

,..

могут быть ненуле-

выми, а компоненты с номерами t

..,t

обязательно нулевые. Аналогично,

- подпространство, составленное из всех векторов

(GF(t?)),

компоненты

которых с номерами t,,...,t

могут быть ненулевыми, а компоненты с номе-

рами s

..,s

- обязательно нулевые. Тогда F

- ортогональное пространство

для F

и наоборот.

Введём в рассмотрение пространства Gf|F

По лемме 4.6.2 про-

странством, ортогональным Gf]F

, является G

+ F

(

Обозначим dim(Gf)F

) = d

и dimfi

Г\¥

)

c//w2(G

+ F

) = n-d

, так как (GflFs)

+ F

Из леммы 4.6.1 получаем:

dim (G

+ F

) + dim (G

П F

) = dim G

+ dim F

166

ГЛАВА

IV. ЛИНЕЙНЫЕ КОДЫ, ИСПРАВЛЯЮЩИЕ

ОШИБКИ

Подставляя в это соотношение значения размерностей соответствующих

пространств, получаем:

+ n- k- m. (4.6.6)

Рассмотрим пару, образованную m-множеством S = (s

..,s

) и вектором

eGnF

Если v - произвольный вектор Gf|F

, то в множестве {(S,v) veGflF,.}

содержится q

пар.

Если S меняется произвольно, то общее число таких пар равно:

Пусть вектор

UEG

имеет вес

Среди n-j нулевых компонент выбираем

n - m (m > j). Они определят некоторое (п - т) - множество

T = (t,

..,t

). Задание множества Т однозначно определяет множество S.

Так как множество Т мы можем выбрать

n - m

способами, то в силу

взаимной однозначности таково же будет число множеств S при фиксирован-

ном т.

Следовательно:

IV« - 2 А,

Щ j=o v

n-m

(4.6.7)

Подобным же образом рассматривая G

и множество Т, получаем соотно-

шение

= £

. (4.6.8)

{T}

i=0 V

С учётом (4.6.6) и того обстоятельства, что каждое множество Т опреде-

ляет соответствующее множество S, получаем:

„ у d

+n-k-m d

+n~k-m _ n-k~m

Используя формулы (4.6.7) и (4.6.8), получаем:

п -1

n-k~m

i=0 V

Из последнего соотношения следует:

, п и

n-J

j=0

\n-m

(n-y)

= ZV(i+y)

i=0

j=0

167

§ 6. ТОЖДЕСТВА

МАК-УИЛЬЯМС

Подстановкой у = приходим к соотношению (4.6.2). А

Весовой спектр

(А

..,A

)

и связанная с ним весовая функция

являются мощным средством изучения линейных кодов, таких как: Го-

лея,

Рида-Малера 1-го и 2-го порядков, Кердока, Препараты, кода двой-

ственного БЧХ-коду, исправляющего две ошибки и ряда других. Для при-

ведённых кодов с использованием соответствующих тождеств подсчита-

ны весовые спектры и весовые функции.

§7

ЦИКЛИЧЕСКИЕ КОДЫ

этом

параграфе вводятся в рассмотрение: циклические коды, их порож-

дающая

и проверочная матрицы, будут изучены методы кодирования и декоди-

рования, а также, что наиболее существенно, указан способ задания цикличес-

ких кодов

с помощью специфического порождающего многочлена.

Определение 7.1. Линейный q-чный (п, к)-код G называется цик-

лическим, если вместе с каждым кодовым век-

тором (с

,...,с

) е

коду G принадлежит так-

же и вектор (c

-i?c

,...,c

Для

описания циклических кодов G удобно использовать взаимно-однознач-

ное соответствие векторов кода G и классов вычетов фактор-кольца многочле-

нов R = F[x]/(x

-1), где F[x] - кольцо многочленов над GF(q).

Например, для кода G={ (ООО), (НО), (101), (011) | таким представле-

нием

будет:

[с

(х)Ыо1

[c,(x)]=[l

4 [c

(x)]=[l

J [с

(х)]=[х

Здесь

использованы обозначения: [f(x)J - класс вычетов из фактор-кольца

, содержащий многочлен наименьшей положительной степени f(x).

Отметим,

что умножению на [xj в R

соответствует циклический сдвиг

влево

[x][c(x)I = [x(c

-fc

x +

...

+ c

)] = [c

x + c

+... +

]

= K-i +

i + - +

Сп-г*""

•

Последнее равенство имеет место в силу того, что в фактор-кольце

[х

-1]^[0].

Идеалом

{G| кольца R

называется линейное подкольцо такое, что если

[с(х){€ [G], то |r(x)j[c(x)]€ [G] V[r(x)]eR

. Это условие можно заменить

эквивалентным условием: [G]cR

является идеалом тогда и только тогда,

когда

из jc(x)]e[G] вытекает, что (х][с(х)]е [G].

Определение

7.2.

Циклическим кодом с длиной блока п на-

зывается идеал фактор-кольца R

169

ЦИКЛИЧЕСКИЕ

КОДЫ

Идеал

[G]

с R

называется главным идеалом, если

он

состоит

из

всевоз-

можных произведений элементов

из R

на

некоторый фиксированный много-

член

[g(x)|,

называемый порождающим.

Главный идеал

[G] с

порождающим многочленом

[g(x)j

будем обозначать

(g(x)).

Известно,

что R

является кольцом главных идеалов,

то

есть

любом

ненулевом идеале

[G]

имеется единственный унитарный многочлен

[g(x)]

наименьшей степени, такой,

что

[G]

(g(x)).

При

этом имеет место

g(x)|x

-l.

Действительно, имеет место представление

->l]

[h(x))[g(x))

lr(x)],

где degr{x)<deg%{\).

В кольце

равенство можно переписать следующим образом:

~(r(x)]

= [h(x)][g(x)]€[G].

Это равенство возможно лишь, когда

[г(х)]

= 0.

Если

f(x)

произвольный многочлен, делящийся

на

g(x),

то

[f(x)]e[Gl.

Пусть degg(x)

£. Так как

существует

многочленов степени (п-1)

меньше, которые делятся

на

g(x),

то

число классов вычетов, содержащихся

[G],

равно

~^.

Следовательно,

силу взаимно-однозначного соответствия

между

G и

[G], приходим

выводу,

что deg

g(x)

= I =

- k.

Определение

7.3. Порождающий многочлен

g(x)

= go +

giX

... +

идеала

[G]

называется порождающим многочленом

кода

Рассмотрим

к +

многочленов:

g(x),

xg(x),

~*g(x)

соответст-

вующие

им

векторы, которые представлены

виде матрицы:

(г* Г* ... ГШ Q ... Q^l

G =

О •••

-k

gn-k-I

gn-k

(4.7.1)

Sn-kyj

В силу того,

что

0 и

rang

= к,

матрица

является базисной

для

пространства

G. Это

дает основание рассматривать

порождающей матрицей

кода

170

ГЛАВА

IV.

ЛИНЕЙНЫЕ КОДЫ, ИСПРАВЛЯЮЩИЕ

ОШИБКИ

Определение 7.4.

Многочлен

х"-1

h(x)=

g(x)

(4.7.2)

называется проверочным многочленом

кода

Теорема 7.1.

Двойственный

код G

циклического (п,к)-кода также

яв-

ляется циклическим. Порождающим многочленом кода

является многочлен

h(x""

где h(x) -

провероч-

ный многочлен кода

С, h

свободный член

h(x).

Доказательство.

Пусть

G -

циклический (п,к)-код

порождающим много-

членом g(x)

= g

+ g,x

+...

_kX

проверочным многочленом

h(x)

= h

x +

...

+ h

порождающей матрицей

(4.7.1).

Пусть

(co,.«,c

_j)eG.

По

определению циклического кода

(ci,C2v>Cn-l>

€

Пусть

(dov.^dn.^e

Тогда Cjd

C2CIJ

+...-нс

0. Последнее

ра-

венство можно переписать

следующем виде:

Cpd^t

+ с^

+...

=0,

означающее,

что (ci

..,d

)е G

Следовательно,

циклический

код.

Обозначим порождающий многочлен кода

посредством g

(x). Введём

вектор:

(hk>

k-iv--,h

,0,...,0).

n-k-l

Тогда:

k k-1

= (1]ь

|8|

;ХЬк^^;».;ь^о) =

(0,...,0)

i=0

Последнее равенство имеет место

силу g(x)h(x)

~ х

-1.

Так как

введён-

ный вектор

ортогонален

G, то h е G

Рассмотрим унитарный многочлен

h(x~

)

...

elG

Поскольку

главный идеал размерности

к, то

многочлен

h(x~

)

дол-

жен делиться

на

порождающий многочлен g

(x).

Заметим,

что

degg

(x)=deghQ

h(x~

)

= k и оба

многочлена унитарные.