Духин А.А. Теория информации
Подождите немного. Документ загружается.


231
ЗАДАЧИ
5.
Подсчитать пропускную способность п одинаковых ДСК, сое-
диненных последовательно.
6. Пусть п одинаковых ДКБП
[А,В;Р]
соединены последова-
тельно. Покажите, что матрицы переходных вероятностей Р
результирующего канала
[А,В;Р]
представлены в виде Р = Р
П
.
7.
Пусть п одинаковых симметричных ДКБП соединены последовательно.
Используя результат предыдущей задачи, покажите, что
результирующий канал будет симметричным.
8. По ДСК передаются слова двоичного равновесного кода
G
= {g:W(g) = k}, где k<^> с равномерным распределением на
множестве кодовых слов.
Докажите, что р(ар = 1)= —, где ар* - i -я (i =
1,...,п)
компонента j -го кодового слова.
Обозначим р = —.
п
Cj=pfcgp + (l-p)fog(l-p)-
- [(р(1
- Р) +
(1"
P)P>*g(p(l ~ Р) ~
(1"
Р)р)+ (q -
Р(1
~ 2p)>og(q -
р(1
- 2р))1
Докажите, что
—
1(В;С) < С
0
, где В =
п
р
I
UJ J
,
VgeG;
С
- вероятностная схема на выходе ДСК.
9. Пусть для вероятностного распределения Р(А) случайная величина
I(a;b) (а€А,ЬеВ), А и В входной и выходной алфавиты ДКБП
[А,В;Р] имеет нулевую дисперсию.
Докажите, что на этом распределении р(А) реализуется
пропускная способность канала.

232
ГЛАВА
V. ДИСКРЕТНЫЕ КАНАЛЫ ПЕРЕДАЧИ
ИНФОРМАЦИИ
10.
Буквы, порожденные источником
[A,iKs)]=[(ai,a
2
,a
3
), р(а,) = р(а
2
) = 1/4, р(а
3
) = 1/2],
передаются одновременно по двум каналам:
Ь, а,
1
с,
Ь
2
а
2 ^^^^^
02
а
3
-^^
'
2
а-г"""""""^
Вычислить: Н(А), Н(В), Н(С), Н(ВС), 1(А;В); 1(А;С).
11.
а) Для ДКБП показать, что энтропия Н(В) для символов на вы-
ходе канала является выпуклой вверх функцией от входного
распределения. Рассмотреть случай, когда функция Н(В) яв-
ляется не строго выпуклой.
Ь) Показать, что средняя взаимная информация между входной
и выходной вероятностными схемами является выпуклой
функцией относительно входного распределения.
12.
Рассматриваются три канала:
. ДСК,
. двоичный канал со стиранием,
. канал, задаваемый представленной диаграммой:
1-РгР*
a)
ДЛЯ каждого из каналов вычислить функцию:
Р
е
=
Ур(ь/«0'~
к
Р(ь/1)
к
.
b€V
n
(GF(2))
b) Найти минимум функции Р
€
(к) по ke[o,l].
c) Найти верхнюю границу вероятности ошибочного декодиро-
вания по методу максимума правдоподобия при использова-
нии кода кратных повторений.

233
ЗАДАЧИ
d) Получить асимптотическое представление этих вероятнос-
тей, применяя формулу Стирлинеа:
[Qfi
0,1 0,05
0,05У
кодируются двоичным кодом:
G
= -(00000),а
2
-(01111),а
3
-(10101),а
4
-(11010)},
и передаются по ДСК.
Необходимо:
а)Построить множество
(Щ)
= {g: W(g- Ij) £
1, g G
V
5
}.
b)
Построить функцию
Р
е
0ч)
i
=1,2,3,4.
c) Подсчитайте вероятность ошибки передачи по ДСК.
14.
Пусть двоичный код
G^fgj,...,^;^ G
V
n
} используется для передачи
по ДСК с вероятностью ошибки р.
Показать, что
Р
е
(т)*
^
е
кёт,Ёт
/
>«Л/4р(1-р)] <(
М
_
1
)
е
^
Л
/4р(1~р)
где Р
с
(т) - вероятность ошибки при условии, что на вход кана-
ла поступило кодовое слово g
m
;
d - кодовое расстояние.
15.
ДКБП
[А,В;Р]
называется аддитивным по модулю к, если его входным
и выходным алфавитами является множество символов
{o,l,...,k~l}
и
вход А связан с выходом В и шумом С посредством равенства
Ь = аФс, где аеА,ЬеВ,сеС и Ф - операция сложения по модулю
к.
Вход и шум статистически независимы.
13.
Исходы a
f
вероятностной схемы А
Необходимо:
а) доказать, что
1(А; В)
~ Н(В) - Н(С);

234
ГЛАВА
V. ДИСКРЕТНЫЕ КАНАЛЫ ПЕРЕДАЧИ
ИНФОРМАЦИИ
b) выразить пропускную способность С рассматриваемого ка-
нала через энтропию шума Н(С);
C)
найти входное распределение, на котором достигается про-
пускная способность С*.
/у
_0_
16.
Используя формулу Стирлинга
n!~V2rcn
— е
12п
,
0<@<1,
по-
\*)
кажите справедливость энтропийных оценок для биномиаль-
ных коэффициентов:
а)
\ »
е
пН(
Р)
й
(A
S
J
N
е
пн(р)
V
»k(n
- к) [к) ^2т1к(п-к)
где Н(р) = -р/лр -
(1
- р) ln(\ - р); р = —.
п
b)
JJe""W^f
n
Se
nH(p)

ПРИЛОЖЕНИЕ

ПРИЛОЖЕНИЕ
1°.
Докажем справедливость неравенства:
x-l£/wx, х>0. (П.1)
Доказательство.
Нетрудно видеть, что:
lim (х -1
-
/л х) ~ lim (х -1
-
1пх)
= +оо.
х-»0+
х->+со
Функция f(x) = x-l-/«x имеет единственную стационарную точку
х = 1, что следует из уравнения f
f
(x) = 1-- = 0.
х
Значение функции f (х) в стационарной точке, являющейся точкой мини-
мума, равно нулю.
Следовательно, для всех х>0
ХФ\
функция f(x)>0. При
х-1 х ~
1
= /пх. А
2°.
Докажем неравенство Иенсена для выпуклых функций.
Определение.
Непрерывная на [а,Ь] функция f(x) называется
выпуклой, если для любых точек x
l5
x
2
efa,b] и
любых q
x
,q
2
qi £ 0,q
2
£О, q
t
+ q
2
=
1
выпол-
няется неравенство:
qif(x
l
)
+
q
2
f(x
2
)£f(q
l
x
1
+q
2
x
2
).
(П.2)
Выпуклая на }а,Ь] функция f(x) удовлетворяет неравенству:
4if(xi)+q
2
f(х
2
)+•••+q
n
f(х
п
) *
f(4iXi+q
2
x
2
+»•+q
n
x„).
(П.З)
n
где q
f
£ 0 i =
l,...,n
^Tq
f
= 1.
Доказательство.
Докажем неравенство Иенсена индукцией по п. Для
п
= 2 получаем определение выпуклой функции. Пусть справедливо нера-
венство (П.З). Докажем, что оно верно для n +1:
q*f (*i)+q:f (х
2
)+«•+q
n
f (х„)+q„+if
(*
n+
,)
^
<;f(q,x, +
...
+ q
n
x
n
+ q
n+1
x
n+1
),
(П
.4)
q,£0 isl,,..,n + l, Zqj =1.

237
ПРИЛОЖЕНИЕ
Представим сумму двух последних слагаемых в следующем виде:
qnXn+qn
+
ix„
+
i
=
(q„+q„
+
i)
—~—
x
n ^
Un+qn+i
q
n
+
q
n
+i
Тогда правая часть неравенства (П.4) принимает вид:
F(Q
1
X,+.-.
+
Q
B
X
B
+Q
N+1
X
B+
,)
=
=
F
QIXI+-+(Q
n
+4n+H
q
n
Xn
+_q«±L_
X
,qn
+
q
n+
i
q
n
+
q
n+
i
Применяя индуктивное предположение, получаем:
qn
,
q*i+i
n+l
n-1
Л1+1
С учётом определения выпуклой функции (П.2) левая часть последнего не-
равенства может быть преобразована:
£q,f(x,)+(q
B
+q..+i) 21
f
(*n)+(q„
+q„
+
i)-^
±l
~fx„
+1
*
i=i q
n
+q
n+
i q„+q
n+
i
что доказывает справедливость (П.З) для n е N. А
3°.
Пусть f(x) - гладкая выпуклая функция и
Е|£|<+ОО.
Тогда:
F(EO>E
V
F®.
(П.5)
Если, в частности,
F
(х) = х, 0 < v ^ 1, то
(Е£,)
У
*Е$\ (П.6)
Доказательство.
Из определения выпуклой функции получаем, что:
F(x)<F(x
0
)
+ k(x
0
)(x-x
0
). (П.7)
Неравенство (П.7) геометрически означает, что график выпуклой гладкой
функции F(x) лежит под графиком прямой, проходящей через точку
(x
0
,f(x
0
)),
k(x
0
) - угловой коэффициент касательной, проходящей через
точку х
0
. Положим в (П.7), что х = х
0
=
Е£,
тогда:
F(§)IF(E§)
+
(6-E©K(E5).
Найдём математическое ожидание от обеих частей неравенства:
EF
ft) <
F
(Е5) + (Е$- E$)k(ES) =
F (В©.

238
ПРИЛОЖЕНИЕ
Полагая f(x) = x
v
, получаем:
4°.
Получим энтропийную оценку для биномиальных коэффициентов:
£2 ^
га
А)
где H(^M
=
-^Iog^-^bg^.
\щ m
J
m mm ш
(П.8)
Доказательство.
Проведём индукцию по т. Покажем, что для любого
meN
справедливо:
m
га
(П.9)
При m =
1
неравенство (П.9) обращается в равенство. Пусть (П.9) справед-
ливо для т~1. Докажем его справедливость для ш. Рассмотрим отно-
шение:
чШ-1
y
2
-l •
( i\
При этом считаем, что £
2
> 0. Так как
1
+
—
- возрастающая последова-
тельность, то в силу того, что (m
-1)
2 ^
2
-1,
получаем:
Перепишем это неравенство в следующем виде:
(т-1Г
m
У
2
) fm-1
m
ш
\*1
(П.10)

239
ПРИЛОЖЕНИЕ
Последнее неравенство справедливо в силу индуктивного предположения.
Рассмотрим двоичный логарифм левой части неравенства
(П.10):
log
2
m
ft ft
••
-fy\lagt\
-iilogm]-[i
2
lo
g
e
2
-e
2
logm]
=
•t
l
log^-t
2
log^-
= m
m
m
m m m m
= mH
\m
mJ
Подставляя это представление в
(П.10),
получаем доказательство энтропий-
ной оценки
(П.8).
А
5°.
Докажем справедливость неравенства:
i=l
i=l
n
n
(П.11)
1=1
i=l
Доказательство.
Для доказательства воспользуемся неравенством;
/их 1 Л 1}
logx = — £ — 1— .
/«а
In
а
^
х)
Если х £ 1, то ~ > - при
1
< t < х и
t X
(П.12)
InX = I— >- Jdt =
-(x-l)
= l--.
Г t x * x x
Если
0^х<1,
то -->-— при х< t<1
t X
/«X
=
-£,-1 J
dt =
_I
(1
_
x)=1
_i.
J
t X
J
X X
Следовательно, неравенство
(П.12)
справедливо для любого х£0.
Рассмотрим вещественные числа
п
п
{р«Мч»}
«=
1,...
э
п
р^0,
Ч|
>0
2Р,=^=1.
i=l
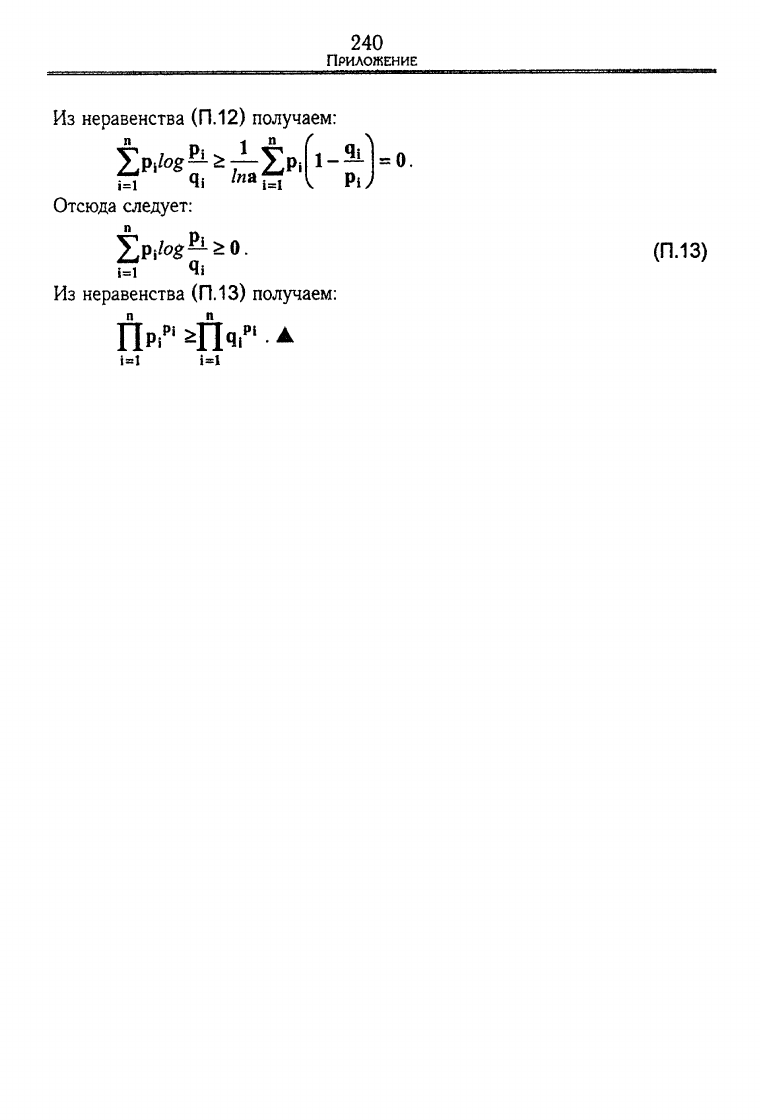
240
ПРИЛОЖЕНИЕ
Из неравенства
(П.12)
получаем:
Р<^РНУ°-
Отсюда следует:
£
Pi
/e>£^>0.
(П.13)
Из неравенства
(П.13)
получаем:
ftp,"
^ПЧ,"'
А
1=1 i*l
