Духин А.А. Теория информации
Подождите немного. Документ загружается.


221
§
4.
ТЕОРЕМЫ
КОДИРОВАНИЯ
ДЛЯ
ДИСКРЕТНЫХ
КАНАЛОВ
БЕЗ
ПАМЯТИ
для v е
[ОД]
в силу неравенства Иенсена для выпуклых функций
3
. Следова-
тельно, рассматривая параметр v е
[0Д1,
получаем:
V
1
EP
m
(e)<; lEp(c/b
m
)l+v
fa}
1
£Ep(c/b
m
<)
1+v
т'
(5.4.9)
На множестве входных слов задано вероятностное распределение
W(B
n
).
Следовательно:
j
j_ JL
Ep(c/b
m
)^v
=
^
W
(b
m
)p(c/b
m
)^v
=
У W(b
m
.)p(c/b
ra
0
,+v
,
где в последней сумме заменён индекс суммирования m -> m'.
Подставляя это выражение в формулу
(5.4.9),
получим:
_
v
1
EP
m
(e)£ YEp(c/b
m
)l+v
1
I IW(b
m
')p(c/b
ra
0
1+v
= (M-1)
V
У £W(b)p(c/b)
1+v
{в„}
(5.4.10)
Полученная формула дает возможность оценить вероятность ошибки де-
кодирования для произвольного канала без каких-либо уточняющих предпо-
ложений.
3°.
Рассмотрим ДКБП. Пусть на вход канала последовательности Ье{В
п
}
поступают покомпонентно. На выходе они также появляются покомпонент-
но.
В силу предположения о канале получаем:
P(=/b)=flp(y
jf
/b
k<
).
<
5
-
4
-
11
)
Предположим далее, что символы кодовых слов, поступающих на вход
канала, подаются независимо, согласно входному распределению на
алфавите входа. Если
{b
l5
...,b
r
}
- входной алфавит, то для Ье{В
п
}
выполняется:
3
СМ.
Приложение,
П.2, П.3.

222
ГЛАВА
V. ДИСКРЕТНЫЕ КАНАЛЫ ПЕРЕДАЧИ
ИНФОРМАЦИИ
W(b)
=
no>
k
^
(5.4.12)
Подставим выражения (5.4.11) и (5.4.12) в формулу (5.4.10):
S Йок/РСг^/ЬкР^
Сумму произведений представим в виде произведения сумм:
. -|l+v
EP
m
(e)£(M-l)
v
У j
t
c
n}
ЕР
т
(е)^(М-1)
У
П^
E«>k,p(VM
1+v
= (М-1Г
z
Z^kPkj
1+v
k=l
1+v
Z<»kPkj
i_V
+v
1+v
k=l
Для скорости передачи информации R введём представление R =
(5.4.13)
InM
Следовательно, при заданном R имеет место представление M=e
nR
. Так
как при заданных n,R величина e
nR
не будет целой, то. под кодом длины
п со скоростью передачи R понимают код с ] e
nR
[ кодовыми словами
длины п. С учётом этого перепишем оценку (5.4.13):
J_V
+v
"
1+v
Z^kPkj
EP
m
(e)<exp -n
-vR-ln]T
k=l
(5.4.14)
Так как правая часть оценки (5.4.14) не зависит от т, то, усредняя по
всему множеству {В
п
}, получаем:
\l+v"
Р(ё) < ехр
-vR-lnJ
1
1+v
k=l
(5.4.15)
Используя естественные соображения относительно среднего Р(е) по ан-
самблю кодов и вероятности ошибки передачи для одного кода, получаем
доказательство теоремы. А
223
§
4.
ТЕОРЕМЫ
КОДИРОВАНИЯ
ДЛЯ
ДИСКРЕТНЫХ
КАНАЛОВ
БЕЗ
ПАМЯТИ
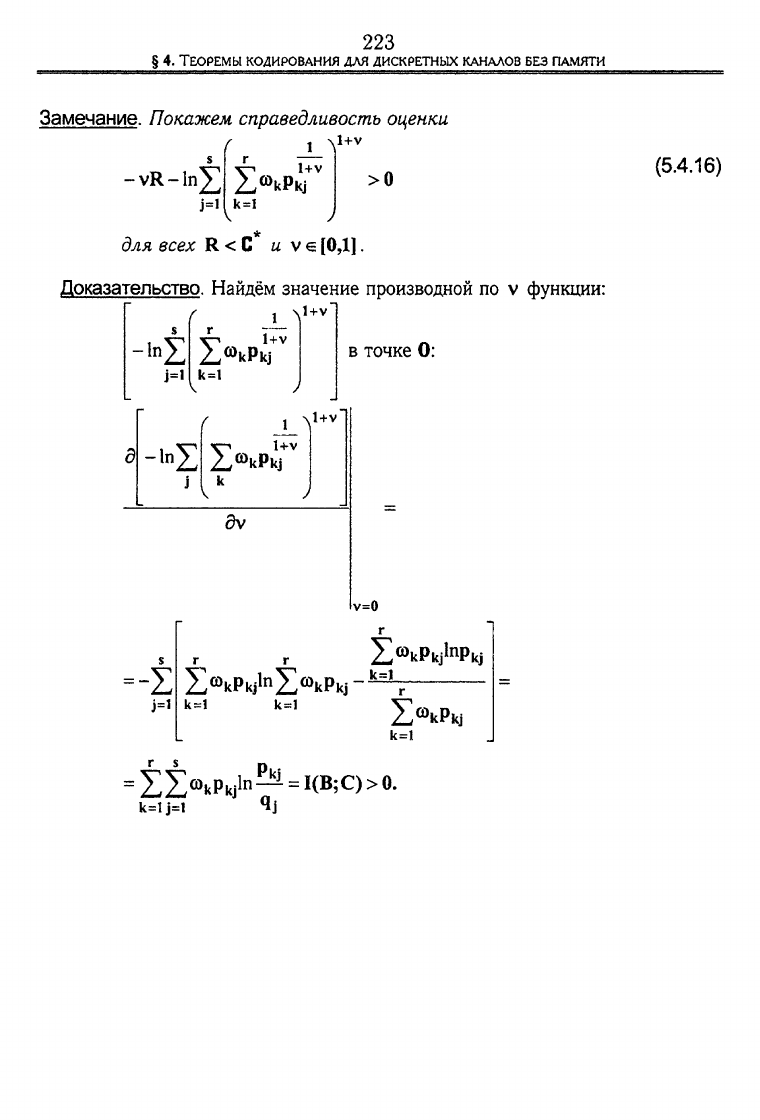
Замечание.
Покажем справедливость оценки
•vR-LNJ]
j=i
i_V
+v
1+v
k=I
>0
(5.4.16)
для всех
R <
С
и v
€
[0,1].
Доказательство.
Найдём значение производной
no v
функции:
1+v"
S
j=1
\-»
1+V
Z^kPkj
k=1
V.
•
в точке
0:
Z
l+V
<*>kPkj
k
av
v=0
E<OkPkj»nPkj
E^kPkj^Z^kPkj -*=H
Ё^кРц
k=l
k=1
= ZZ
<
°KPkj
ln
— =
«B;C)>0.
k=lj=!
4j
224
ГЛАВА
V. ДИСКРЕТНЫЕ КАНАЛЫ
ПЕРЕДАЧИ
ИНФОРМАЦИИ
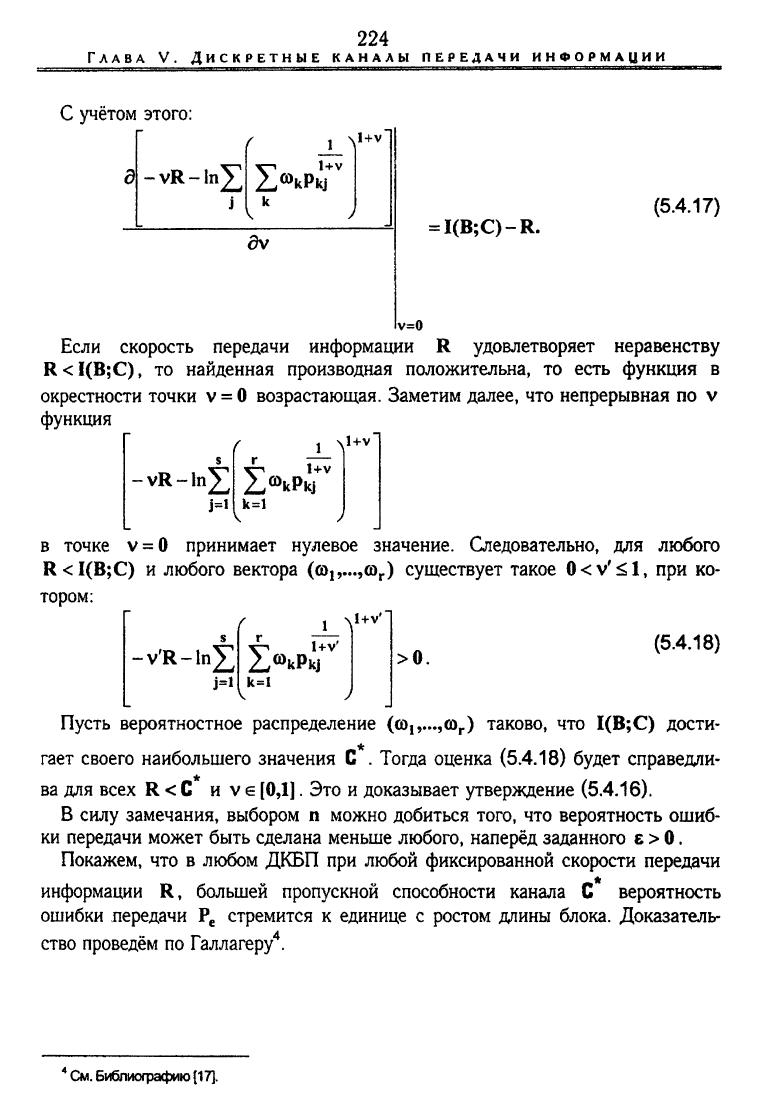
С учётом этого:
-vR-In]T
L
y+v
1+v
dv
= I(B;C)-R.
(5.4.17)
v=0
Если скорость передачи информации R удовлетворяет неравенству
R<I(B;C), то найденная производная положительна, то есть функция в
окрестности точки v = 0 возрастающая. Заметим далее, что непрерывная по v
функция
г 1 V
+v
"
-vR-ln£
чг-ч 1+v
k=l
в точке v = 0 принимает нулевое значение. Следовательно, для любого
R<I(B;C) и любого вектора
(щ,...,ф
г
)
существует такое
0<v'^l,
при ко-
тором:
1+v'
/R-ln£
I>kPkj
+
k=l
>0.
(5.4.18)
Пусть вероятностное распределение (<Di,...,<D
r
) таково, что
1(В;С)
дости-
гает своего наибольшего значения С*. Тогда оценка (5.4.18) будет справедли-
ва для всех R <
С*
и v е
[ОД].
Это и доказывает утверждение (5.4.16).
В силу замечания, выбором п можно добиться того, что вероятность ошиб-
ки передачи может быть сделана меньше любого, наперёд заданного г > 0.
Покажем, что в любом ДКБП при любой фиксированной скорости передачи
информации R, большей пропускной способности канала С* вероятность
ошибки передачи Р
е
стремится к единице с ростом длины блока. Доказатель-
ство проведём по Галлагеру
4
.
4
См. Библиографию [17].

225
§ 4.
ТЕОРЕМЫ КОДИРОВАНИЯ
ЛАЯ
ДИСКРЕТНЫХ
КАНАЛОВ
БЕЗ
ПАМЯТИ
Теорема
4.2
(Обратная теорема кодирования Вольфовиш).
В
произвольном
ДКБП [В;С;Р]
с
пропускной способностью С*
>0 для лю-
бого кода
с
длиной кодового блока
п и
скоростью передачи
R
>
С* вероятность ошибки передачи ограничена снизу:
n(R-C*)
n(R-C У
где
А -
конечная положительная постоянная, зависящая
от канала
и не
зависящая
от п и R.
Доказательство. Обозначим через
<&
1V
..,<D
R
-
входные вероятности,
на ко-
торых реализуется пропускная способность канала:
г
Предположим,
что
канал удовлетворяет ограничениям:
Р(с/Ь)
=
Пр(у
к
/Ь
к
),
4(c)
=
flq
jk
k=l
k=H
Как следует
из
теоремы 5.2.2:
о<кв;с)= £
p^inP-B-sc*,
k=w.
(5420)
Будем измерять энтропию
и
информацию
в
натуральных единицах:
I(B;C)^ln^^ = |;i(b
k
;Y
k
),
(5А2
1)
где I(b
k
;y
k
) = ln
^
k
а
величина
1(В;С)
представляется
в
виде суммы
Чк
независимых, одинаково распределенных случайных величин I(b
k
;y
k
).
Рассмотрим код
с
длиной блока
п и
числом кодовых слов
М.
Декодирование осуществляется
по
методу максимума правдоподобия, путём
разбиения
{С
п
} на
непересекающиеся области С^.^С^
1
:
м
Uc?=c.
t
с?пс? =0.
Вероятность правильного декодирования для рассматриваемого кода равна:
1
м
р
с=^1 Е^/Ь.).
(5.4.22)

226
ГЛАВА
У. ДИСКРЕТНЫЕ КАНАЛЫ
ПЕРЕДАЧИ
ИНФОРМАЦИИ
Зададимся величиной е > 0 и для каждого m =
1,...,М
введём области:
ЧГ
e
js:
I(b
m
;c)
> n(C* + в)}. (5.4.23)
Наряду с DJJ
1
введём их дополнения D^
1
=C
n
\D™. Перепишем выраже-
ние (5.4.22) в следующем виде:
I
м
_
1
м _
р
с=^1 I
P(c/b
m)
+
-£ I
P(c/b
m
).
(5.4.24)
Для векторов с е
D™
из формулы (5.4.23) получим:
P(c/b
ro
)<q(c)e
0(C%e)
.
Оценим вторую сумму в формуле (5.4.24):
1 М 1 м
^ I Z *&Ъ
т
)*± I I q(c/b
m
)^ (5А25)
.п(С*+е)
м
р
п(С*+е)
М
m=l
5eC
m
М
При последнем переходе использовали дизъюнктивное представление
м
(Jc™ =С
П
и тот факт, что
(q(c)}
есть вероятностное распределение на С
п
.
m=1
Для оценки сверху первой суммы в формуле (5.4.24) расширим область
суммирования с СЦ
1
ПОЦ
1
до DJJ
1
:
£
Р(
с/ь
и
)<
JP(c/b
m
)
=
P(l(b
m
;c)>n(C*
+е)/b
m
).
(5.426)
CECFFLDG
1
CED?
В последней оценке использовано, что
I(b
m
;c)
- случайная величина,
принимающая свои значения с вероятностями
P(c/b
m
),
при заданном
b
m
. Аналогично формуле (5.4.21)
I(b
m
;c)
- есть сумма п независимых,
одинаково распределённых случайных величин, у каждой из которых ма-
тематическое ожидание ограничено величиной пропускной способности -
С*.
Используем неравенство Чебышева:
М
, _ v ZDI(b
(
m
>
;Yk)/bS
)
£p(c/b
m
) = p(l(b
m
;c)-nC*
>о*/Ъ
т
)&*&
, (5.4.27)
C6D|P
n £

227
§
4.
ТЕОРЕМЫ
КОДИРОВАНИЯ
для ДИСКРЕТНЫХ
КАНАЛОВ
БЕЗ ПАМЯТИ
где дисперсия случайной величины вычисляется
по
формуле:
м(ь(
т
к)
;у
к
)/Ь^=^
Р
(
У]
/Ь<
т
к
>)
ln-
4j
qj
Так
как Ь^еВ, то
01(ь^
}
;у
к
)
всегда ограничена сверху конечным чис-
лом
А:
A^maxDI^yJ,
к
'
то оценка (5.4.27) принимает следующий
вид:
^
" 4Е
2
С учётом формул
(5.4.25) и (5.4.28)
вероятность правильного декоди-
рования оценивается сверху следующим образом:
А
е
п(С
*
+е)
Л
М
(5.4.28)
пе
Полагая
М = e
nR
, е =
R-C
получим:
Р„
21-
4А
n(R-e)
n(R-C
у
—е
(5.4.29)
что
и
доказывает теорему.
•
Из последнего неравенства видно, что при п
-» да Р
е
->
1.

ЗАДАЧИ
На вход ДСК поступает случайная двоичная последовательность с неза-
висимыми равновероятностными символами.
Найти математическое ожидание взаимной собственной ин-
формации между последовательностью п букв на входе и вы-
ходе канала.
2.
Задан двоичный канал со стиранием
[А,В;Р],
где А = (0,1), В = (0,1,е),
_(61/64 1/64 1/32^
~[l/64 61/64 1/32/
Буквы входного алфавита поступают равновероятно и при этом входные
символы, так же как и выходные, статистически независимы между со-
бой, соответственно.
Требуется подсчитать:
a) взаимную информацию I(a
£
;pj) i = 1,2; j = 1,2,3;
b) математическое ожидание и дисперсию взаимной информа-
ции
I(ot
l
;P
j
).
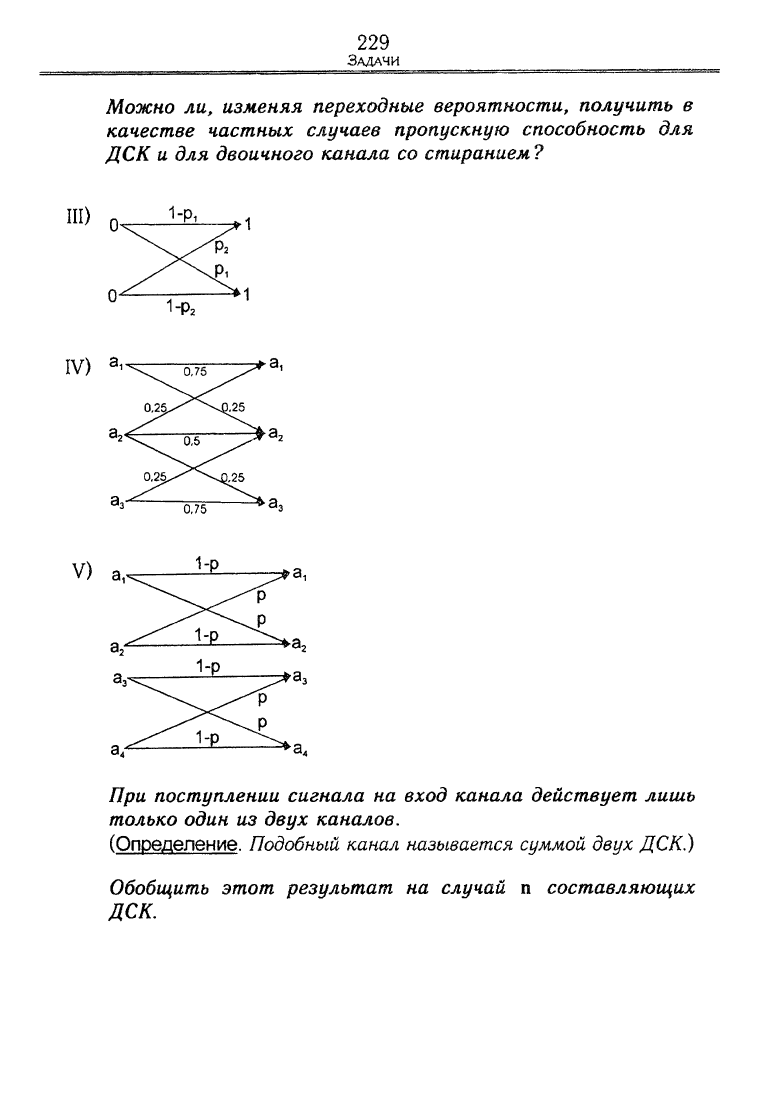
3.
а) Найти пропускную способность С* следующих каналов.
Ь)
Указать то входное вероятностное распределение, на кото-
ром реализуется пропускная способность С*.
229
ЗАДАЧИ
Можно ли, изменяя переходные вероятности, получить в
качестве частных случаев пропускную способность для
ДСК и для двоичного канала со стиранием ?
а,
а
3
а.
^р
\р
1-р
^1 р
^Р
а
1
Яра
поступлении сигнала на
только один из двух каналов.
(Определение.
Подобный канал
Обобщить этот результат
ДСК.
вход канала действует лишь
называется суммой двух ДСК.)
на случай п составляющих
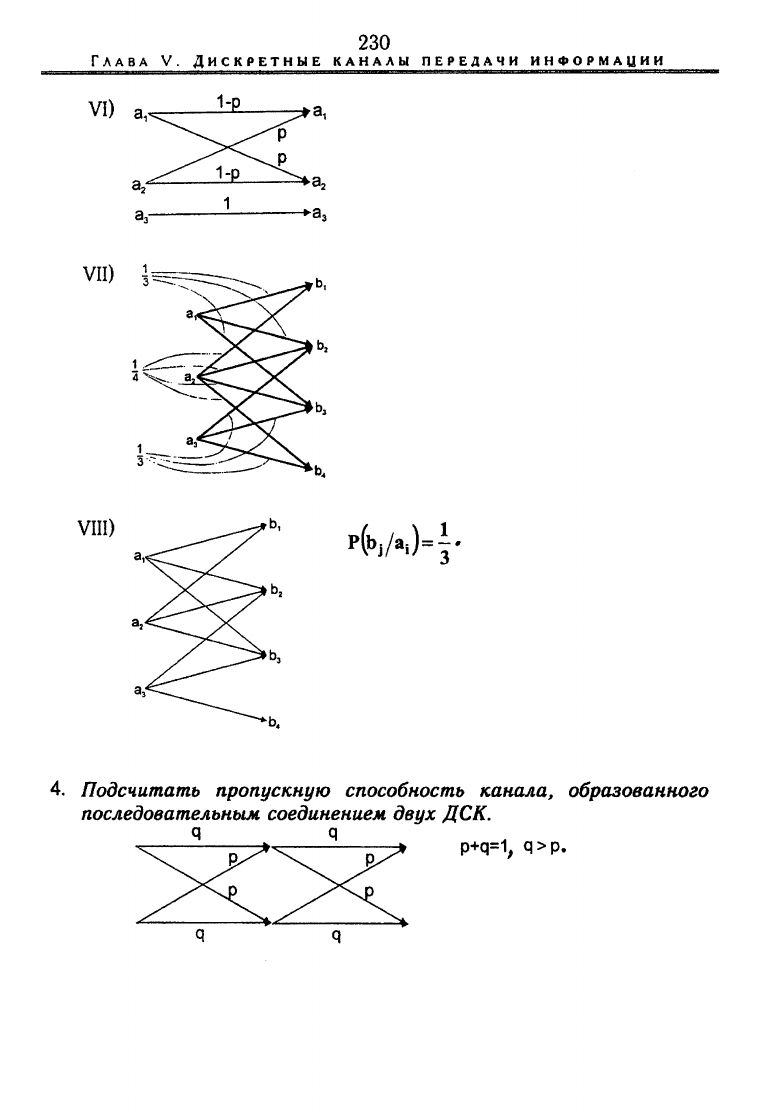
4.
Подсчитать пропускную способность канала, образованного
последовательным соединением двух ДСК.
p+q=1, q>P.
q
