Духин А.А. Теория информации

Подождите немного. Документ загружается.

141

§ 2. ГРАНИЦЫ ДЛЯ ПАРАМЕТРОВ КОДОВ

Перейдём к рассмотрению нижней границы для скорости передачи инфор-

мации. В следствии леммы 4.1.3 было доказано следующее положение:

Блоковый код, являющийся ортогональным пространством матрицы Н,

имеет минимальный вес, равный, самое меньшее, d, тогда и только тогда, ког-

да любая совокупность d-1 столбцов матрицы Н является линейно незави-

симой.

Используем этот результат для построения кода с г проверочными симво-

лами и минимальным весом d.

Теорема 2.3 (Нижняя граница Варшамова-Гилберта). Существует

(n,k)-

код с кодовым расстоянием, равным, по меньшей мере, А,

параметры которого удовлетворяют неравенству:

i=0

(q-l)

. (4.2.13)

Доказательство. Как следует из сделанного выше замечания, построение

матрицы Н, любые d-1 столбцов которой линейно независимы, эквивалентно

построению кода с минимальным расстоянием, не меньшим, чем d. Будем

строить проверочную матрицу Н таким образом. В качестве первого столбца

Н выберем произвольный ненулевой вектор столбец из r-мерного прост-

ранства векторов-столбцов V

(GF(?)). В качестве второго столбца h£ матри-

цы Н возьмём произвольный вектор из множества

= V

(cF(q) )\ j ahf \ а е GF(q).

Если в V,! существует хотя бы один вектор, не являющийся линейной ком-

бинацией hi и , то выберем один из таких векторов в качестве Ьз . Пред-

положим, что таким образом выбраны j векторов: hf,

hj,...,hj\

По построению этих векторов каждый hf (1 ^ i < j) не является линейной

комбинацией никаких d-2 или менее столбцов из hf

,...,hf_j.

Поскольку i векторов из построенных таким образом векторов h|,...,h|

можно выбрать способами, а число способов выбора i ненулевых коэффи-

циентов линейной комбинации равно (#-1)\ то число векторов, являющихся

142

ГЛАВА

IV.

ЛИНЕЙНЫЕ КОДЫ, ИСПРАВЛЯЮЩИЕ

ОШИБКИ

линейными комбинациями

d-2 или

менее столбцов

из hf ,...,hf, не

больше

числа

d-2/^Л

1-а I \

i=l W

которое обозначим посредством Nj(d-2).

Если число Nj(d~2) меньше общего числа

-l

ненулевых векторов

\{о},

то в

(GF(<7)) существует ненулевой вектор,

не

совпадающий

ни с

одной

из

указанных выше линейных комбинаций. Этот вектор можно выбрать

в качестве очередного вектора

}+1

и т.д.

К тому моменту, когда очередной вектор

h„

выбрать

из

множества

\{o},

силу

его

конечности,

уже

нельзя, общее число N

(d-2) линей-

ных комбинаций, порождённых ранее выбранными векторами

(1 < i < п),

удовлетворяет неравенству:

1|^

-1)

-1. (4.2.14)

Добавление нового вектора

числу hf,...,h„ приводит

тому,

что

число линейных комбинаций векторов

hf ,...,hf

впервые превзойдет

-1.

Совокупность

векторов-столбцов

,...,h„ образует проверочную матри-

цу размерности (г х п),

которой любые

d-1

столбцов линейно независимы.

Следовательно, построен

код с

минимальным кодовым расстоянием

по

край-

ней мере

d. А

С целью получить асимптотическое представление границ (4.2.1), (4.2.5),

(4.2.13)

при

больших значениях

воспользуемся оценками Г.Чернова

для

биномиальных коэффициентов.

Теорема

2.4.

Пусть число

удовлетворяет неравенству t<———п.

Тогда справедливы оценки:

„°

<Н

n +

Jto-D^Z^Jfo-l)'**

KnJ

(4.2.15)

См.

Библиографию

[62].

143

§ 2. ГРАНИЦЫ ДЛЯ ПАРАМЕТРОВ КОДОВ

где

(х)

= xlog

(<?-!)-

xlog

- x)log

- х)

Доказательство. Введём производящую функцию:

F(z) = (l + (4-l)z)

= £А

г\ А

| =

i=0

О?-*)

(4.2.16)

Просуммируем коэффициенты по i:

i=0

При

0<z<l,

i<t справедливо неравенство z

>1, используя которое по-

лучим:

i=0

Покажем, что отношение

Ai+i (n-i)(?-l)

(4.2.17)

является монотонно возрас-

тающей функцией по i. Дифференцируя по i это отношение, получаем:

f А Л

i+1

(^-l)(n-i)

При l<i<n производная положительна:

>0.

(<?-1)п „ ..

Так как по условию теоремы t<— , то найдется такое число z

(О

< z < 1), что:

-1

< z <

Так

как

llLr

- < —< z

при 0 < i < t и z < < —

при t < i, то

4+1

i+i

i A

при 0 < i < n

A^AjZ*. (4.2.18)

Покажем справедливость (4.2.18). При i = t нестрогое неравенство (4.2.18)

обращается в равенство.

А-

Пусть i < t. В силу того что —- монотонно возрастающая функция, -

i+i

то

для i < t:

144

ЛАВА IV. ЛИНЕЙНЫЕ КОДЫ, ИСПРАВЛЯЮЩИЕ

ОШИБКИ

—~<—

< z.

Рассматривая произведение (t-i) неравенств вида (4.2.19), получаем:

i A

i+1

AL< -t-i

Aj+i A

i+2

Отсюда следует:

А^<А^. (4.2.20)

A- _

Пусть i > t. Рассмотрим произведение (i

-1)

неравенств вида —— ^ z:

i+i

JL^

t±L

Aj^ A^ ^ _i_

At+i A

t+2

Aj Aj

Отсюда следует:

z'> A

, (4.2.21)

что совместно с неравенством (4.2.20) доказывает справедливость формулы

(4.2.18),

используя которое, получаем:

¥(г) = %Ар

*(п + 1)А

. (42.22)

i=0

Из равенств (4.2.17) и (4.2.22) получаем систему неравенств:

-t

mm —< А

(

< У'А.

min z"'

F(z), (4 2 23)

o<z<:i n +

o<z^i

Обозначим т =

—

и подсчитаем стационарную точку функции

f (z) = z"

F(z) = z~

(l + (q - l)z)

. Найдём производную

введённой функции:

f '(z) = -птг"

(l + [q - l)z)

+ nz~

(l + (q - l^"

(q-1).

Из уравнения f

(z) = 0 находим:

-i[l + (f-l)z]

-l) = 0.

Корень z

уравнения f' (z) = 0 равен:

Zo =

(^-1K1-T)-

(

-24)

При 0 < z < z

имеем производную f

(z) < 0. При z > z

получаем произ-

водную f

(z) > 0. Следовательно, корень z

является точкой минимума.

Подстановкой проверяется, что для t <

——L.

этот корень z

е [oi).

145

§ 2.

ГРАНИЦЫ ДЛЯ ПАРАМЕТРОВ КОДОВ

Значение f(z) в точке z

равно:

f(20)

= *~™(9 - «"

0 - ^)

пт

(1 - тГ

= /

(т)

. («.25)

Из равенства (4.2.25) и системы неравенств (4.2.23) получаем требуемые

оценки (4.2.15). А

Используя теорему 4.2.4, получим асимптотическое представление границ

Хемминга, Плоткина, Варшамова-Гилберта:

п Ч п

(4.2.26)

п п(<?~1)'

(4.2.27)

~>1-Н,

d-2

(4.2.28)

В приведённых формулах Н^(х) - функция, введённая в теореме 4.2.4,

совпадающая с энтропией при q = 2.

Заметим, что утверждения теорем

4.2.1,

4.2.2 справедливы и для нели-

нейных блоковых кодов, так как при их доказательстве не используется факт

линейности кода.

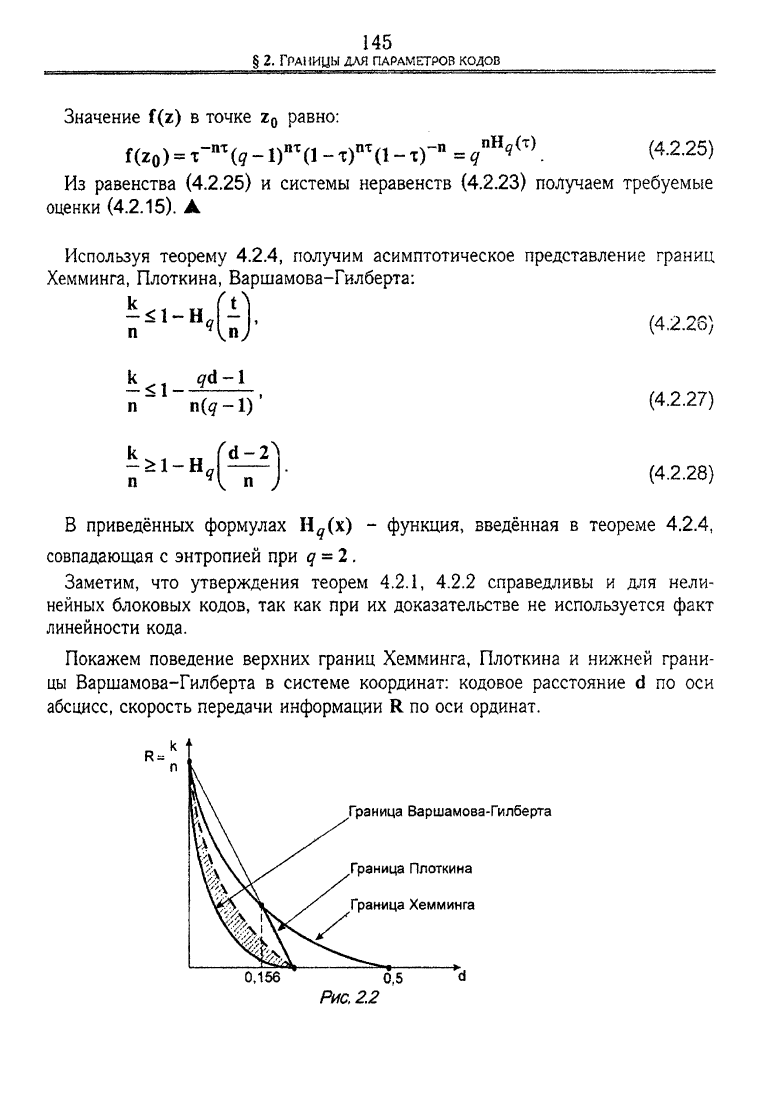
Покажем поведение верхних границ Хемминга, Плоткина и нижней грани-

цы Варшамова-Гилберта в системе координат: кодовое расстояние d по оси

абсцисс, скорость передачи информации R по оси ординат.

Граница Варшамова-Гилберта

Граница Плоткина

Граница Хемминга

0,156

0,5

Рис,

ГЛАВА

IV.

ЛИНЕЙНЫЕ

146

коды.

ИСПРАВЛЯЮЩИЕ

ОШИБКИ

При малых

значениях скорости передачи более точной верхней границей яв-

ляется граница

Плоткина, при больших - Хемминга.

В настоящее время методами линейного программирования для больших п

получена наилучшая верхняя граница Мак-Элиса-Родемича-Рамсея-Велча.

Эта граница

изображена на рисунке 2.2 пунктирной линией. Все коды лежат

не выше

верхней границы Мак-Элиса-Родемича-Рамсея-Велча. Наилучшие

коды лежат

не ниже нижней границы Варшамова-Гилберта. Область

значений параметров, для которых могут существовать коды, отмечена на

рисунке 2.2 штриховкой.

§3

В этом параграфе будут описаны некоторые методы декодирования линей-

ных кодов, основанные на стандартном расположении векторов векторного

пространства V

(GF(^)).

Пусть

- (п,к)-код, g, - нулевой вектор, 12>1з>»**>8 к " остальные кодо-

вые векторы. Процедура декодирования векторов из векторного пространства

, полученных на выходе канала, основана на следующей таблице располо-

жения V

. Кодовые векторы расположим в строку с нулевым вектором слева.

Затем один из оставшихся векторов пространства V

(GF(^)), например

\ц,

помещаем под нулевым вектором

{

Обычно выбирают вектор минимального

веса. Такой вектор наиболее вероятно получить на выходе, если по каналу пе-

редавался нулевой вектор. Вторая строка заполняется так, чтобы под каждым

кодовым вектором gj находился вектор

hi+gj.

Аналогично, в первый столбец

следующей строки помещаем вектор h

минимального веса, не вошедший в

предыдущие строки таблицы. Строка заполняется по правилу: Е

+ &. Процесс

продолжается до тех пор, пока каждый вектор из пространства V

(GF(</)) не

появится в какой-либо из строк таблицы.

Определение

3.1.

Расположение векторов

(GF(q))

в виде

таблицы:

ГС

]

6 +

v„

6 +

, с +

V-

-i,

где G

- (п, кукод,

называется стандарт-

ным расположением.

(4.3.1)

В каждой строке G + hj таблицы V

находятся векторы смежного класса

(GF(<?)) по подпространству G. В первом столбце таблицы (4.3.1) находят-

ся образующие классов смежности. При соответствующем выборе этих обра-

зующих процедура декодирования с использованием стандартного расположе-

ния V

обладает рядом полезных свойств.

МЕТОДЫ ДЕКОДИРОВАНИЯ ПРИ

ПРИМЕНЕНИИ

ЛИНЕЙНЫХ КОДОВ

148

ГЛАВА

IV.

ЛИНЕЙНЫ Е КО

Ы, ИСПРАВЛЯЮЩИЕ

ОШИБКИ

Определение

3.2.

Вектор e = h-g назовём вектором ошибок,

если по каналу связи был послан вектор g, а

получен вектор h.

Если

е = 0, то g = h , и, следовательно, ошибок при передаче не произошло.

Если

е*0, то ненулевые компоненты вектора ошибок ё соответствуют иска-

женным

компонентам кодового вектора g.

Лемма

3.1.

Если стандартное расположение V„ используется как таб-

лица декодирования для линейного (п, к)-кода, то по полу-

ченному вектору h будет правильно декодирован пере-

данный вектор g тогда и только тогда, когда вектор оши-

бок ё = h - g является образующим смежного класса.

Доказательство.

Если

h - g = h;, где h; - образующий i-ro смежного клас-

са, то

вектор

h = hj + g должен находиться в стандартном расположении V

i-м

смежном классе

под кодовым словом g и поэтому будет правильно де-

кодирован. Если

же вектор h-g не является образующим смежного класса,

то вектор

Ь должен находиться в некотором смежном классе, например, j-м, с

образующим gj. Тогда вектор h расположен в j-й строке, но не под вектором.

g, потому что h Ф hj + g . А

Декодирование полученного вектора h с использованием определения таб-

лицы

стандартного расположения (см. определение 4.3.1) осуществляется сле-

дующим

образом. Вектор h находится в одной из строк, например в i-й. Из

него

вычитается вектор hj - образующий этого класса смежности. Тогда

- hj е

объявляется переданным кодовым вектором. Заметим, что несмотря

на простоту

метода декодирования, он является неприемлемым для реальных

линейных

кодов,

когда

значения параметров кодов k, п достигают значений

О(10

Требуемая для его реализации память п^

весьма велика. Она

равна

п2

единиц

двоичной информации при q = 2.

Рассмотрим модификацию этого метода. Пусть (п, к)-код G является ортого-

нальным

пространством матрицы H((n-k)xn).

149

МЕТОДЫ

ДЕКОДИРОВАНИЯ ЛИНЕЙНЫХ КОДОВ

Определение 3.3. Для любого полученного на выходе канала

вектора h вектор

S(h) = hH

называется синдромом.

(4.3.2)

Так как G - ортогональное пространство матрицы Н, то h е

тогда и толь-

—

— т —

ко тогда, когда произведение S(h) = hH = 0.

Лемма 3.2. Два вектора hj,h

принадлежат одному и тому же смеж-

ному классу тогда и только тогда, когда их синдромы рае-

ны.

Доказательство. Два вектора h

принадлежат одному смежному классу,

если их разность принадлежит

То есть (hj -h

)Jl

=0. Так как для опе-

раций с матрицами справедлив дистрибутивный закон, то:

-h

)Н

= h

{

- Н

= 0 .

Следовательно,

S(h,) = S(h

). А

Процесс декодирования может быть сильно упрощён за счет использования

таблицы соответствия образующих смежного класса и синдромов для каждого

из 2 классов смежности. После того как на выходе канала получен вектор

К, вычисляется его синдром S(h). Затем по таблице отыскивается соответст-

вующий ему вектор-образующий смежного класса, который является предпо-

лагаемым набором ошибок. Вычитание его из h даёт, предположительно,

посланный кодовый вектор. Объём памяти, необходимый для декодирования с

использованием синдромов, равен n2

+(n-k)2

+n(n - к), что сущест-

венно меньше, чем в первом случае с использованием таблицы стандартного

расположения V

Теорема 3.1. Пусть G -(п, к)-код, используемый для передачи по двоич-

ному симметричному каналу. Пусть все кодовые векторы

имеют одну и ту же вероятность быть переданными.

Тогда средняя вероятность правильного декодирования

совпадает с наибольшей возможной вероятностью для

этого кода, если в качестве таблицы декодирования ис-

150

ГЛАВА

IV. ЛИНЕЙНЫЕ КОДЫ, ИСПРАВЛЯЮЩИЕ

ОШИБКИ

пользуется стандартное расположение, в котором каж-

дый образующий вектор смежного класса имеет мини-

мальный вес в своём классе.

Доказательство. Пусть hjj - вектор, стоящий в i-й строке и j-м столбце

таблицы декодирования. Кодовое слово в верхней строке j-ro столбца обоз-

начим g

j. Пусть d

j =d(hjj,g

j). Вероятность правильного декодирования, ес-

ли был передан вектор g

j, равна:

I P

,ij

. (4.3.3)

где p - вероятность ошибки в канале, q =

- р - вероятность правильной пе-

редачи в канале.

Так как имеется 2

кодовых векторов, которые используются равнове-

роятностно, то при усреднении вероятности правильного декодирования по

всему коду

получаем:

-l

Рс-т I .1 pW (4.3.4)

Каждому возможному двоичному вектору на выходе канала в этой сумме

соответствует одно слагаемое; каждое из этих слагаемых принимает макси-

мальное значение, если соответствующий вектор декодируется в ближайший

кодовый вектор в смысле метрики Хемминга, так как p

*q°

* - монотонно

убывающая функция от расстояния dy. Поэтому вероятность правильного де-

кодирования будет максимальной, если каждый полученный вектор будет де-

кодирован в ближайший кодовый вектор.

Предположим теперь, что некоторый вектор h расположен в таблице де-

кодирования под кодовым вектором g так, что d(h,g) = W. Допустим, что

ближайший кодовый вектор gj находится на расстоянии Wj от h. Пусть f

образующий смежного класса, содержащего вектор К. Тогда вес вектора

f =

йI"

- g равен W. Элемент h - gj = f + (g - gi) имеет вес W

и лежит в том

же самом смежном классе. Поскольку предполагалось, что f имеет мини-

мальный вес в своем смежном классе, то Щ £ W, и поэтому h лежит, по

крайней мере, так же близко к g, как и к gj. •