Духин А.А. Теория информации

Подождите немного. Документ загружается.

101

Второй метод

(Метод К. Шеннона). Рассмотрим источник

[A,jp(s)]:

Упорядочиваем буквы алфавита А по убыванию их вероятностей.

Находим числа £

i =

1,...,п,

исходя из условия:

^zp (3.2.4)

Подсчитываем накопленные суммы:

п-1

Pi =0, Р

=p(

), Р

=р(а

) + р(а

),... Р„ = Ip(aj).

(3>2

.5)

i=l

Находим первые после запятой £

{

знаков в разложении числа Р

{

в двоич-

ную дробь: i =

l,,..,n.

Цифры этого разложения, стоящие после запятой,

являются кодовым словом, соответствующим букве a

Если необходимо, производим операцию усечения.

Замечание 2.1. Рассмотренный код обладает свойствами префикса. Рас-

смотрим два слова а^гц» i'>i. В силу неравенства (3.2.4):

Р,'-Р^Р

1-Р.=Р(а|)^-

2 *

Следовательно, двоичные разложения чисел Pj и отличаются не далее

чем в позиции с номером £

. Ясно, что £[<£\. Кодовые слова

aj,5j'

разли-

чаются не далее чем в £

{

-й букве, то есть одно из них не является началом

другого.

Замечание 2.2. Оценим среднюю длину кодовых слов, построенных с ис-

пользованием метода К. Шеннона. Из неравенства (3.2.4)

вытекает: £

{

<- /ogPj +1.

Усредняя по алфавиту А, получаем:

^ср

= £р(»1)'| <- £p(»i)/<KPi + £р(»|) = He +1,

i=l 1=1 1=1

где = Н(А) - энтропия рассматриваемого источника без памяти.

Для сравнения методов рассмотрим тот же самый источник и проделаем

Р(а,)

Р.

а 1

»i 0,36

0,00 00 00

0,18

3 0,36 = 0,010 010 01

0,18

0,54

0,100 100 100

»4

0,12 4

0,72 = 0,1011 1011 101

0,09

0,84 = 0,1101

1101 110

0,07

0,93=0,1110 1110 111

§ 2. ПРОСТЕЙШИЕ МЕТОДЫ ПОСТРОЕНИЯ ПРЕФИКСНЫХ КОДОВ

102

ГЛАВА

III. ОПТИМАЛЬНОЕ КОДИРОВАНИЕ

где | a ij - код, полученный на 4-м шаге алгоритма, к которому не

применена операция усечения, {aj - код, полученный после операции

усечения. Средняя длина для построенного кода £

ср

= 2,46.

Соответствующее кодовое дерево имеет вид:

а, а

Для сравнения напомним,

что средняя длина слова

для метода Фано

2,44.

Рис.

2.2

Замечание

3.2.3. Рассмотренный алгоритм Р. Фано в случае распределения

на алфавите источника, задаваемого отрицательными степе-

нями двойки, позволяет при каждом разбиении на подгруп-

пы получать равенство суммарных вероятностей, входящих

в любую из подгрупп. Следовательно, число двоичных сим-

волов в кодовом слове будет равняться собственной инфор-

мации соответствующей буквы источника. Отсюда вытекает,

что усреднённое по алфавиту источника число двоичных

символов на сообщении будет равно энтропии источника

Н(А).

Таким образом, для энтропии источника мы получаем

важную интерпретацию: Н(А) - нижняя грань для средней

длины кодовых слов, достижимая для указанных распреде-

лений.

Если же распределение на алфавите таково, что для некоторых разбиений

нельзя образовать равновероятные группы, то метод Фано необязательно

приводит к минимальной длине кодовых слов.

Замечание

3.2.4. Рассмотренные выше методы построения кодов могут быть

использованы с незначительными изменениями в случае

D -чных алфавитов.

§3

В этом параграфе рассмотрим построение оптимальных двоичных кодов ме-

тодом Хаффмана. Решается задача кодирования источника без памяти,

[A,p(s)],

порождающего буквы

..,a

с вероятностями р^-^Рп- Без

ограничения общности будем предполагать, что эти вероятности упорядочены

по убыванию: pj > р

>... ^ р

. Требуется построить двоичный код с

минимальной средней длиной.

Приведём свойства оптимального кода для вероятностных распределений на

алфавите А источника, отличных от равномерного.

Лемма 3.1. В оптимальном коде длины £

{

кодовых слов гц не убывают,

то есть:

£^<£

^...^£

. (3.3.1)

Доказательство. Доказательство проведём от противного. Пусть исходный

код оптимальный и для него при условии Pj>Pj (i<j) выполняется неравен-

ство (

>£-

Построим новый код, приписав кодовое слово Sj букве а

и ко-

довое слово а

}

букве aj. Остальные соответствия букв словам оставим без из-

менения. Сравним среднюю длину исходного кода £

ср

и среднюю длину пост-

роенного кода £'

ср

<с

-<р=Pi'i + Р/j - P/i - Pi^j = (Pi - PjX'i - 'j) >o.

Следовательно, построенный код имеет меньшую среднюю длину, чем ис-

ходный, что противоречит его оптимальности. А

Лемма 3.2. Существует оптимальный префиксный код, в котором двум

наименее вероятным буквам a

_j, а

соответствуют кодо-

вые слова, имеющие одинаковую длину и различающиеся лишь

в последнем разряде.

Доказательство. Рассмотрим оптимальный префиксный код и соответст-

вующее ему дерево. Обозначим а' вершину дерева, предшествующую а

. Из

вершины а' обязательно выходит два ребра с концевыми вершинами ъ

, а

В противном случае рассмотренный код не был бы оптимальным. Таким обра-

зом, концевым вершинам а^а,, и a

_j соответствуют кодовые слова с длина-

ПОСТРОЕНИЕ

ОПТИМАЛЬНЫХ КОДОВ МЕТОДОМ ХАФФМАНА

104

ГЛАВА

III.

ОПТИМАЛЬНОЕ

КОДИРО

В AH И Е

ми

и £

_!, согласно лемме 3.3.1 удовлетворяющие неравенству

С другой стороны, так как 1

=£

; то £

-£

^. Если вершина a

соответ-

ствует букве а

отличная от a

, то, поменяв местами ^ и а

добьёмся

того,

что вершинам а

п-1

и а

будет предшествовать одна и та же вершина

а'. После перестановки новый код будет оставаться оптимальным и, кроме то-

го,

будет обладать свойством, указанным в формулировке леммы 3.3.2. А

Построим новый источник А', полученный из исходного источника А

"склеиванием" наименее вероятных букв a

и а

в букву а'. В источнике

сообщений А' буквы

.„,a

порождаются с вероятностями, совпадающи-

ми с вероятностями этих букв в источнике А, а буква а' имеет вероятность

Рп-1

Рп-

Новый источник А' называется редуцированным. Операцию реду-

цирования (склеивания) можно проводить конечное число раз до тех пор, пока

алфавит источника не будет состоять из одной буквы, порождаемой с вероят-

ностью единица.

Имея код, отвечающий редуцированному источнику А', можно построить

код, отвечающий исходному источнику А. Пусть буквам алфавита А' сопос-

тавлены слова

а,,...,а

,а'.

Тогда для алфавита А = {aj,...,а

} исходного ис-

точника построим код следующим образом. Для букв

..,a

сохраним ко-

довые слова

..,a

а в качестве а^Дп возьмём слова, полученные в ре-

зультате дописывания к а' символов 0 и 1, соответственно.

Лемма

3.3.

Если префиксный код для редуцированного источника А'

является оптимальным, то и код для исходного источника

А,

построенный указанным способом, также будет опти-

мальным.

Доказательство. Положим, что средняя длина кодовых слов редуцирован-

ного источника А' равна £'

ср

, а для исходного источника - £

с?

. Найдём соот-

ношение между этими средними длинами, принимая во внимание, что

^n-i^n =^' +

где £' - длина слова а' и p' = p

-i +

л п-2

^ср = £Р^ = £PI'i + P„-i(*' +1) + Р„(^ +1) = (3.3.2)

п-2

= + Р

+ Рп-1 + Рп = ^ср + Рп-1 + Рп

•

105

§ 3. ПОСТРОЕНИЕ ОПТИМАЛЬНЫХ

КОДОВ

МЕТОДОМ

ХАФФМАНА

Пусть код для алфавита А исходного источника не является оптимальным,

тогда рассмотрим оптимальный код, удовлетворяющий лемме 3.3.2, и пост-

роим по нему код для редуцированного источника, сопоставив букве а'

вершину а', предшествующую вершинам а

п-1

, а

, и сохранив за остальными

буквами а

(i =

1,...,п-2)

те же кодовые слова a

что и в оптимальном коде.

Обозначим средние длины кодовых слов для этой новой пары кодов £^ и £

Для этих чисел справедливо соотношение:

При этом ^

ср

следовательно, должно выполняться неравенство

^ср

^ср'

что п

0ТИВ0

ечит

оптимальности кода, построенного для редуциро-

ванного источника. А

Опишем алгоритм Хаффмана для построения кодов. Этот алгоритм всегда

приводит к построению оптимального множества кодовых слов, в том смысле,

что никакое другое множество не имеет меньшего среднего числа символов

на букву алфавита А.

Для любого источника все наборы кодовых слов, удовлетворяющие

приведнным выше условиям, дают одну и ту же среднюю длину кодового

слова. Алгоритм Хаффмана дат возможность построить по крайней мере один

из таких наборов.

Леммы 3.3.1 и 3.3.2 требуют, чтобы две наименее вероятные буквы

были сопоставлены концевым вершинам одинакового и максимального

порядка, порождаемым одной и той же промежуточной вершиной

предыдущего порядка. В силу леммы 3.3.3 каждый источник кодируется

оптимальным кодом, так как редуцированный источник был кодирован

оптимально. Последовательная реализация этих лемм обеспечивает

построение оптимального кода методом Хаффмана.

Построение оптимального кода методом Хаффмана сводится к выполнению

двух частей алгоритма.

Алгоритм

I. Построение последовательности редуцированных источников, сходящейся к

вырожденному источнику:

Буквы источника располагаем в порядке убывания вероятностей.

Две наименее вероятные буквы склеиваем в одну букву редуцированного

источника и приписываем этой букве суммарную вероятность склеенных

букв.

Переходим к первому пункту, если алфавит редуцированного источника

состоит из двух или более букв. В противном случае, переходим ко вто-

рой части.

106

ГЛАВА

Ш. ОПТИМАЛЬНОЕ КОДИРОВАНИЕ

II.

Построение кодового дерева и соответствующего оптимального кода:

Проводим рёбра, соединяющие буквы в алфавитах последовательных ре-

дуцированных источников, и получаем граф-дерево, в котором буквы исход-

ного источника являются концевыми вершинами дерева, а единственная

буква последнего вырожденного источника соответствует корню дерева. По-

мечаем построенные рёбра метками из алфавита В = {o,l} и прослеживаем

эти метки при движении от корня дерева к концевой вершине. В итоге по-

лучим кодовое слово, соответствующее букве исходного алфавита. А

Так как буквы сопоставляются только концевым узлам, то такое кодирова-

ние приводит к префиксному коду.

Сформулированный алгоритм однозначно приводит к оптимальному множе-

ству кодовых слов, за исключением того случая, когда в исходном источнике

или в последующих редуцированных источниках имеется более двух букв с

равными и минимальными вероятностями.

Располагая в другом порядке буквы редуцированных алфавитов, можем по-

лучить также оптимальные префиксные коды с набором кодовых слов тех же

длин, что и в рассмотренном примере. Коды будут различаться самими кодо-

выми словами.

Проиллюстрируем работу алгоритма на примерах. Рассматривается источ-

ник без памяти: А = {a

.,,a

} и jp(s)= (0.3,0.2,0.15,0.15,0.1,0.05,0.05). Ис-

пользуя алгоритм Хаффмана, построим оптимальный код:

Л)

Р(а.) А, А

А,

Ав А

5 6

а а

° ~

а,

0,3

а,

0,2

3 2 Эг

0,15

а<

0,15

0,1

1 2

А а

0,05

,аа I а,

1 2

А а

Рис.

3.1

107

§ 3. ПОСТРОЕНИЕ ОПТИМАЛЬНЫХ КОДОВ МЕТОДОМ

ХАФФМАНА

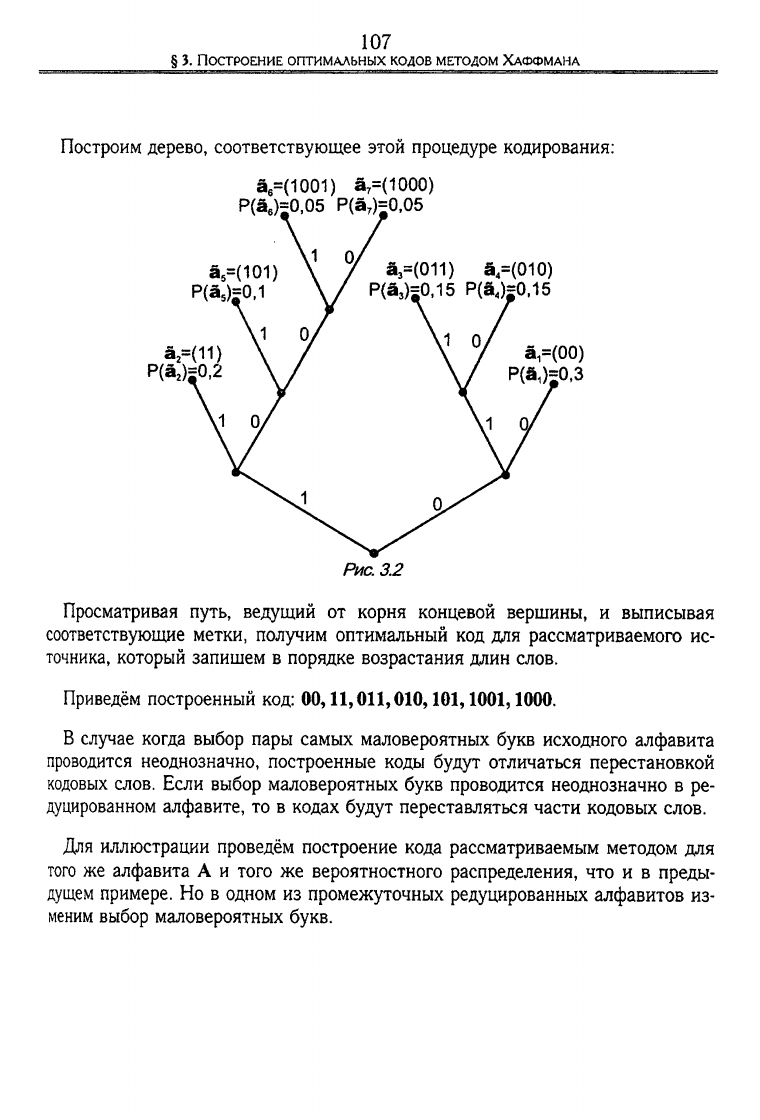
Построим дерево, соответствующее этой процедуре кодирования:

=(1001)

=(1000)

Рис.

3.2

Просматривая путь, ведущий от корня концевой вершины, и выписывая

соответствующие метки, получим оптимальный код для рассматриваемого ис-

точника, который запишем в порядке возрастания длин слов.

Приведём построенный код: 00,11,011,010,101,1001,1000.

В случае когда выбор пары самых маловероятных букв исходного алфавита

проводится неоднозначно, построенные коды будут отличаться перестановкой

кодовых слов. Если выбор маловероятных букв проводится неоднозначно в ре-

дуцированном алфавите, то в кодах будут переставляться части кодовых слов.

Для иллюстрации проведём построение кода рассматриваемым методом для

того же алфавита А и того же вероятностного распределения, что и в преды-

дущем примере. Но в одном из промежуточных редуцированных алфавитов из-

меним выбор маловероятных букв.

108

ГЛАВА

III. ОПТИМАЛЬНОЕ

КОДИРОВАНИЕ

P(a

)

а, 0,3

0,2 •

а, 0,15

0,15 *~

а, 0,1

0,05

А,

а?

5г

ЯНЕ

3.3

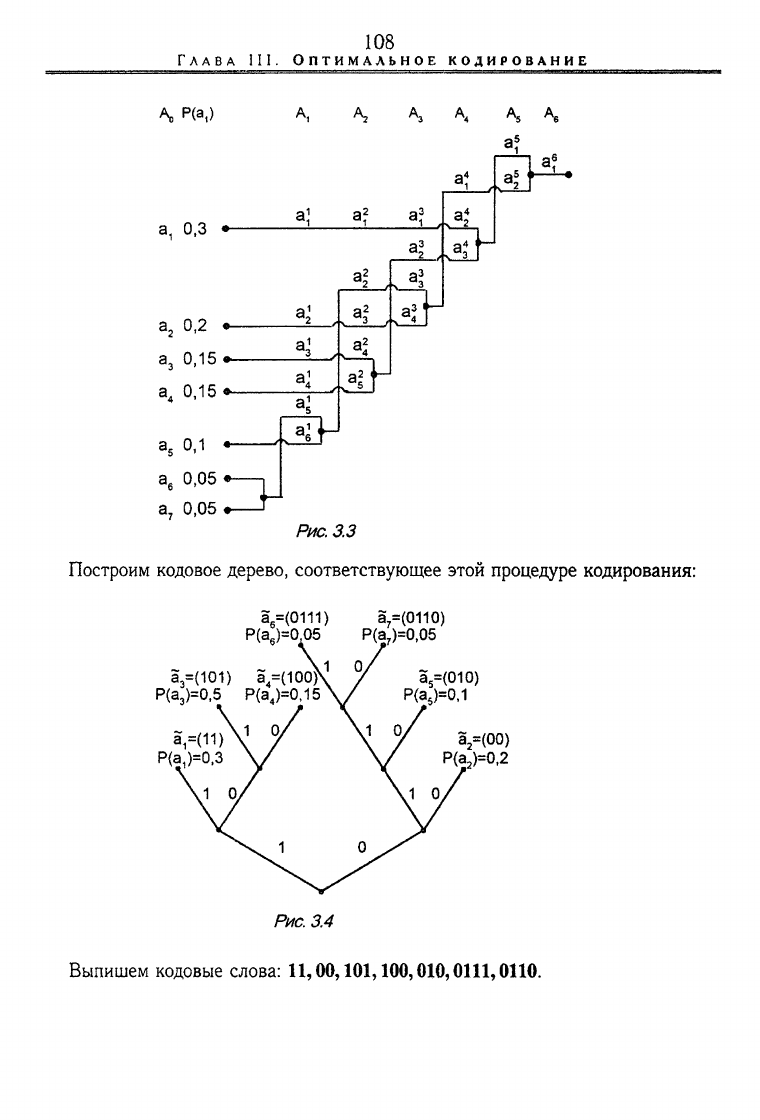
Построим кодовое дерево, соответствующее этой процедуре кодирования:

а =(0111) §=(0110)

Р(а

)=0,05 Р(а

)=0,05

а=(101)

a=(10oY

Р(а

)=0,5

Р(а

)=0,15

а,=(11)

Р(а,)=0,3

VK010)

Р(а

)=0,1

=(00)

Р(а

)=0,2

Рис.

3.4

Выпишем кодовые слова: 11,00,101,100,010,0111,0110.

109

§ 3.

ПОСТРОЕНИЕ

ОПТИМАЛЬНЫХ

КОДОВ

МЕТОДОМ

ХАФФМАНА

Замечание 3.1. Приведём алгоритм Хаффмана для построения оптимальных

префиксных кодов в случае, когда

|В|

= D > 2.

Алгоритм:

Буквы источника располагаем в порядке убывания вероятностей.

Пусть натуральное число r

е N) удовлетворяет двум условиям:

2^r

<D, (3.3.4)

При этом, если D = 2, то г

= 2.

Склеиваем в одну букву г

наименее вероятных букв исходного источника

и приписываем полученной букве суммарную вероятность.

Упорядочиваем по убыванию вероятностей буквы редуцированного источ-

ника.

Склеиваем D наименее вероятных букв редуцированного источника в одну

и приписываем полученной букве суммарную вероятность склеенных букв.

Переходим к пункту 3, если алфавит редуцированного источника состоит

более чем из одной буквы. В противном случае алгоритм прекращает свою

работу.

6. Проводим рёбра, соединяющие буквы в алфавитах последовательных

редуцированных источников, и получаем граф-дерево, в котором концевым

вершинам соответствуют буквы исходного источника. Помечаем построен-

ные рёбра метками из алфавита В =

{o,l,...,D-l}

и прослеживаем эти мет-

ки при движении от корня дерева к концевой вершине. В итоге получаем

набор кодовых слов для алфавита исходного источника. •

по

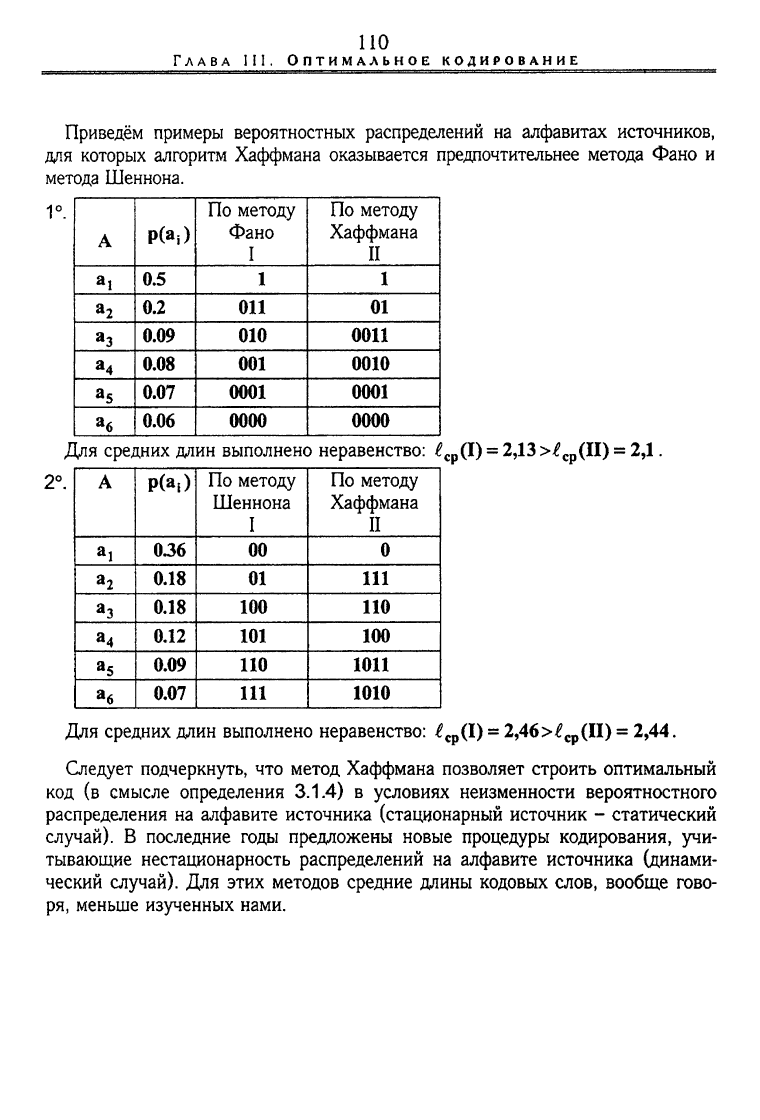
Приведем примеры вероятностных распределений на алфавитах источников,

для которых алгоритм Хаффмана оказывается предпочтительнее метода Фано и

метода Шеннона.

1°.

По методу

Фано

По методу

Хаффмана

0.5 1 1

0.2 011 01

0.09 010

ООП

0.08 001 0010

0.07

0001

0.06

0000 0000

Для средних длин выполнено неравенство: ^

ср

(1) = 2,13

>£

ср

(11)

= 2,1.

2°.

По методу

Шеннона

По методу

Хаффмана

036 00 0

0.18 01 111

0.18

100

ПО

0.12 101

100

0.09 по юн

0.07 111

1010

Для средних длин выполнено неравенство: ^

ср

(1) = 2,46>^

ср

(П) = 2,44.

Следует подчеркнуть, что метод Хаффмана позволяет строить оптимальный

код (в смысле определения 3.1.4) в условиях неизменности вероятностного

распределения на алфавите источника (стационарный источник - статический

случай). В последние годы предложены новые процедуры кодирования, учи-

тывающие нестационарность распределений на алфавите источника (динами-

ческий случай). Для этих методов средние длины кодовых слов, вообще гово-

ря,

меньше изученных нами.

ГЛАВА

III. ОПТИМАЛЬНОЕ КОДИРОВАНИЕ