Духин А.А. Теория информации

Подождите немного. Документ загружается.

§ 3.

МАРКОВСКИЕ

ИСТОЧНИКИ

p(C^)

p(a

)p(a

)...

(2.3.13')

ПГА-

/А- А ^ ТТ

JM-L

JM>)

J1 JM

•"

"m-l

/ai

m-2'-'

ftr"'

JM/

Теорема 3.2. Для любых e>0, r|>0 существует £

такое, что при

£>£

, все реализации длины £ источника [A,p(s)] могут

быть разбиты на два класса:

Q = C'i + .

Для любой последовательности е имеет место:

гЛ?

оо =- I p(

-a

)fogp(a

/а

|1в-1

,...,а

)

энтропия источника сообщений. Суммарная вероятность

последовательностей из С" меньше 8.

Доказательство. Зададимся произвольными е > 0, т| > 0. Разобьём все реали-

зации C

на два класса по следующему правилу. К первому классу C'

отне-

сём те и только те последовательности, для которых:

,JM

-W

JL>P<

JL)~P<

JM-L'~'

IL>H

)

и p(C^)>0. Ко второму классу С" отнесём все последовательности, для кото-

рых неравенство (2.3.15) не выполняется, по крайней мере, для одной частоты

m-граммы.

Пусть

с'

еС

Тогда неравенство (2.3.15) может быть записано в эквива-

лентной форме:

JL,~.JM

4»<

>P(

/А

>-P<

JM-L

'~'

(2.3.16)

h~hn

™K JmH

Подставим представление для

, задаваемое равенством

(2.3.16),

(2.3.13*)

р(С',) = р(а

(

, )p(a

/а,,)... P(a

_, /а

1т

,...,л-

)

Jm-i '-'

Р(а

п )

Р(1

т /aim_1

)+tS@n

(

Jl'"-

Jm)

Выполним ряд преобразований:

°g-TTZ

= -

fcgp(aj,)

~logp(a

/а,,)

-...

p(Cf)

EP(

>P<

Ji )-P(

-i

'-'

SP<

Jm /a

,-,ад )-

№

Jb...,im

-l

'-'

h)-

Разделив

обе

части равенства

на £ у.

воспользовавшись формулой (2.3.5),

получаем:

Hw =

^^il

Р<

'2 '"I, )-Р(«1

/»1

•••»„

)]

+ 8

У©м i log .

(ajj .-,aj

)

Jm Jm-1' ' Jl'

i,'-»,a

_,)

Далее получаем:

log—--H

P(c<)

80 2>g — .

(aj

...,

aJm

)P<

Jm-l'-'

Jl)

где

0= max \&„ , \.

(i i

Jm)

'~'

Jm|

Так как

(

C'<,,

то

-l)

Jm-l'-'

Jl>

Выбирая

—

log—

|_Т|

р(а,,

,...,а

1т

_,)

получаем:

P(Cf)

£ ~

(

ajl

,...,a

)

Jm-l'-'

il)

(2.3.17)

Л ABA

II.

ИСТОЧНИКИ С ООЕЩЕНИЙ

§ 3,

МАРКОВСКИЕ

ИСТОЧНИКИ

Докажем второе утверждение теоремы. Имеет место оценка:

I р{

K,...,j

-^р(аи)р(а

/•

)..4Kaj

„ш^ыь].

Л '~>

Зафиксируем индексы (j,,...J

). Согласно закону больших чисел

для лю-

бых 8 > 0,

е' >

достаточно большого

имеет место:

p{|

mjl

-^(

ajl

)|<iU}>l-e'.

(2318)

Если (2.3.18) имеет место,

то

достаточно велико,

и в

силу закона боль-

ших чисел справедлива оценка

Jli2

-P(a

) <- >1-г'.

Это неравенство эквивалентно следующему:

{Ьт

/а

л i <

•

При выполнении неравенства

скобках имеем:

{Ь.J2J3

JIJ

i2Jl

< ^} >

•

Рассуждая аналогично, получим

еще ряд

неравенств:

JlJ2J3J4 "

Jl J2J3 P<

J3J2il

^ Л

Б'.

JlJ2J3

J3J2J1'

(2.3.19)

(2.3.20)

(2.3.21)

{hi,...j

J,-J

-l

^1т-2...пЬ^}>^'

2322

Jb...,J

Jb...,im-lP<

J«-l--'

Jl)|

(2-

)

Из соотношений (2.3.18)-(2.3.23) получим простые следствия:

JlP<

)-P(

Jm-l '""

" *

>P^

>'"

-P(

J»-l'-»

il)|

( i

Jli

J2Jl)-P(

Jm-l'""

Jl)-

ilP(

il>'"

ГЛАВА

II.

Источники

СООБЩЕНИЙ

(

JlJ2J3^

J3J2Jl

)"'P(

Jm-l

jl >"

J!J2^

>"'

••p(

-,'-'

J«)i

Jl,...,j

-lP(

-i

Jl)-

Jb-,im-2P<

-l

-2,-il

P(«J«

*Jm-l~

Jl)|

Pllmii

i .i

-m

i. i iP(

i i i. )l

<—^i>l-e'.

Jl—Jm-lJm

Jl-Jm-l

Jm-l-Jl'l

Вероятность совместного выполнения неравенств в скобках больше, чем

(l -

г'У"

- те'. Следовательно, вероятность выполнения неравенства

J.-

-^P<

il >P<

)™P(

Jm-l

"~'

>l < ~* '

полученного путём сложения приведённых выше неравенств, также будет

больше

j те'. А поэтому получаем:

I K,~Jm -^<

Ji>P(

Jl)"P<

Jm-l'~'

JI^

}

<ms

Суммируя, имеем:

ЕР I K,...,Jm

Ji)P(

h>-P<

Jm-l'-»

Jl>l^

(

J1 "

<me'n

Выбирая s' = (величины тип фиксированные), получаем доказатель-

ство теоремы. А

Из доказанной теоремы следует, что марковские источники обладают ин-

формационной устойчивостью, или, что равносильно, свойством равнораспре-

делённости:

-«н

в)+

л)<

р(с

)<а

-«н.-г

Это свойство позволяет оценить число последовательностей, вошедших в

первый класс .

Так как вторая теорема Шеннона для марковских источников формули-

руется и доказывается аналогично второй теореме Шеннона для источников

без памяти, то доказательство её опустим.

§4

При рассмотрении источников без памяти и марковских источников в пер-

вой теореме Шеннона была показана информационная устойчивость последо-

вательностей, входящих в класс С'ц. Имеется широкий класс источников

более общей природы, для которых это свойство устойчивости также имеет

место. Это так называемые эргодические источники сообщений. В теореме,

доказанной Мак-Милланом, свойство информационной устойчивости

перенесено на реализации, порождаемые этим классом источников.

Определение

4.1. Дискретный стационарный источник [A,p(s)]

называется эргодическим, если любое изме-

римое относительно вероятностной меры p(s),

заданной на F

, инвариантное по сдвигу множе-

ство последовательностей, порождённых источ-

ником, имеет вероятность либо единица, либо

нуль.

Хотя приведённое определение является весьма изящным, однако с ним до-

вольно трудно работать. Следующее эквивалентное определение будет свобод-

но

от этого недостатка. Формулировка его опирается на известную эргодичес-

кую

теорему Биркгофа

Рассмотрим действительнозначную функцию f(х),х = (xj...х^), keN,

определённую для каждого элементарного цилиндра а, измеримую относи-

тельно вероятностной меры p(s). f(a) - случайная величина. Предположим,

что f(a) суммируема, то есть существует математическое ожидание

Ef(a)= Jf(a)dp(a)

. (2.4.1)

Теорема

Биркгофа.

Для любого дискретного стационарного источника

[A,p(s)] и всякой суммируемой функции f(a) суще-

ствует почти всюду предел

/fm

±|>(Т

а)

= Ь(а-), (2.4.2)

См. Библиографию [8].

Определение А' см на с. 52.

ЭРГОДИЧЕСКИЕ

ИСТОЧНИКИ.

ТЕОРЕМА

МАК-МИЛЛАНА

ГЛАВА

II.

Источники

СООБЩЕНИЙ

где Т

а - к-й сдвиг цилиндра a, a h(a) инвариант-

на относительно сдвига для всех а е А

, на которых

этот предел существует.

Определение

4.2. Дискретный стационарный источник JA,p(s)]

называется эргодическим, если почти всюду

h(a) = Ef(a).

Для проверки свойства эргодичности источника [A,p(s)] следует убедиться,

что для функции f(x) = f(x

..,x

),keN - произвольной, измеримой,

суммируемой, и для любых е > 0, 8 > 0 найдётся такое L, что при I

L будет

выполняться закон больших чисел:

^f(x

i+1

,...,x

i+k

)-Ef(x)

i=0

Свойство эргодичности позволяет для любой произвольной суммируемой

f(x) находить вероятностные характеристики источника при соответствующем

подборе функции.

Рассмотрим ряд примеров.

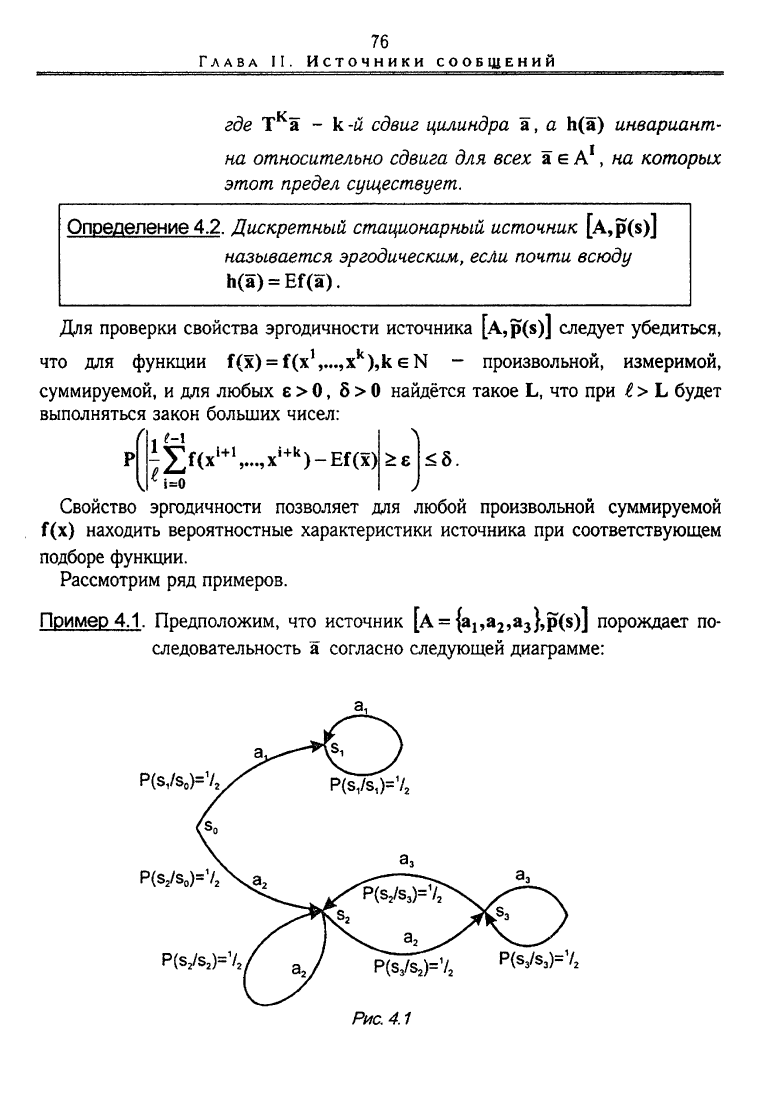
Пример

4.1.

Предположим, что источник [A = {a

},p(s)] порождает по-

следовательность а согласно следующей диаграмме:

)=7

;

P(s

)=7

P(s

)=7,

P(s

)=7

§ 4.

ЭРГОДИЧЕСКИЕ

ИСТОЧНИКИ.

ТЕОРЕМА

МАК-МИЛЛАНА

Попав с вероятностью ~ в состояние S

источник будет по-

рождать бесконечную последовательность а = (а

,а

,...).

Попав с вероятностью — в состояние S

, источник будет по-

рождать всевозможные последовательности, составленные из букв

,а

Этот источник имеет два устойчивых типа поведения, та-

ких, что с вероятностью ~ в любом из них он порождает инва-

риантные, относительно сдвига множества последовательностей.

Согласно определению

(2.4.1)

источник не является эргодическим.

Пример

4.2.

Источник, рассмотренный в примере

2.4.1,

очевидно, является

эргодическим в силу определения

2.4.1.

Пример

4.3.

Используя определение

2.4.2,

покажем, что источник без памяти

эргодический.

Теорема

4.1.

Всякий источник без памяти является эргодическим.

Доказательство.

Пусть f(x) = f(x

,...,x

),k€N - произвольная измеримая

функция. Пусть

- km. Обозначим:

=Г(х

,...,х

|+к

), i = 0,W-l

Ft=Y*

i=0

Рассмотрим

£-1

1-Х к m к

f, -

£f

,...,x

i+k

)=£f,

= ££f ((. - i)k +

i=0 i=0 j=ls=l j=l

где

((

)

Заметим, что

для |i-j|^k являются к-зависимыми случайными вели-

чинами. Введённые случайные величины hj, j =

l,...,m

позволяют рассматри-

вать их в виде суммы независимых одинаково распределённых случайных ве-

личин, так как для различных j случайные величины Ц зависят от непересе-

кающихся наборов независимых случайных величин

ГЛАВА

II.

Источники

СООБЩЕНИЙ

•Ef(x)

= Р

j=1

>е

<Р

hj-Ef(x)|

хотя бы при одном j

Так как случайные величины hj, j =

l,...,k

одинаково распределены, то

-f-Ef(i) >е = кР

—h

-Ef(x)

)

—h

-Ef(x)

Так как для последовательности случайных величин hj можно применить

закон больших чисел, то при достаточно большом m (k-фиксированная вели-

чина) правая часть неравенства может быть сделана не более наперед задан-

ного 6 > 0. То есть для выполнено определение 2.4.2. А

Отказавшись от предположения марковости, введём для стационарных

источников такие характеристики.

Определение4.3. Назовем энтропией источника на

знак величину

Н/=™ yp(cj)kgp(c,).

(2.4.3)

Определение4.4. Назовем шаговой энтропией

источника величину

=- £

рСа^

,...,а^ )/о£р(а^ /а,,

,...,а

) =

—

Н(а^ /а

{)

i£_j)

•

(2.4.4)

Лемма 4.1. Шаговая энтропия и энтропия на знак дискретного ста-

ционарного источника являются не возрастающими после-

довательностями.

Имеет место соотношение

Urn Ui=lim Н

= Н

, (2.4.5)

if—>ао

где - энтропия источника, определённая формулой (2.1.5).

§ 4. ЭРГОДИЧЕСКИЕ

ИСТОЧНИКИ.

ТЕОРЕМА МАК-МИЛЛАНА

Доказательство.

Согласно

(1.2.15)

H(a

i<?

/а

,...,a

) < Н(а^ /а

у...,*^

Используя стационарность источника, получаем:

Н<° = Н(а

, /a

,...,а,

) < Ща,^ /а^

„..,а

1м

)

= Н<^>.

Заметим, что Н

> Н

(£)

Покажем, что энтропия на знак тоже не возрастающая последователь-

ность.

1 1 1

~ j]£P(

«P(^) =-H(C^_i) + -Н (а^ /a

,.»>а^_, ) =

е 1-1

£ £ £

Отсюда следует:

1 1-1

Докажем второе утверждение леммы.

7^-т[н(а^

/а,,

-.,a

)

Н(а

|/+1

/а

, ,...,а

,) + H(a

if+j

/а

,...,а

, )]<

последнем неравенстве перейдём к пределу по

< H(a

/а,, ,...,а^_,) = H

. (2.4.6)

Так как (2.4.6) справедливо для всех £, то, переходя к пределу по I, получаем:

< lim Н

. (2.4.7)

другой стороны:

н, Л [н

(,)

+Н

>+...+H

]> -Н«> = Н<°.

Переходя в полученном соотношении к пределу по I, получаем:

>/шН

(()

. (2.4.8)

Принимая во внимание

(2.4.7)

(2.4.8),

получаем доказательство второго

утверждения леммы. А

ГЛАВА

II.

Источники

СООБЩЕНИЙ

Рассмотрим c^=a

ilV

..,a^ фиксированную последовательность, порождён-

ную источником

[A,

p(s)].

Для реализаций такого вида определена вероятность

р(с^).

При этом, вообще говоря, зависимость между буквами распространяет-

ся на произвольную глубину. Это обстоятельство затрудняет применение зако-

на больших чисел.

Введём в рассмотрение следующие величины:

(c^) = p(c

)p(a

/а

)р(а

4з

)...p(a^ /а^), (2.4.9)

) = p(c

)p(a

/а

а^)р(а

)...p(a^ /а^а^_

q^i(Cf)

= p(c

)p(a^

/а,^,...,^),

яДс^) = р(с

Величины

Чш(^) = Р(

т) nP<

ik-l'-'

ik-ra) (^

^) (2.4.10)

к=т+1

при фиксированном т представляют вероятностное распределение на С

Лемма 4.2. Для дискретного стационарного эргодического источника,

при произвольном m ^

имеет место:

//m%q

(c,)

= -H

(m+I)

. (2.4.11)

Доказательство. Прологарифмируем (2.4.10):

log q

(c^) = /c?gp(c

]£/0gp(a

...,a

). (2.4.12)

k=m+l

Функция togp(a

ik t

). определённая на случайных реализа-

циях c

m+1

, является суммируемой случайной величиной. Так как математи-

ческое ожидание её равно

P(»l

v~,a

) log p(a

/а^

..,a

н(т+1> <0

то к функции /ogp(a

а|

кч

,...,а

1к

)

применима теорема Биркгофа, соглас-

но которой

^PK

ik-l-'

ik-m)

(

mv..a

) (2.4.13)

k=m+l

почти всюду. Разделим (2.4.12) на £ и устремим £ к бесконечности. Первое

слагаемое в полученном выражении с ростом £ может быть сделано меньше